基于Sobol法的宁夏固海扬水灌区ET0敏感性分析

叶 威，伍昊洋，邹全程，赵 璐,2，崔宁博，梁 川

(1.四川大学水利水电学院，成都 610065 ；2 农业部旱作节水农业重点开放实验室，北京 100081)

0 引 言

潜在蒸散发(ET0)是水文循环研究的重要参数，ET0、降水和径流一起决定一个地区的水分平衡，在研究区域水循环中占有重要的地位。ET0也是农业水资源评价、水量平衡模型运行和实际蒸散发估算中必不可少的重要参量，它独立于作物类型、生长阶段和作物管理方式，主要受气象因子影响，因此，计算ET0对单个气象因子或多个气象因子变化的敏感系数[1-3]，可以定量的反应主要气象因子变化和ET0之间的关系。根据ET0对主要气象因子的敏感性系数，可以快速估算当某个气象因子(一阶敏感性系数)或多个气象因子(总敏感性系数)发生变化时ET0的相应变化量。量化各种气象因子的变化对ET0的影响，对于各个地区灌溉制度的制定和水循环的研究具有重要意义。

国内外许多学者常采用敏感曲线法进行ET0的敏感性分析，即把因变量变化与自变量变化的比值绘成曲线来描述敏感系数的特征。侯兰功[4]等人利用此方法对额济纳绿洲进行分析，得出太阳辐射为ET0最为敏感的气象因子。也有学者采用敏感系数法，曹雯[5]等人利用此法对西北地区ET0的各因子敏感性进行分析，发现了太阳辐射是ET0最为敏感的气象因子，这一结果与其他学者对我国长江流域、松嫩平原西部和东北地区进行研究所得的结果不同[6-8]，由此得出不同地区ET0的变化具有不同的控制因子。Sobol全局敏感性方法是进行敏感性分析的一种常用方法[9,10]，可以分析各气象因子的独立敏感性和总敏感性，这是其他敏感性分析方法无法实现的，在各个领域得到了广泛的应用，然而，此法却极少应用到ET0的敏感性分析，仅有泮苏莉[11]等人利用Sobol全局敏感性系数分析方法对嵊泗列岛进行分析，得到了海岛地区ET0对各个气象因子的敏感性系数。此外，关于宁夏固海扬水灌区ET0对各气象因子的敏感性分析也未见报道。基于上，本文拟采用Sobol[11-14]全局敏感性方法分析宁夏固海扬水灌区ET0对主要气象因子的敏感性，得到ET0对每个气象因子的一阶敏感性系数和总敏感性系数。

1 研究区域概况

自20世纪70年代以来，为逐步解决宁夏回族自治区中部干旱带日趋严重的干旱缺水状况，兴建了红寺堡、固海、固海扩灌和盐环定等扬水工程。该区域属于中温带干旱区，太阳辐射强，大陆性气候明显，干旱少雨且强烈蒸发。

宁夏固海扬水灌区(东经105°26′24″～106°14′24″，北纬36°26′24″～37°33′30″)位于清水河河谷平原下游，为研究固海扬水灌区ET0对各气象因子的敏感性，本文拟采用同心站1961-2016年逐日的气象数据(来自中国气象数据共享网https:∥data.cma.cn/)，利用Penman-Monteith方法计算ET0，采用Sobol全局敏感性分析法定量分析ET0对各气象因子的敏感性，对比兴建扬水工程前后各气象因子敏感系数的变化。

2 研究方法

2.1 FAO Penman-Monteith方法[15-17]

(1)

式中：ET0为潜在蒸散发，mm/d；Rn为净辐射，MJ/(m2·d)；G为土壤热通量, MJ/(m2·d)；G相对于Rn取值很小，在计算步长大于等于1 d的情况下，可以忽略为0；T为2 m处日平均气温，℃；U2为2 m处的风速，m/s；es为饱和水汽压，kPa；ea为实际水汽压，kPa；es-ea为饱和水气压差，kPa；Δ为水汽压曲线斜率，kPa/℃；γ为湿度计算常数，kPa/℃。

2.2 Mann-Kendall趋势检验[18-20]

Mann-Kendall方法是基于秩序的非参数方法，被国内外学者广泛应用于分析降水、气温和ET0等因子时间序列的趋势变化。本文选取Mann-Kendall方法对宁夏扬水灌区1961-2016年各气象因子和ET0时间序列进行趋势分析，并检验ET0在这56年间的突变。

2.3 Sobol全局敏感分析法

Sobol方法是基于方差分配的全局敏感性分析方法，原理大致如下：模型函数可以分解为单个变量与单个变量之间相互结合的函数，公式(2)中的方差由近似蒙特卡洛数值积分进行估算。

(2)

式中：D为模型的总方差；Di为变量Xi通过变量Xi作用所贡献的方差；Di,j为变量Xi通过变量Xi，Xj所贡献的方差；Di,j,…,n为变量Xi通过变量Xi,j,…,n所贡献的方差。

定义变量及变量相互作用的方差与总方差的比值为敏感性指数，反映变量Xi对模型输出总方差的直接贡献率,即变量Xi一阶敏感性指数Si可表示如下：

(3)

同理，变量Xi的二阶敏感性系数可表示为：

(4)

变量Xi的总敏感性指数即为各阶敏感性指数之和，表示如下：

STi=Si+Si,j+…+Si,j,…,n

(5)

Si体现的是某一输入参数在输出方差上的影响，而STi体现的是输入参数i的方差的总贡献，包括它的一阶和更高阶方差。公式(3)用于计算一阶敏感性系数，代表ET0对各气象因子的敏感性，公式(5)用于计算总敏感性系数，代表ET0对各气象因子的总敏感性。

3 结果分析

3.1 Mann-Kendall检验结果

根据Penman-Monteith公式计算ET0并利用Mann-Kendall趋势检验法检测其在1961-2016年的突变，结果如图1中所示。

图1 ET0突变检验图Fig.1 ET0 mutation test chart

其中，实线为顺序变化曲线UFk、虚线表示逆序变化曲线UBk，2条临界线±1.96(显著性水平为0.05)。由图1可知，两条序列曲线的交点，大致位于1980年，因此，1980年为ET0在1961-2016年这56年间的突变年。 宁夏固海扬水灌区是20世纪70年代以来发展的大型灌区，通过该灌区的修建，引入大量的黄河水，局部的水循环有一定的变化，对ET0有一定的影响，故1980年作为ET0的突变年具有一定的合理性。

根据突变点检验的结果，本文将平均气温、最高气温、最低气温、相对湿度、日照时数、风速以及ET0分为1961-1980年、1981-2016年和1961-2016年三个时间段分别进行时间趋势分析，分析结果见表1。

表1 气象因子趋势分析结果Tab.1 Meteorological factor trend analysis results

注：Z>0时各因素变化趋势上升，Z<0时为下降， *表示显著，**表示极显著，下同。

由表1可知：宁夏固海扬水灌区ET0在1961-1980年呈下降趋势，1981-2016年呈显著的上升趋势， 1961-2016年呈上升趋势；平均气温、最高气温和最低气温三个时间段均呈上升趋势，1961-2016年呈极显著的上升趋势；相对湿度在1961-1980年呈下降趋势，1981-2016年呈显著上升趋势，1961-2016年呈上升趋势；风速在1961-1980年呈极显著的下降趋势，1981-2016年呈极显著的上升趋势，1961-2016年呈上升趋势；仅日照时数在1961-2016年呈显著的下降趋势。综上所述，1981-2016年各气象因子和ET0较1961-1980年都有上升趋势；1961-2016年除日照时数呈下降趋势，其余气象因子和ET0均呈上升趋势。

3.2 一阶和总敏感系数年内变化结果

利用Sobol全局敏感性分析方法分别计算1961-1980年和1981-2016年两个时间段年内的一阶和总敏感性系数，图2为1961-1980年一阶和总敏感性系数年内变化，图3为1981-2016年一阶和总敏感性系数年内变化。

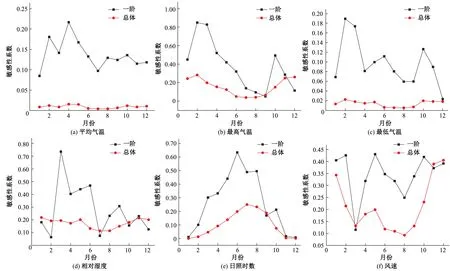
图3 1981-2016年各气象因子一阶和总敏感性系数年内变化Fig.3 Changes in the first-order and total sensitivity coefficients of various meteorological factors from 1981 to 2016

由图2、图3可知，各气象因子的总敏感性系数大体上小于一阶敏感性系数，其中，也有个别月份出现总敏感性系数大于一阶敏感性系数的情况，如：1961-1980年风速的总敏感性系数在1-3月和9-12月均大于一阶敏感性系数。1961-1980年和1981-2016年两个时间段各气象因子的总敏感性系数的年内变化大致呈相同的变化趋势。平均气温、最低气温和相对湿度的总敏感性系数年内近似呈一条水平线，前两者敏感性系数较小，约为0.02，相对湿度的敏感性系数较大，约为0.2。最高气温和风速在年内的变化呈波谷型，年内敏感性系数的最小值一般出现在8月左右，而最大值一般出现在12月左右。1961-1980年和1981-2016年两个时间段，最高气温的总敏感性系数最大值分别为0.26和0.28，最小值分别为0.04和0.039，风速的总敏感性系数最大值分别为0.43和0.40，最小值分别为0.093和0.092。1961-1980年和1981-2016年日照时数总敏感性系数在年内的变化呈波峰型，其中最大值一般出现在7月左右，分别为0.20和0.25，最小值一般出现在12月左右，近似为0。总的说来，总敏感性系数的大小排序为风速>相对湿度>最高气温>日照时数>最低气温>平均气温。

各气象因子的一阶敏感性系数在年内呈多样性和不确定性变化的特点，平均气温和日照时数的一阶敏感性系数在年内的变化大致为波峰型，最小值均大致出现在1月左右，平均气温的最大值出现在4月左右，日照时数出现在7月左右。两个时间段，平均气温的一阶敏感性系数最大值分别为0.26和0.21，最小值分别为0.01和0.08；日照时数的一阶敏感性系数最大值分别为0.55和0.63，最小值分别为0.006和0.008。最低气温、最高气温、相对湿度和风速的一阶敏感性系数年内呈峰谷交替变化的特点，以1961-1980年最高气温的一阶敏感性系数为例，其极大值分别在4月和11月出现，分别为0.32和0.37，极小值分别在3月和6月出现，分别为0.15和0.004。总的说来，一阶敏感性系数的大小排序为相对湿度>日照时数>最高气温>风速>平均气温>最低气温。

3.3 1961-2016年敏感性年际变化

由图2和图3可知，1961-1980年和1981-2016年两个时间段，总敏感性系数年内呈现基本相同的变化特点，而一阶敏感性系数在两个时间段呈不同的变化特点，其大小有明显差异，为探究这种差别，对各气象因子的一阶敏感性系数在1961-2016年的变化进行了趋势分析，计算结果如表2和表3。由表2可知，一阶敏感性系数相对湿度最大，最低气温最小，三个时间段，最高气温和相对湿度的变化量较大，日照时数和风速次之，平均气温和最低气温较小。表3根据Mann-Kendall趋势检验法的结果，更准确的反映了各气象因子在三个时间段的变化趋势。1961-1980年平均气温和相对湿度的一阶敏感性系数呈上升趋势，最高气温、最低气温、日照时数和风速的一阶敏感性系数呈下降趋势。1981-2016年平均气温基本无变化，风速的一阶敏感性系数呈上升趋势，最高气温、最低气温、相对湿度和日照时数呈下降趋势。1961-2016年，平均气温、最高气温、最低气温和相对湿度的一阶敏感性系数呈现下降的趋势，日照时数的一阶敏感性系数呈显著的下降趋势，风速的一阶敏感性系数呈上升趋势。

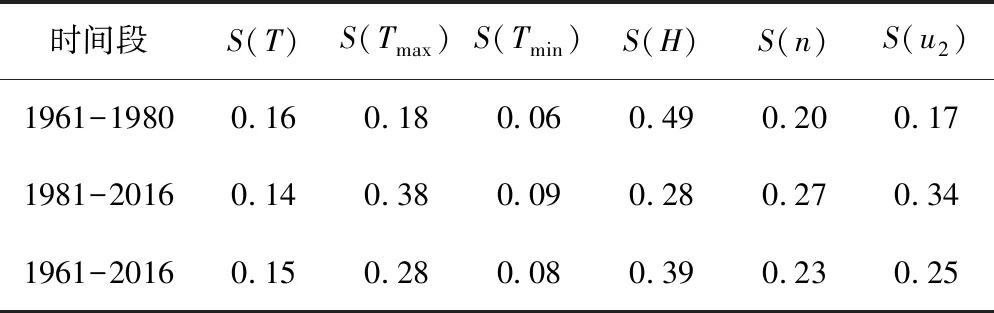
表2 一阶敏感性系数平均值Tab.2 Average value of first-order sensitivity coefficient

表3 一阶敏感性系数趋势分析结果Tab.3 First-order sensitivity coefficient trend analysis results

4 结 语

根据宁夏固海扬水灌区1961-2016年同心站的逐日气象数据，计算该地区的ET0，利用Sobol全局敏感性分析方法计算ET0对各气象因子的一阶和总敏感性系数，并利用Mann- Kendall趋势检验探究ET0和各气象因子的敏感性趋势变化，得出主要结论如下。

(1)各气象因子的总敏感性系数在年内基本上小于一阶敏感性系数，个别月份例外。各因子的总敏感性系数年内呈直线型(平均气温、最低气温和相对湿度)、波谷型(最高气温和风速)和波峰型(日照时数)三种变化特点，而一阶敏感性系数呈不确定性和多样性变化的特点。

(2)1981-2016年各气象因子和ET0较1961-2016年都有上升趋势，1961-2016年除日照时数外的气象因子和ET0均呈上升趋势，日照时数呈下降趋势。1961-2016年，平均气温、最高气温、最低气温和相对湿度的一阶敏感性系数呈现下降的趋势，日照时数的一阶敏感性系数呈显著的下降趋势，风速的一阶敏感性系数呈上升趋势。

(3)本文利用Mann-Kendall检验出1980年为ET0突变年，并将1961-1980年和1981-2016年进行对比，探究宁夏固海扬水灌区的修建对ET0、各气象因子以及ET0对各气象因子的敏感性的变化趋势的影响。根据计算结果可以看出， 1981-2016年各气象因子和ET0均有上升的趋势，ET0对各气象因子的一阶敏感性系数中，风速的一阶敏感性系数呈上升趋势，而平均气温、最高气温、最低气温、相对湿度和日照时数的一阶敏感性系数呈下降趋势。这些变化特点表明大型灌区的修建在一定程度上可以影响ET0、各气象因子以及ET0对各气象因子的敏感性，ET0呈上升趋势说明人工引黄河水对灌区的水分平衡起到一定的调节作用。此外，本文仅基于有限的气象数据分析了ET0、各气象因子和ET0对各气象因子的敏感性，具有一定局限性。

□