基于SIFT与K-means聚类的多源图像匹配算法

文永革

(绵阳师范学院信息工程学院，四川绵阳 621000)

0 引言

数字图像匹配是计算机图像信息处理领域的重要技术，在多源图像的3D重构、立体匹配和运动跟踪等应用领域中得到广泛深入的研究.目前，基于图像特征的匹配方法仍是计算机视觉及相关领域的研究热点，重心在对图像中点、线、区域等图像显著特征的提取，获得图像间较高的匹配度[1].近年来，业界对图像的局部特征描述符进行了大量的研究，其中，加拿大教授Lowe提出的SIFT局部特征提取算法[2]得到了业界重点关注，通过构建128维特征描述子，和多次迭代运算提取图像特征点，虽然SIFT算法已广泛应用在多个领域，但其计算量大、效率不高，文献[3]对SIFT描述子作了一定的改进，降低了特征向量的维数，使得算法的复杂度得到了降低，文献[4]提出一种基于分块匹配的新型SIFT匹配算法，核心在于对图像块的切分和重叠区域的计算，通过剔除非重叠区域来降低特征提取和匹配的时间损耗，文献[5]提出了一种基于 RANSAC的SIFT匹配优化，采用加权的圆形邻域替代原有 SIFT 描述子矩形邻域，并以最优匹配点作为RANSAC 算法初始样本数据集，进一步提纯特征点，文献[6]提出了一种基于SIFT、K-Means 和LDA的图像检索算法，对图像库中图片按其本身特征进行自动分类，有效提高图像检索效率.针对计算效率，文献[7]采用CPU与GPU协同方式对SIFT算法进行加速，但是由于较大图像在GPU内存中的传输速度的限制，算法对于较大图像的计算速度提升并没有得到理想的效果.本文在SIFT算法的基础上结合了K-means聚类算法，通过亚像素插值提升特征点坐标精确度，在此基础上设计辐射模型排除强噪声等不良点以获得稳定的聚类中心，对特征点的选取与匹配进行了进一步优化，又保持了SIFT良好的旋转不变性与尺度不变性， 通过实验仿真，本文算法对不同分辨率、不同尺度图像的匹配精度有较稳定的提升.

1 SIFT 算法

灰度图像中像素点的灰度分布特征与二维高斯模型相似，中心处最亮，离中心越远亮度随之降低，因此本文中的图像灰度分布特征，用优化的高斯模型代之描述.SIFT算法正是通过用不同尺度的高斯函数对图像进行平滑处理，比较平滑后图像的差别，差别大的像素就是局部范围内的极值点，根据这些点的邻域采样求得特征向量，提取这些点的位置、尺度、旋转不变量.SIFT算法对旋转、尺度缩放、亮度变化保持不变性，对视角变化、仿射变换、噪声也保持一定程度的稳定性[2]，经优化的匹配算法适用于海量特征数据快速、准确的匹配，还可以满足一定程度的实时性要求.

1.1 SIFT 特征检测

(1) 尺度空间极值检测

差分尺度空间的极植点检测是通过高斯核与图像的卷积运算实现.图像的尺度空间函数用L(x,y,σ)表示，通过尺度变化的高斯函数G与数字图像I卷积运算，搜索所有尺度上的特征图像位置，因此，一幅二维图像的尺度空间可表示为：

L(x,y,σ)=I(x,y)⊗G(x,y,σ)

(1)

式中(x,y)代表像素点的空间坐标，σ代表采用的尺度参数，σ的大小决定图像的平滑程度，值越大对应图像的粗糙特征，越小对应图像的细节特征.

SIFT算法图像空间中特征点的检测，通过两个相邻高斯尺度空间的图像相减得到高斯差分DoG[8]的响应值图像D(x,y,σ)，其响应值图像表达式如下：

D(x,y,σ)=I(x,y)⊗(G(x,y,kσ)-G(x,y,σ))

(2)

k为两相邻尺度空间倍数的常数.

(2) 特征点的定位

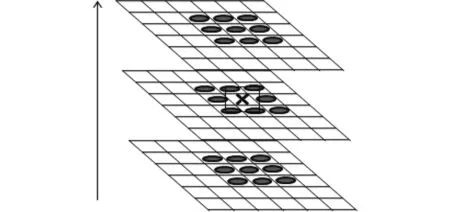
图1 相邻尺度空间极值点比较示意图Fig.1 Comparison of Extremum Points in Adjacent Scale Spaces

图像特征点的定位是通过对图像D(x,y,σ)进行局部极值搜索来实现，在位置空间和尺度空间中定位特征点.如下图所示，为了实现查找尺度空间的极值点，需要每一个采样点与它同尺度8个相邻点和两相邻尺度空间的18个相邻点进行大小比较，如一个点在上述空间是最大或最小值，则认为该点是图像在该尺度的一个特征点，移动滑动模板，直到完成对尺度空间中每个像素的最大最小值比较.

(3)特征点的方向

计算特征点幅值大小，并根据极值点邻域像素的梯度方向分布特性，为每个极值点指定方向参数，使算子具备尺度和旋转不变性.

(3)

(4)

a(x,y)为极值点处梯度的模值，θ(x,y)为此特征点的梯度方向，L为(x,y)点所在的尺度.在此，图像的关键点已检测结束，且其位置、方向、尺度三个特征值已确定.

(4)特征点的描述

通过以上步骤，每个特征点都具有位置、尺度和方向三种属性，将特征点相邻点分成4×4个子区域，每个子区域包含一个种子点，每个种子点通过高斯加权后以45°角为度确定8个梯度方向，箭头的方向代表了特征点梯度方向，箭头长度代表该点的幅值大小，用一组向量来描述，该描述子使用128维信息来表达尺度空间的SIFT特征向量.

2 K-means聚类算法

针对SIFT特征点优化问题，根据关键点特征向量的欧式距离，运用K-means聚类算法对SIFT特征向量进行聚类，选取与整体差异最小的特征向量作为初始聚类中心，据此实现特征向量匹配可大大降低计算维度.

2.1 K-means 算法

是一种迭代聚类算法，其算法思想是对大量样本数据进行抚今迭代计算，按样本间的欧式距离大小归类成k个簇，每个簇内数据间聚集更紧，簇间的距离尽量变大.算法快速、简单, 其时间复杂度O(ntk)近于线性，正比于数据集中对象的数量n、算法迭代的次数t和簇的数目k，对于处理大数据集计算有较高的效率.

2.2 K-MEANS 算法基本流程

(1)从n个数据对象S=x1,x2,x3…xn，任意选择k个对象μ1, μ2…μk作为初始聚类中心；

(2)算法采用误差平方和准则函数作为聚类准则函数，根据每个聚类对象的均值求得中心对象，计算每个对象与所有中心对象的距离；并根据最小距离将相应对象归入距离最近的中心对象的类中.

(5)

(3)重新计算每个聚类Cj的均值uj，确定该聚类的中心对象；

(6)

(4)重复(2)(3)步直到每个聚类中心变化小于阈值为止.

3 SIFT 特征点优化和辐射聚类模型

SIFT特征点初步定位的坐标值一般采用整数值，并非特征点精确坐标，这在相机标定、图像匹配、图像融合以及三维重构等应用中，计算图像间距离和像素距聚类中心距离时会产生较大误差，导致聚类中心不稳定和局部优化.为了进一步减小图像特征点计算、匹配时的误差，文中采用亚像素插值算法对特征点进行精确定位，采用优化辐射模型进一步排出噪声等异常点的影响，提高中心精确度和减小计算量.

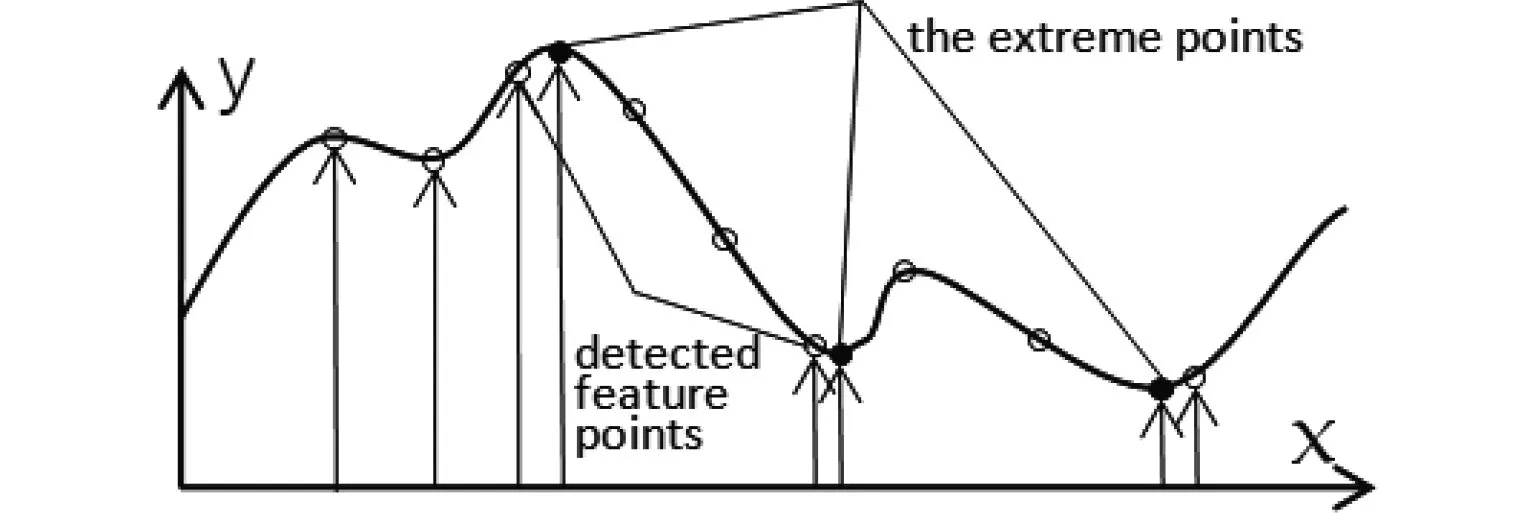
图2 离散空间和连续空间的极值点Fig.2 Extremum Points of Discrete Space and Continuous Space

3.1 亚像素插值法sub-pixel interpolation(特征点的精确定位)

传统SIFT算法结合Harris角点算法对特征点进行筛选，对筛选结果中的不良点排除未达最优化，其特征点结果可能是离散空间中的局部极值点，如不能正确排除，特征点的选择误差会严重影响后续聚类中心的计算和特征点的匹配[9].为了进一步准确定位sift特征点，在前期研究基础上，本文对离散空间的极值点进行三维亚像素插值，以提高图像分辨率以弥补成像设备不足，得到连续空间中更准确的极值点的位置，如图2所示.

对式(2)有，根据泰勒展开式有：

(7)

式中D(X)即为D(x,y,σ)，X=(x,y,σ)T.

(8)

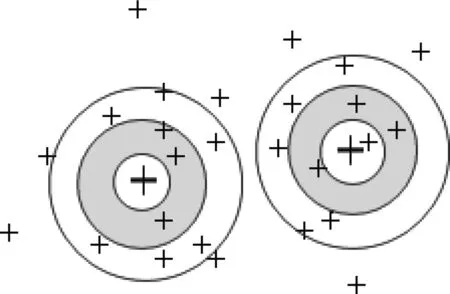
图3 辐射模型示意图Fig.3 Diagram of Radiation Model

4.2 辐射模型分析

文中采用Euclidean度量方法计算空间像素点距离，算法要求每一个数据点参与均值计算，故均值的计算结果对噪声和孤立点较为敏感，少量的异常点会对平均值产生较大的影响，导致聚类中心的计算出现较大误差.本文在反复实践的基础上提出了一种搜寻聚类对象的辐射模型，从聚类中心以不同步长向外辐射，找到辐射范围内特征相近的点，直到聚类的最外环相切，这类特征点在更大程度上具有内容关联性[10]，对于其余未归并入某一聚类的特征点，再根据其距聚类中心的距离远近归并到相应聚类中.在程序实现中定义了辐射步长：radioStep=meanRange*radio*step，通过逐次调整不同的step步长来限制辐射的精度，调整筛选的粒度，其中步长step代表两个圆的径向长度变化值.

辐射模型算法实现了两点：第一，保证了并入聚类中的点是正确的.第二，对于少量未归并入聚类的点，根据相似性原理进行归并，大大减少了计算量，同时，也保证了该点归并入聚类的正确性.因此，辐射模型算法保证每一个点的分类正确，减少计算量，克服异常点对聚类中心计算产生的影响，从而提升聚类计算的正确率.

5 实验结果分析

5.1 旋转不变性与尺度不变性实验

为了验证本文算法在旋转不变性与尺度不变性上保留了良好特性，文中使用几幅经典的数字图像作为实验图像，将对比图像中的一张进行0～180度的旋转，并使用本文算法对旋转前后的图像进行匹配，如图4所示，并将对比图像中一张进行尺度大小变化，对比示意图如图5，记录每次匹配的结果与匹配正确率.

图4 旋转不变性匹配示意图Fig.4 Schematic Diagram of Matching Rotation-invariant

图5 尺度不变性匹配示意图Fig.5 Schematic Diagram of Scale-invariant

通过匹配结果可以看出，本文算法对旋转前后、缩放前后的图像进行特征点匹配时，特征点匹配准确度并未发生变化，可见，算法保持了良好的旋转不变性与尺度不变性.

5.2 特征点匹配精度实验

本组实验采用的是相同景物的不同视角图像，以第一张为基准图，与第二张进行匹配，并与给定的特征点参考表进行比对，得到匹配正确率.优化前后算法执行结果如表1和图6所示:

从本组对比实验可得，本文算法处理结果减少了原有SIFT点匹配中的多处错误匹配，是由于K-means聚类结合了图像自身内容的判断，提高了特征点的定位精度，提供了准确实现数据对象聚类的优化条件，实现图像特征点的提取正确率，较好地克服了原有SIFT特征点计算局部最优的不足.

图6 SIFT算法(上)与本文算法(下)匹配精度对比Fig.6 Comparison of Matching Accuracy between SIFT Algorithm (above) and Algorithm in this Paper (below)

6 结束语

本文针对原始的SIFT特征点匹配算法进行了对匹配特征点数量与精度的优化，提出了一种结合K-means的SIFT特征匹配算法.首先对SIFT特征点进行聚类分析，为克服SIFT特征点坐标取整带来的欠准确，使用亚像素插值算法搜索更精确的特征点位置，进一步通过辐射模型优化聚类来剔除强噪声点和孤立点，从而提高特征点匹配的精确度和正确率.实验结果表明，本文算法在保证图像特征点匹配的旋转不变性与尺度不变性的前提下，通过提高图像特征点的定位精度，剔除不良点提升特征点正确率，实现了多视角图像的精确匹配，算法实现的时间复杂度研究未在本文过多涉及.