闸门调度对下游河岸冲刷影响规律的研究方法探讨

肖小玲，沈家文

(1. 福建华电金湖电力有限公司，福建 将乐 353300；2. 武汉大学水利水电学院，湖北 武汉 430072)

水力调控是工程上实现电站下游防治冲刷的有效手段，一般采用闸门调度的方式来完成[1]。此前已有很多学者对电站下游冲刷进行了研究，如下游冲刷引起的河床演变趋势以及河势的走向等问题。其主要的研究内容是分析河道水流结构形态对边坡稳定的影响规律[2-3]。为了得到科学精准的闸门调度方案，可通过原型资料分析[4]、物理模型观测[5]和数学模型计算[6]等三种方法进行研究。但是原型资料的收集难度较大，且资料范围具有局限性，不能完全依托资料高效快速地分析得到闸门调度方案；而物理模型和数学模型都是由于其模拟的复杂性导致不能灵活地进行闸门调度试验。通过调查发现，人工神经网络模型在闸门调度的水文方面已经开展了研究[7]，但讨论闸门调度对下游河岸冲刷影响的研究还不是很多。

因此，本文基于物理模型试验，观测不同洪水频率工况时不同闸门调度方案下电站下游河道水流动力条件与边坡冲刷影响的对应关系，讨论如何通过神经网络高效快速地分析研究闸门调度中影响下泄流量的各因素对下游河道内水流动力条件改变程度的敏感性，进而得到闸门调度对边坡冲刷的影响规律，这对高唐电站闸门调度运行管理具有科学的指导意义。

1 研究区域与资料

高唐水电站位于福建省西北部的将乐县高唐镇上游约2.5 km处，为闽江上游金溪流域梯级开发的第七级电站。水电站采用河床径流式，以发电为主。坝址以上流域面积6 683 km2，流域内雨量充沛，多年平均降雨量1 684 mm，多年平均来水量68.43亿m3，多年平均流量217 m3/s，水库正常高水位146.00 m，对应库容2 144万m3，是一个日调节水库。泄水闸坝段布置在主河床的中部，泄水闸坝长172 m，闸坝高程153 m，共9孔，溢流堰顶高程134 m，孔口尺寸：15 m×12 m(宽×高)，驼峰式溢流堰，采用弧形钢闸门挡水。闸后采用底流和戽流相结合的消能方式，中间4孔闸(4～7号孔)采用底流消能，闸后设37 m长的消力池，两端剩余的5孔闸为戽流消能，在闸后设钢筋混凝土短护坦，长15 m。电站枢纽平面布置见图1。

图1 高唐水库电站枢纽平面布置示意图

由于大坝左岸下游河岸建设期未设置防护工程，2007年投产以来，每年洪水季节，当大坝下泄洪水重现期超过五年一遇时，左岸岸坡均有不同程度的冲刷，岸坡坡脚不断后退。为了减小高唐水电站下游左岸边坡崩岸所产生的负面影响，需要通过简易方便的数学模型来分析库区来流、闸门调度方式与电站下游河岸水动力条件之间的对应关系，研究合理的水电站闸门开启方式和调度方案，调控电站闸门下泄水流流态，实现下泄水流消能效果最佳，以期改变电站下游左岸冲刷河段内水流结构。

2 研究方法

2.1 数学模型方法

高唐水电站泄洪闸孔数较多，理论上闸门开启组合形式复杂，物理模型试验难以全部模拟闸门调度组合。因此需要建立一个可以实现闸门调度对下游河道水力条件变化控制影响的耦合数学模型。本文拟准备选择通过改变下游水力条件(流量、水流结构和流速等)，动态调整一般水动力模型中纵向和横向分速度的数值。采用试验监测与多方法估算相结合的手段，增加模型参数的确定性以及对不同水力条件的自适应能力。

2.1.1 闸门调度与流量的响应模型

为了比较具体化地定量研究闸门调度对水量的调配和电站下泄水流流量的影响，本文拟采用3层BP(back-propagation)神经网络模型[8]对闸门调度与电站下泄流量之间进行多元关系拟合。其拟合计算结构示意图如图2所示。

图2 人工神经网络拟合计算结构示意图

由图2可知，在拟合计算结构中输入层共4个神经元，分别为库区坝前水位、开闸孔数、闸门开度和开闸排列，而输出层为闸门下泄流量。本文中人工神经网络模型中样本的划分及训练方法采用提前终止法[9]，其训练样本为高唐水电站物理模型试验观测的资料结果，其可靠性良好。对神经网络模型结果处理采用归一化三维空间内的曲面观测分析方法，通过观测曲面上坝前水位、开闸孔数、闸门开度和开闸排列等4个变量对闸门下游下泄流量之间的相应关系，可以得到各影响因素与下泄流量的相关性明显程度，进一步得到闸门频繁调度工况下调控下泄流量的变化特性。

2.1.2 流量与河岸冲刷速度的响应模型

在不考虑电站闸门调度以及消力池消能防冲的影响后，从不影响末端开始可以认为横断面为自然河道断面。虽然河道水力半径会随着下泄流量不同而变化，但通过水文观测，在同一河道断面中其平均流速大小与下泄流量一般会呈对应关系。在本文通过物理模型试验观测坝后50 m的同一断面，其观测断面和观测点如图3所示。

图3 物理模型试验中流速观测断面及观测点位布置图

监测断面上布置4个流速监测点，采用ADV测量各监测点的三维流速。不同的坝前水位、开闸孔数、闸门开度和开闸排列会导致监测点位上流速发生变化。根据水力学及河流动力学知识，可认为坝下游左岸冲刷速度主要受到水力直接冲击的直接影响，而冲刷速度矢量主要由速度矢量在垂直于左岸方向的速度分量和速度矢量向左岸的偏移角度共同决定。各监测点位流速作用示意图如图4所示。

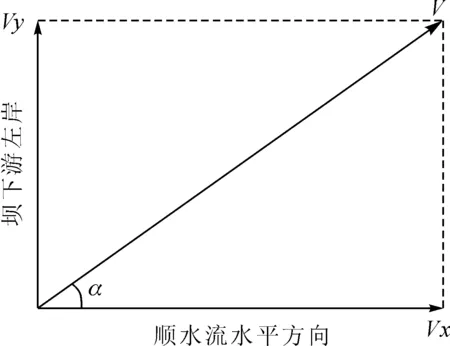
图4 坝下游左岸冲刷速度作用示意图

定义坝下游左岸冲刷速度的贡献U为

(1)

式中：Vxi和Vyi分别代表第i个监测点位上水平面中顺水流水平方向的速度分量大小、指向坝下游左岸方向的速度分量大小；N为监测点位的个数。

在具有其独立的自然属性的河道上，不同的坝前水位、开闸孔数、闸门开度和开闸排列所决定的下泄流量，必将与下游冲刷速度V是一一对应关系。因此，就可以建立流量与河岸冲刷速度的贡献响应数学模型。

2.2 模型敏感性分析方法

现阶段在诸多数学分析领域都采用敏感性分析方法来研究和预测数学模型中具有属性的输入层在可能取值范围内变动对输出层数值的影响程度。通过研究数学模型属性的敏感性系数的大小来分析输入变量对输出变量的重要性。其内容核心为考虑合理存在的属性敏感性系数，计算并对各属性敏感性系数排序，通过排序结果分析各属性的重要程度。而敏感性分析又分为局部敏感性分析和全局敏感性分析。其中全局敏感性分析可以分析数学模型中所有属性对模型输出的影响，以及各属性之间的彼此作用对模型输出的影响。

因此，建立闸门调度与下游冲刷的响应神经网络数学模型后，评价电站闸门调度对下游冲刷的影响，可进一步对该模型的参数进行全局敏感性分析。目前常见的全局敏感性分析方法，主要分为PAD2法[10]、EFAST法、Sobol法[11]以及基于ANN的权值分析法[12]等。

2.2.1 敏感性分析方法的选择

通过统计现阶段对数学模型全局敏感性分析方法，可以分析得到各种方法的优劣。将四种全局敏感性分析方法进行对比，可得到表1所示的统计成果。

由表1可知，对于数学模型的全局敏感性分析方法最优选择Sobol法，这也是目前最常用的使用方法，已经被广泛地运用于经济、医药、生物、环境以及社会学等各大领域的数学模型分析中。但是由于该方法计算量较大，所以针对其不足已经有人研究出了Sobol法的改进算法，以此来解决该方法的不足。因此，在本文中建议采用Sobol法的改进算法来分析闸门调度对下游冲刷速度的响应模型的敏感性分析。

但又由于神经网络模型属于黑箱模型，其响应曲面的结构难以确定。模型的敏感性分析结果对分析过程采样量的依赖性很高，所以仅采用Sobol法的改进算法来分析模型的全局敏感性是不够的。因此在本文中需要进一步采用计算方法简单的ANN权值分析法来验证全局敏感性分析结果的可靠性。即在全局敏感性分析的基础上，通过了ANN权值分析法验证的结果才是科学可靠的敏感性成果。而且其计算过程简单，应用十分广泛，所以在本文中建议运用。

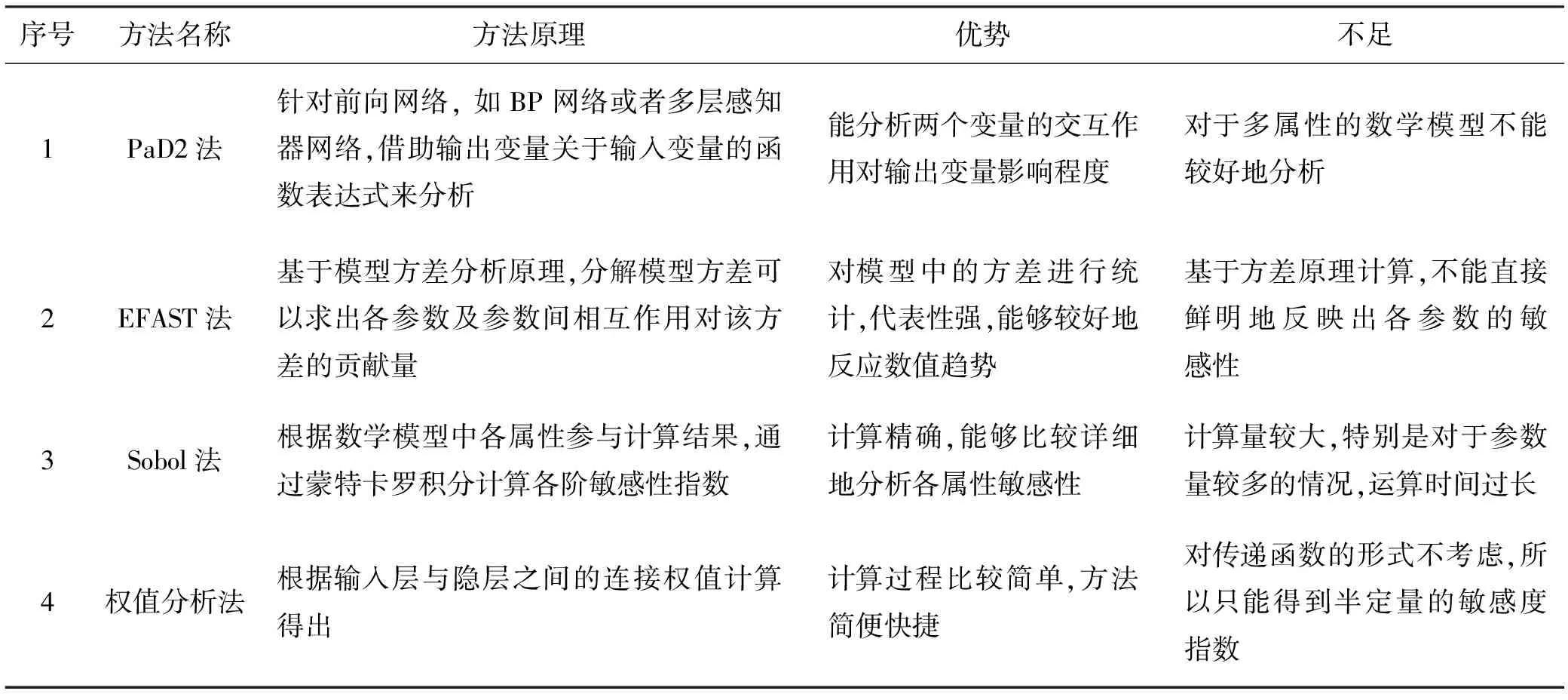
表1 全局敏感性分析方法的对比结果表

2.2.2 敏感性分析的内容

考虑到人工神经网络在数学模型计算中复杂性，首选考察该模型在闸门调度对下游流量方面的敏感性，可通过ANN的权值分析法计算坝前水位、开闸孔数、闸门开度和开闸排列等4个属性变量的相对重要性指数I，将其作为Sobol方法对模型全局敏感性分析成果的验证对象。当4个属性变量的相对重要性指数I在两种方法中的结果一致时，那么全局敏感性分析成果可采纳；而当结果不一致时，那么全局敏感性分析过程中的训练样本需要进一步增加。

再采用Sobol方法对模型各因子对坝下游左岸冲刷速度的影响进行评估。评估过程应该保证采样数量，在计算时间精简的前提下只有采样数量足够多，根据中心极限定理——蒙特卡罗法计算得到的敏感性指数才真实。即在实际数学试验模型分析中，在保证足够的样本数量的前提下，根据各因子分布特征选择合适的样本数对应的敏感性指数成果，该成果在基本稳定状态下才被认为有效。

闸门调度对下游左岸冲刷数学模型的全局敏感性分析的内容表达形式主要包括总敏感性指数和各因子的一阶敏感性指数。其中总敏感性指数是表示数学模型中各因子彼此之间共同作用对下游左岸冲刷过程产生的影响程度，而一阶敏感性指数则是表示单一因子独立对下游左岸冲刷过程的影响程度。敏感性分析结果一般各因子会按照一阶敏感性指数的大小进行大小排序。而根据各因子的敏感性大小，可以进一步分析得到各因子对闸门下游左岸冲刷过程的贡献度，也为分析闸门调度对下游冲刷影响规律提供了科学依据。

3 结 语

本文建议采用人工神经网络建立闸门-流量模型，并结合流量与下游左岸冲刷速度的响应关系，估算高唐电站闸门调度方式对下游左岸冲刷的影响，可评价模型中各参数对下游左岸冲刷过程的敏感度，得到以下结论：

1)基于闸门水流流动过程的物理过程，简化下泄流量与左岸冲刷的对应关系，通过神经网络可以将闸门调度中各种影响因素-下泄流量-下游左岸冲刷速度建立成为一种响应的数学模型；

2)采用Sobol方法与权值分析法一起分析模型的敏感性，既能保证闸门调度对下游左岸冲刷影响模型的敏感性结果可靠，也能通过Sobol方法计算得到各影响因子之间的敏感性相对大小顺序，进而得到各影响因子对坝下游左岸冲刷的作用规律。