一级气体炮内弹道方程修正及仿真验证
熊 镐,王惠源,王玲儒
(1.中北大学 机电工程学院,山西 太原 030051;2.石家庄经济学校,河北 石家庄 050000)
气体炮是一种利用压缩气体作为动力源驱动弹丸运动的发射装置。气体炮相比于传统火炮,在获得较高初速时,弹丸需要承受的加速度和应力较小;发射过程中不存在高温特性,使用寿命长;发射稳定性高,安全可靠。1946年,美国研究成功第一门利用轻质气体作为动力源的一级气体炮[1]。此后,气体炮的研究引起了世界各国的广泛兴趣。
研究人员对气体炮内弹道进行了多方面的研究,赵俊利等[2]分析了影响气体炮内弹道的因素,推导出实用的气体炮内弹道方程,在具体数值计算上进行了简化,该方程在本文中称之为经典方程;赵希欣等[3]应用气体动力学理论及配合间隙的影响建立考虑气体泄漏的内弹道模型;胡静等[4]分析了气体炮不同气体工质的做功能力,并推导了不同工质在真空中自由膨胀获得极限速度的关系式。一级气体炮内弹道计算大多是采用文献[2]中的内弹道方程,通过引入虚拟质量系数的方式计算内弹道过程中的次要功,经火炮内弹道计算的反复验证,内弹道计算中引入虚拟质量系数具有极高的可靠性;Mark Denny在文献[5]中使用一种指数式的气体炮内弹道方程,文献[6]对比了文献[2]与文献[5]的内弹道方程,但并未引入次要功系数,而是直接加上阻力项,并通过实验验证,认为文献[2]中的气体炮内弹道方程具有更高的可靠性;李锋等[1]在文献[2]的内弹道方程的基础上提出一种基于密度的修正方式,对一级气体炮内弹道方程进行修正,并通过仿真验证。
一级气体炮内弹道计算经典方程是在火炮内弹道理论基础上,通过理论分析和推导,获得炮口初速与内弹道过程的解析表达。与火炮不同,气体炮大多有较大的气室容积,经典方程在气室容积较大时出现极大的误差,在实际应用中存在一定的局限性。文献[1]中对炮管内气体密度表达式进行修正,推导了新的气体炮内弹道方程,并进行了仿真验证,该方程在本文中称之为修正方程1。但在实际使用中,修正方程1仍然存在一定的误差。笔者在分析了经典方程和修正方程1的问题及原因的基础上,对虚拟质量系数中的气体动能修正项计算方法进行了修正,并推导了新的气体炮内弹道方程,称之为修正方程2,将之与经典方程、修正方程1以及数值仿真结果对比,完成了对气体炮内弹道方程的修正及验证,证明了修正方程2在气体炮内弹道计算中具有更高的可靠性。
1 气体炮内弹道方程
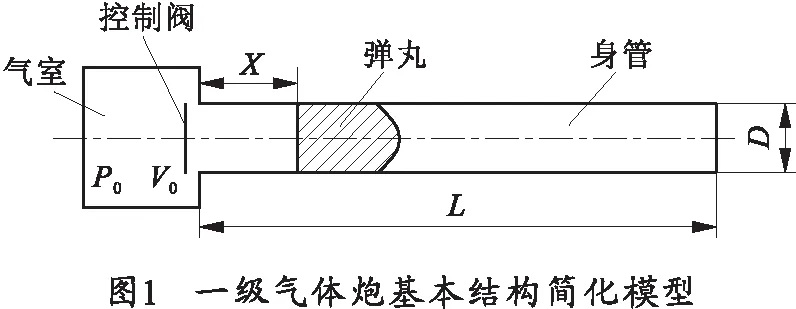
根据一般的一级气体炮结构,建立一级气体炮基本结构简化模型,如图1所示,P0为初始膛压,V0为初始容积,L为身管长度,X为弹丸行程,D为气体炮口径。并有如下基本假设[2-4]:
1)气室气体视为理想气体,整个内弹道过程认为是等熵绝热膨胀过程,温度始终为300 K,即气体绝热指数为常数。
2)不考虑弹前空气阻力的影响,不考虑控制阀对气流的影响。
3)各类能量损失在虚拟质量系数φ中考虑,不存在漏气情况。
4)不考虑后效期气体对弹丸的作用。
1.1 内弹道经典方程分析
基于上述假设,在理想状态内弹道方程的基础上,引入虚拟质量系数φ来计算各类能量损失,通过气体动力学气体绝热方程计算膛内平均压力,积分后得到气体炮经典内弹道方程[2]:
(1)
式中:vm为弹丸初速;k为气体绝热指数;A为身管截面积;m为弹丸质量。
虚拟质量系数φ关系式为
(2)
式中:K为与摩擦力、弹丸旋转等能量损耗有关的次要功系数,由实验测得,此处取1.1;mg为气体质量,式(2)等号右边第2项为气体运动功修正项。
根据理想气体状态方程,气体质量mg为
(3)
式中:μmol为气体摩尔质量;R为气体常数;T为绝对温度。
根据式(1)一级气体炮内弹道经典方程,炮口初速随气室容积变化规律如图2所示。可以看出,气室容积较小时,计算结果与仿真结果基本相符,随着气室容积增大,仿真结果与计算结果的误差逐渐增大;当气室容积增大到一定程度,式(1)计算结果中,炮口初速呈下降趋势,仿真结果炮口初速则随着气室容积增大而增大。对比图2中的弹丸初速,发现初始压力较大时,经典方程的计算结果与数值仿真结果偏差更大,可以认为,经典方程仅适用于气室容积与初始压力较小的一级气体炮的内弹道计算。
1.2 内弹道修正方程1分析
气体炮内弹道修正方程1认为,经典方程中密度ρ定义为气体质量与炮管容积之比,没有考虑气室容积的大小,当气室容积相对于炮管容积较大时,就会导致密度显著增大,导致气体附加质量人为变大,从而出现气室容积越大炮口初速越小的情况[1]。
文献[1]中将气体密度表达式修正为
(4)
则虚拟质量系数φ表达式变为
(5)
气体炮内弹道修正方程1:
(6)
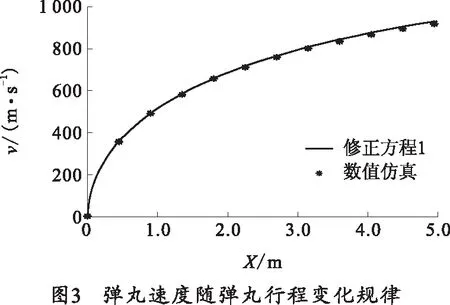
根据式(6)一级气体炮内弹道修正方程1,初始压力P0=20 MPa,初始容积V0=50 L时,弹丸速度随弹丸行程变化规律如图3所示。可以看出,弹丸行程较小时,计算结果与仿真结果基本相符,随着弹丸行程增大,仿真结果与计算结果的误差逐渐增大。
1.3 内弹道修正方程2推导
通过对一级气体炮内弹道经典方程推导过程分析,与数值仿真对比,认为内弹道经典方程忽略了气室容积对膛内气体的影响;内弹道修正方程1虽然考虑了气室容积的影响,但是忽略了气室形状对气体的影响,由气体动力学理论可知,气室直径与身管口径的差异会造成管内气流状况与假设情况有差别。
通过对火炮内弹道分析,气体运动功E表达式为
(7)
式中,vX为该时刻的流速。
根据气体质量均匀分布假设:
(8)
假设气体速度按线性分布:
(9)
将式(8)、(9)带入到式(7)中并积分,得:
(10)
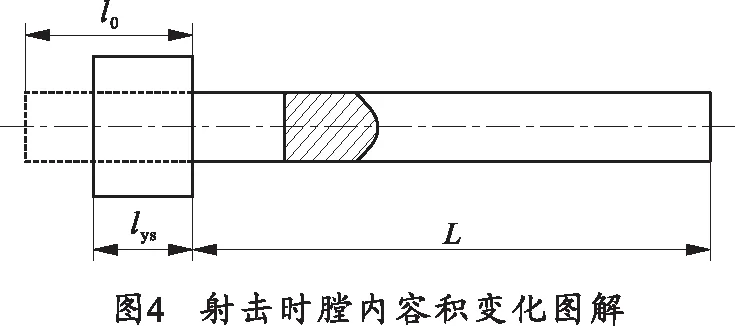
式中,K0即为虚拟质量系数中的气体运动功修正项。在K0的推导中,并未考虑气室截面积和身管截面积的差异,事实上,气体炮往往有较大的气室容积,考虑到气室到身管的缩径情况,K0必须修正。修正方程1针对气体密度的修正方式,考虑到了气室容积的影响,但未考虑气室到身管的缩径情况,所以造成了随着弹丸行程增大,弹丸速度误差越来越大的情况。定义气室扩大系数为χ,弹丸相对行程长为Λ,模型如图4所示[7]。
则:
(11)
(12)
式中:l0为气室缩径长;lys为气室长。则:
(13)
那么,虚拟质量系数φ1的关系式变为
(14)
由式(14)可以看出,新的虚拟质量系数φ1比修正方程1的虚拟质量系数φ增加了有关气室结构的修正项。
根据弹丸运动方程,弹丸的速度为
(15)
式中,P为平均膛压,根据热力学基本方程,平均膛压为
(16)
将式(14)、(16)代入式(15)并积分,则:
(17)
式(17)即为一级气体炮内弹道修正方程2.
2 气体炮内弹道方程对比验证
为了验证修正方程2的可靠性,利用流体仿真软件FLUENT对一级气体炮内弹道过程进行数值仿真,在与理论计算相同假设条件下对不同气体工质(氢气、氦气、空气)在不同气室容积下的弹丸膛内运动过程仿真。仿真过程相关设置如下:
1)仿真采用压力基瞬态求解器,由于气体炮内弹道过程中,气室压力在极短的时间内有极大的变化,缩短时间步长有利于提高弹丸速度计算精度,时间步长设为1 μs,计算总时间为0.01 s,每一步循环次数为30.
2)利用FLUENT动网格技术,采用二维结构化网格,发射过程中膛内流场区域内的网格会随着弹丸运动不断变化,数值仿真过程中应用弹性光顺法和动态分层法相结合的网格更新技术,保证膛内流场的网格质量与计算精度。
3)采用SST 湍流模型,求解控制选用couple算法一阶迎风格式对内弹道过程中膛内流场情况进行计算。
4)编写用户自定义函数(UDF)嵌入到FLUE-NT中,实现读取弹底压力变化情况,并定义阻力项,根据弹底压力变化情况,计算膛内任意时刻弹丸运动情况。
主要仿真参数:弹丸质量m=1 kg;身管截面积A=0.785 dm2;身管长L=5 m.
气室容积V0=50 L,初始压力P0=20 MPa,气体工质为氦气时,弹丸出膛口瞬间膛内压力分布与速度分布如图5~8所示。可以看出,气流从气室到身管,缩径造成气流速度快速增加和压力的快速降低,可见气室形状对膛内流场的影响不容忽视。




在不同气室容积和不同气体工质情况下,3种修正方程以及数值仿真结果对弹丸初速的对比如表1所示。其中容积比r为
(18)
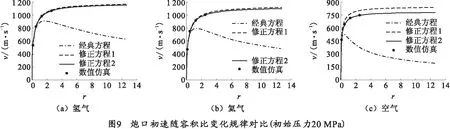
表1、图9、10为经典方程、修正方程1、修正方程2与数值仿真结果在不同气室容积下的计算结果对比。

表1 计算结果对比(L=5 m,P0=20 MPa)
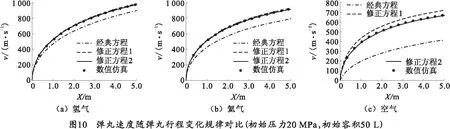
结合图9、10和表1可以看出:
1)当容积比较小时,3种一级气体炮内弹道方程计算出的弹丸初速曲线基本重合,且与数值仿真结果一致;但随着容积比的增大,经典方程出现容积比增大弹丸初速减小的情况,修正方程1与数值仿真结果基本一致,但依旧存在一定的误差,修正方程2则与数值仿真结果始终保持较高的一致性。
2)对比3种不同气体的计算结果,当气体工质为氢气时,修正方程1、修正方程2和数值仿真三者所得结果偏差很小,当气体工质为氦气时,三者所得结果出现了一定的偏差,当气体工质为空气时,三者计算结果出现了极大的偏差。但不论哪一种气体工质,修正方程2所得结果都更接近数值仿真结果。
3)3种内弹道方程计算所得弹丸膛内速度变化规律基本相同,但修正方程2的计算结果与数值仿真的结果更接近。
3 结论
一级气体炮内弹道方程是从火炮内弹道理论中演化而来,火炮的弹膛容积比往往较小,且膛压较大,忽略气室结构尺寸来简化计算不会造成太大误差,因此气体炮内弹道经典方程在容积比较小时,计算结果与实测结果偏差较小,基本可以满足工程设计要求。
与火炮不同,气体炮往往有较大的气室容积,修正方程1和修正方程2都考虑了气室结构对一级气体炮内弹道的影响,进而对内弹道方程进行修正。修正方程1通过对密度表达式进行修正推导出新的气体炮内弹道方程,相比于经典方程,修正方程1考虑了气室容积对气体炮内弹道的影响,具有更广的使用范围和更高的可靠性,但是未考虑从气室到身管的缩径对气流的影响。由于修正项最终作用到虚拟质量系数中的气体运动功修正项上,由气体动力学可知,缩径对气流有加速作用,忽略缩径就造成了气体运动功计算结果小于实际的气体运动功,因此弹丸运动功相应地增加,计算出的弹丸速度也高于实际的弹丸速度,这也就造成了修正方程1在计算分子质量较大的气体工质内弹道时误差较大。修正方程2考虑了气室容积和气室结构对膛内流场的影响,对虚拟质量系数中的气体运动功项进行修正。
修正方程2与经典方程、修正方程1以及数值仿真结果对比表明:在容积比较小时,3种内弹道方程计算结果基本一致;但是在容积比较大时,经典方程计算结果与数值仿真结果出现较大偏差;与数值仿真结果对比,修正方程1相比于修正方程2存在较大误差,且当气体工质分子质量较大时,误差也随之增大,而修正方程2计算结果与数值仿真结果始终表现出较高的一致性,证明了修正方程2的正确性与适用性。

