机械振动系统仿真
(闽江学院物电学院 福建 福州 350108)
机械振动在工程实际和日常生活中普遍存在,为了认识振动现象,有必要研究和掌握振动规律,掌握它的益处来为生产和生活服务,同时在生产和生活中有效的避免振动造成的危害,本文对三自由度机械振动系统进行建模仿真准确直观的获得系统振动情况。
一、建立系统数学模型:
为了便于分析和计算,在满足工程要求的前提下,把实际的振动系统抽象为数学模型[1]。三自由度机械振动系统是相对简单问题,可以直接根据牛顿定律建立系统动力学微分方程[2]。
三自由度机械振动系统如图1所示:
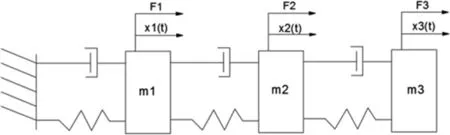
图1 三自由度机械振动系统
该系统的动力学方程如下:
为了简化计算,令质量m1=m2=m3=m,c1=c2=c3=c,k1=k2=k3=k,F1=F2=F3=sin(2t)
写成矩阵的形式如下:
即:
二、构建系统simulink模型及仿真
在现代控制理论中,为了实现对一个动态系统进行完整的描述,将状态方程和输出方程总合起来,构成了系统的状态空间表达式。状态方程具有可分离的数学结构,在求解多变量问题状态空间法有明显的优越性。三自由度机械振动系统是多输入多输出系统,可应用状态空间法在时域内进行求解分析,根据状态方程的解对系统做出评估[3]。本文利用Simulink中的状态空间模块对系统进行建模仿真。
将(5)式转化为状太空间方程[4]:
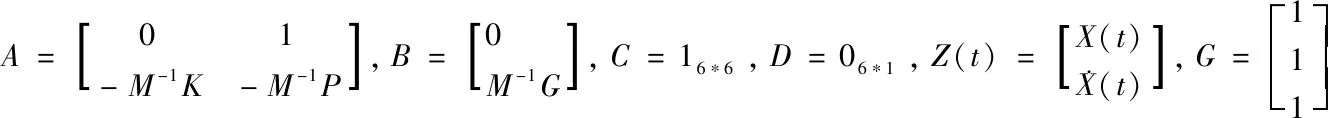
三自由度机械振动系统仿真模型如图2所示:
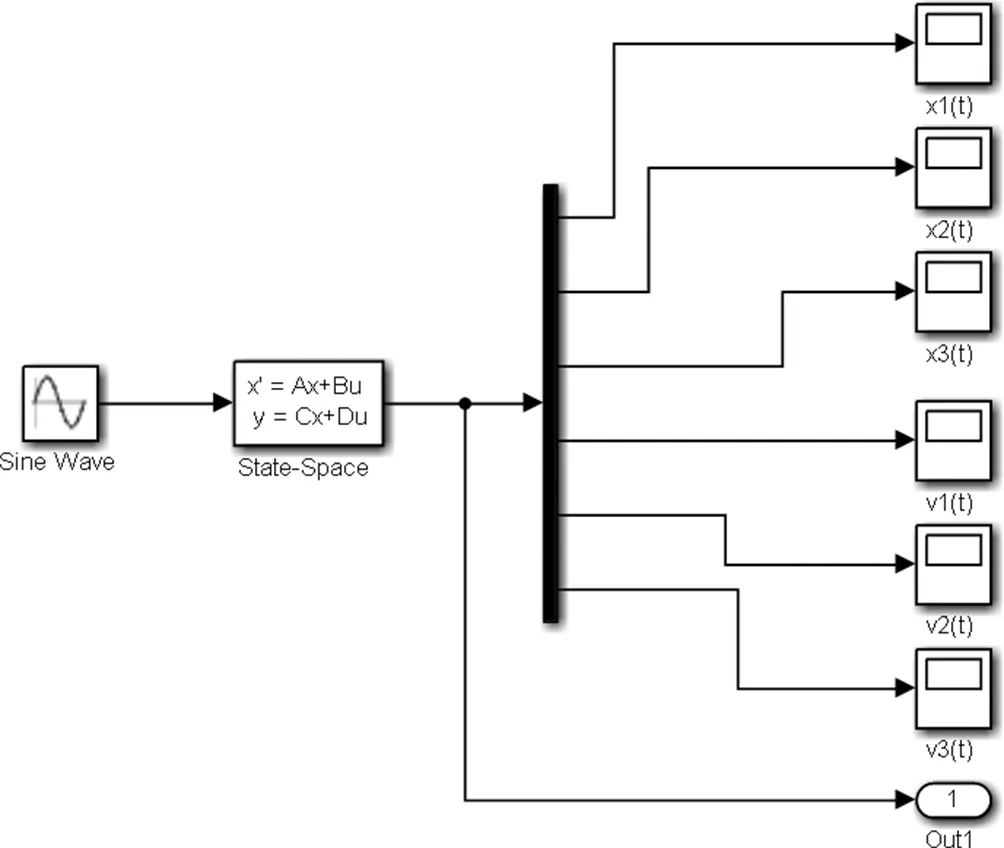
图2 三自由度机械振动系统仿真模型
提取位移和速度随时间变化关系的仿真数据[5],得到位移随时间变化曲线图3和速度随时间变化曲线图4如下:
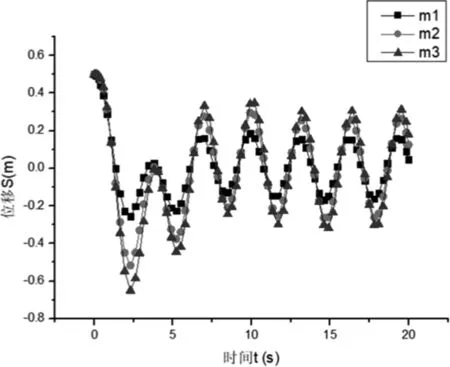
图3 位移随时间的变化关系
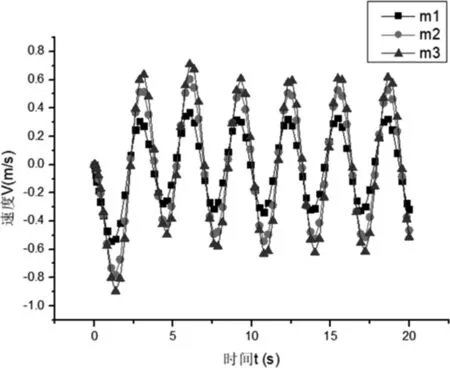
图4 速度随时间变化关系
由变化曲线可知:m2和m3开始的振幅和速度比m1大,稳定后的振幅和速度是m3最大,m1最小
本文对三自由度机械振动系统进行了数学建模及simulink仿真,对仿真数据进行提取得到位移和速度随时间变化关系曲线。

