基于动态Vague集的Web网络流量监控研究
迟江波, 刘利波
(新疆轻工职业技术学院 继续教育学院, 乌鲁木齐 830021)
0 引言
计算机和互联网技术在人们日常工作及生活中的应用不断普及,给人们生活水平的提高和社会的进步发展带来了巨大的改变,由此网络安全问题也逐渐成为人们研究的热点。目前,在网络安全问题的表现中,一个主要的表现就是网络异常变化。部分网络安全学者认为,网络入侵或导致网络流量异常,因此网络异常检测的核心,就是网络异常检测模型。目前,针对网络异常检测模型的选择中,比较常见的算法包括小波分析、SVM支持向量机、决策树等算法。如吴锐(2017)等则提出了一种基于SVM的电信网络异常检测方法,从而通过SVM的分类,完成对网络异常的监测[1];崔嘉(2017)则采用决策树判断方法,完成了对P2P网络异常的监测[2]。本文则结合当前的网络异常检测模型,提出一种基于动态Vague集的网络流量异常监控,并对该方法的可行性进行了详细的验证。
1 Vague集理论描述
自模糊集理论诞生以来,通常将其应用于对不确定性信息的处理,即在信息不完备的情况下,采用模糊集的方式来进行描述。但由于模糊集仅能描述集合中各元素对于该集合的隶属度,因此难以反映对命题的否定与模糊程度。针对这一问题,K. Atanassov于上世纪八十年代提出直觉模糊集理论,即Vague Set理论。该理论的核心思想是通过构建隶属度与非隶属度来计算得到对命题的支持及反对的度量[3-5]。在本研究中,讨论的是在流数据不完备的情况下对网络异常进行判断,即可以采用直觉模糊集的方式,完成对网络异常的描述,进而选择此异常方法。由此,对于任意x∈U,若可计算出{〈x,μA(x),νA(x)〉:x∈U},则得到一个论域U上的Vague Set,其中,μA为对论域U上的命题A的支持度量,νA为反对度量,支持度量和反对度量两者满足以下关系,如式(1)—式(3)。
μA:U→[0,1]νA:U→[0,1]
(1)
μA(x)+νA(x)≤1
(2)
πA(x)=1-μA(x)-νA(x)
(3)
式(3)中,πA(x)表示对论域U上的命题A认知的不确定性。
综上所述,Vague集就是通过0~1之间的两个数定义一个区间,描述反映所收集的信息对命题A的支持度量与反对度量,从而为决策者提供有力的信息支持。
2 基于动态Vague集的网络流量异常监控模型构建
目前,虽然部分网络异常流量监控模型取得好的检测效果,但是在流数据如果不完备的情况下,赫熙煦(2018)认为传统模型很容易造成识别率低的问题,从而会导致对异常检测的误判,最终不利于网络异常的监测[6]。同时,在异常检测中,考虑到时间因素是分析及解决问题的关键维度之一,对规则或知识的变化有着极大的影响作用。对此,在本文中则结合时间温度,进而构成一个动态Vague集,然后运用认知模型中的真假隶属函数来完成对Vague集数的构建。
2.1 动态Vague集定义
假设时间变量为t,动态Vague变量为α(t)=μα(t),να(t),πα(t)),对于在确定的时间变量t下,满足以下关系如式(4)。
μα(t)∈[0,1],να(t)∈[0,1],μα(t)+να(t)≤1,
πα(t)=1-μα(t)-να(t)
(4)
从上述定义可以看到,假设有t=t1,t2,…,tp个时间段,则得到p个Vague集数α(t1),α(t2),…,α(tp)。而通过以上的定义,得到了一个关于时间因素的Vague集。
2.2 频度因子
除了时间因素以外,事件发生频度同样是分析及解决问题的关键维度之一。比如通过统计在同一个IP地址下出现攻击的次数,那么我们可以判断其发生网络异常的概率。因此,本文则引入频度因子,以挖掘网络运行中发生异常的潜在规律或者是因果关系。而在频度因子中,平均间隔时间t0和平均次数n0是衡量频度的重要指标。频度动态因子计算为式(5)[7-10]。
FParamdynamic=
(5)
式中,t0为某类事件的平均发生间隔,n0该类事件平均发生次数。
2.3 相关因子
为提高异常监控识别判断的准确率,引入事件相关因子。在相关因子计算中,相关联度r与关联频度f是关键参数。前者描述不同事件间的关联性,与后者结合得到相关因子,以提高判别的准确性。具体计算为式(6)。
RParamdynamic=
(6)
3.4 动态Vague集认知模型构建
通过以上的定义,为当前Vague集的描述增加了一个新的角度。而从认知理论的角度认为,任意事件都是独立的,在对事件的分析中,我们采用时间因素和相关因素作为加权因子,从而对事件进行分析。因此,在对动态Vague集认知模型的构建中,由基础认知集数和动态认知权值来共同对事件进行描述,以提高识别的准确率。
基础认知Vague集数定义为式(7)、式(8)[11-13]。
{〈x,μC(x),νC(x)〉:x∈U}
(7)
动态认知的权值:
α(t)=(χ(t),λ(t))
(8)
动态认知为一个整体函数,因此在计算的过程中,需要对基础认知Vague集数进行修正。式(8)中,χ(t)和λ(t)分别描述了动态认知对于真实隶属函数和虚假隶属函数的证据支持度。
将基础认知与动态认知结合后,得到动态认知Vague集数,以此反映对最终决策信息的支持度式(9)。
Vaguedynamic={1-(1-μC(x))χ(t),νC(x)λ(t),
(1-μC(x))χ(t)-νC(x)λ(t)}
(9)
3 算法描述
由此,通过以上的构建, 我们将动态认知的Vague 集网络异常监控算法设计为如图1所示。
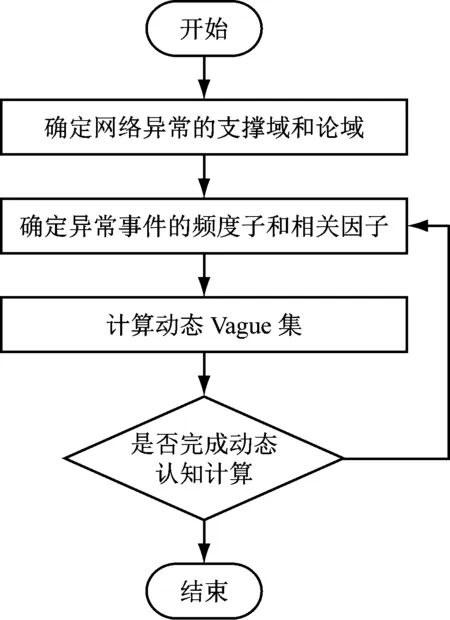
图1 基于动态认识的Vague集网络异常监控算法
4 算法验证
为了验证上述算法的有效性,本文以比较传统的Kddcup99数据集进行挖掘,然后使用IPv6实际的网络流量数据进行分析,并将其与部分厂商的监测结果进行对比,以验证上述算法的可行性。
4.1 完备Kddcup99数据集实验
Kddcup99数据集目前普遍应用于网络安全算法的验证中,而为了验证动态Vague算法,以当前主流的SVM分类算法来进行比较。评价指标则选择准确识别率和运行时间。在试验平台选择方面,使用酷睿i7,内存大小8G的windows7操作系统作为试验平台。通过对Kddcup99数据的预处理,对数据进行离散化,进而得到服从正态分布的数据集[14-16]。同时分别应用动态Vague算法和SVM算法对网络流量异常数据进行识别,从而得到表1和表2的结果。

表1 识别准确率数据

表2 运行执行时间
从以上结果看到:与SVM相比,本文提出的动态Vague算法的运行时间更长,说明本文算法在运行时间上,不具备其优势。
4.2 不完备Kddcup99数据集实验
在不完备Kddcup99数据集的情况下对算法进行验证,得到在缺失率分别为10%、25%,采样率分别为10%、30%下的实验结果,具体如表3所示。
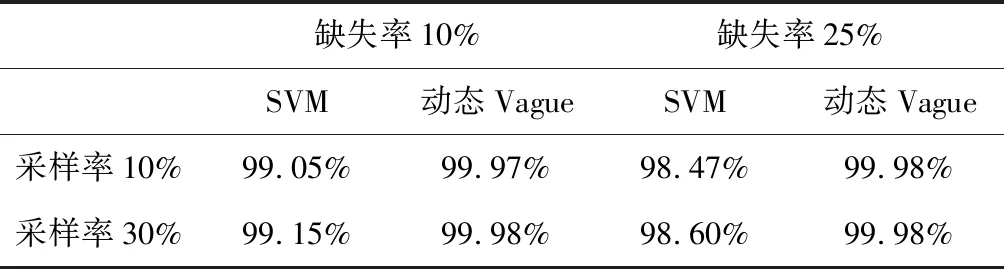
表3 不完备Kddcup99数据集实验结果
从表3所示可以看到:在同一缺失率的情况下,SVM与动态Vague算法在10%、25%采样率下的准确率只存在极小的差异;相较而言,在10%采样率下的准确率略低于在30%采样率下的准确率;SVM在25%缺失率与10%缺失率下的准确率相比,有着较大的下降幅度;动态Vague在不同缺失率的情况下,准确率未出现显著变化。由此说明,本文构建的算法在缺失率越大的情况下,其结果差异不大,说明其准确率越高。
4.3 真实环境下的流量异常检测结果
上述的分析是以Kddcup99数据集作为试验,缺乏对真实环境下的网络流量异常监控。对此,本文则以我职业院校在2018年1月~2018年4月的真实流量数据作为基础,分别运用SVM算法和本文构建的算法进行对比,如图3所示。

图3 不同算法下的识别记录数
通过上述的对比看出,本文构建的算法与网络安全设备识别的网络异常记录非常接近,说民本文算法的有效性。
5 总结
本文针对现有网络流量异常监控方法在不完备数据和流数据处理方面所存在的问题,在动态Vague集基础上,构建了频度因子与相关因子,得到动态认知Vague 集。该方法能够充分考虑到时间因素的影响,并通过相关度来提高识别准确率。实验结果说明,该算法能够准确有效地处理不完备数据和流数据。此外,该算法在运行效率方面仍有较大的优化改进空间。
——入侵植物响应人为扰动的适应性进化方向探究

