高新企业信用违约风险的探究
张瑞雪 屈尔屾

【摘要】 随着经济的发展、社会的进步、科技和信息化水平的提高以及全球资源和环境问题的日益突出,高新技术产业受到越来越多的关注。文章通过锐思和国泰安数据库,以高新技术产业的代表公司——青岛东软载波科技股份有限公司2016—2018年前三季度对外披露的数据为基础,利用KMV风险计量模型计算其违约距离和预期违约概率,从而为高新技术产业的发展提出建议。
【关键词】 信用风险;KMV模型;违约距离和预期违约概率;高新技术产业
【中图分类号】 F275 【文献标识码】 A 【文章编号】 1002-5812(2019)22-0040-03
一、信用风险简介
众多研究和实践表明,信用风险和金融市场的发展趋势有着密切的联系。信用风险,通常被定义为债务人在合约规定期限内没有按照约定日期将本应归还的本金和利息偿付给贷款方,从而给债权一方造成了不同程度的经济等方面损失的风险。为了更好地保障债权人的权益,对信用评级衡量方式和方法的研究在学术领域和实务层面逐渐兴起和发展起来。信用评级将构成要素复杂的各类市场上的信息经过一定的处理和加工,进而生成一些更方便于使用方理解的各类信息种类产品,并通过这种方式给各类金融市场输出更多有价值的信息服务。
一段时间以来,隐形和刚性两种特性的兑付预期导致债券市场上投资人在规定时间内都将企业的收益率放置在首要位置上,其直接后果是众多信息使用者在一定程度上不重视企业的信用风险,信用风险的定价机制被严重扭曲,信用评级的市场效力被弱化。隨着我国市场经济的不断发展,在对相关的金融产品进行定价分析、合理有效配置资源等方面,信用评级都具有极其重要的应用,甚至对增强市场有效性、消除信息不对称等层面上也有着至关重要的作用。
虽然经过多年的发展,我国的信用评级有了长足的进步,评级业务的规模范围在不断扩大,相关的业务种类也在不断丰富,但信用评级市场的主力份额仍掌握在海外的评级机构手中。基于此,提高我国信用评级业务水平,促进信用评级业务在我国的发展,对维护资本市场国际环境中中国的金融主权至关重要。
信用评级的方法对于信用风险衡量至关重要,是信用风险评判的核心要务。从信用风险评测的模型角度来分析,目前信用风险评级方法可以分为传统和现代两种模式的度量方法。我国的信用风险评级方法主要包括专家制度模型、Z值评分模型、ZETA模型等传统度量方式。但信用风险由于概率分布具有向左倾斜并伴有肥尾现象出现在函数线左侧,故此我们不能用正态分布的假设来应对信用风险评测的问题。另外难以量化的道德风险对信用风险的形成有重要作用和较难对信用风险定价、信用风险的明显非系统性等特征,使得现代金融市场对信用风险评测方法的实际要求日渐提高,更多优秀的现代风险评测模型应运而生,并得到广泛的使用和不断优化。
二、KMV信用风险度量概述
1994年,J.P.Morgan提出用VAR风险价值评估为度量基础,来衡量市场的信用风险。VAR(风险价值评估)其通常理解下的含义为在正常的市场环境下,金融资产和证券组合投资带给投资方最大程度的损失可能。进一步而言,在置信区间确定的情况下,风险价值评估指标VAR值在未来特定的一段时间期限内,金融资产或者价值组合价值带给投资者损失的最大可能性。
随后,1997年J.P.Morgan又进一步提出以信用风险的量化度量为基础的信用风险管理模型,在此之后,另一类型的信用风险度量模型被瑞士信贷银行推出,与此同时,以预期违约频率(EDF)为核心度量手段的KMV模型被旧金山KMV公司研发出来。
KMV模型是一种用来估计借款企业违约概率的方法,该模型认为,债务人的资产市场价值可以决定该债务人贷款的信用风险。但是在实际的市场交易中,资产的市场价值很难真实地被反映出来,换言之,债务人的资产市场价值不能直观地被观测到。为此,KMV模型选择从另外的角度来研究评测银行的贷款问题,将目光转换到借款企业所有者的角度,由此思考归还贷款的信用风险问题。KMV模型是利用现代期权定价理论建立起来的对借款企业违约可能性进行预测的模型,KMV模型的出现具有划时代意义,是对传统信用风险度量方法的一次重要革命。
KMV模型认为,在债务到期日,如果公司资产的市场价值高于公司债务值(违约点),则公司股权价值为公司资产市场价值与债务价值之间的差额;如果此时公司资产价值低于公司债务价值,则公司变卖所有资产用以偿还债务,股权价值变为零。KMV模型的独特优点在于将现代期权理论基础作为基石,充分地使用资本市场的现有信息作为指标预测,而不是用已经产生的历史财务数据进行僵化的回顾分析,KMV模型的另一大优点就是将资本市场的实时信息充分利用到信用风险评定中,通过违约距离和违约概率的预测,更全面详实地反映上市的借款企业全面的信用状况。从信用风险评测角度,KMV模型预测思想是对传统方法改革的里程碑式进步。
KMV模型作为动态模型的一种,在衡量上市公司信用风险中,以股票债券市场的实际数据为主要分析依托,因为这一原因,使用KMV模型进行信用风险预测可以使预测数据更新,预测结果也更接近实际的经济情况,信用风险评测的结论更具有前瞻性。运用KMV模型对上市企业的信用风险进行预测时需要确定该公司现时的资产结构,一旦确定随机过程中企业的资产价值,便可以据此计算在任意一个时间单位上上市企业的实际违约概率。
但是KMV风险度量模型在实际操作中也存在一些不可忽略的缺点。首先,KMV模型成立的假设前提相对苛刻,因为资产的收益曲线分布并不满足正态分布假设,资产收益分布的数据图像实际上存在“肥尾”现象,所以KMV模型在使用过程中仅着重强调了违约预测,却没有将企业信用品质的动态变化作为着重考虑的关键点。其次,KMV风险信用模型忽视了信息不对称情况下的道德风险因素,这使得指标测量出现僵化不能完全反映市场信息的可能。
此外,KMV信用风险评测模型必须使用估值技术来获得资产价值、企业资产收益率的期望值和波动性,这导致模型预测出的信用风险对非上市公司因使用资料的可获得性差,预测的准确性也较差,另外,在处理例如期权、外币业务时,使用KMV模型预测的方法适用性较差。基于此,本文着重介绍KMV模型对信用风险的预测分析,并对该模型的数理推导和实际应用进行相应的介绍。
三、KMV信用风险模型在青岛东软载波的应用
本文以高新技术产业的代表性公司——青岛东软载波科技有限公司(以下简称青岛东软载波)为例,对其在KMV模型下的风险度量问题进行探讨,分析是否可以将KMV模型作为一种行之有效的预测模型作用在高新技术产业中。
(一)KMV模型在青岛东软载波信用风险度量中的应用
本文的目的是验证KMV模型在中国高新技术产业上市公司中是否适用,可否有效验证高新技术产业上市公司的违约距离和违约概率,且预测出的违约距离和违约概率可否正确反映高新技术产业上市公司的财务状况。
由于某些历史遗留问题,我国的上市公司某些数据缺失,这就导致了大部分研究者只能退而求其次来依靠经验性的公式:违约距离=(资产的市值-违约点)/(资产市值×资产波动率)计算近似的违约率,而不能直接使用KMV模型的方法来计算违约距离和违约概率,因为在我国使用KMV模型过程中存在着一定的适用性的问题,这也是本文研究这一问题的一个首要原因。同时在研究KMV模型时发现,高科技企业违约距离自身可以作为标准化指标来使用,KMV模型决定了违约距离越小,企业的违约率越大,反之则相反。因此,可以研究KMV模型的違约距离来研究KMV模型在我国上市公司应用的可行性,验证KMV模型的有效性。
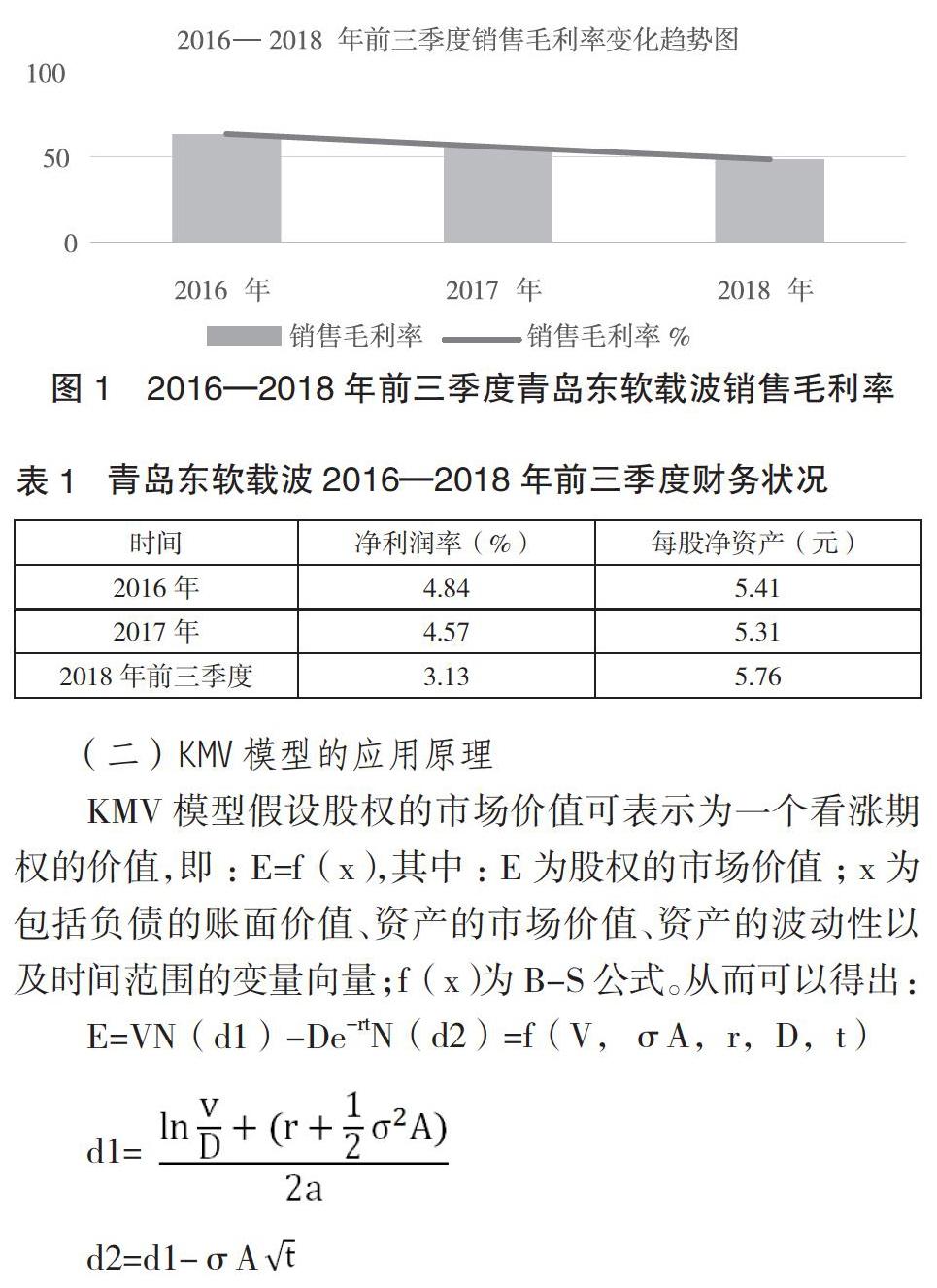
本文选取青岛东软载波进行分析是因为该公司上市时间较长,经济状况较稳定,披露信息较及时,在高新科技产业领域具有代表性。从该公司2016—2018年前三季度利润表的垂直分析来看,营业成本从2016年的占比36.34%上升为2017年的44%,同比增长7.66%;营业税金及附加从2016年的1.56%增长为2017年的1.32%;销售费用从2016年的8.57%增长为2017年的11.24%,同比增长2.6%;管理费用从2016年的21.19%增长为2017年的27.09%,同比增长5.9%;财务费用从2016年的负2.33%增长为2017年的负3.13%,同比增长0.8%;营业外收入从2016年的占比6.46%下降为2017年的0.03%,同比下降6.43%。
(二)KMV模型的应用原理
KMV模型假设股权的市场价值可表示为一个看涨期权的价值,即:E=f(x),其中:E为股权的市场价值;x为包括负债的账面价值、资产的市场价值、资产的波动性以及时间范围的变量向量;f(x)为B-S公式。从而可以得出:
其中:V表示公司资产的市场价值;σA为资产价值的波动性;DP表示负债的账面价值(即违约点DPT);t为时间范围,即到期时间;r代表无风险借入或贷出利率;N是正态分布的累计概率密度函数。
(三)KMV模型应用时参数选择
1.无风险收益率r的选择。在前述的推导公式中,r值表示选取的无风险利率,本文采用2010年到2018年中债估值中心发布的一年期国债收益率视为无风险利率的平均值作为无风险利率r的取值。2010年到2018年之间的一年期国债收益率每年的风险收益率的部分如表2所示,通过取加权平均值的计算,可以得出r=2.85%。
2.青岛东软载波的股权市场价值计算。本文在对高新技术产业上市公司的风险预测中,采用非流通股股数与基准日收盘价的乘积求得,将总股数与已上市流通股股数的差额视为非上市流通股股数,公式表示为:公司股权市场价值=流通股股数×基准日股票市场收盘价+非流通股股数×每股净资产。
如表3所示,2016年和2018年前三季度青岛东软载波的股权市场价值计算过程如下所述:
2016年青岛东软载波已经上市流通的股票股数总数为44 5448 000股,非流通股股数为7 816 857股,2017年12月30日的日收盘价格为24.72元,2017年报告期内每股净资产为4.84元。根据公司股权市场价值计算公式,计算结果为11 049 308 147.9元。
2017年青岛东软载波已经上市流通的股票股数总数为449 356 425股,非流通股股数为3 908 432股,2017年12月29日的日收盘价格为19.22元,2017年报告期内每股净资产为5.73元。根据公司股权市场价值计算公式,计算结果为8 659 025 803.9元。
2018年前三季度,青岛东软载波A股股数总和为470 309 857股,其中包括已经上市流通的股票股数总数为453 264 857股,非流通股股数为17 045 000股,2018年9月28日的日收盘价格为13.61元,2017年报告期内每股净资产为5.64元。根据公司股权市场价值计算公式,计算结果为6 265 068 503.8元。
3.青岛东软载波股票价值波动率(σ_E)的计算。在我们进行实际取数计算时,动态模型不符合客观的经济发展状况,故此本文采用的方法是使用移动平均模型对青岛东软载波波动率进行计算,换句话说,本文先使用基准日的前半年的每天的股票价格来计算波动率,然后通过对每日波动率的取得最终确定它们的平均值。本文在计算青岛东软载波股票波动率时,假设股票价格服从对数正态分布,由于一周股市开盘只有五天,所以我们近似一年股市的交易日θ=250天,计算公式如下:
设:股票收益率为ui,可得公式为:ui=lnsi/si-1。其中Si表示第i天股票的收盘价格,Si-1表示第i-1天股票的收盘价格。另根据KMV模型的推导,我们可以得出上市公司资产市场价值波动率与股权市场价值波动率的关系:
σE= N(d)σA
N(d)为0到1之间的标准的累积正态分布函数,基于上述公式,可以手工求出青岛东软载波2016—2018年前三季度市场价值波动率。详见表4。
4.债务时间参数的确定。本文设定的研究期间是1年,即计算1年期的违约距离与预期违约距离。
(1)对青岛东软载波违约距离与预期违约概率的计算。将上述公式得出的结果代入KMV模型的计算程序中,利用MATLAB软件迭代分析函数对KMV模型展开运算,最后得出青岛东软载波在2016年到2018年不同年份所对应的违约距离DD和预期违约概率EDF。通过国泰安数据库可以查询到青岛东软载波2016年到2018年前三季度的短期负债(STD)和长期负债(LTD),根据违约点计算公式可以计算出违约点的具体数额,违约点计算公式如下:
DPT=STD+0.5LTD
违约距离DD=(资产的市值-违约点)/(资产市值×资产波动率)
(2)青岛东软载波违约距离与预期违约概率计算结果与分析。
根据下页表5违约距离与预期违约概率的计算结果,可以绘制图2净利润率与青岛东软载波违约距离的变化折线趋势图。从中可以看出,青岛东软载波的盈利趋势在2018年前三季度相对于2017年有下降的趋势,净利润水平在2017年达到近三年最高水平。违约距离一直呈现下降趋势,由此可以看出青岛东软载波在近三年违约风险相对减少,2017年净利潤水平的提高直接导致了同年信用风险的降低,直至2018年前三季度,虽然净利润率下降,信用风险仍然在稳定下降,企业整体发展较平稳。
四、结论与建议
由上文的计算分析结果可以看出,KMV模型可以在一定程度上反映高新技术产业上市公司盈利状况和信用风险的关系。由此,可以通过KMV模型计算违约距离和违约概率,估算出企业的信用状况和违约风险,商业银行也可据此作为对上市公司减少信贷风险的一种有效手段,进而增强金融市场的稳定性。
但这也对我国高新技术产业公司提出了一定的要求,必须保证企业对外披露信息的可用性和可靠性。海外的高新技术企业常使用预期违约率EDF来衡量自身信贷风险,但由于国情不同,所以国外的方法在我国可否适用仍需进一步讨论。
【主要参考文献】
[1] 王亮亮,王跃堂.企业研发投入与资本结构选择——基于非债务税盾视角的分析[J].中国工业经济,2015,(11).
[2] 舒谦,陈治亚.治理结构、研发投入与公司绩效——基于中国制造型上市公司数据的研究[J].预测,2014,(03).
[3] 马文聪,侯羽,朱桂龙.研发投入和人员激励对创新绩效的影响机制——基于新兴产业和传统产业的比较研究[J].科学学与科学技术管理,2013,(03).
[4] 李静,彭飞,毛德凤.研发投入对企业全要素生产率的溢出效应——基于中国工业企业微观数据的实证分析[J].经济评论,2013,(3).
[5] 朱洁,李齐云.信用风险视角下地方政府债券发行规模测算——基于KMV模型的实证分析[J].中南财经政法大学学报,2016,(02).
[6] 邓殷洁,胡丹云.基于KMV模型的地方政府债券信用风险度量——以北京市地方政府债券为例[J].现代经济信息,2015,(24).

