对一道模考把关试题的分析

安徽省铜陵市第一中学 (邮编：244031)

1 题目呈现

2019年合肥市包河区中考一模第23题为：

图1

图2

图3

已知△ABC中，BC=a,AC=b,AB=c,∠ACB=2∠B,CD是∠ACB的角平分线.(1)如图1，若∠A=∠B，则a、b、c之间的关系是；

(2)如图2，求证：c2-b2=ab；

2 解法探究

2.1 第(1)小题

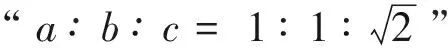
2.2 第(2)小题

第(2)小题的实质就是证明“△ABC中，若∠C=2∠B,则c2-b2=ab”.这是三角形中由角度关系向边长关系转化的经典问题，我们可以从三角运算和几何方法两个方面考虑.由于三角运算，涉及边角关系和正、余弦定理，属于高中知识，这里不再展开.

以下从几何关系方面展开探究.

方法一(母子相似)

评析本证法根据题目所给的角平分线寻找相似三角形，再利用比例性质进行变形到达证明目标，与参考答案方法一致.

图4

方法二(另一组母子相似)

如图4，延长AC至E,使得CE=CB.

由于∠E=∠CBE,

所以∠ACB=2∠E=2∠ABC=∠ABE.

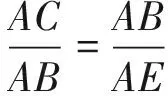
整理得c2-b2=ab.

评析本证法是利用形外作辅助线寻找相似三角形，构图上另辟蹊径，方法巧妙自然.

图5

方法三(托勒密定理)

如图5，构造等腰梯形ACBE,则C、D、E三点共线.

由∠ACB=2∠CBA=∠CBE得∠CBA=∠ABE=∠BAE,所以AC=BE=AE=b.

由于等腰梯形ACBE是圆内接四边形，

所以根据托勒密定理得AB·CE=CB·AE+AC·BE,

即c2=ab+b2,移项得c2-b2=ab.

评析本方法先构造一个等腰梯形ACBE,再利用托勒密定理完成证明，高效直接.

方法四(张角定理)

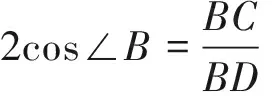
整理得c2=ab+b2,即c2-b2=ab.

评析本方法先利用张角定理的角平分线的特殊状态，再引入边长关系运算，体现了几何法与代数法完美结合.

2.3 第(3)小题

评析①这里CD+BC=AC需要证明，方法可对AC截长，也可以对BC补短，其细节留给读者；②本方法通过三角形的相似比引入边长运算，再结合边的长度之间的特殊关系CD+BC=AC代入完成证明.

方法二如图6，在BC的延长线上，取一点E,使得∠EAC=∠CAB,

容易证明∠E=∠ACE=3∠A,所以AC=AE=b.

在△ABE中，AC是角平分线，

图6

评析本方法通过形外作图由三角形内角平分线定理引入边长运算，再结合角的特殊性得出边之间的相等关系代入完成证明.

方法三由∠ACB=2∠B得c2-b2=ab,即c2=b(a+b)；

又∠B=2∠C,同理可得b2-a2=ac,即ac=(a+b)(b-a).

评析本方法要求对已知条件作充分挖掘，深刻理解并灵活应用第2题的结论.进而得出两个代数式，再对它们联立进行适当变形完成证明.体现出逻辑推理、运算求解、创新思维等多重数学能力.

3 本质探索

3.1 图形生成过程

本题的本质核心是△ABC中，∠ACB=2∠B这一几何关系与c2-b2=ab的代数形式等价.要想处理好这里面的推理关系，充分探索满足∠ACB=2∠B的△ABC的几何构型成为关键.从角的关系来看，可以从平分∠ACB或者加倍∠B从而产生等角这两个思路下手.

方法一(作角平分线)

作∠ACB的平分线交AB于D,

由∠ACB=2∠B得∠ACD=∠DCB=∠B,于是∠ACD=∠DCB且DC=DB.

所以我们可以这样理解原题图形的形成过程：

图7

如图7，先在以D为圆心，DB为半径的圆上取一个动点C形成等腰△DCB.再以CD为对称轴，作出CB的对称直线CA交BD的延长线于A.

注意①由上即可得出原题的第1和第3小题是动点C在圆上的不同特殊位置形成，其中第1题最为特殊，此时∠CDB为直角，△ACB为等腰直角三角形；②按照这个思路不变，图形也可以换个生成的方式，在∠ACB的角平分线上取一点D,再以D为圆心，DC为半径作圆交BC于B,BD的延长线交CA于A；③CA也可以看做是等腰△DCB外接圆在点C处的切线.

方法二(以AB为轴作轴对称)

作BC的垂直平分线，设点A关于垂直平分线的对称点为点D,AD、BC的中点分别记为M、N.易得:ADBC为等腰梯形且AC=AD=DB.

图8

所以我们也可以这样理解图形的形成过程：

如图8，先作一个等腰梯形ADBC且AC=AD=DB(作法略)，而△ACB就是等腰梯形ADBC除去两条相等的邻边AD、DB形成△ADB所留下来的图形.

评述第2题解法六中构造等腰梯形的做法就是基于这样的图形理解.

方法三(以BC为轴作轴对称)以BC为对称轴，作出BA的对称直线BE交AC于E.

由于∠ACB=2∠ABC=2∠CBE,所以∠EBC=∠CBE.

所以我们还可以这样理解图形的形成过程：

图9

如图9，先作∠XBy的角平分线，以角平分线上一点C为圆心，CB为半径画圆交By于E,EC与Bx的交点设为A.

评述①第2题解法二形外作辅助线就是基于这样的图形理解；②注意方法三与方法一形成的关系，他们的本质是相通的.

3.2 等价条件分析

通过以上的探究可以得出：在△ABC中，以下条件任意两个等价①∠C=2∠B,②c=2bcosB,③b=a-2bcosC,④c2-b2=ab.

值得注意的是，上述4个条件都是关注三角形的基本元素.其中条件①是纯粹角的倍数关系，条件④是纯粹边的关系，条件②、③是边和角的混合关系，它们虽然形态各异，但是都简洁直观，体现出联系的本质.除此以外，笔者还以∠C=2∠B这一条件得出一些几何关系，前提是引进一些新的点或线段，具体的有(图略)：

(1)若AE是∠A的内角平分线，E在BC上，则AB=CE+AC；

(2)若AF是∠A的外角平分线，F在BC延长线上，则AB=CF-AC；

(3)若AH是BC边上的高线，点M为BC边的中点，

则①AC=2HM,②当∠C≤90°时，BH=AC+CH,

③当90°<∠C≤120°时，BH=AC-CH；

(4)过A作∠C的内角平分线的垂线，垂足为G,则AB=2CG.

4 特色分析

每一道优秀的把关试题的产生，一定是经历了命题组专家辛苦的思考，凝聚了集体的心血与智慧.下面我们来分析这道把关题的特色.

本题立足基础，强调解决问题的通性通法.《义务教育阶段数学课程标准(2011版)》指出，学生掌握数学知识，不能依赖死记硬背，而应以理解为基础，并在知识的应用中不断巩固和深化.试卷既然选择让平面几何题作为把关题，就应该立足于初中的基本图形，着眼于解几何题的基本方法，注重考查逻辑推理、数学转化与化归等基本能力. 本题涉及的知识点、几何图形与解决办法都是基本的，突出了对通性通法的重点考查，同时在思维的考查上又分量十足，充分体现出把关题的功能.

本题综合适当，准确考查学生数学核心素养.作为初三毕业班模考的把关题，必须要具有适当的综合性，综合性稍强的试题不仅可以考查学生对多个知识点的掌握情况，更可以考查学生分析问题解决问题的关键能力. 当然把关题的综合性要自然、得体，过轻达不到考查效果，过重则增加考生负担，都会影响试题的效度.本题综合了相似三角形的判定和性质、代数式的变形等多个重要知识点，对学生方法、能力的考查也恰如其份、适中得体，能准确地达成考查的目标.

本题属于老题新编，精心设计富有探索性的问题. 由于中学数学知识内容的局限，考试中不可能也没必要全面回避经典问题，然而我们关注是的如何用专业的命题技术，使得这些老问题为今所用，起到预期的考查效果.笔者查阅相关资料，发现上个世纪八十年代的数学竞赛中就有很多类似的试题，收集如下：

①(1980年上海市中学生数学联赛)在△ABC中，最大角A是最小角C的二倍，夹角两边b=5,c=4,求第三边a和三角形面积.

②(1985年新加坡中学数学竞赛)设ABC是一个三角形，∠A=4∠C,∠B=2∠C,求证：(BC+AC)·AB=BC·AC.

③(1985年中国高中数学联赛)在△ABC中，角A、B、C的对边分别为a、b、c,若角A、B、C的大小成等比数列，且b2-a2=ac,则角B的弧度数等于.

④(第10届IMO)证明：边长为三个连续自然数，且一个内角是另一个内角两倍的三角形有且只有一个.

本题的设计中，第一问是一种特殊状态，同时也为证法二的讨论提供素材支持，引发学生对特殊性的关注.第二问中角平分线能进一步启发学生思维，引导学生从几何的角度分析试题，实属点睛之笔.第三问的本质是倍角的嵌套，如果学生有很好的发现思维与分析问题的能力，就不必另起炉灶，立即从代数的方向利用2的结论就能乘势而上，势如破竹般解决问题.

由此可见，整个试题设计巧妙，特色鲜明，特殊与一般、几何与代数相互交融. 而且富有层次性、探究性、综合性. 引导学生探寻自然的思考方法，追求对数学本质与核心素养、关键能力的考查，对一线的课堂教学也起到了很好的导向作用.