如何在操作课中落实关键能力

浙江省衢州市白云学校 (邮编：324000)

2019年5月底区教研室举行了优质课评比，赛前4天公布了赛课素材：八年级下册书本第128页设计题，如下图所示.

图5-21

先准备一张矩形纸片和一张平行四边形纸片，然后尝试以下操作.

1. 把平行四边形纸片补成一个矩形. 怎样操作能使分割纸的条数最少？

2. 把矩形纸片割补成一个角为60°的平行四边形，怎样操作能使分害线最少？

通过上述活动，你获得哪些经验？

(请与你的同伴交流)

试一试：由两个正方形组成的纸处如图5-21. 把它割补成一个更大的正方形，并使分割线的条数最少.

赛课要求：请围绕课本素材，开发设计一节相关内容的小专题复习课，注意突出素材的核心思想与方法.笔者作为参赛选手参加了比赛，并取得了第一名，现把整节课的备课心路历程与大家做一交流.

1 素材分析

本素材出自浙教版课本第五章特殊平行四边形第3节正方形这一小节课后的一个设计题，学生刚好学完平行四边形、特殊平行四边形的所有知识.从素材中可看出这是一节操作课，所运用的结论是剪拼前后面积相等.如何把一节操作课开发设计成一节小专题复习课？且复习哪些知识点？是属基础复习、还是拓展提升？同时又如何突出素材的核心思想与方法？并且素材要突出哪方面的核心思想与方法呢？

2 学情分析

本次比赛是借班上课，学生来自优质生源大量流失的农村初中，已学完平行四边形与特殊平行四边形的知识，且相关复习课刚结束，全班32个学生，基础性的单元测验成绩及格以上人数达16人，即将学习下一章反比例函数的知识.

3 二次设计

3.1 第一次设计——剪拼中的学问

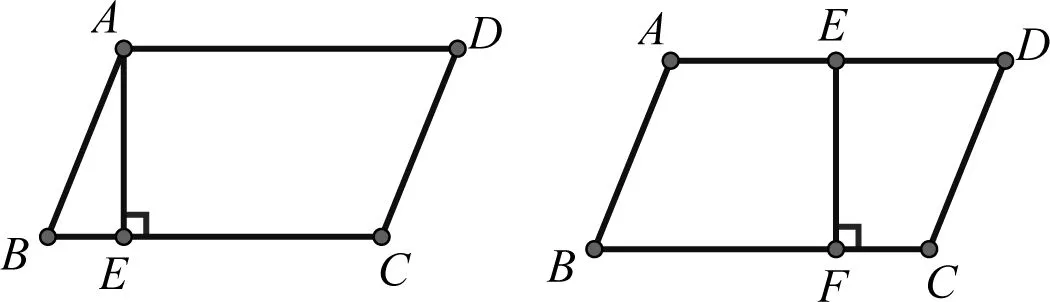
问题1 把平行四边形纸片割补成一个矩形，怎样操作能使分割线的条数最少？

图1(Ⅰ) 图1(Ⅱ) 图1(Ⅲ)

如图1(Ⅰ-Ⅱ)学生先找分割线、再动手剪拼，最后根据图1(Ⅲ)写出已知，求证，再完成证明过程.

结论：(1)形与数有联系的(面积)，数的问题(面积)可以用形来体现；

(2)剪拼问题是需要尝试调整的，最后需要对照要求检验是否符合要求.

板书：尝试——发现——表达——证明——归纳.

剪拼前后：面积相等.

问题2 反之，如果把矩形纸片割补成一个平行四边形，怎样操作能使分割线最少？

图2(Ⅰ) 图2(Ⅱ) 图2(Ⅲ)

如图2(Ⅰ-Ⅱ)学生先找分割线、再动手剪拼，最后根据图2(Ⅲ)写出已知，求证，再完成证明过程.

引导学生：按问题1收获的结论：发现——尝试——表达——证明——归纳去解决问题.

问题3 如果把矩形纸片割补成有一个角为60°的平行四边形，怎样操作能使分割线最少？

图3(Ⅰ) 图3(Ⅱ)

图4

问题4 如果用一块两边满足1∶2的矩形纸片割补成一个更大的正方形，并且使分割线最少？

问题5如果是一大一小的二个正方形，你还能拼成一个更大的正方形吗？并且要分割线最少.

图5(Ⅰ) 图5(Ⅱ) 图5(Ⅲ) 图5(Ⅳ)

如图5(Ⅰ-Ⅲ)学生先找分割线、再动手剪拼，最后根据图5(Ⅳ)写出已知、求证，再完成证明过程.

引导学生：按问题1收获的结论：发现——尝试——表达——证明——归纳去解决问题

小结

在今天的剪拼问题中，你获得了哪些经验？

(1)剪接问题是需要尝试调整的，最后需要对照要求检验是否符合要求的，即解决问题之后是需要推理论证的；

(2)数学学习方式不是唯一的，只要努力探索，你一定行；

(3)数形是有关联的，数的问题可以用形来体现，形的问题可以通过数来思考.

今天以剪拼问题为载体，我们回顾了哪些知识呢？

平行四边形，特殊平行边形的性质与判定，勾股定理，三角形全等的判定及性质.

3.2 第一次设计的思考

对照比赛要求：首先课堂上剪拼后花了很多时间证明，似乎体现了复习的味道，但只是让学生在剪拼后完成了几道证明题而已，学生只见树木不见森林，没有自身体会到复习的目的何在，没有体会到知识的价值，学习是被动的；其二直接由问题4的矩形剪拼过度到问题5，学生还没有寻找分割线的经验，跨度太大；其三比赛所要体现的核心思想在哪？学生唯一的收获是解决问题的套路：发现——尝试——表达——证明——归纳.对于发现，发现什么？怎么尝试寻找分割线，分割线的寻找有没有依据可寻？

深挖素材：为什么教材要在整一章特殊平行四边形的内容结束后安排了这个设计题？它为最后一个操作活动起到了什么作用呢？带着以上思考，有了第二次设计：

3.3 第二次设计——怎样剪拼成正方形

教学目标 :

(1)从一个简单的问题入手，引导学生发现分割线的寻找思路.

(2)从特殊到一般，学生自主发现——推理——归纳出分割线的寻找思路，从中培养学生的推理能力.

(3)通过层层深入的问题串，培养学生发现问题的能力，解决问题时的迁移能力.

教学重点：寻找分割线的形成思路.

教学难点：寻找用任意边长的2块正方形剪拼成更大的正方形分割线的形成思路.

问题1 用最少的分割线把一个平行四边形纸片割补成矩形，你会怎样操作？

预设学生能做出如下分割：

讨论：你是怎么想到这条分割线的？

形成想法：从目标图形的特征出发寻找思路.目标图形是矩形，而矩形的特征是有直角.

问题2 用最少的分割线把一个矩形割补成含有60°角的平行四边形纸片，你会怎样操作？

预设学生能做出如下分割：

讨论：你是怎么想到这条分割线的？

形成想法：从目标图形的特征出发寻找思路.

目标图形是平行四边形，特征是有600角的平行四边形.

问题3 用最少的分割线把两个边长为1的正方形纸片割补成一个大正方形，你会怎样操作？

预设学生能作出如下分割：

讨论：你是怎么想到这条分割线的？

形成想法：从目标图形的特征出发寻找思路.

归纳想法：

讨论：上述三个简单问题的剪拼方法，是如何想到的？你发现了什么？

形成方法：从目标图形特征出发寻找思路.

(说明：以上用时12-15分钟)

问题4 用最少的分割线把一个长为2宽为1的长方形纸片割补成一个正方形，你会怎样操作？

预设学生能依照问题3作出如下分割：

如果学生有困难，教师作如下引导：

(1)目标图形是什么图形？

(2)这个正方形有什么特征？

(3)正方形的面积为2，边长为多少？

问题5用最少的分割线把边长分别为1与2的正方形纸片割补成一个更大的正方形，你会怎样操作？

先让学生自主尝试，如果有的学生会，要重视让学生讲明白如何想到的.

如果学生有困难，教师作如下引导：

(1)目标图形是什么图形？

(2)这个正方形有什么特征？

(3)正方形的面积为5，边长为多少？

问题6 如下图，用最少的分割线把边长分别为a、b的正方形纸片割补成一个更大的正方形，你会怎样操作？

先让学生自主尝试，如果有的学生会，要重视让学生讲明白如何想到的.

如果学生有困难，教师作如下引导：

(1)这个问题与问题5有什么区别与联系？

(2)目标图形是什么图形？

(3)这个正方形有什么特征？

(4)正方形的面积为a2+b2，边长为多少？

归纳想法：

讨论：上述三个问题的剪拼方法，是如何想到的？你发现了什么？

形成方法：从目标图形特征出发寻找思路，关键是找到与目标正方形的边长等长的割线.

小结

你认为剪拼问题如何寻找分割线的？以剪拼问题为载体，今天我们主要复习了哪些知识？通过今天的学习，对你今后解决新的问题，有怎样的帮助？

第二次的教学设计以“找——剪——拼”这个操作流程对每个问题展开，解决每个问题时又紧紧围绕你是如何寻找分割线展开分析，首先从角度特征寻找分割线，然后从边长与角度二方面的特征寻找分割线；最后通过把相等的角重合、相等的边重合来拼接，由易到难，由特殊到一般，让学生将实际问题抽象化，抓住问题的前后联系点，先体会运用迁移、推理的能力解决一般性的问题，最后逐渐内化为一种自身的能力，并主动运用这种能力解决复杂问题.

4 教后反思

(1)关于素材的处理

数学教学，就教材教教材不行，就知识教知识也不行，必须要跳出教材、教知识，跳出知识得经验，跳出经验长智慧，所以我们的教学不仅是知识层面和方法层面的教育，而更应上升到智慧层面，素养层面的教育.而每一个素养的落实不是靠说教，要靠具体的问题，学生从具体简单的问题获得经验，然后通过递进式的问题，巩固这种经验，变成学生解决问题的一种智慧，用这种智慧去应对复杂的问题.

比如——问题1：由矩形最大特征是直角，自然想到只要在原图形中作垂直的分割线，从简单的问题入手，引导学生从目标图形的特征寻找分割线，即从角这个角度寻找分割线，且无数种分割法的共同特征都是垂直，问题2再次引导学生从角这个角度寻找分割线，只要在原图形中作60°角这条分割线即可.

而问题3，虽然是1条分割线向2条分割的过渡，但因是学生身边熟悉不过的素材，学生轻松找到2条分割线，如果说此时对要考虑2条分割线的位置与边长的关系问题核心不够凸显的话，那么问题4再次以另一个面目呈现问题3——用一个宽为1，长为2的矩形剪拼成一个正方形，通过追问，你认为这个问题与问题3有什么共同点，此时犹如涓涓细流汇成大江大海，学生因2个问题相同的本质而兴奋，发现问题4就是问题3——宽为1，长为2的矩形可以看成2个边长都为1的正方形，为后续学生解决一般性的问题做足了迁移能力的铺垫.就这样学生的迁移能力在润物细无声中得到渗透，此时再适时地追问寻找分割线时要考虑几方面的特征？——边长与角度，但当2个方面都要满足时，可以采用控制变量法，比如先满足边长，再满足角度，学生在问题1与2寻找分割线时只满足角度的特征基础上又收获了当多个变量都要满足时，先满足一个变量的寻找方法.分割线的寻找思路明朗化、清晰化、条理化.

从问题5到问题6，是学生主动运用迁移能力解决问题，一波三折，难点不攻自破，学生很快自己找到问题的方法与思路，体会到遇到复杂的一般性的问题可以从特殊到一般，从特殊的问题寻找解决问题的方式方法从而把它迁移到一般性的问题中.

(2)关于教学过程的设计

教学过程是课堂教学设计的核心，教学任务、教学目标、教学对象的分析、教学媒体的选择，课堂教学组织形式，都将在教学过程中得到体现.课堂教学要求我们关注学生的主动参与，让学生在寻找中、剪拼中、在情感的体验中，进行有效生长.在这样的理念下，整节课不是沿着“教”这条单线前行，而在“学”与“教”的交错中，按照教学目标、教学任务动态前行.为此本节课的设计有如下特点：

①情境导入——遵循从最近发展区出发

课始利用学生熟知的素材，把这作为“突破口”，找到解决新问题与学生原有知识经验的“切合点”，把解决新问题所需要的知识“同化”或“顺应”结合到已有的知识结构中，从而体会所学知识的价值.如前面3个问题，都从学生最近发展区出发，为学生提供非常自然、流畅的思维场景(通过老师提问：你是怎么寻找分割线的？)为迁移能力的发展作深入思考.

②自主式探究——凸显问题的本质

整个操作活动始终围绕“你是如何来寻找分割线的？”这一中心问题展开的迁移活动，在探究中，根据目标图形的特征寻找分割线是核心，它是有效的思维生长的载体.

由特殊到一般，有力地落实《课标》提出的“螺旋上升”不断获取推理能力的要求.

③小结反思——基于提升学生思维能力

好的课堂教学，不仅应当引人入胜，还应有发人深省，余味无穷的小结反思.课堂小结不仅仅是对教学内容进行梳理，归纳总结，理清知识脉络，还要促进知识的拓展，延伸、迁移、生长，以便实现提升学生思维的目的.

操作课，表面培养学生动手操作能力，但是更主要的是通过操作课，引领学生体会操作背后的数学思考，为什么要这么操作，操作的依据是什么，如寻找分割线的依据是什么，其他位置的分割线是否可行？它们有无共同点？有没有更简单的操作？这些都是操作课中要慢慢渗入的“最优化思想”——用最少的分割线，以及数形结能力，从目标图形的特征出发寻找分割线.

陌生的操作该怎么办？通过容易、熟悉的问题体会、启发，到小变式问题的尝试，最后运用特殊到一般、实际问题抽象化、建模、迁移能力、推理能力这些解决问题常用的手段加以内化主动解决复杂的问题，并总结出解决问题的一般性的经验，并能透过问题看本质，高站位，看到操作背后隐藏的数学知识与数学思维.这些就是操作课中要落实的关键能力.