常态化实施数学实验教学的路径和方法

丁银杰 殷容仪

波利亚曾说：“完整的数学应该包含两个侧面，一个是欧几里得式的严谨科学，另一个是实验性的归纳科学。”《义务教育数学课程标准（2011 年版）》（以下简称“2011 年版课标”）也强调“动手实践”是学习数学的重要方式，要求“学生应当有足够的时间和空间经历观察、实验、猜想、计算、推理、验证等活动过程”。因此，进行常态化数学实验教学，应该是一种有益于数学学习的应然选择。

2015 年江苏省中小学教材审定委员会审查通过苏科版《义务教育教科书·数学实验手册》（以下简称《手册》），数学实验正式进入课堂。经过近几年的实验教学实践与研究，广大教师对数学实验有了较为全面的认识，数学实验是一种有效的教学方式逐渐成为一种共识，产生了良好的效能，常态化实施数学实验教学已成应然选择。本文笔者想就常态化实施数学实验教学的有效路径和方法，谈一些想法。

一、使用数学教材中的实验素材，让数学实验走进常态化课堂

苏科版义务教育数学教科书（以下简称《数学》）注重引导学生“做”数学，设有“数学实验室”“数学活动”“课题学习”等栏目，为学生提供了充分“做”数学的机会。常态化实施数学实验教学的有效路径和方法就是要重视使用《数学》中的实验素材，让数学实验走进常态化课堂。

例如，《数学》七下“7.2 平行线的性质”，在“数学实验室”栏目设计了“画”“剪”“叠”“拼”等操作活动（如图1），这种教学设计强调动手实践，实验意图、目的都很明确，旨在帮助学生探究平行线的性质。

（图1）

我们完全可以让这个实验走进课堂，具体操作流程如下：为学生准备一些纸张、直尺、剪刀等实验材料和实验工具，采用小组合作学习的方式进行教学，学生在教师的指导下进行“画”“剪”“叠”“拼”等操作活动，既动手又动脑，真正实现手脑协同，启思明理。另外，我们也可以利用GeoGebra 等软件进行演示实验，GeoGebra 软件中的“刚体多边形”工具的“复制”功能和图形的“平移”“旋转”等变换，方便、快捷地实现演示操作。在几何直观的指引下，学生很容易完成平行线性质的探索。

二、整合实验手册与数学教材，将实验教学常态化融进日常教学

《手册》全套有5 个分册，共设计了82 个数学实验，《数学》和《手册》上的实验资源都是为了帮助学生在操作、观察、交流、思考的基础上，更好地理解和掌握教学内容。常态化实施数学实验教学的有效路径和方法就是要重视整合《数学》和《手册》中的实验资源，将实验教学融进日常教学。

《手册》中的每一个实验，目的任务明确，内容步骤完整，工具素材齐全，指南说明清晰，可直接用于教学实践，但这并不意味着需要额外安排学时专门用于实验教学。我们建议将《手册》中的实验按“融入式”和“专题式”两种方式融进日常教学。“融入式”实验教学聚焦的是课堂的某一个环节，或作为问题情境引入新知，或操作观察提出猜想，或设计方案验证结论等，可设计成相应学时的某一片段。“专题式”实验教学一般主题明确，过程完整，建议设计成一个完整的学时进行教学。

例如，以《手册》七上内容为例，给出如下教学建议（表1）：

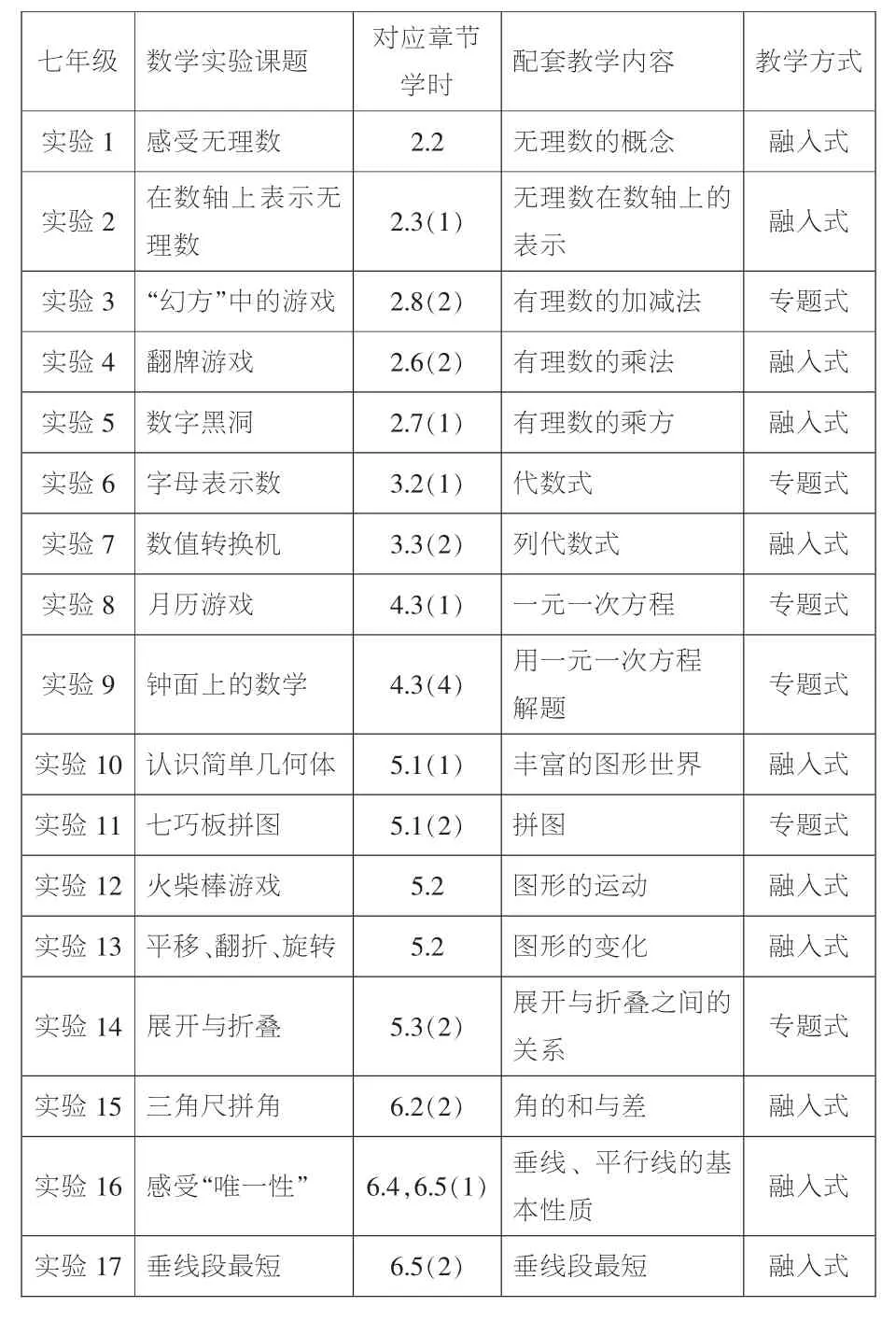
（表1）

三、信息技术与课堂教学深度融合，为常态化实验教学插上技术翅膀

2011 年版课标指出，“要充分考虑信息技术对数学内容和方式的影响，开发并向学生提供丰富的学习资源，把信息技术作为学生学习数学和解决问题的有力工具，有效地改进教与学的方式，使学生乐意并有可能投入到现实的、探究性的数学活动中去”。当前，学校信息化装备的水平普遍有了很大提升，教室一般都配有基于网络的交互式智能教学一体机，可以实现智能终端（Pad、手机等）间的信息互联互通，有的学校还建立了数学实验室，配有供学生探究的图形计算器等设备。GeoGebra、几何画板、网络画板等数学软件更是极大地提升了技术的力量。广大师生要做的是提升信息素养，了解常用硬件、软件的基本功能，掌握其使用方法，提升运用信息技术进行教学的能力。

1.信息技术与课堂教学的深度融合，让常态化实验教学化难为易成为可能。

我们建议信息技术与实验教学要进行深度融合，融合的过程中要选准融合点，避免泛化，要以信息技术之“长”，解决教学实施之“难”，化难为易，真正实现技术与教学的有效对接。

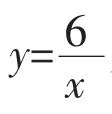
2.信息技术与课堂教学深度融合，让常态化实验教学过程中的“真探究”成为现实。

信息技术与实验教学深度融合，融合的过程就是要利用信息技术在实验教学过程中实现“真探究”，避免走过场的“假探索、真灌输”，要将学生在数学学习过程中获得的经验“迁移”到实际的问题情境，要让学生经历探究、发现、验证与应用的完整过程，以此培养学生的应用意识和科学精神。

例如，《手册》九年级分册中的“探究无盖长方体纸盒的最大容积”实验，实验目的是通过操作、比较、计算等活动，探究无盖长方体纸盒的最大容积，经历建立模型解决问题的过程，渗透逼近思想，增强数学应用意识。我们可以将实验与技术融合，发挥技术工具计算速度快、模拟精度高的优势，有效实现实验设计的意图。实验的任务与主要思路如下。

任务：将一张边长为10cm 的正方形纸片按图2 所示的方式制作成一个无盖长方体纸盒。

（图2）

探索：当剪去的小正方形边长与大正方形纸片边长满足怎样的数量关系时，无盖长方体纸盒的容积最大？

凭借已有的经验和知识储备，学生不难完成以下基础工作：（1）根据示意图，通过计算、比较，初步感知小正方形边长与容积之间的关系，（2）建立函数模型y＝x（10－2x）2，其中x（cm）为剪去的小正方形边长，y（cm3）为无盖长方体容积。但三次函数最值问题不在初中学生学习与解决的范畴中，这就需要调整认知策略，展开“真探究”。

思路1（逼近法）：经过基础工作，我们可以发现随着x 由小到大，y 先由小到大，再由大到小，y 存在最大值，这为逼近法提供了可能。在GeoGebra 的表格区先设x 的初始值为0.5，步长为0.5，计算可得当1＜x＜2 时，容积最大；再依次设定步长为0.1、0.01，得到当1.66＜x＜1.68 时，容积最大……不难发现：当小正方形边长为大正方形边长的时，无盖长方体容积最大。

思路2（图像法）：如图3，在GeoGebra 的绘图区绘出函数y＝x（10－2x）2（0＜x＜5）的图像，将x 轴与y 轴的显示比例调整为1∶50，显示图像全貌，再标出图像的极值点，显示其坐标，通过观察不难发现结论。

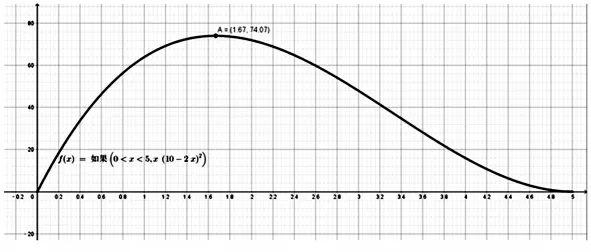
（图3）

四、课内教学与课外拓展有机结合，为常态化实验教学拓展空间

常态化实施数学实验教学的有效路径和方法还应该重视课内教学与课外拓展的有机结合，为实验教学拓展空间。可以利用学校的综合实践课程，采用课内课外、线上线下等方式，积极引导学校教师和学生深度挖掘《数学》实验资源，自主开发教具、学具，制作数学模型，不断加深对知识的理解，积累基本活动经验。

例如，初中阶段“锐角三角函数”内容，由于缺少函数图像的直观呈现，学生难以把握锐角三角函数的有关性质。针对这一情形，可以在《数学》素材的基础上，开发、制作锐角的正弦、余弦函数刻度尺教学具，在教学具的开发和使用中理解正弦、余弦的意义，感受随着锐角的增大，锐角的正弦、余弦函数值的变化规律。具体过程如下。

首先，制作刻度尺。（1）用绘图软件绘制出如图4 的图形（由宽度为1cm，量程为10cm 的角尺与半径为10cm，圆心角为90°的扇形组成），将两条半径100 等分，圆弧90 等分，标注相应的刻度与正弦、余弦标识。（2）用激光打印机将图4 打印在透明的菲林胶片上，这样就制成了锐角的正弦、余弦函数刻度尺。

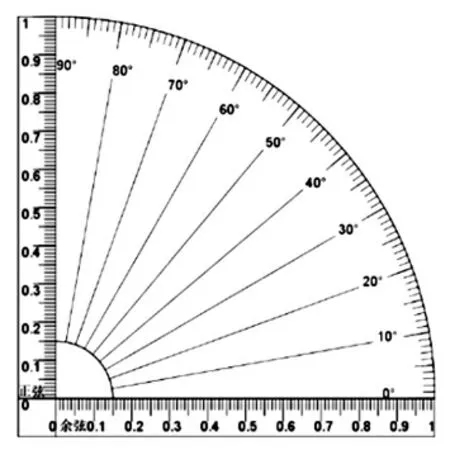
（图4）

其次，用刻度尺探究锐角的正弦、余弦函数性质。（1）说明锐角的正弦、余弦函数刻度尺的工作原理；（2）任意画出两个锐角，并用制作的正弦、余弦函数刻度尺分别量出它们的正弦、余弦值；（3）若α、β 均为锐角，且sinα＝0.60，cosβ＝0.26，能用正弦、余弦函数刻度尺估算出锐角α、β 的度数吗（精确到1°）？（4）结合（2）（3）获得的数据，有什么发现？

此外，我们还可以将数学实验的研究拓展到课外。可以将班级分成若干个学习小组，结合教学进度，有计划地引导学生进行课外数学实验探究，这些实验可以围绕课前激趣或课后梳理展开。

数学实验教学唯有“常态化”，成为师生自觉的数学教学方式，才能充分体现数学实验的价值，才能有效发展学生学科核心素养，让学生真正享受愉快而完整的数学学习过程。