微型筒式共轴双旋翼飞行器共形桨叶设计与气动仿真

危怡然，邓宏彬，江 明，潘 海，王保国

（1.北京理工大学机电学院，北京100081；2.淮海工业集团有限公司，长治046000）

1 引 言

随着电子元器件的发展、嵌入式电子领域的技术进步、能源电池性能的极大提高，无人微型飞行器（Unmanned micro air vehicle，UMAV）的研究和开发越来越容易推展，并且受到越来越多的关注。UMAV的主要目标是将人类的视野从地面扩充到天空，去执行一些高空、远距离的任务。在欧美等发达国家，已经将旋翼无人飞行器用于军事侦察、监视、通信、反潜、电子干扰等任务，在地震救灾、考古、农业、航拍等民用领域也能看到其所发挥的巨大作用［1］。在此基础上，衍生出了能够携带方便和垂直起降，机动能力强并且能稳定飞行的微型筒式共轴双旋翼飞行器（Cylindrical Coaxial Rotor Aircraft，CCRA）［2］。图1所示为CCRA的桨叶折叠之后放在圆筒中的概念描述图，其桨叶折叠之后可以与圆筒的内壁共形，同时能够与机体的圆柱外表面共形，这样飞行器的机体和桨叶均能得到有效的保护。

CCRA 的上下旋翼的旋转方向相反，在飞行过程中产生的扭矩可以相互抵消，从而来保持机体的稳定性，这类飞行器的结构紧凑、具有良好的机动性、良好的悬停稳定性和良好的前进速度能力［3-4］。此外，随着飞行器沿旋翼径向尺寸的减小，飞行器的转动惯量减小，所以它的可控性和机动性也增强了，同时没有尾桨的设计也消除了某些故障隐患［5-6］。

虽然CCRA 有着如上所述许多的优点，但因其小尺寸、紧凑的结构和低空慢速的飞行特性，飞行过程中会遇到以下问题：低雷诺数使空气粘性增强，给计算和实验带来困难；升力系数小，阻力系数大，旋翼的推进效率低，需要更大的飞行动力满足有效载荷的需求；CCRA 机身的振动以及上下旋翼产生的气流干扰等［7］。关于CCRA 空气力学分析的更多信息可以在文献8～11中找到。

旋翼系统的气动设计会直接影响整机性能，因此改善微小型旋翼的气动特性对整机的高效飞行起着关键作用。本文的主要工作是针对CCRA气动模型，设计了一种新型的桨叶，并对这种桨叶构成的旋翼特性进行了理论计算、CFD 仿真和实物测试。结果表明，设计的旋翼具有良好的气动特性，旋翼推进效率高，能提供足够的升力。从工程实际上看，桨叶加工方式简单，造价低，达到了性能优化和成本降低的目标，具有很大的理论和实用价值［12］。

2 空气动力学模型

CCRA 的升力由上下旋翼的反向旋转产生，通过舵机控制上旋翼桨叶使其产生前进方向的分力进而达到对CRS飞行轨迹的控制［13］。

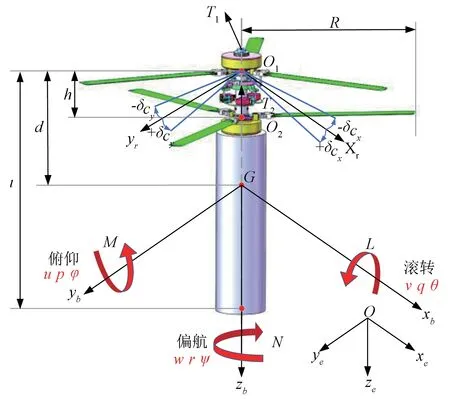
图2 CRS模型示意图Fig.2 Schematic diagram of CRS model

2.1 升力计算模型

上旋翼产生的沿zb的一个垂直力和两个沿xb与yb方向的横向力，随着斜盘入射角（δCx，δCy）的增大，垂直力逐渐变小，横向力逐渐增大。上旋翼产生的推力T1的表达式可以写成如下形式：

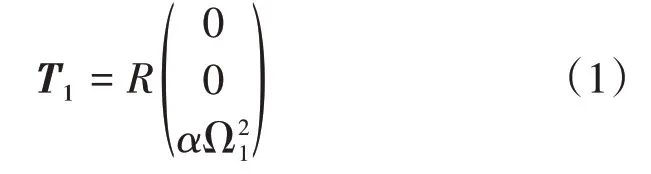
其中

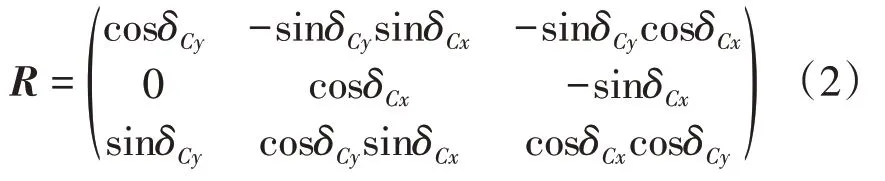
R是机体坐标系{G xbyb zb} 与上旋翼坐标{O1xryr zr} 之间的变换矩阵，α为旋翼的空气动力系数，Ω1为上旋翼转速。从方程（1）和方程（2）可以得到上旋翼产生的推力T1为：

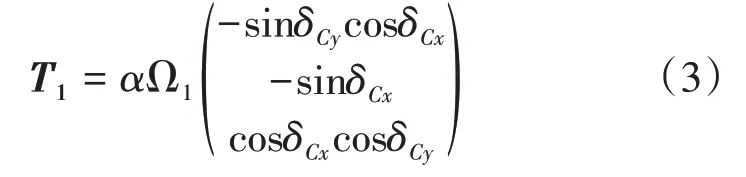
下旋翼产生的推力T2为垂直方向的力，可以写成：

在式（3）和式（4）中出现的空气动力系数α和β是初始推力系数CT1和CT2的函数，与雷诺数Re和空气密度ρ有关，可以写成：

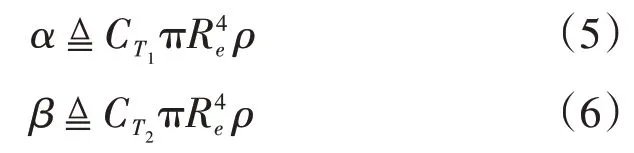
鉴于每个旋翼产生的推力可以通过式（3）和式（4）得到，则沿zb方向总的推力Tzb可以表示为上下两个旋翼产生的沿zb方向的推力之和，实际飞行时上旋翼的下洗流对下旋翼会有较大的影响，取干扰系数为σ，则可以得到：

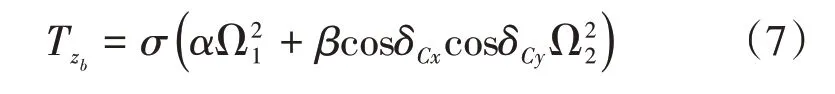
一般情况下，干扰系数σ的取值范围为0.8 ≤σ≤1。

可得出CRS的总的推力为：

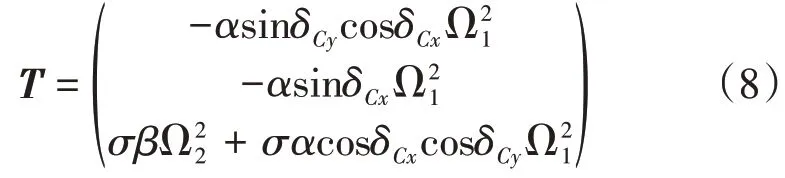
2.2 需用功率计算模型

旋翼需用功率可以分为如下三种形式：（1）克服旋翼旋转气动阻力所产生的型阻功率；（2）为排除旋翼下方空气所消耗的诱阻功率；（3）为克服机身阻力所消耗的废阻功率。

由于CRS 上下旋翼的相互干扰，相同功耗下旋翼的升力大约是上旋翼的86%［14］，在计算需用功率时总功率可以取P= 2Pup×1.219。

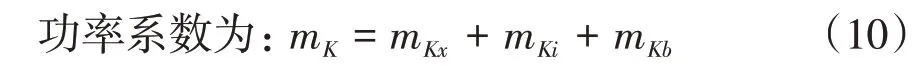
实际需用功率为：

ρ是当地相对大气密度，近似与标准大气密度相等，σ=(Nbc)/(πR)为桨叶实度。为诱导速度。

3 旋翼桨叶的设计

3.1 翼型的设计

考虑到旋翼折叠后与内外表面的配合性，同时保证工程实际能够达到足够的升阻比，进而提供足够的升力，CRS的桨叶采用圆管切割的方式得到，翼型在圆管中的截面示意图如图3所示。

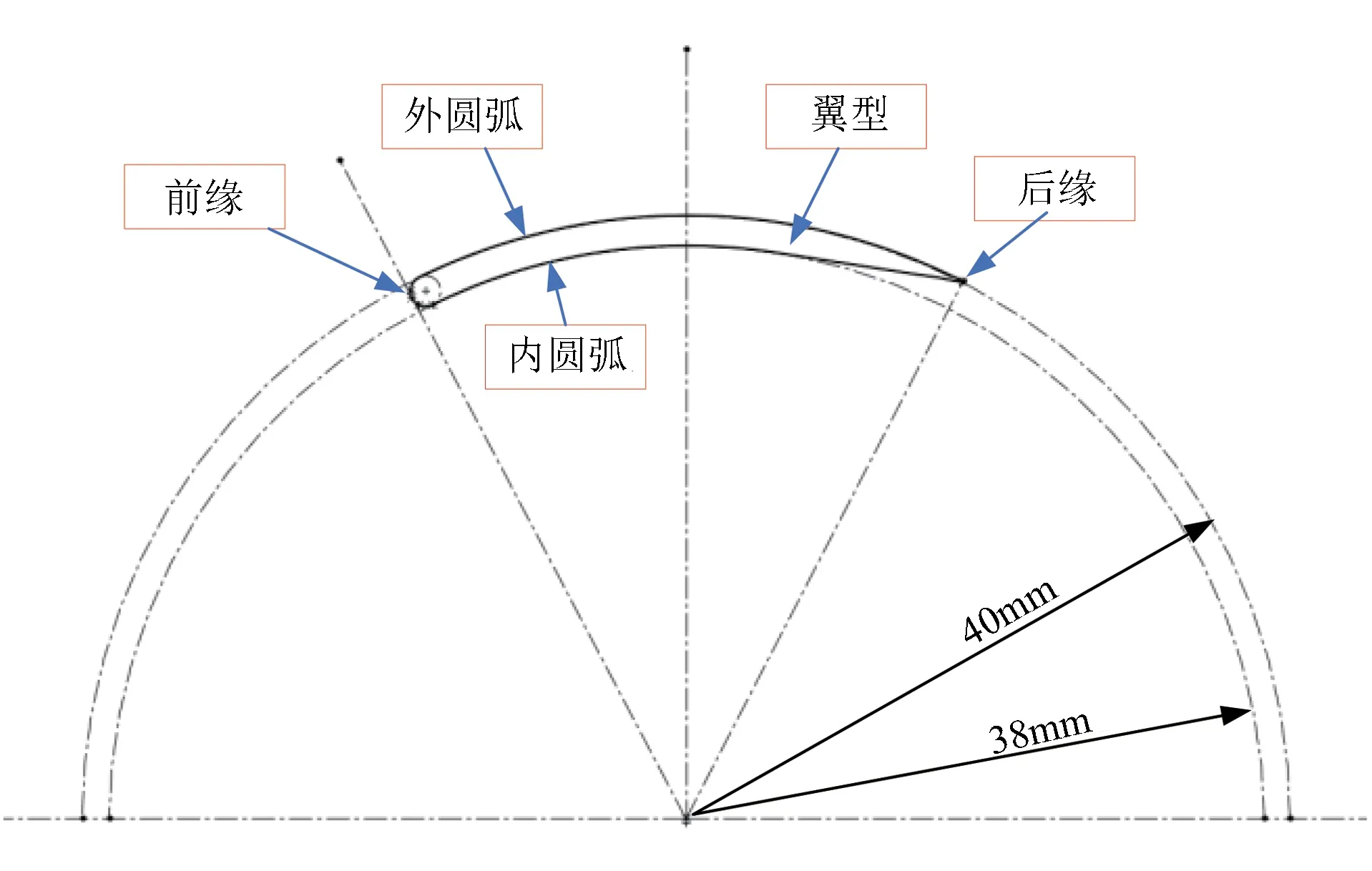
图3 设计翼型截面Fig.3 Design of airfoil cross section

设计的翼型厚度（thickness）为半径的5%，弯曲度（camber measurement）为半径的11.5%，翼型的前缘为半圆形，图4为所设计翼型与标准翼型NACA0012的对比情况［15］。

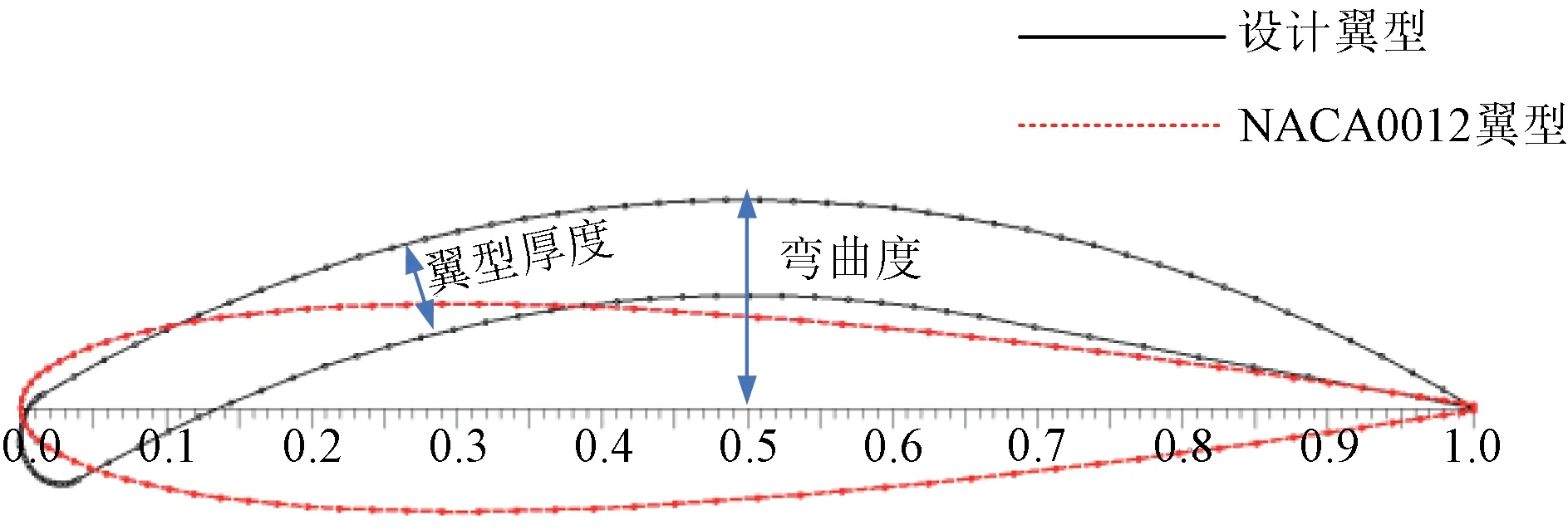
图4 设计翼型与NACA0012翼型对比Fig.4 Comparison of airfoil design and NACA0012 airfoil design

图5和图6为设计翼型与NACA0012 翼型的气动性能对比，环境条件为马赫数为0，NCrit 为9，雷诺数为2×105。不同攻角下升力系数，阻力系数，升阻比对比，从中可以看出，设计翼型相比于常规的NACA0012翼型具有明显的优势，在不同攻角下，新设计旋翼的升力系数有明显增加，同时其阻力系数也会增加。整体来看，其升阻比在攻角为5°、11°左右时比NACA0012 翼型的升阻比大，最佳升阻比出现在攻角11°附近。

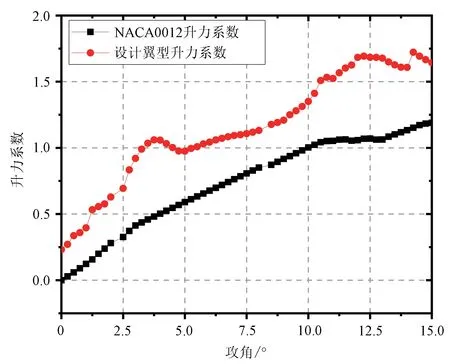
图5 设计翼型与NACA翼型的升力系数对比Fig.5 Comparison of lift coefficient

图6 设计翼型与NACA翼型的升阻比对比Fig.6 Comparison of lift drag ratio

3.2 翼展的设计

桨叶攻角取为11.5°时。不考虑空气密度变化，根据公式（9）-（12），使用MATLAB 来计算需用功率与CRS 旋翼直径之间的关系，在不同直径下，产生相同升力时的需用功率如图7和图8所示。在总重10kg 时，上旋翼在直径0.77m 处所需功率最小，而下旋翼则是在0.74m处所需功率最小，对此，旋翼直径可以选择在0.74m 到0.77m 之间，即单个桨叶长度在320mm到335mm之间为宜，在本次设计中，选取单个桨叶长度为330mm。

3.3 桨叶的优化

由于所设计的桨叶是在圆筒中切割出来的，在翼型优化的时候，只对弦长进行优化，不对扭曲度进行优化，不同截面处的扭曲度均为0［15］。

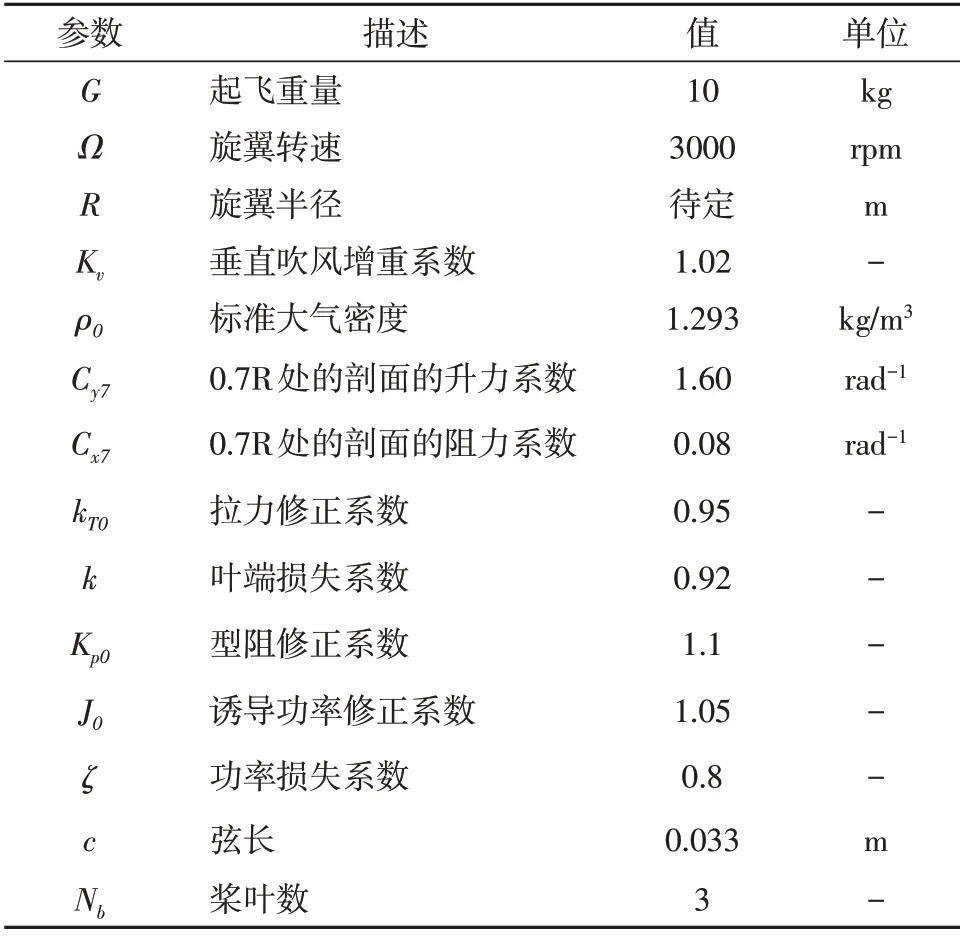
表1 相关物理参数Table1 Related physical paremeters

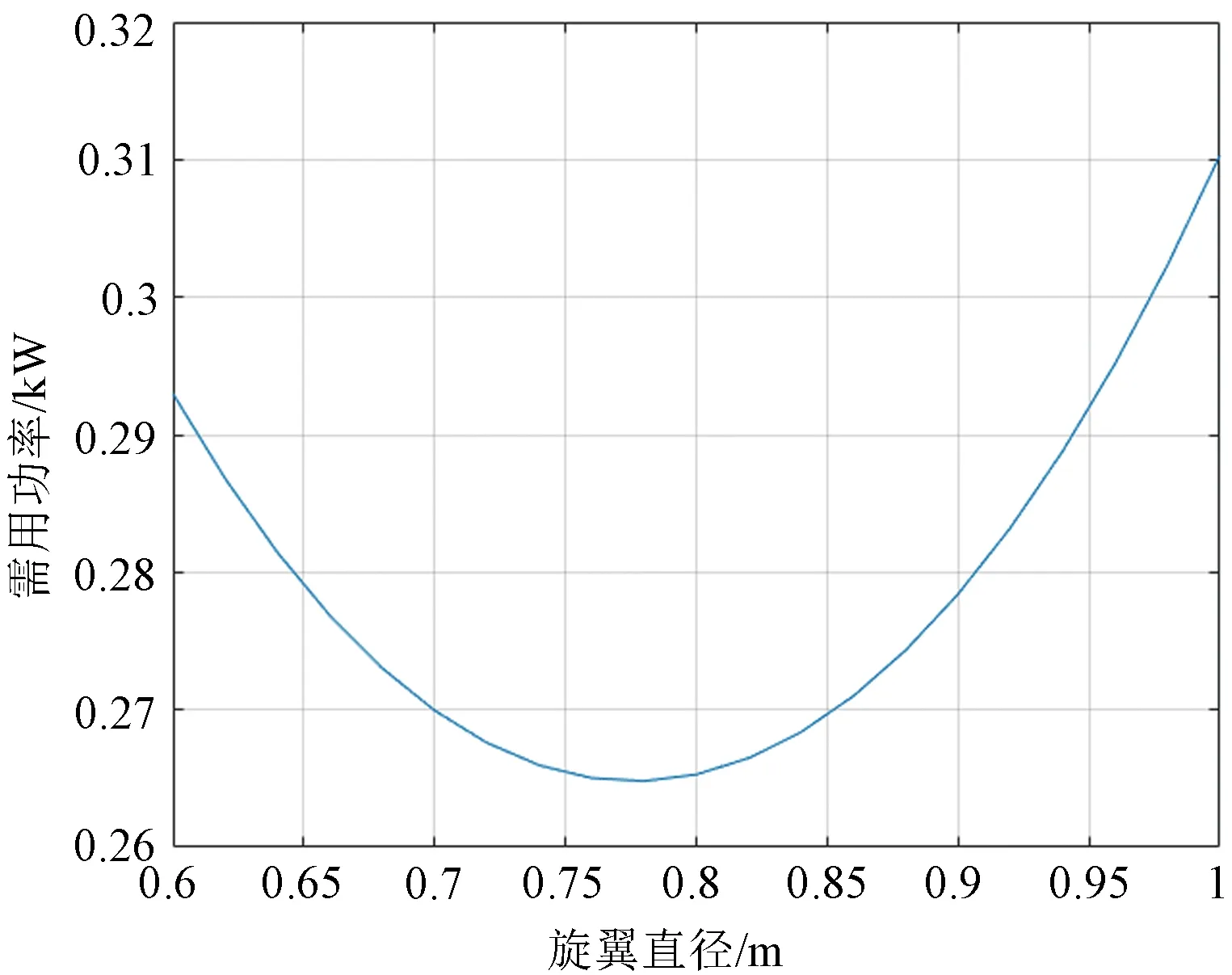
图7 上旋翼直径需用功率曲线Fig.7 Required power curve of rotor diameter

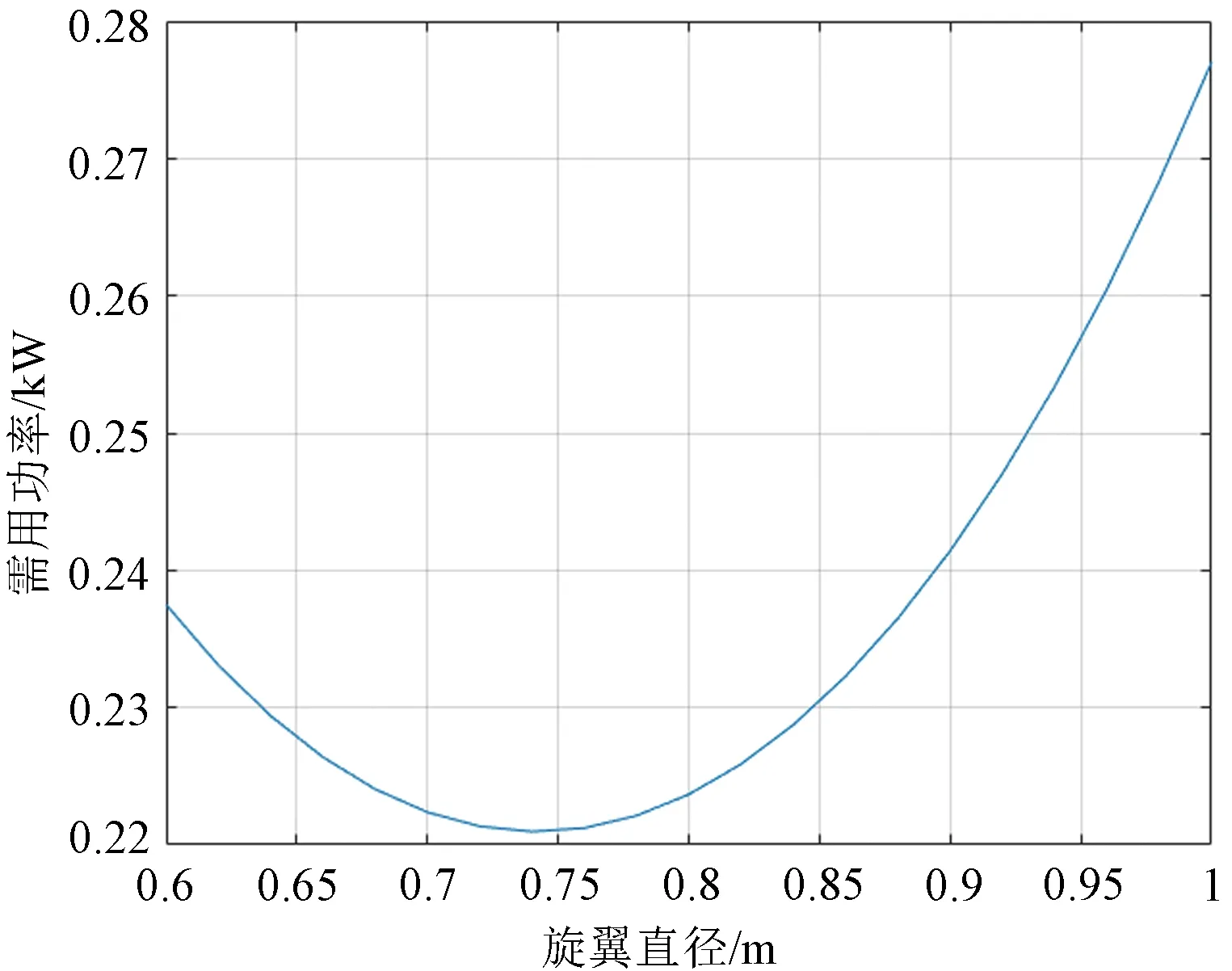
图8 下旋翼直径与需用功率曲线Fig.8 Lower rotor diameter and required power curve

采用Betz 优化方法对弦长进行优化，然后在此基础上进行人工优化。使用Betz 优化方法的理论基础是使旋翼达到最小能量损失［16-17］。

3.3.1 动量与环量方程

V0为轴向速度，va为轴向干涉速度，vt为环向干涉速度，ns为旋翼转速，T为拉力，M为扭矩，r为叶素半径。

根据螺旋桨的动量理论可得出螺旋桨在半径r处叶素的拉力与转矩：

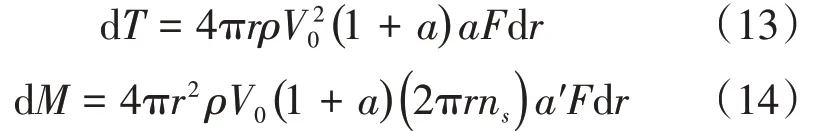
其中，a为轴向干涉系数，定义为为轴向干涉系数，定义为为速度修正系数，在这里可以取F= 1。

根据叶素理论以及图9可知，叶素翼型所受到的升力为：

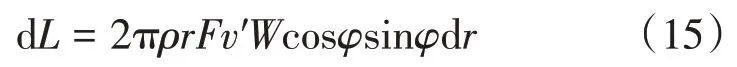
叶素的拉力dT与转矩dM为：

其中γ为阻升角，tanγ=CD/CL。

3.3.2 最小能量损失条件

令使用片条理论和叶素理论得到的拉力与扭矩相等，可以得出轴向干涉系数a与环向干涉系数a′分别为：

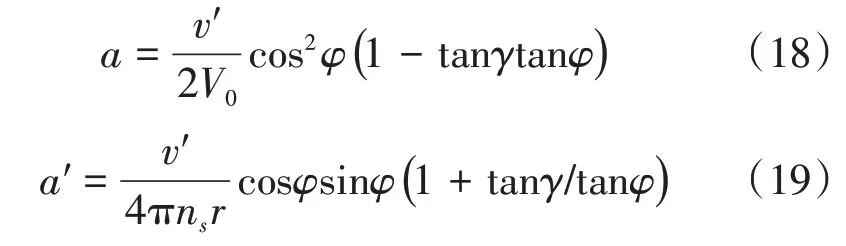
因此，当飞行器状态一定时，v′为常数，即能量损失最小条件为v′是常数。

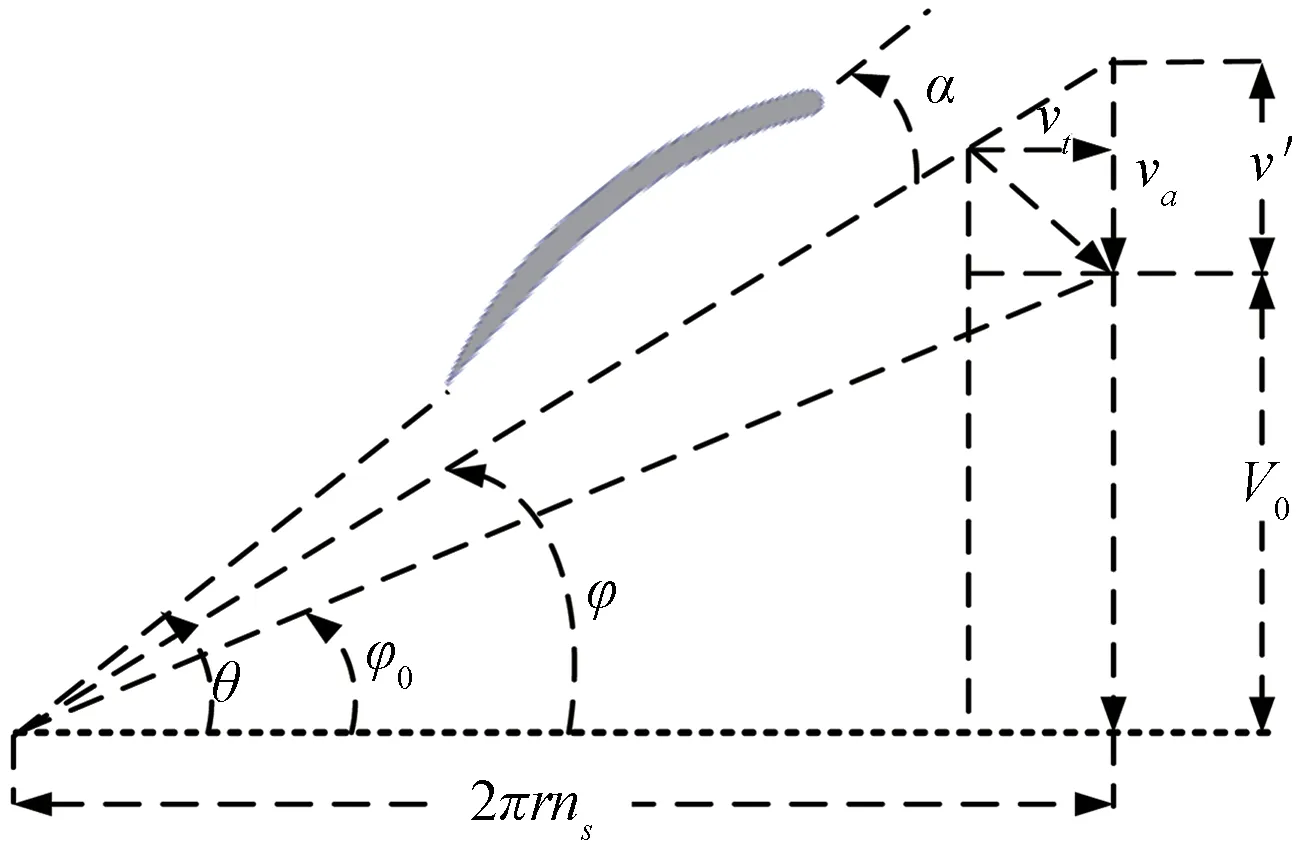
图9 叶素速度三角形Fig.9 Velocity triangle of blead element

基于以上的理论推导，可以对翼型进行迭代优化。优化的结果如图10所示。

图10 弦长优化Fig.10 Chord length optimization

图10中黑色的线为初步预定的弦长，每个截面的弦长初始值为33mm，红色线为使用Betz 方法优化后各个截面的弦长，可以看出靠近根部的相邻截面间的弦长变化较大，这一部分接近于圆弧形，靠近翼尖部分基本上为线性变化，这样的桨叶外形只需要在圆筒上进行简单的切割便可以得到，不同截面的具体弦长如上图曲线Betz 优化弦长所示。

4 共轴双旋翼飞行器气动仿真与实物验证

4.1 网格划分与边界条件设置

由于CCRA 上下旋翼高速反向旋转，在模拟实际飞行状态下的流场情况时，旋翼流场附近的空气流动对旋翼旋转影响较大，特别是上下旋翼形成的气流之间的相互影响。在使用CFD方法来对CCRA的流场进行分析时，可以采用滑移网格的方法单独生成以下几部分的网格：上旋翼网格、下旋翼网格、旋转域网格和计算域网格，然后将它们进行嵌套，通过网格间相对运动实现桨叶运动［18-19］。

考虑到计算速度以及准确度，同时也要考虑到旋翼旋转过程中空气黏性的影响，选用Navier-Stokes方程作为流场控制方程，选择SST k-omega二阶湍流模型来处理流场中的气流流动。使用压力耦合方程组的半隐式方法SIMPLE算法来计算旋翼流场的不可压流动，使用Standard 格式的压强插值方法，能量方程均采用二阶迎风。桨叶表面选用壁面边界条件，空气域流场为静止区域，上下旋转域为反向旋转两个流动区域，其旋转速度分别取上下旋翼的转速，利用上下旋转域的转动来模拟双旋翼的转动。从文献［2］可知，共轴双旋翼的上下旋翼转速相同时，两个旋翼之间的气动干扰小。在实验测试时，取上下旋翼转速一致。最终生成的网格总数约500万，整个项目的网格划分结果如图11所示。

图11 网格划分图Fig.11 Grid partition diagram

4.2 半实物仿真

半实物仿真的测试装置按照图12左侧所示，依次可分为旋翼部分、扭矩拉力测试组、支架、压力测试组，支架高度大于1.5m 是为了减弱地面效应。图12右侧为具体测试情况图，接上电源后传动机构会带动旋翼旋转，通过对旋翼贴片的方式记录旋翼转速，通过传感器来获取不同情况下产生的升力，利用供电电源的电流电压可以计算出实际功率。

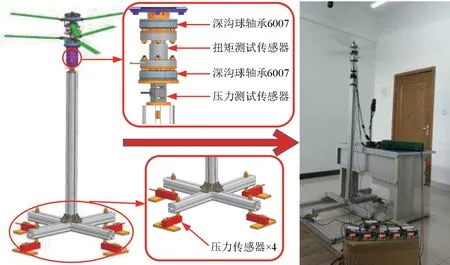
图12 半实物仿真测试装置及测试过程Fig.12 Experiment device and testing process

4.3 实验数据分析

在图13中，虚线表示用CFD 仿真得到的数据，实线表示用半实物仿真得到的数据，两者在误差允许的范围内相吻合，表明了数据的可靠性。图中黑线表示设计的旋翼，红线表示NACA0012 翼型构成的旋翼（翼展为330mm，不同截面处的扭曲度均为0，弦长为定值33mm），明显可以看出设计翼型构成的旋翼在各种转速情况下，提供的升力大于NACA0012翼型构成的旋翼，并且转速越大，两者提供的升力差值越大。设计的旋翼在3000rpm时已经能够提供接近10kg升力，满足设计要求。

图13 转速与升力的关系图Fig.13 Relationship between rotation speed and lift

在图14中，虚线为通过理论计算得到的需用功率，实线表示用半实物仿真得到的实际需用功率，半实物仿真时的需用功率整体比理论计算值大，表明实际的功率损耗比预计的更大，可能存在较大的传动损失和一些附件的功率消耗。对比图中的红线与黑线，可以看出不同转速下优化旋翼均比NACA-0012旋翼的需用功率低，以转速3000rpm为例，此时NACA0012 旋翼的实际需用功率达到了1153.6W，其效率为7.52g/W，而新设计翼型的旋翼在相同情况下实际需用功率只有984.3W，效率为10.25g/W，可见新设计的旋翼在功率消耗上具有很大优势。

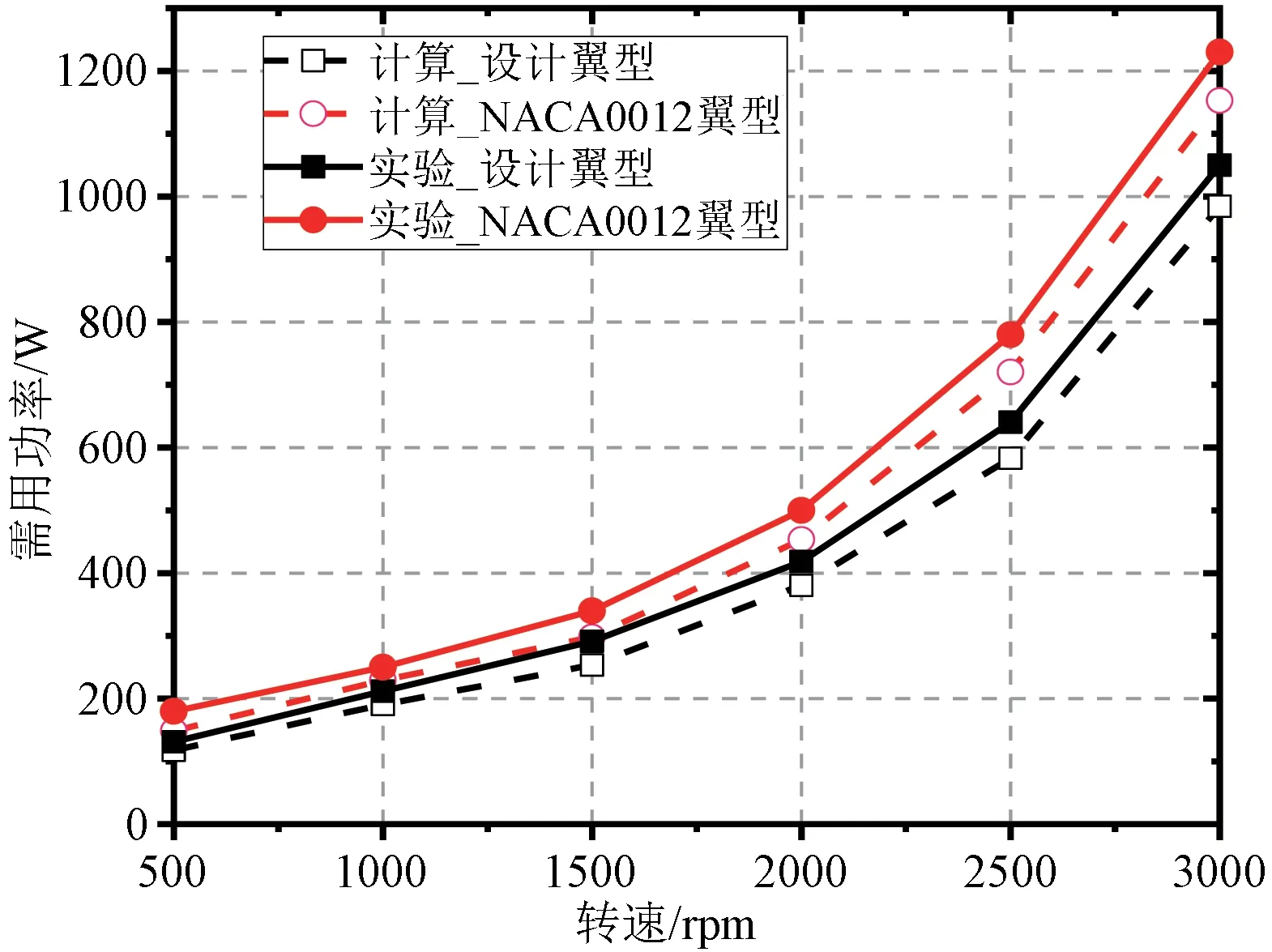
图14 转速与功率的关系图Fig.14 Relationship between speed and power

5 结 论

本文在CCRA 概念的基础上，建立了CCRA 的空气动力学模型用于对升力的计算，然后开始设计适用于CCRA的圆弧形旋翼，经过翼型设计、翼展设计、弦长优化，得到一种新的旋翼模型，最后通过CFD 流体仿真与半实物仿真进行了验证。通过与经典的NACA0012 旋翼对比，新设计的圆弧形旋翼具有明显的优势，在相同转速下，新设计的旋翼需用功率更小，产生的推力更大，能量转换率更高，更能满足低功耗、高负载、高稳定性、低成本、结构简单可靠的要求［20］。

本文的设计思路与方法将对类似的翼型设计具有很强的指导意义，在初步满足设计要求的基础上，还可以对所设计的圆弧翼进一步的进行优化，探究旋翼设计与整个机体的气动稳定性之间的关系。