地月L2点空间站转移轨道设计与特性分析

曹鹏飞，贺波勇，刘景勇，彭祺擘

(1.北京航天飞行控制中心，北京100094；2.西安卫星测控中心宇航动力学国家重点实验室，西安710043；3.中国航天员科研训练中心，北京100094)

1 引言

地月L2点(以下简称LL2点)位于月球背面约6.5×104km处，在月球探测中具有重要作用。早在Apollo时代，Farquhar就发现LL2点附近存在大量三维周期轨道，即Halo轨道[1]，并首次提出了Halo轨道空间站的概念[2-3]，指出与环月轨道空间站相比，LL2点Halo轨道空间站在月球探测方面更有优势，包括与月面站有更长的通信时长、与地球通信无遮挡、兼顾月球背面通信和运营方式相对自主等[4]。但由于资金等诸多原因，该方案未被实施。1978年，美国成功发射了世界首颗平动点探测器ISEE-3[5]，在国际上掀起了一轮平动点转移轨道研究热潮。Gomez等[6]通过引入动力系统理论，发现共线平动点附近存在大量无动力飞行的不变流形。Parker等[7]基于不变流形，通过大量仿真数据研究了从近地停泊轨道(Low Earth Orbit，LEO)出发到达LL2点Halo轨道的转移轨道特性，发现在月球附近插入不变流形，可同时节省一定的燃料和时间成本。Gordon[8]基于月球借力与不变流形，通过采用改进的微分修正方法设计了LEO出发到达LL2点Halo轨道的转移轨道。Li等[9]在Gordon的研究基础上，提出了基于月球借力的LL2点Halo轨道三脉冲转移策略，进一步降低了燃料消耗。张景瑞等[10]基于遗传算法与微分修正算法结合的混合优化技术，研究了不同月球借力约束下的LL2点Halo轨道转移轨道设计问题。

上述学者对基于不变流形与月球借力的LL2点间接转移轨道设计方法做了比较深入的研究，但对该类转移轨道的一般特性规律研究尚不充分。本文以未来LL2点Halo轨道空间站的货物补给任务为背景，结合解析初值猜想和局部梯度优化，提出一种串行间接转移轨道优化方法，并在此基础上，通过大量仿真算例研究不变流形插入相位、月球借力高度以及Halo轨道幅值等参数对转移轨道燃料消耗的影响特性。以期为未来LL2点Halo轨道低能转移任务轨道方案制定提供参考。

2 动力学模型

2.1 圆型限制性三体问题

本文所选用的动力学模型为圆型限制性三体问题(Circular Restricted Three Body Problem，CR3BP)模型，即在一个三体系统中，假设质量分别为M1和M2的两大天体P1和P2，绕其公共质心做匀速圆周运动，研究质量为m的第三体P在P1和P2引力下的运动规律。三个天体的质量关系为M1＞M2≫m，即P对P1和P2的运动影响可忽略不计[4]。

CR3BP中常用的坐标系为质心会合坐标系[4]，其原点位于P1和P2的公共质心O，x轴由P1指向P2，z轴指向系统角动量矢量方向，y轴与其他两轴构成右手坐标系。引入归一化单位，长度单位为P1和P2质心间的距离，质量单位为M1、M2之和，P1和P2的相对运动周期为2π。 引入质量比μ如式(1)：

在归一化单位下，第三体P在会合坐标系中的动力学方程[4]如式(2)：

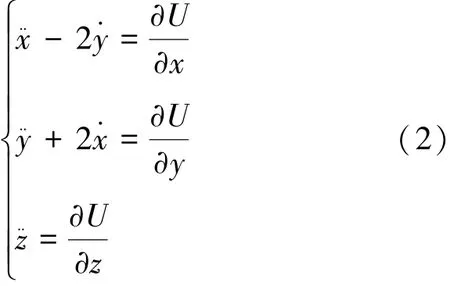
其中，U为与位置相关的伪势能函数，表达式为式(3)：

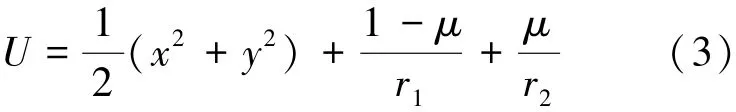
式中，r1和r2分别为P到P1和P2的距离，表达式如式(4)、(5)：

2.2 Halo轨道及不变流形

Halo轨道是共线平动点附近的三维周期轨道，在平动点任务中被广泛应用。CR3BP会合坐标系下，Halo轨道关于xz面对称，与xz面交于两点，通常取其中距离x轴较远的点与x轴的距离作为表征Halo轨道大小的参数，称之为法向幅值Az，计算过程可参考文献[4]。

不变流形是与Halo轨道自然相衔接的空间轨道，分为稳定流形与不稳定流形，在低成本深空轨道设计中被广泛应用。将Halo轨道离散为不动点，并求解不动点处的单值矩阵Φ(T，0)，即一个Halo轨道周期后的状态转移矩阵。每一不动点对应的Φ(T，0)矩阵均存在三对乘积为1的特征值：λu＞1为不稳定特征值，对应不稳定特征向量Vu；λs＜1为稳定特征值，对应稳定特征向量Vs；一对互为共轭的复数特征值和一对值为1的特征值。在不动点处施加一个小扰动即可得到不变流形积分初值。

对于不稳定流形，其积分初值Xu0如式(6)：

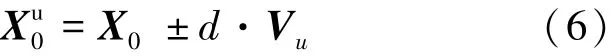
对于稳定流形，其积分初值Xs0如式(7)：

式中：X0为不动点状态量；d为扰动变量。对于地月系统，为了满足方程线性，d一般取30～70 km。

2.3 LEO-LL2 Halo间接转移轨道方案

本文针对LEO出发达到LL2点空间站的货物补给运输任务，综合不变流形与月球借力两种节省燃料方式，提出LEO-LL2 Halo间接转移轨道方案，如图1所示。

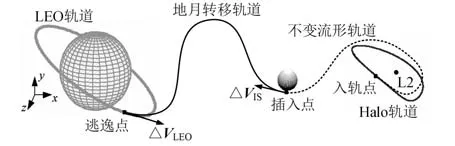
图1 LEO-LL2 Halo间接转移轨道示意图Fig.1 Schematic diagram of LEO-LL2 Halo indirect transfer trajectory

由图1可知：LEO-LL2 Halo间接转移轨道共包括2段，分别是地月转移轨道段和不变流形轨道段，二者在月球附近实现拼接；整个转移过程共需要2次脉冲机动，第一次机动的位置为近地LEO，作用是使航天器逃离LEO进入地月转移轨道，第二次机动的位置为月球附近，作用是使航天器插入稳定流形。

3 LEO-LL2 Halo间接转移轨道设计

本节将CR3BP下LEO-LL2 Halo间接转移轨道设计问题，转换为有约束非线性规划求解问题。建立优化模型，并在此基础上，提出一种解析初值猜想与局部梯度优化相结合的求解策略。

3.1 轨道优化模型

下面从设计变量、约束条件和目标函数三方面介绍其优化模型。

设计变量为逃逸点高度hE、逃逸点切向逃逸脉冲ΔVLEO、稳定流形(可由近月点高度hS确定)、地月转移段转移时间TES、稳定流形插入位置XIS，稳定流形插入脉冲ΔVIS以及Halo轨道幅值Az。设计变量均已知时，在CR3BP下可唯一确定一条LEO-LL2 Halo间接转移轨道。其中，hE＝hLEO，由发射系统确定；hS根据测控系统精度确定；Az由任务目标给定。因此，一条LEO-LL2 Halo间接转移轨道可由式(8)所示的4元素确定：

约束条件主要考虑转移时间和近地点高度约束。参照嫦娥四号中继星任务[11]，本文将工程与轨道约束简化为式(9)：

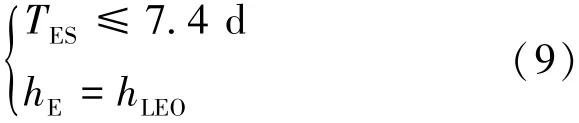
由于空间站货物补给任务对转移时间的要求并不高，本节在轨道设计时弱化了时间约束，以总燃料消耗为优化目标，即目标函数为式(10)：

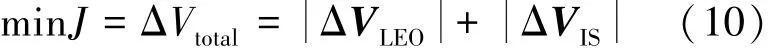
3.2 求解策略

针对上述优化模型求解问题，提出一种解析初值猜想与局部梯度优化相结合的求解策略，具体流程如图2所示。

1)根据火箭运载能力与任务目标，确定LEO轨道高度hLEO、稳定流形近月点高度hS和目标Halo轨道。

2)计算目标流形轨道。首先，将Halo轨道按时间等间距离散成360份，并按时间顺序对离散点进行编号n＝1～360，如图3所示；其次，计算360个离散点对应的稳定流形，并选出近月点高度与hS一致的稳定流形，作为目标流形轨道。

图4给出了满足不同近月点高度约束的稳定流形，由图可知，当近月点高度给定时，将存在两条稳定流形与之对应，分别称之为“A型”和“B型”稳定流形。其中，B型稳定流形在绕月后径直奔向Halo轨道，因此不适用于从LEO出发到达Halo轨道的转移任务。本文选用A型稳定流形轨道作为目标流形轨道。

定义目标流形轨道上位于月球附近的积分点为插入点，并将其相对月球的相位记为φ。如图5所示，φ与插入点位置XIS构成一一对应关系。

图2 基于CR3BP的LEO-LL2 Halo转移轨道求解流程图Fig.2 Flow chart of solution of LEO-LL2 Halo transfer trajectory based on CR3BP

图3 Halo轨道上360个离散点分布图Fig.3 Distribution map of the 360 discrete points on Halo orbit

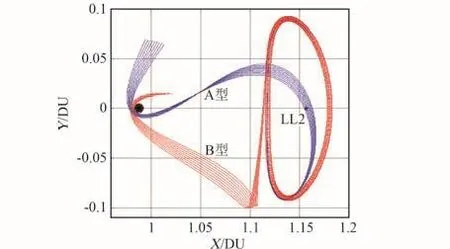
图4 满足近月点高度约束的稳定流形Fig.4 Stable manifold orbits satisfying the attitude constraint at perilune

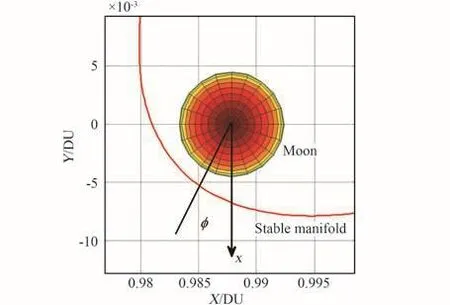
图5 不变流形插入点相位定义Fig.5 Definition of phase of the insertion point on invariant manifold orbit

3)基于时间逆向积分求解思路，通过采用SQP算法优化一条从LEO出发到达φ＝90°插入点的地月转移轨道。优化变量如式(11)所示：

迭代初值如式(12)所示：

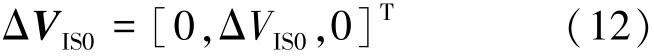
其中，ΔVIS0由二体模型霍曼转移理论[12]给出，计算公式如式(13)：

式中，uE为地球引力常数；r1为LEO轨道半长轴；r2为φ＝90°插入点的地心距。约束条件见式(9)，当约束条件满足时，通过活力公式即可解析计算出ΔVLEO。 优化目标为总燃料消耗最少，目标函数见式(10)。优化得到的φ＝90°插入点对应的最优插入脉冲记为对应的入轨点切向逃逸脉冲大小记为。

4)通过采用数值延拓策略，计算从LEO出发到达其他插入点的地月转移轨道。由于步骤3已经得到从LEO出发到达φ＝90°插入点的地月转移轨道，在求解LEO出发到达φ＝91°或φ＝89°插入点的地月转移轨道时，将步骤3中优化变量初值设为ΔVφ＝90LEO即可。依次递推，可计算出LEO出发到达任意插入点的地月转移轨道。

5)分析插入点相位与总速度增量之间的关系，即可得到燃料最优的LEO-LL2 Halo间接转移轨道。

3.3 算例验证

LEO-LL2 Halo间接转移轨道设计实例参数及约束配置如下：LEO高度hLEO＝185 km；目标流形轨道近月点高度hS＝200 km；地月转移段飞行时间TES≤ 7.4 d；Halo轨道幅值Az＝10000 km，为LL2点南向Halo轨道。

通过采用3.2节的求解策略，计算满足上述约束且燃料最优的LEO-LL2 Halo间接转移轨道，计算得到的轨道飞行轨迹如图6所示，相应的轨道参数见表1。计算在计算机CPU为2.67 GHz的MATLAB环境下进行，单条轨道的计算时长不超过30 s。因此，利用该方法进行LEO-LL2 Halo间接转移轨道设计时，收敛速度很快，适合用于大规模的轨道特性分析。

图6 hS＝200 km的目标流形轨道对应的LEO-LL2 Halo间接转移轨道Fig.6 LEO-LL2 Halo indirect transfer trajectory corresponding to the target manifold orbit with 200 km perilune attitude

表1 燃料消耗最优的LEO-LL2 Halo间接转移轨道参数Table 1 Parameters of LEO-(LL2)Halo indirect transfer trajectory with optimal fuel consumption

4 LEO-LL2 Halo间接转移轨道特性分析

在任务设计阶段，工程人员往往对单条轨道参数并不关心，而是更加注重这一类轨道的一般规律。本节在3.3节算例的基础上，通过仿真实验对满足约束的LEO-LL2 Halo间接转移轨道特性进行分析。

4.1 稳定流形插入点相位影响分析

针对插入点相位和转移燃料消耗之间的关系，以3.3节算例为基础，目标流形轨道插入点相位φ设为0～180°，其余参数设置保持不变。采用3.2节求解策略，逐条计算出从LEO出发达到φ＝0～180°插入点的地月转移轨道，得到插入点相位φ与总速度增量ΔVtotal的关系，如图7所示。由图可知：①插入点相位φ对转移速度增量ΔVtotal的影响较大，当φ≈120°时，ΔVtotal取极小值，约为3.4818 km/s。 ②当φ＜120°时，φ越小，ΔVtotal越大。产生上述现象的原因：当φ减小时，插入点与目标流形近月点之间的间距将增大，继而将导致月球借力效果变差，ΔVtotal增加(图5)。③当φ＞120°时，φ增大，ΔVtotal将略增大。由图4可知，这一点是由目标流形的“走向”引起的。

4.2 稳定流形近月点高度影响分析

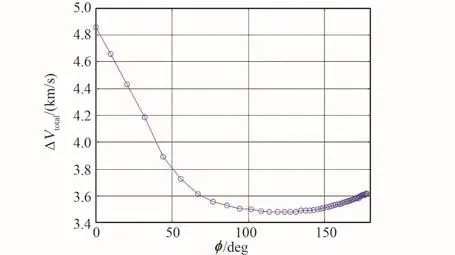
图7 插入点相位与转移总速度增量的关系Fig.7 Relationship between the phase of insertion point and the total velocity increment of transfer consumption

针对目标流形近月点高度和转移所需的最小燃料消耗之间的关系，以3.3节算例为基础，目标流形轨道近月点高度hS设为100～5000 km，其余参数设置保持不变。选出近月点高度hS为0～5000 km的A型目标稳定流形族如图8所示。采用3.2节求解策略，逐条计算出从LEO出发达到所有目标稳定流形的燃料最优的地月转移轨道。得到近月点高度与总速度增量的关系如图9所示。

由图9可知：目标流形近月点高度hS对总速度增量ΔVtotal有一定影响，但整体影响不大；当hS取0～1300 km时，ΔVtotal相对较小且波动变化不大；当hS＞1300 km时，hS越大，转移所需的速度增量越多，该结论与文献[9]中借力飞行理论相吻合。

4.3 Halo轨道法向幅值影响分析

图8 满足近月点高度约束的稳定流形Fig.8 Stable manifold orbits satisfying the attitude constraint at perilune

图9 目标流形轨道近月点高度与转移总脉冲关系Fig.9 Relationship between attitude of perilune of the target manifold orbit and the total velocity increment of transfer consumption

针对Halo轨道法向幅值和转移所需的最小燃料消耗之间的关系，仍以3.3节算例为基础，Halo轨道幅值Az＝5000、10000、……、30000 km，目标流形轨道插入点相位φ＝120°，近月点高度hS＝200 km，其余参数设置保持不变。采用3.2节求解策略，逐条计算出从LEO出发到达不同Halo轨道的燃料最优LEO-LL2 Halo间接转移轨道，得到Halo轨道幅值Az与总速度增量ΔVtotal的关系如图10所示。

由图10可知，Halo轨道的幅值Az对转移所需总速度增量的影响较为显著，Az越大，越大，反之亦然。该现象可通过目标流形轨道近月点时刻的速度矢量与白道面的夹角β解释。不同Az的Halo轨道对应的目标流形轨道如图11所示。

图10 Halo轨道法向幅值与总脉冲消耗关系Fig.10 Relationship between the normal amplitude of Halo orbit and the total velocity increment of transfer consumption

由图11可知：对于小幅值(如Az＝5000 km)的Halo轨道，β比较小，月球借力效果较为显著；而对于较大幅值(如Az＝30 000 km)的Halo轨道，β则比较大，月球借力效果不佳，导致转移所需的燃料消耗较多。因此，LEO-LL2 Halo间接转移轨道方案更适用于从LEO出发到达小幅值Halo轨道的转移任务。

5 结论

本文研究了不变流形和月球借力相结合的间接转移轨道设计方法及轨道参数特性。建立的LEO-LL2 Halo间接转移轨道优化模型，提出的解析初值搜索和局部梯度优化相结合的串行优化求解方法，通过算例得到了验证。仿真实验表明，不变流形插入相位和Halo轨道幅值对间接转移轨道燃料消耗的影响比较大，而月球借力高度的影响则比较小。研究结论可为未来LL2点低能转移任务的轨道方案制定提供参考。

图11 不同幅值Halo轨道对应的目标流形的三维图Fig.11 The 3D maps of target manifold orbits corresponding to the Halo orbits with different Az