巧解静力学中动态平衡

赵伟敏 段琼

摘 要：静力学动态平衡问题的讨论，作为考察中学生物理思维、分析能力和运用数学知识解决物理问题的很好素材，而广受高中物理教师和高考命题专家的青睐。也因为该问题一般比较繁琐处理难度大，而成为高中生学习物理的一个痛点。因此，我将解决静力学中的动态平衡问题的技巧性方法做了以下梳理。

关键词：静力学 共点力 动态平衡

三力共点平衡的动态分析，主要考察因某个力变化而引起其它力变化的讨论。通常采用构造函数讨论单调性，一般都比较繁琐，同时运算量也很大。正是这样的原因，我们可以借鉴力的图示，通过用线段长短来表示力的大小，从而把物理上的静力学问题转化为较简单的平面几何问题，充分利用平面几何的直观性，进行问题的解答，回避复杂的代数运算。

下面我将给出常见的三种利用几何方法讨论动态平衡的方法。

一、动态三角形法

三力中，有一个力是恒力，另一个力方向不变，讨论这两个变力的具体变化关系，可采用动态三角形方法进行讨论。

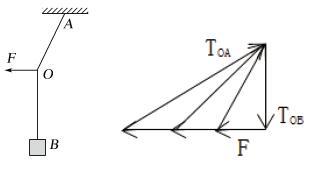
[例1] （2016全国卷Ⅱ）质量为m的物体用轻绳AB悬挂于天花板上。用水平向左的力F缓慢拉动绳的中点O，如圖所示。用T表示绳OA段拉力的大小，在O点向左移动的过程中（ ）

A.F逐渐变大，T逐渐变大B.F逐渐变大，T逐渐变小

C.F逐渐变小，T逐渐变大D.F逐渐变小，T逐渐变小

解析：对绳结O受力分析，OB绳拉力等于物块B的重力是一个恒力，水平拉力F方向保持不变，绳OA拉力在变，但节点O受三力共点平衡，可构造出下面的动态三角形由图可得，选A

二、相似三角形法

在三力平衡问题中，如果有一个力是恒力，另外两个力方向都变化，且题目给出了空间几何关系，并且关系中有一个边不变，一个边长短不变时，可采用力的矢量三角形与空间几何三角形相似，利用相似三角形对应边成比例进行计算。

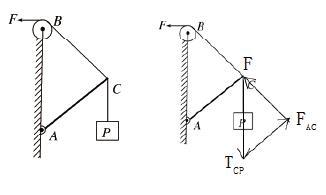
[例2]如图是一个简易起吊设施的示意图，AC是质量不计的撑杆，A端与竖直墙用铰链连接，一滑轮固定在A点正上方，C端吊一重物。现施加一拉力F缓慢将重物P向上拉，在AC杆达到竖直前（ ）

A.BC绳中的拉力FT越来越大      B.BC绳中的拉力FT越来越小

C.AC杆中的支撑力FN越来越大  D.AC杆中的支撑力FN越来越小

解析：对绳结C受力分析，CP绳拉力等于物块P的重力是一个恒力，铰接杆AC只能提供支持力，绳BC拉力沿绳，结点C受三个力，除CP绳拉力为恒力外，另两力均不能确定，但是AB距离不变，杆长AC不变，可有相似三角形如图，由力的矢量三角形与几何三角形ACB相似有，所以选B。

三、辅助圆法

在圆中，同一段弦所对圆周角相等（如图弦AB）。

我们可以利用圆的这一定理来解决静力学中这样一类动态分析问题：一个力是恒力，另外两个力夹角不变的三力动态平衡问题。

[例3]（多选）（2017全国卷Ⅰ）如图，柔软轻绳ON的一端O固定，其中间某点M拴一重物，用手拉住绳的另一端N，初始时，OM竖直且MN被拉直，OM与MN之间的夹角为α（α>）。现将重物向右上方缓慢拉起，并保持夹角α不变。在OM由竖直被拉到水平的过程

中（）

A.MN上的张力逐渐增大B.MN上的张力先增大后减小

C.OM上的张力逐渐增大D.OM上的张力先增大后减小

解析：轻绳只能提供沿绳拉力，而题目要求两绳夹角α不变，对重物

M受力分析，其受三个力，其中重力是恒力，另外两个沿绳拉力，夹角不变，

画出M受力分析图，θ+α=π由图可知，选AD

以上为解决三力共点平衡的动态分析常用三种几何方法，不同方法对应不同动态特点，而根据不同特点，构造相应几何环境，采用平面几何的方法，可以直观简洁地给出变力的变化规律，回避了繁琐的数学分析和运算。以上各题也可采用纯粹的数学计算，有兴趣的读者可自行完成。