弹性管束湿模态频率变化对传热特性影响分析

俞逸杰，宋继伟，柴小明，侯兰雅，程 林

(山东大学 热科学与工程研究中心, 济南 250061)

弹性管束换热器利用流体诱导管束振动强化传热，并通过系统阻尼使管束自由端的振动得到有效控制[1]。

弹性管束的振动特性直接影响换热器的性能[2]，一直以来，其振幅和振动响应是各学者研究的焦点[3-4]，但是随着对固有频率的深入研究[5-7]，可以发现振动元件的固有频率也是重要的设计参数。事实上，当弹性管束处于一定的流体域时，其湿模态频率[8-9]通常与其固有频率存在差别，并且随着流体物性及运行工况的改变而变化，在设计中忽略这种差异会对换热器的实际运行效果产生影响。为表征换热管外掠流体对其振动特性的影响，换热器设计中会引入附加质量[10]的概念。

本文通过对弹性管束附加质量系数的分析，研究了流体黏度、流速对弹性管束湿模态振动频率及其传热性能的影响。

1 理论分析

弹性管束由四根弯曲半径不同的弹性管以及位于管端的配重块装配而成，如图1所示。其中，Ⅰ、Ⅱ两处为固定端面，Ⅲ、Ⅳ两处为自由端。

在振动计算中，弹性元件的质量是一个重要参数，

图1 弹性换热管束

在涉及弹性元件外部流体动力质量的计算时，由于元件的振动，会使外部流体随振动而发生位移，导致元件表面压力分布发生变化，并以惯性力的形式作用在元件表面。

由于流体黏性的影响，当元件在黏性流体中作加速度运动时，流体力的影响非常明显，使元件增加一个附加质量，若将本文研究对象的振动情况简化为垂直于元件初始平面的面外振动，即沿图1所示的轴线方向振动，受力情况可用式(1)表示[11]。

(1)

式中:F为弹性元件受到的合力，由元件结构力和流体黏性阻力两部分组成，ma是附加的流体动力质量，x是位移，Cv是量纲为kg·m的黏性阻力系数。

对于弹性元件沿自身轴线方向振动时，Cv可以表达为振动频率、半径和流体黏度的函数[11]：

(2)

(3)

式中:ω为振动的圆频率，ω=2πf,f为模态频率；r为元件弯管处的外径，v为黏度系数。

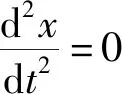
(4)

由式(4)可知，当外掠流场的流速一定的情况下，流体黏度的增加或减小会使弹性元件模态频率f减小或增大。

(5)

由式(5)可知，当外掠流体速度为0时，F结构=0此时，弹性元件处于结构的平衡位置(无形变)；当外掠流体速度不为0时，F结构≠0。因此，弹性元件偏离结构的平衡位置，即流体给弹性元件施加了一个张力，且流体速度越大，施加的张力越大，其模态频率会相应增大。

以上是对弹性元件湿模态频率随外部流场的流体黏度和来流速度变化的情况进行了定性分析，而元件的湿模态频率同时也可通过附加质量得到体现。

通常，流体动力质量ma可以由附加质量系数CM表示，CM为无量纲数，定义如式(6)所示。

(6)

弹性元件沿自身轴线方向振动时，CM可以表达为如下形式：

(7)

式中:Γ的表达式如式(3)所示，是ω、r和v的函数。对于黏度v=0，浮升力F浮=0的理想流体，由式(7)可知，元件的附加质量系数CM=1；并且，由式(2)可知，黏性阻力系数Cv=0。通过数值计算，弹性元件在空气中的模态频率与其固有频率差别极小，空气可近似为理想流体，并可认为弹性元件在空气中的附加质量系数近似等于1，即CM(air)≈1。则由式(7)可得弹性元件在空气中的附加质量系数的表达式：

(8)

将文中数值模拟的弹性元件外部流场为空气的对照组所得弹性元件的模态频率近似视为其固有模态频率，则处于任意介质中的弹性元件的附加质量系数可近似表达为：

(9)

通过对流体的阻尼效应给弹性元件施加的流体动力质量和附加质量系数的分析计算推导出的湿模态频率与附加质量系数的关系式，CM的数值可从文献[12]中查图获得，因此，式(9)为定量计算相关工况下的弹性元件模态频率提供了一种方式。

事实上，在湿模态下，弹性元件的振动模态频率的变化，会直接影响到弹性元件的传热情况，本文也对此进行了相关分析。

2 物理模型

弹性管束的材料为紫铜，配重块材料为不锈钢，具体材料属性如表1所示，结构参数如表2所示。

通过Solidworks建立弹性管束三维模型，并将模型导入Ansys Workbench，在Geometry模块生成直径600mm、高200 mm的管束外流体域，如图2所示，并划分有限元网格，进行网格独立性验证，选定弹性换热管及管束外部流体域网格数为823 073个。考虑实际工况的管外流体流速较低，选用标准模型，外部流场的工质分别选定为液态水和煤油进行计算，流体流动方向为自下向上，边界条件设置为速度入口、压力出口，壁面均为无滑移壁面。通过改变入口速度在Fluent模块中得到弹性元件壁面的压力和温度，由于是单向流固耦合，且最后计算的模态频率为稳态过程，所以无需设置时间步长；导入Pre-Stress Modal模块，预置外部流场的压力，在Modal模块的Acoustics插件中设置元件所处流体环境的声速与密度，该模块会根据设定的声速与密度计算得到弹性元件所处外部流场的黏度，最后根据Workbench中的程序框图进行流固耦合计算，得到弹性管束的湿模态频率，以此计算相应的附加质量系数。在Workbench中,湿模态运算过程如图3所示。

表1 弹性元件的材料属性

表2 弹性元件结构几何参数

图2 外部流体域模型

3 湿模态振动频率影响因素分析

根据理论分析，考虑黏度及来流速度的影响，本文

图3 Workbench湿模态运算过程

选取了水和煤油作为外流介质，并设置不同入口流速进行模拟计算，分析湿模态振动频率的影响因素，以及这些影响因素对弹性元件换热效果的影响。

设置外部介质为一个大气压下的液态水(室温)，并分别设置流体静止和入口流速为0.044 m/s和0.500 m/s时进行计算；相同工况下，工质选择煤油(室温)进行计算。两种介质的流场条件下弹性管束的前六阶湿模态频率及固有频率分别如图4和图5所示。

图4 弹性换热管在水中湿模态频率

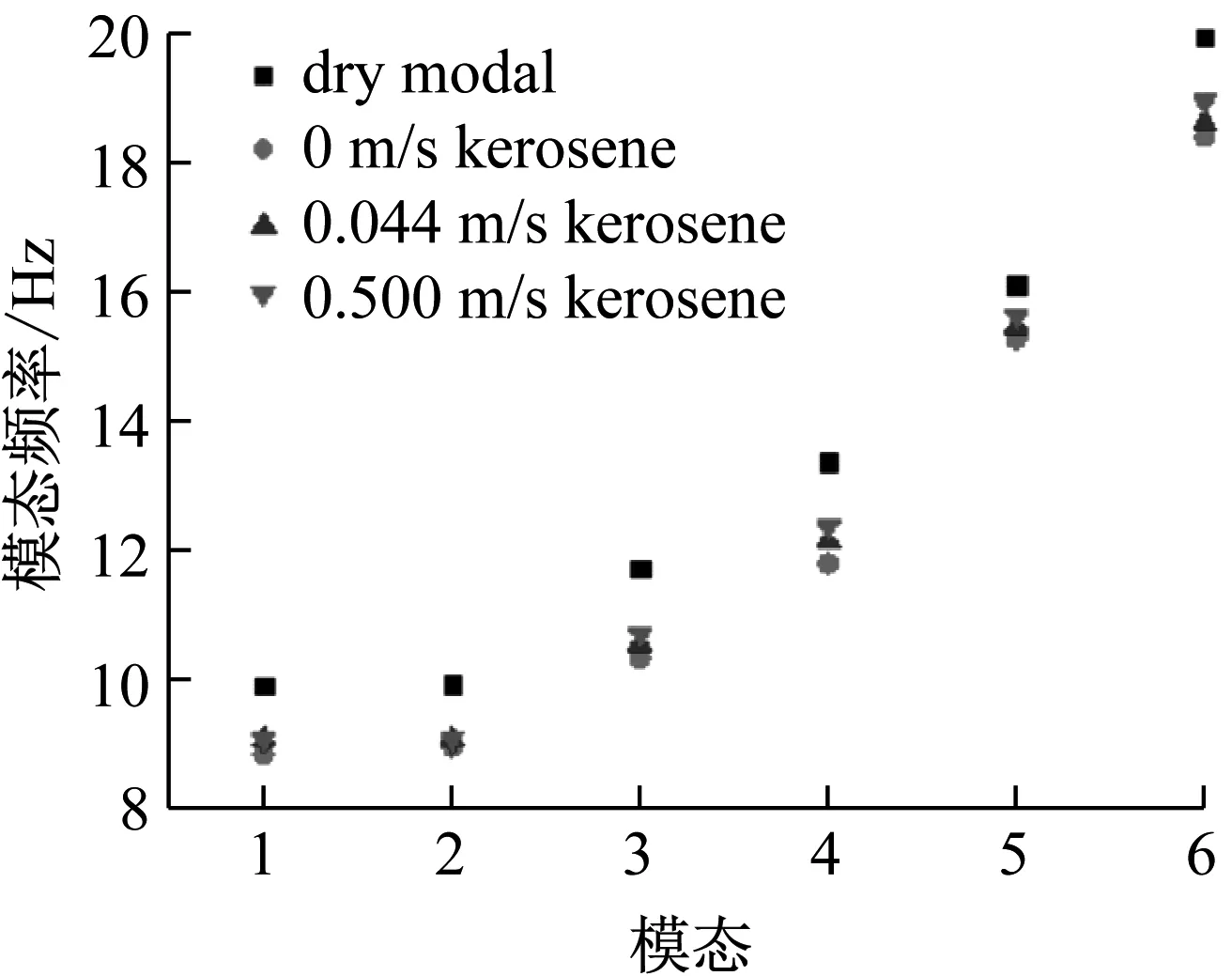
图5 弹性换热管在煤油中湿模态频率

外流场为液态水时，弹性管束各阶湿模态频率都较固有频率下降，流场速度为0时，弹性换热管束的湿模态频率较固有频率下降约1.3%～1.8%，外流场速度不为0时，各阶频率随流速的增加而上升。外流场为液态煤油时，弹性管束各阶湿模态频率下降显著，降幅约5%～11.3%，由于受到外部流场流速的影响，各阶频率随流速的增加有小幅上升。

根据图4和图5所示的模态频率，可用式(9)计算得到每一阶固有频率对应的附加质量系数，如图6所示。每阶模态的附加质量系数随着模态阶数升高而降低，黏度大的流体介质对应的附加质量系数明显大于黏度小的流体介质；在同种介质中，附加质量系数随流速增加而减小。

图6 各阶模态频率对应的附加质量系数

对处于不同流速的煤油中的弹性元件进行模态分析与附加质量系数计算，当外掠流体流速增加时，增加了弹性管束的张力，使其湿模态频率从处于静止状态下有所上升，一定程度上使附加质量系数下降。外掠介质为水时，改变工质流速对附加质量系数的影响并不大，实际计算数值差异极小；外掠介质为黏度大的煤油时，改变工质流速对附加质量系数有一定影响，计算结果如图7所示。

图7 煤油速度对附加质量系数的影响

4 湿模态振动对传热的影响

弹性管束换热器中，依靠管束振动强化传热。从上文的理论分析、数值模拟中可以看出，弹性管束换热器壳程的流体工况的改变会对弹性元件的模态频率产生影响，进而影响换热器内不同位置的弹性管束的传热效果。

文献[13]给出了振动与静止时管外表面换热系数的比较关系式如下:

(10)

式中：hv为振动时的弹性元件表面换热系数，h0为静止时的弹性元件表面换热系数，A为最大振幅，d为管外径，Rev为振动雷诺数[14]，Ra为瑞利数。文献[15]研究了悬臂圆管和椭圆管做振动管外流动与传热特性实验得出式(11)：

Nu=a·f·Rev·(A/d)0.4Pr0.8

(11)

式中:对于圆管，a=2.98。式(11)表达了弹性元件管外Nu数、振动雷诺数Rev、Pr数与振动频率f和比振幅(A/d)的关系。通过此式，可以计算圆管在一定频率下振动时对应的对流换热情况。

本文对弹性管束为换热元件的弹性管束换热器进行了相关实验，如图8所示。冷流体自下而上流过换热器的壳程，壳程流体温度沿壳程轴向逐步升高，其壳程流体的黏度会呈现沿壳程轴向自下而上不断降低的趋势。因此，每排弹性管束的模态振动特性受其影响而不同。为了探究这种影响，本文进行了层流状态下弹性管束换热特性的实验研究。

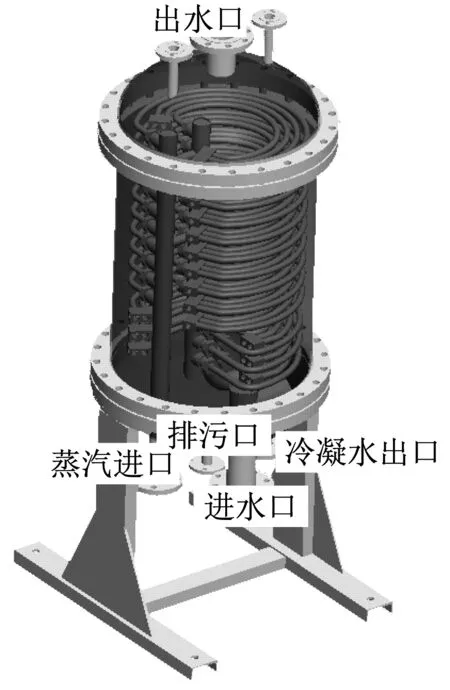
图8 弹性管束换热器轴测图

实验用的弹性元件及壳体直径与本文数值模拟尺寸相同，换热面由13排弹性管束与基管相连固定，实验系统图如图9所示。

图9 实验系统

为了对处于不同位置的弹性管束进行分析，获得每一排弹性管束周围外流场的局部工况，在相邻的弹性管束间及管壁布置了热电偶，相关的测点分布如图10所示。

根据实验数据获得不同位置的弹性管束的附加质量系数及其对应的管外Nu数，与上文通过数值模拟计算的相同工况下的附加质量系数CM及对应Nu数对比，得到Nu数随CM变化的趋势，如图11所示。

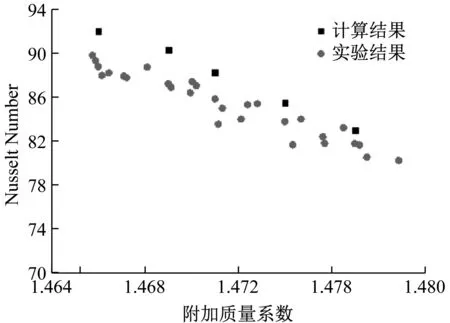
图11 Nu随附加质量系数变化情况

分析图11可得，实验值与理论计算的变化趋势一致，偏差在0.8%～4.5%，且大部分数据点的偏差不超过3%，在误差允许的范围之内，验证了数值模拟的可靠性。实验数据与理论计算数据存在偏差，分析认为，实验流场的波动会影响到弹性管束的随机阻尼，以及管束之间的相互影响，都会影响到弹性管束的实际振动情况，使其处于略低于相应工况下的计算得到的湿模态频率，进而影响了其换热情况。

根据上述实验与理论计算，我们可以得出结论，在整台换热器运行的过程中，外部流场的改变会使弹性元件的湿模态频率降低，使其附加质量系数增加，而弹性管束的换热效率则会随着附加质量系数CM的升高而下降；此外，我们可以通过附加质量系数CM来计算弹性元件的湿模态频率f，并由此估算附加质量系数CM对应的Nu数。

5 结 论

本文基于Ansys流固耦合的模态分析，对弹性换热管在不同外部流场下的湿模态振动频率进行了数值模拟。通过对附加质量系数的推导，得到了湿模态频率对应的附加质量系数关系式。分析了弹性管束的湿模态振动特性的影响因素及其对传热特性的影响。主要结论如下：

(1) 分析了弹性管束的湿模态频率与外流场黏度、速度的关系，推导了弹性管束湿模态频率与受到外流场影响而产生的附加质量系数的关系式。

(2) 弹性管束附加质量系数的存在使弹性管束的湿模态频率较其固有频率产生一定程度的下降。外掠流体的黏度对弹性管束的湿模态频率影响较大，黏度的增加会使湿模态频率下降，对应的附加质量系数增大；本文研究的流速范围内，外掠流体流速的增加会使附加质量系数有所减小，但其影响程度较小。

(3) 弹性管束受外部流场的影响，湿模态频率相对于固有频率有所降低，可以通过附加质量系数表达。附加质量系数越大，对应的值越小。