基于状态追踪特征相空间重构的轴承寿命预测方法

柏 林，闫 康，刘小峰

(重庆大学 机械传动国家重点实验室，重庆 400044)

作为旋转机械的重要组成部件，滚动轴承的状态监测及剩余寿命预测具有重要的学术研究意义与工程实践价值[1]。鉴于轴承故障物理模型的不确定性，基于数据确定的轴承寿命预测方法随着数据处理及智能信息技术的发展越来越受欢迎[2-4]。基于数据驱动的寿命预测方法核心在于状态变化敏感特征的优化选择、特征约简[5-7]及寿命预测模型优化的建立三个方面。针对提取敏感特征，申中杰等[8]以相对方根均值(Relative Root Mean Square，RRMS)作为轴承性能衰退评估指标，运用相关分析选取敏感特征，有效预测出轴承的剩余寿命，但当轴承运行工况发生改变是否RRMS还能准确对轴承状态进行评估无法考证。Ali等[9]利用均方根值熵估计法提取时域特征指标，并基于Weibull分布对该特征指标、均方根值及峭度进行拟合，将拟合后的结果作为最优特征，通过神经网络实现滚动轴承的剩余寿命预测，但仅仅三个特征不能全面表征轴承退化状态，在特征信息的完备性方面欠佳。在轴承剩余寿命预测中，为了更加准确地描述轴承退化状态，往往组建多域高维特征，但高维特征集之间存在较强的相关因子，其大量“冗余”信息不仅带来“维数灾难”问题，而且影响后续预测精度，有必要建立一个综合健康指数对轴承退化状态进行统一描述。何群等[10]采用PCA进行对高维特征集的降维融合，通过多变量极限学习机(Multivariate Extreme Learning Machine，MELM)进行了轴承寿命的预测。Zhao等[11]提出线性判别分析(LDA)进行轴承特征降维，最后利用多元线性回归(MLR)去估计轴承剩余寿命。这些降维及非线性映射方法，只是单纯从数学运算的角度进行有用信息再提取，存在着过度分解且映射特征无任何物理含义等缺陷。SVDD算法核心是将低维空间投射到高维空间，在数据样本超空间中建立一个正常数据足够多，异常数据排除在球外，利用该思想将滚动轴承全寿命特征数据正常时期建立超球体，而滚动轴承逐渐退化特征数据将越来越远离球心，这样可以将多维最优特征用一个综合健康指数统一描述，可较好刻画滚动轴承全寿命时期的退化状态。对于SVDD算法的核函数及惩罚因子的优化，引入ACPSO优化SVDD方法来建立滚动轴承退化的健康指数。近年来，人工神经网络以其强大的非线性拟合能力、并行计算能力、高容错性及多输入多输出等特点在轴承剩余寿命预测中取得了实质性的成效，但在其参数的优化选择及预测精度还有待继续完善。由于轴承在每个运行时刻并不是独立发生，而是上一步的运行状况往往影响着下一步的运行状况，为了合理准确描述轴承运行状态，将健康指数进行相空间重构，以重构指数为基础，将ACPSO优化后的GRNN作为轴承剩余寿命预测模型，计算结果相对于其他预测模型有更高的预测准确率。

1 特征提取

在准确预测轴承剩余寿命时，提取最优特征是分析轴承状态关键的一步，本文提取13个时域特征(s1-s13)以及13个频域特征(p1-p13)，共计26个特征，见表1，s1-s8为有量纲指标会随着故障的发展呈现上升的趋势，反映振动幅值和能量的关系；s9-s13为无量纲指标与设备的运行状况无关，反映振动信号的时间序列；p1反映了频域振动能量的大小；p2-p4，p6，p10-p13反映了频谱的分散或是集中程度；p5，p7-p9反映主频带位置的变化。在这所有特征中，部分特征可以较好的刻画轴承整个生命周期的状态，有些则不然，以往对于轴承特征优劣选择仅仅通过图像上进行单纯刻画，随着状态监测的发展，故障诊断与健康管理[12](PHM)及健康状态评估[13](HSE)应运而生，对于滚动轴承性能退化的演化趋势，应综合考虑演化趋势的单调性和敏感性，可定义一个量化指标，即轴承信号特征对于性能退化的跟踪能力TA，基于滚动轴承信号特征量化TA步骤如下：

(1) 提取轴承振动信号的特征；

(2) 对所有特征进行单调性评价，计算特征si描述性能退化趋势φi的单调性统计值为：

(1)

式中：φi(n1)和φi(n2)分别为特征曲线φi在n1和n2时刻对应的特征值，sign()为符号函数，N为特征si描述特征演化趋势曲线φi观测点总数，特征si描述特征演化趋势曲线的单调性和敏感性水平分别为：

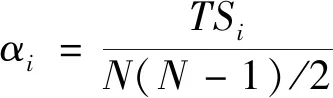
(2)

(3)

式中：median()为求中值函数，φi(1)为正常状态特征值，d(n1)和d(n2)分别为n1及n2时刻滚动轴承退化的严重程度，曲线d(nN)用轴承特征RMS进行替换；

(3) 综合考虑性能退化的单调性和灵敏性，量化各特征的性能退化跟踪能力为：

表1 时域和频域特征指标

TAi=[1+e-10(αi-0.5)]-1×[1+e-10(βi-0.5)]-1

(4)

2 特征约简

2.1 支持向量数据描述

SVDD[14]是由Tax等[15]提出的单分类方法，试图寻找一个包容目标样本的最优超球体，给定目标类数据集X={xi,i=1,2,…,m}，球中心设为o，半径为R，在算法中引入松弛因子ξi提高对野点的鲁棒性，最小化问题表示为：

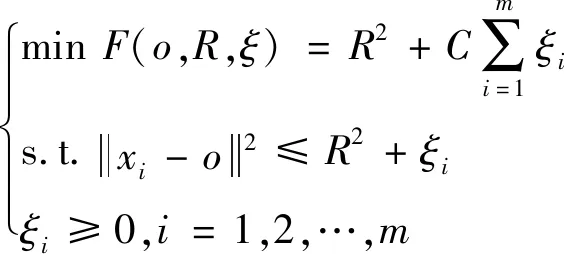
(5)

式中:C为惩罚参数，为求解上式优化问题，引入拉格朗日乘子与高斯核函数K(xi,xj)=(Φ(xi)·Φ(xj))，核函数能抑制原始特征数据的过分增大，更紧凑描述原始数据，可得超球体半径：

(6)

式中：xs为支持向量，βi，βj为拉格朗日乘子。新样本数据z到球心的广义距离为：

(7)

最后得到统一描述轴承全寿命状态的健康指数：

d=D-R

(8)

对于SVDD中惩罚参数C及核参数σ采用ACPSO算法优化选择。

2.2 自适应混沌粒子群算法

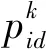
ω=(ωmax-ωmin)exp(-(τk/Kmax)2)+ωmin

(9)

式中：ωmax=0.9，ωmin=0.4，k为当前迭代次数，Kmax为最大迭代次数，经验值τ一般在[20,55]内取值，由于混沌Logistic模型形式简单，计算复杂度低，且当控制参数为4时趋向满映射，分布最均匀，已经满足PSO算法跳出局部最优解的需求，故本文选择混沌Logistic模型，混沌Logistic模型如下：

xn+1=4xn(1-xn)

(10)

式中：n=0,1,…，将xn+1替换粒子速度更新公式随机数rand，最终的ACPSO迭代公式：

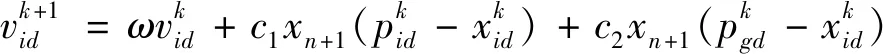
(11)

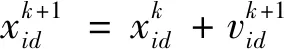
(12)

式中：d∈{1,2,…,D}，D为搜索空间的维数，c1和c2为学习因子，一般设置为2，用预测误差最小值作为评判最终健康指数，公式如下：

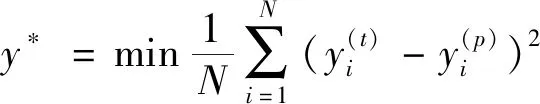
(13)

3 GRNN寿命预测模型

3.1 相空间重构

根据Takens提出的嵌入定理,一维时间序列经过相空间重构可准确表达原系统的动力学特征。对于时间序列{xi,i=1,2,…,n}，n为序列长度，重构相空间[18]为{xi,xi+τ,…,xi+(m-1)τ}，i=1,2,…,M，式中xi为相空间的点，m为嵌入维数，τ为延迟时间，M为重构相空间中相点的个数，M=n-(m-1)τ，其重构的相空间表示为：

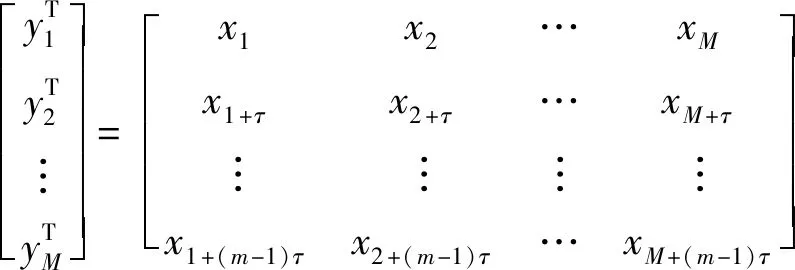
(14)

相空间重构的核心在于选择合适的嵌入维数m和延迟时间τ，本文采用最小互信息法选择延迟时间τ、CAO法[19]确定嵌入维数m，通过相空间重构形成的重构指数输入ACPSO-GRNN模型预测轴承寿命。

3.2 广义回归神经网络

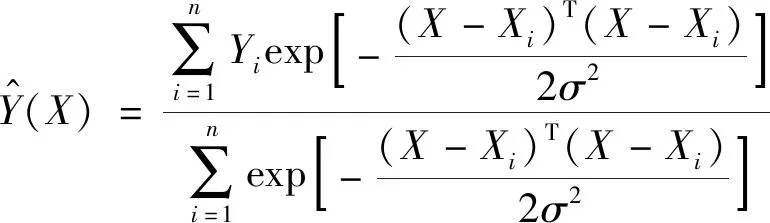
(15)

式中：Xi，Yi为样本观测值，σ为光滑因子，n为样本数目。对于σ的选取同样采用2.2的ACPSO算法进行优化选择，以平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)、相对均方根误差(RRMSE)四种误差之和作为预测寿命准确性的评判指标，相对于以一种误差作为评判寻优结果更加准确，公式见文献[10]。

4 本文方法步骤

具体步骤(见图1)：

(1) 从原始振动信号提取26个特征；

(2) 对所提特征归一化，采用五点平均滑移方法对特征进行平滑处理；

(3) 对特征进行单调性和敏感性评估，利用公式(1)～(4)量化26个特征对轴承退化状态跟踪能力的评定，设定阈值A为中间值0.5，筛选超过阈值的所有特征组成最优特征集P；

(4) 选取正常状态轴承最优特征集建立正常超球体，将全寿命特征集计算出广义距离，以公式(13)作为ACPSO优化SVDD的适应度函数，尽可能将正常状态特征集在超球体内以达到分类准确最大，利用公式(8)得到健康指数d；

(5) 将健康指数d分别与PCA、流形学习Isomap的第一主分量P1和I1进行对比；

(6) 从三者图像确定轴承正常、衰退及失效期，选取健康指数d的轴承衰退期进行剩余寿命预测；

图1 总体流程图

(7) 将衰退期健康指数d输入到ACPSO-GRNN模型预测，与传统GRNN模型进行对比；

(8) 将衰退期健康指数d进行相空间重构形成重构指数，将健康指数与重构指数分别采用ACPSO-GRNN模型预测进行对比；

(9) 以四种误差评价指标及算法所用时间与传统SVR和BP神经网络进行比较，最终得到经过相空间重构的重构指数的ACPSO-GRNN模型预测更为精确。

5 试验验证

为了验证本文提出方法的有效性，采用法国弗朗什-孔泰大学FEMTO研究所的PRONOSTIA实验平台[21]下的滚动轴承全寿命公开数据，实验平台见图2，传感器设置有温度传感器(PT100)和加速度传感器(DYTRN30358)，本文研究的是加速度传感器获取的振动信号，采样频率为25.6 kHz，数据采集卡(NIDAQCard-9174)每10 s采集一次数据，每次采集数据时长为0.1 s，每次采集2 560个数据点，选择载荷4 000 N，转速1 800 r/min工况1的轴承1-5与轴承1-6数据进行试验验证。

图2 PRONOSTIA试验台

提取轴承的26个特征，采用步骤3筛选出最优特征集P={s1,s3,s4,s5,s6,s8,p1,p2,p6,p10,p13}，图3表示所有特征的跟踪能力量化值。

图3 状态跟踪能力TA

将最优特征集P进行步骤4、5处理，图4、图5、图6分别是三种方法统一描述轴承性能退化图。

图4 PCA降维融合图

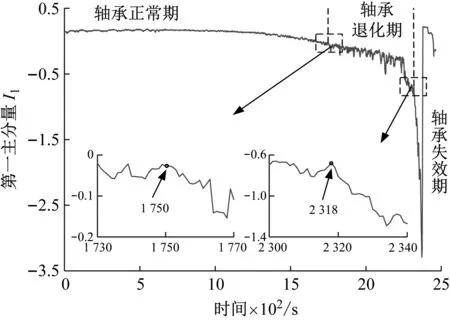
图5 Isomap降维融合图

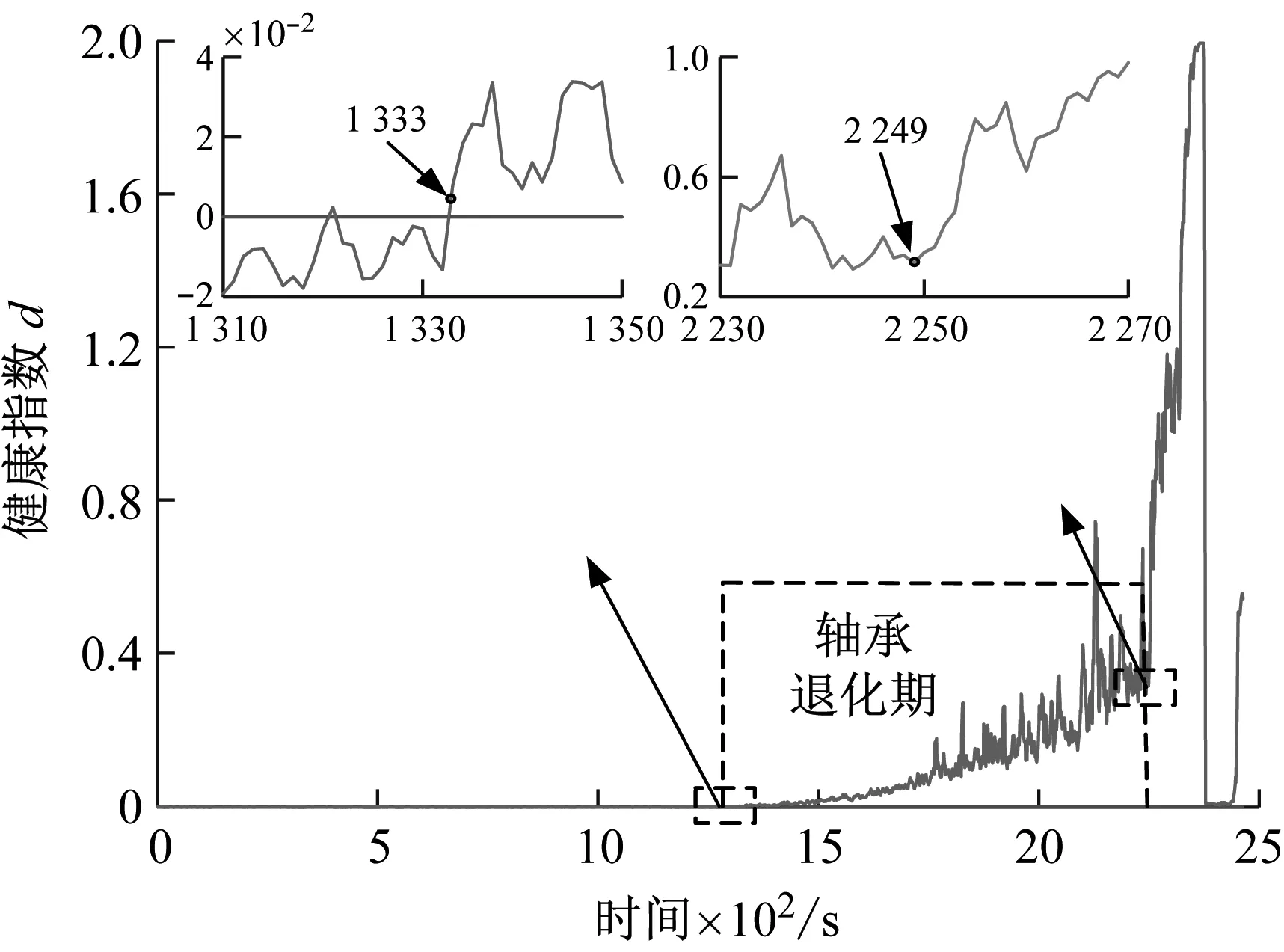
图6 SVDD健康指数图

从前两者特征降维融合图可以看出，均是1-1 749图像比较平缓，可见轴承处于正常期，从1 750-2 318，出现明显的主分量值跳跃增大，且幅值上下波动，轴承已然进入退化期，从2 318之后主分量值突然增大至骤然下降，说明轴承已失效损坏。

从健康指数图可以看出1-1 333健康指数处于0值之下，表明该时刻之前健康指数均在超球体内，轴承处于正常期，在1 333之后所有健康指数均大于0，轴承开始退化，健康指数开始上下波动，在2 249之后，健康指数突然增大至骤然下降，轴承进入失效期。从三者图像明显看出健康指数可以较早描绘出轴承开始进入退化期，且较早描述出轴承进入失效期，这样保证轴承在工程实际应用中较早发现问题，及时更换轴承。因此，选择本文所提的ACPSO-SVDD健康指数表征轴承性能退化趋势。

为了证明选择ACPSO-GRNN预测轴承寿命的有效性，采用与传统GRNN预测曲线进行对比，选用轴承1-5作为训练样本，轴承1-6作为测试样本，接着对健康指数利用3.1提出的相空间重构进行重构，经最小互信息法计算延迟时间τ为5，CAO法计算嵌入维数m为8，形成重构指数，再次进行轴承寿命预测，寿命预测点数为间隔10点预测，既可以加快算法运行速度同时也可得出精确的寿命预测曲线。如图7是健康指数通过GRNN模型优化前后的轴承剩余寿命预测结果，图8是健康指数与重构指数采用ACPSO-GRNN的预测剩余寿命结果。

图7 GRNN模型优化前后寿命预测结果

图8 健康指数与重构指数寿命预测结果

从图7、8可看出健康指数经相空间重构形成重构指数的ACPSO-GRNN预测模型相对于未重构健康指数的ACPSO-GRNN及未重构健康指数的GRNN预测准确精度更高，该模型基本预测走势与真实寿命相近，为了体现ACPSO-GRNN预测方法的优势，在同等条件下将ACPSO-GRNN与SVR和BP神经网络进行对比，其中健康指数、重构指数分别用HI和RI表示，如表2是步骤9四种误差评价指标及各头预测模型计算所用时间。

表2 预测模型结果对比

从表2可以看出RI-ACPSO-GRNN的四种预测误差均比其他预测模型低，尽管在算法的复杂度及计算效率比其他预测模型要高，但是所用的时间完全是在轴承寿命预测的可运行范围之内，故重构指数的ACPSO-GRNN预测模型既考虑了轴承准确的运行状况且所预测的误差更小。

6 结 论

(1) 提出一种量化特征对轴承性能退化描述的方法，通过量化特征跟踪能力，可有效筛选具有代表性的最优特征。

(2) 采用SVDD算法有效地将轴承运行状态进行了划分，相对于之前人工划分更具有说服力，可提高后续预测寿命的精确性。

(3) 提出将相空间重构引入到寿命预测中，更加符合轴承运行状态，对预测结果更具真实性，经过试验数据的验证，证明了相空间重构的预测轴承寿命方法精确度更高，具有一定的实用性。

(4) 算法所用时间在轴承寿命预测的可运行范围之内，利用ACPSO-GRNN预测算法相对于传统SVR和BP神经网络更具预测准确性。