考虑滑动轴承时变动力学参数的齿轮系统建模及分析
魏 维,郭文勇,吴新跃,吴启豪
(海军工程大学 动力工程学院,武汉 430033)
齿轮-轴承传动系统广泛应用于汽车、航空、航天以及船舶等领域,其运行状态对所在系统有重要的影响。在高速重载的工况下,齿轮-滑动轴承系统相较于齿轮-滚动轴承系统具有较高的稳定性,且由于滑动轴承具有较大的刚度和阻尼,有利于减小振动和噪声等级[1],因此随着对系统性能要求的不断提高,齿轮-滑动轴承系统的动态特性研究也受到越来越多的重视。
在理论研究方面,目前已建立了众多的齿轮模型。这些模型从单自由度到多自由度,考虑了内、外部激励以及多种非线性因素,例如时变啮合力、偏心、制造误差、齿侧间隙等。Kahraman等[2-4]研究了单对直齿轮的非线性特性,同时建立了多自由度系统动力学模型,并考虑了齿侧间隙对模型的作用,探究了不同参数对系统的非线性振动影响。Velex等[5-6]探究了啮合齿轮中摩擦力的作用,解析了摩擦和瞬态冲击与齿轮参数的相关联系,提出用摄动法描述包含时变齿轮啮合、弯曲-扭转-横向振动的三维齿轮啮合动力学模型。王庆等[7]利用集中参数法建立了斜齿轮传动系统的模型,考虑了传动误差、齿侧间隙和时变啮合刚度的影响,分析了系统的动力响应特性。随着齿轮系统动力学研究的深入,考虑滑动轴承特性对系统的影响显得越来越有必要。Baguet等[8]考虑了轴承间隙,建立了齿轮-轴-轴承系统的模型,分析了耦合系统的动态响应和振动特性。张将等[9]建立了考虑轴承间隙的齿轮系统模型,综合分析了轴承间隙对系统动力学特性的影响。Liu等[10]研究了直齿轮系统中齿侧间隙与轴承间隙相互作用的非线性特性,分析结果表明轴承间隙使得系统具有了自适应特性。总体而言,对齿轮系统的研究已较为全面,综合考虑了多种因素对系统的影响。
Sternlicht[11]提出将轴承的刚度和阻尼作为轴承的动力学参数。在以往的研究中通常将滑动轴承的动力学参数视为定值,但在实际的齿轮-滑动轴承系统中轴承支撑力、轴承阻尼和刚度是时变的,都会随着轴心位置、轴承间隙以及齿轮转速的变化而变化[12-13],且这种变化会对系统产生怎样的影响以往的文献也少涉及。
为了分析时变轴承动力学参数对齿轮系统的影响,本文建立了齿轮-滑动轴承耦合动力学模型,提出了考虑滑动轴承动力学参数的齿轮动态特性计算方法,综合考虑时变啮合刚度、时变齿侧间隙等因素,分析了轴承间隙、齿侧间隙、齿轮转速对系统动力学的影响规律,为实际中分析齿轮-轴承系统提供重要的理论依据。
1 分析模型
1.1 齿轮-滑动轴承耦合模型
图1为考虑滑动轴承动态特性的齿轮-轴承系统耦合动力学模型。假设:齿轮轴为短刚性轴,不考虑其弯曲和扭转;齿轮轴两端的轴承具有相同的参数和动力学特性;轴承为刚性支撑。本模型中不考虑齿面摩擦以及偏心对系统的影响。
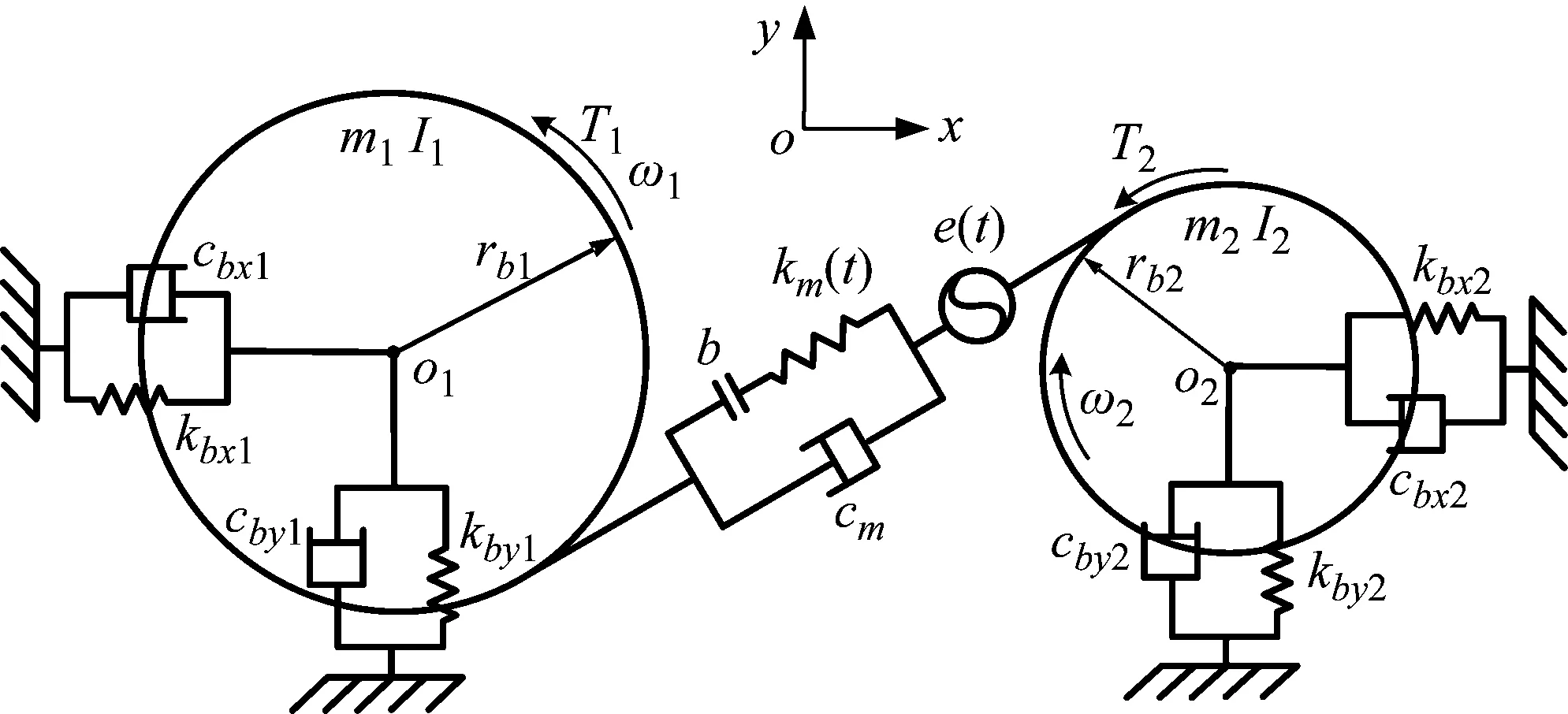
图1 齿轮系统动力学模型
设图1中齿轮的齿数分别为z1和z2,基圆半径为rb1和rb2,Ob1和Ob2分别为主动轮和被动轮轴承的轴心,O1和O2是两齿轮轴的形心和质心,齿轮中心与轴承中心的偏心距分别为eb1和eb2。由假设条件可以得出系统具有6个自由度,设广义位移为{x1,y1,θ1,x2,y2,θ2},其中x1、x2为两齿轮的横向位移,y1、y2为两齿轮的纵向位移,θ1和θ2为齿轮1、2的扭转位移。kbx1、kby1、kbx2、kby2分别是主动轮和被动轮轴承的支撑刚度,cbx1、cby1、cbx2、cby2是轴承的支撑阻尼,Fbx1、Fby1、Fbx2、Fby2是轴承的支撑力,上述参数为轴承的动态特性参数,与齿轮啮合运动有关,需要对轴承动态特性进行求解。
1.2 滑动轴承油膜力及动态参数计算
图2中动压滑动轴承示意图,图中Ob为轴承中心,Oj(x,y)为轴颈中心。R为轴瓦半径,r为轴颈半径,e为偏心距,h为计算点A的油膜厚度。根据几何关系推导,可得油膜厚度h的表达式为
h=C+xcosθ+ysinθ
(1)
式中:C=R-r为轴承间隙。

图2 动压滑动轴承示意图
采用文献[14]中轴承润滑模型,不可压缩(ρ不变)、层流状态下(不考虑湍流影响)、黏度不随压力变化的非定常Reynolds方程为
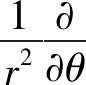
(2)
式中:θ为圆周角坐标,z为轴向坐标,ω0为轴的转速,η为润滑油黏度。同时有
(3)
采用有限差分法对雷诺方程进行求解可得轴承油膜压力分布。通过对所得油膜压力积分可求得油膜合力,轴承的油膜合力即为轴承对齿轮系统的支撑力,是轴承承载能力的体现。对油膜压力沿x和y方向积分可得油膜分力Fx、Fy:
(4)
(5)
当轴心在平衡位置作微小振动时,可将轴承的油膜简化为弹簧和阻尼的组合,根据文献[15]采用压力扰动法,得到平衡位置处轴承刚度和阻尼的计算公式为
(6)
(7)
(8)
(9)
(10)
将式(10)中所得的扰动压力值代入式(6)~(9)中,经积分可得到轴承的刚度和阻尼值。通过以上计算过程可知,轴承的刚度以及阻尼与轴承的轴心位置有关,当轴承位置随时间变化时轴承的刚度与阻尼也随之发生变化。
1.3 动态齿侧间隙及动态啮合力
随着齿轮的转动以及轴承间隙的变化,齿轮的中心坐标随着时间发生变化进而引起啮合中心距以及啮合角的变化,进而使得齿侧间隙也处于动态变化中,动态齿侧间隙可表示为
b(t)=2b0+2a0cosα0(invα′(t)-invα0)
(11)
式(11)中b0为初始齿侧间隙,α=tanα-α,α′(t)=arccos(a0cosα0/a′(t)),a0、α0为初始安装中心距和压力角,a′、α′为齿轮运行过程中的中心距和压力角。其中动态中心距可表示为
(12)
根据齿侧间隙的分段特性,动态间隙的非线性函数可用以下公式表示
f(x,t)=

(13)
齿轮系统受到激励力的作用,在平衡位置做微小振动,将振动状态的x方向的相对位移以及y方向的相对位移转换到啮合线上,如图3所示。
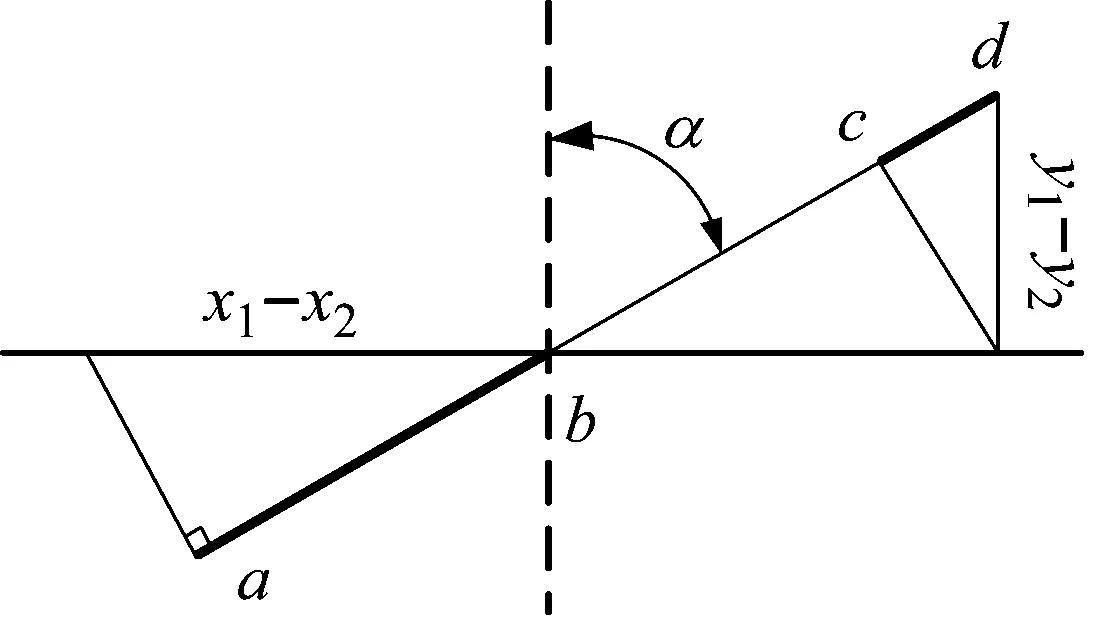
图3 齿轮啮合线相对位移
图3中x方向到啮合线的转换关系为(x1-x2)sinα,用线段ab表示,y方向到啮合线的转换关系为(y1-y2)cosα,用线段cd表示。综合考虑齿轮扭转方向转换到啮合线上的线位移,以及齿轮的静态传动误差e(t),由动态激励引起的齿轮动态传动误差可表示为:
δ(t)=rb1θ1-rb2θ2+(x1-x2)sinα+
(y1-y2)cosα-e(t)
(14)
通常静态传动误差随齿轮转动而呈现周期变化规律,可认为其是含有周期项的平稳随机信号,为了便于分析,用傅里叶级数对e(t)进行标示:
(15)
式中:em为传动误差均值,ei为谐波项的幅值,ωh为啮合频率,φe=φi+π为ei对应的相位角。考虑到计算的简便性,通常只考虑静态传递误差的一次谐波。
直齿轮的啮合刚度随着啮合位置和啮合轮齿对数的变化而变化,呈现周期性变化的特点,本文利用傅里叶级数表示齿轮的时变啮合刚度,其基频为啮合频率
(16)
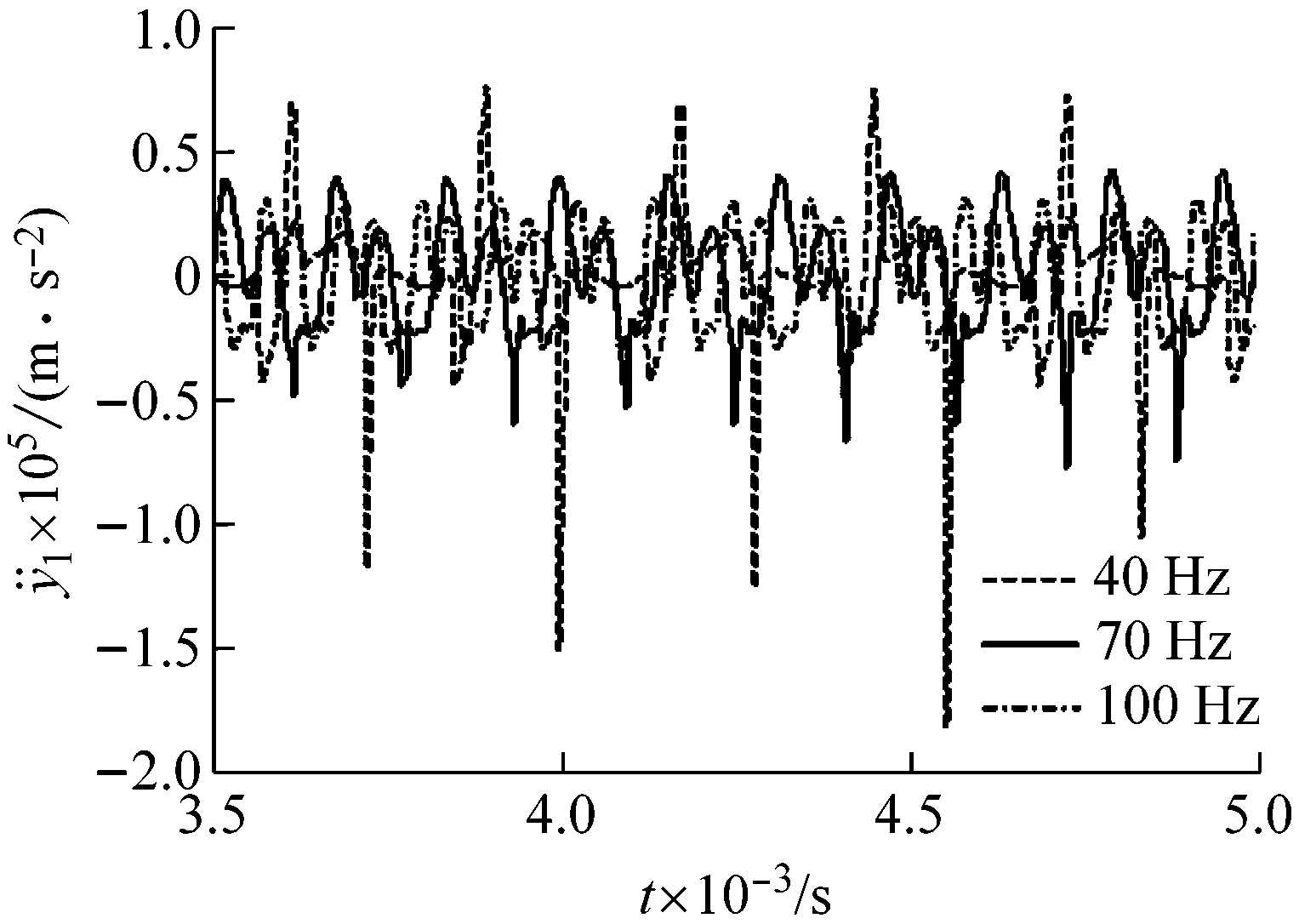
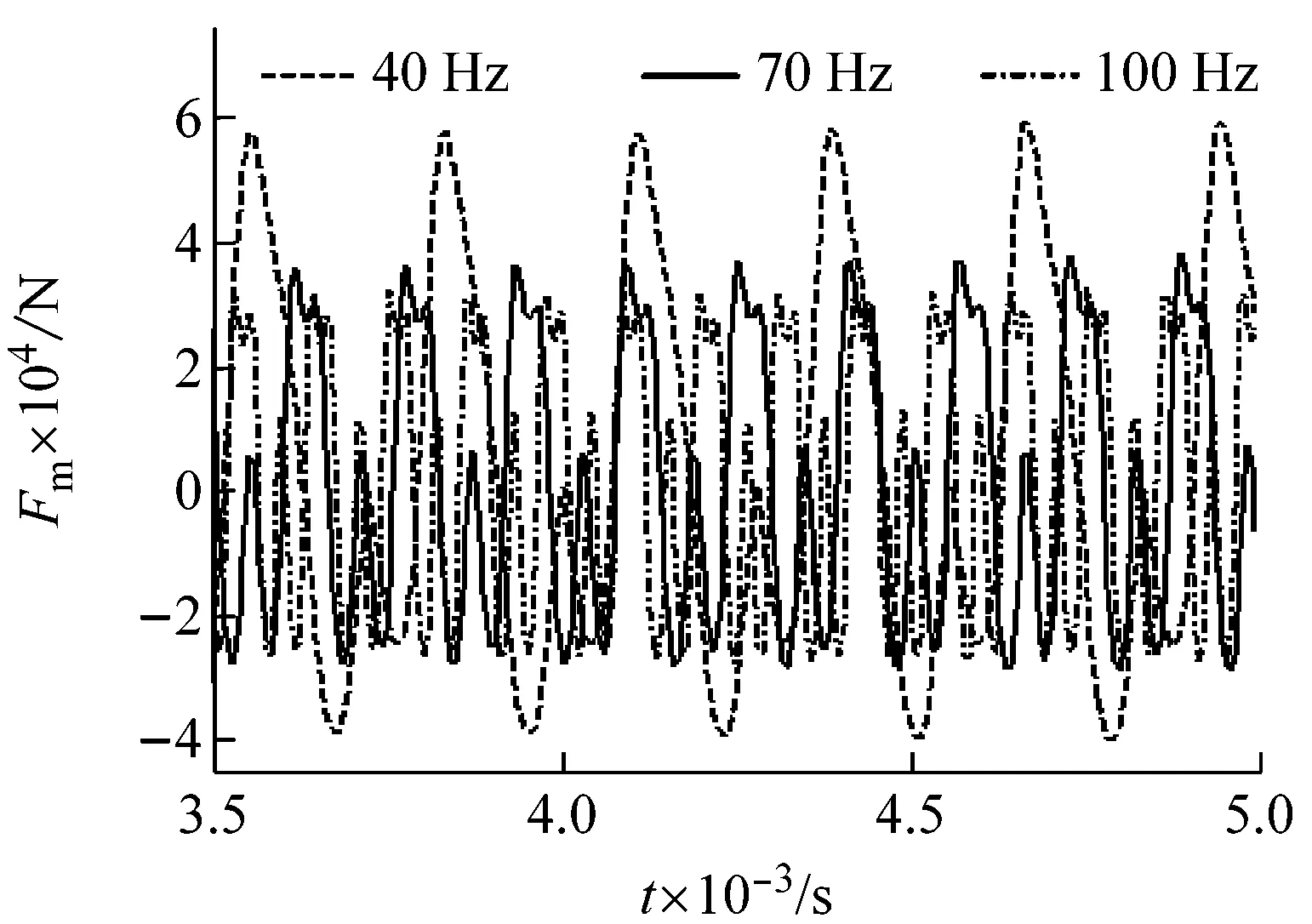
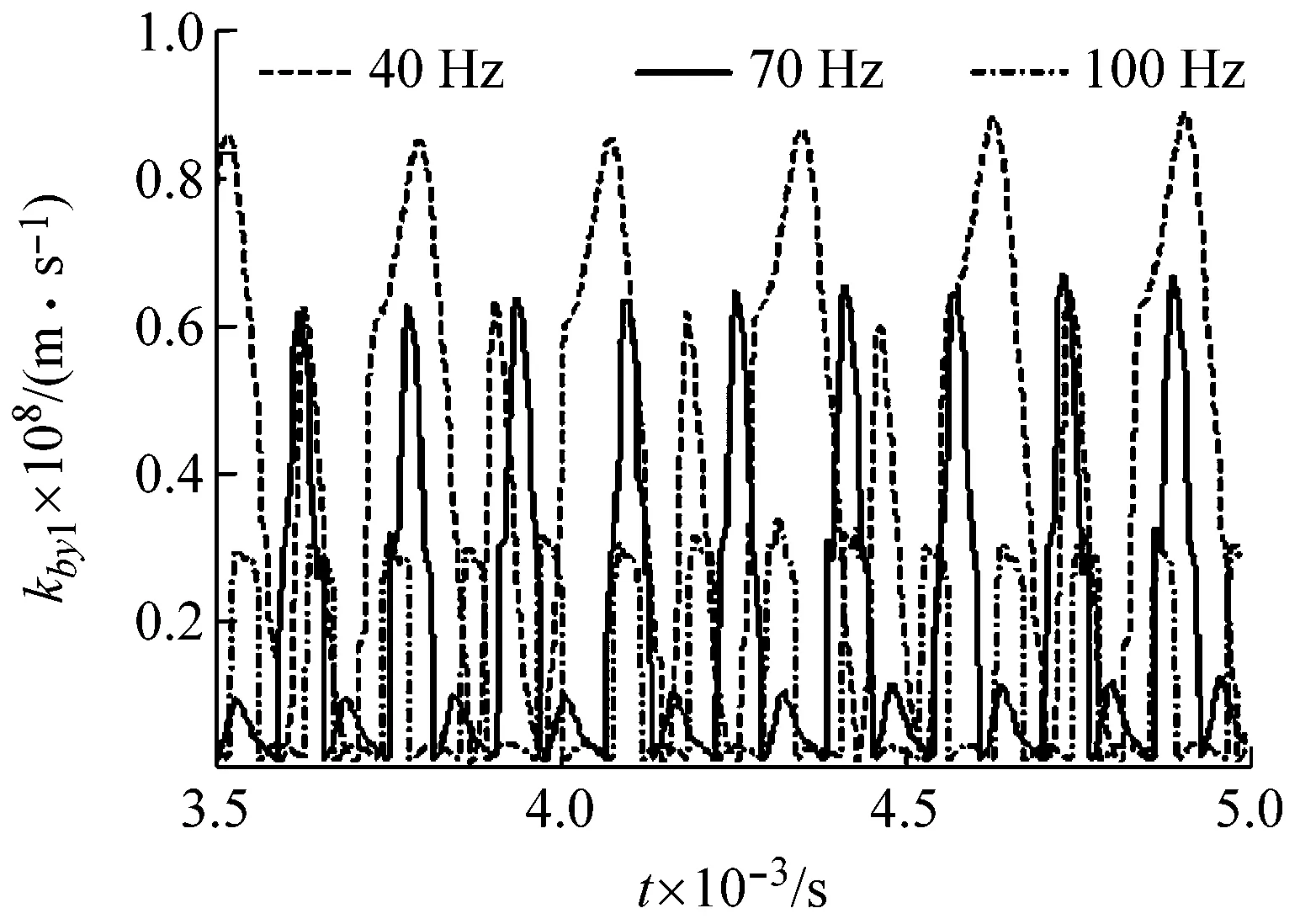
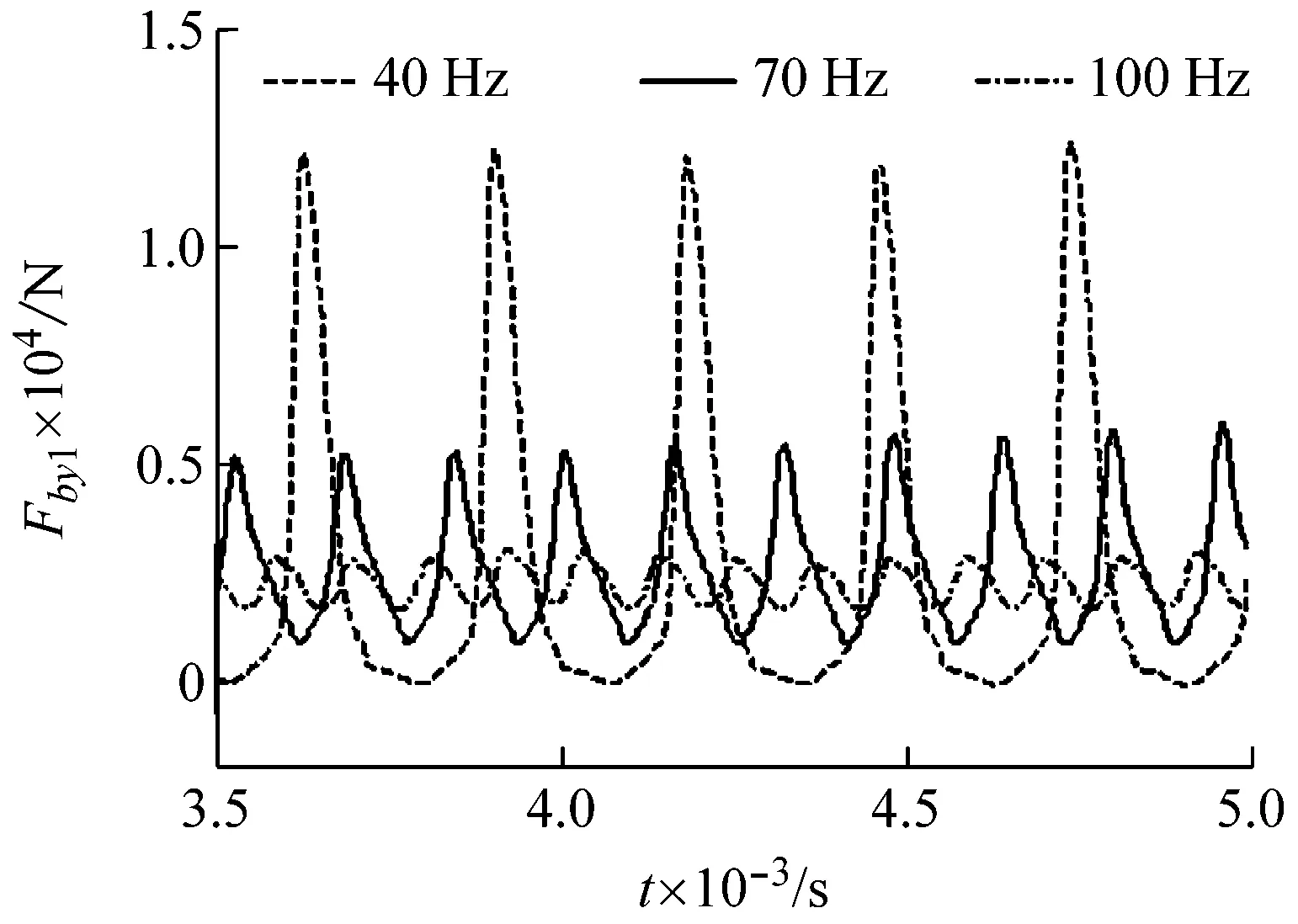
式中:k0=εks,ε为齿轮啮合重合度,且有m<ε (17) 式中:ζ为啮合相对阻尼比。综合上述分析可以得到齿轮啮合线上的动态啮合力为 (18) 根据图1的模型,对齿轮系统应用拉格朗日方程,得到考虑动态齿侧间隙的单级圆柱直齿轮系统运动微分方程: (19) (20) 式中:I1、I2为齿轮的转动惯量,T1为输入力矩,T2为负载力矩。 滑动轴承与齿轮间存在着相互耦合的作用。一方面,齿轮的动态响应是轴承的外部激励,齿轮轴心的动态变化影响着轴承油膜力、刚度和阻尼的大小;另一方面,轴承油膜力、刚度以及阻尼又影响着齿轮系统动态啮合力的变化。由于考虑了轴承与齿轮之间的耦合作用,传统的计算方法已无法满足求解的需要,为此本文提出了一种适应于求解齿轮-滑动轴承耦合系统求解的计算方法。 耦合系统求解流程如图4所示。首先设定系统的初始参数,假设在初始齿轮轴心坐标(x1(0),y1(0))和(x2(0),y2(0))处轴承处于静平衡状态,考虑载荷平衡条件对轴承的雷诺方程进行求解,进而根据式(4)~(10)求得轴承的刚度(kbx1(0)、kby1(0)、kbx2(0)、kby2(0))、阻尼(cbx1(0)、cby1(0)、cbx2(0)、cby2(0))以及油膜力(Fbx1(0)、Fby1(0)、Fbx2(0)、Fby2(0))。然后根据初始坐标求解齿侧间隙b(0)以及初始动态啮合力Fm(0),将以上计算结果代入齿轮运动微分方程中进行求解,得到下一时刻的齿轮轴心坐标(x1(1),y1(1))和(x2(1),y2(1))。重复上述步骤直到数值仿真计算时间ts结束。 图4 齿轮-轴承耦合系统求解流程图 齿轮-滑动轴承系统在船舶动力传动中有着重要的应用,其性能的好坏直接决定了船舶动力系统的工作性能,因此文本在齿轮-滑动轴承数学模型的基础上对其进行数值仿真,以研究轴承间隙、齿侧间隙、转速对系统振动特性的影响。本文采用5阶定步长Runge-Kutta算法对系统微分方程进行求解。 为了确保建模与计算方法的通用性,取文献[10]中的齿轮、轴承参数如表1,表2所示。 表1 齿轮结构参数 表2 滑动轴承结构参数 研究轴承间隙大小对系统振动响应的影响规律。取初始齿侧间隙b0=10 μm,主动轮转频为60 Hz(3 600 r/min),分别计算当承间隙为Cr=39 μm、49 μm和59 μm时系统的振动响应特性,数值仿真结果如图5所示。 主动轮y向振动加速度曲线如图5(a)所示,由图中可以看出,随着齿侧间隙的增加,齿轮振动加速幅值明显减小,且当轴承间隙为59 μm时振动加速度变化更加平稳,无冲击出现,说明增加齿轮轴承的间隙能够起到降低振动加速度的作用,增加系统运行的平稳性。 (a) 主动轮y向振动加速度 (b) 时变啮合力 (c) 轴承y向时变刚度 (d) 轴承y向油膜力 图5(b)中显示了不同轴承间隙下啮合力的变化情况,由图可以看出在滑动轴承支撑的情况下齿轮啮合平稳,并且随着轴承间隙的变化啮合力的变化不大,同时啮合力随时间正负交替变化,说明齿轮啮合时出现了双边接触。图5(c)和图5(d)显示了轴承刚度以及油膜力的变化情况,由图中曲线可知轴承的刚度和油膜力在系统运行时不是固定不变的,而是随着齿轮的转动呈现周期变化的规律,且轴承刚度和轴承油膜力均随着轴承间隙的增加而减小。 (a) 主动轮y向振动加速度 (b) 时变啮合力 (c) 轴承y向时变刚度 (d) 轴承y向油膜力 研究齿轮转速对系统振动响应的影响规律。取初始齿侧间隙b0=10 μm,轴承间隙为Cr=39 μm,分别计算当转动频率为40 Hz(2 400 r/min)、70 Hz(4 200 r/min)和100 Hz(6 000 r/min)时系统的振动响应特性,数值仿真结果如图7所示。 本文建立了齿轮-滑动轴承耦合动力学模型,提出了考虑滑动轴承动力学参数的齿轮动态特性计算方法,综合考虑时变啮合刚度、时变齿侧间隙等因素,分析了轴承间隙、齿侧间隙、齿轮转速对系统振动响应的影响规律。通过对数值仿真结果的分析可以得到以下结论:滑动轴承的动力学参数具有时变特性,且这种变化有助于改善齿轮系统的振动特性,使得齿轮啮合得更加平稳;在一定范围内增加轴承间隙以及齿侧间隙能够减小齿轮的径向振动和啮合力幅值;随着转频的增加,系统的振动响应幅值减小,运行状态趋于稳定。 (a) 主动轮y向振动加速度 (b) 时变啮合力 (c) 轴承y向时变刚度 (d) 轴承y向油膜力1.4 系统微分方程
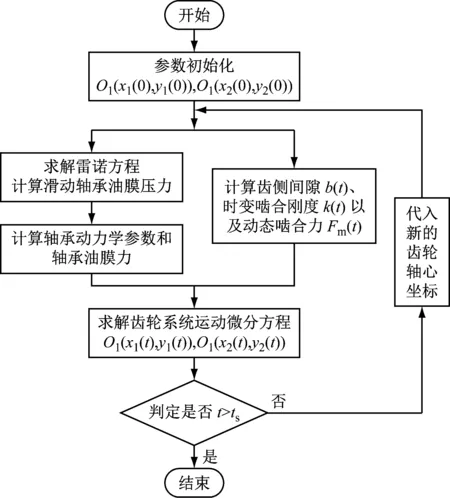
2 齿轮-轴承系统耦合求解方法
3 数值仿真


3.1 轴承间隙对系统振动特性的影响


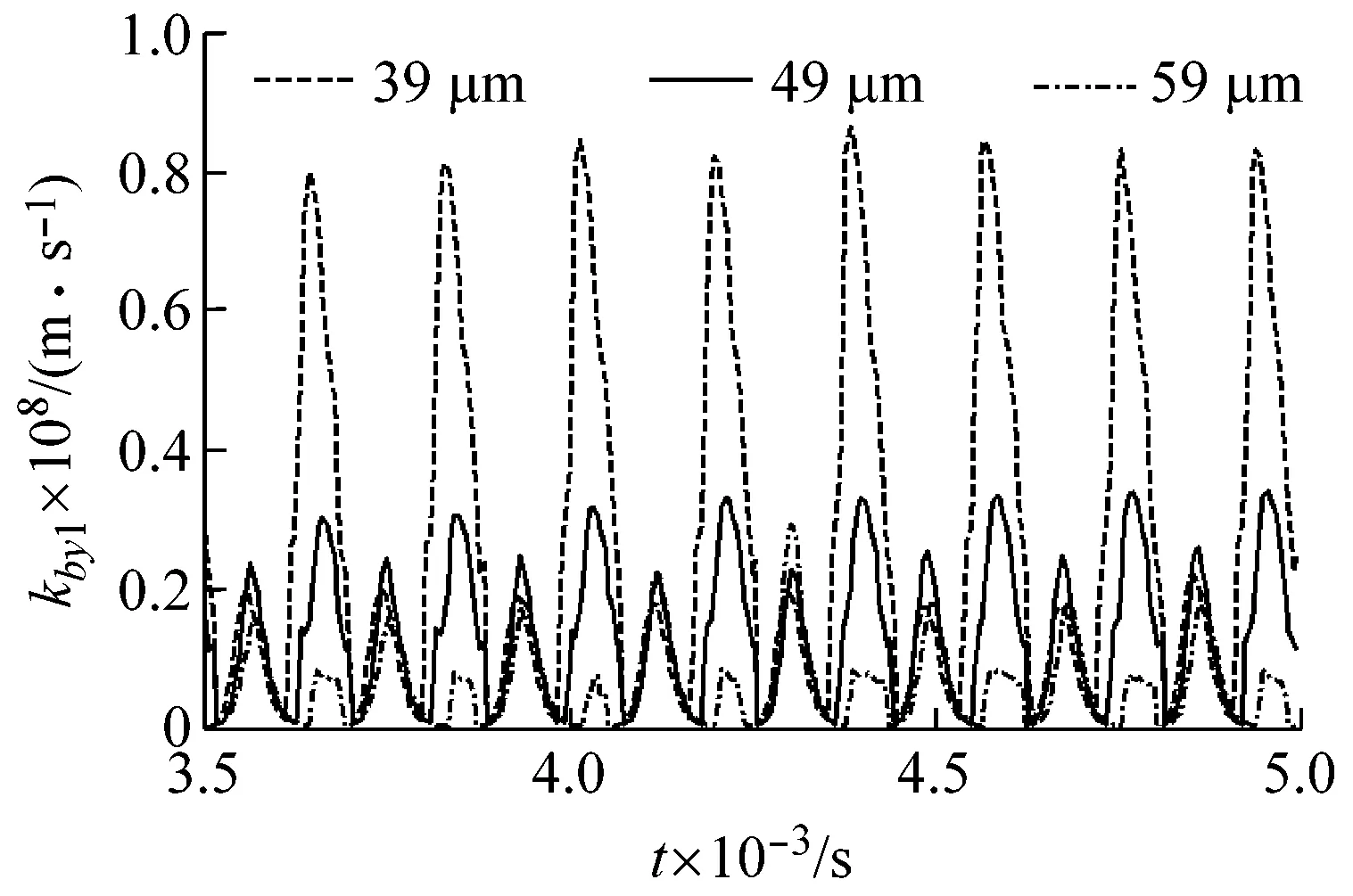
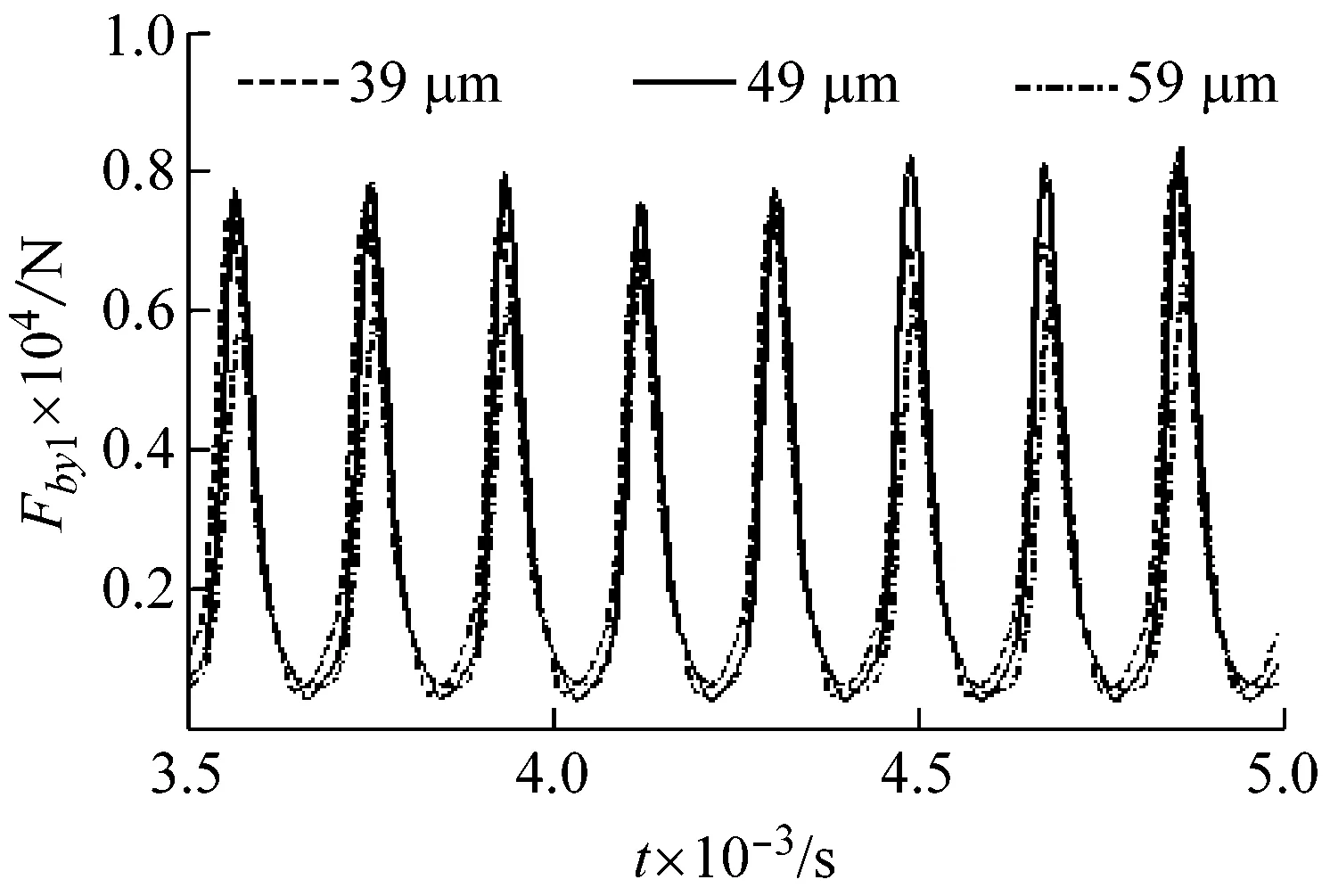
3.2 齿侧间隙对系统振动特性的影响
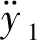
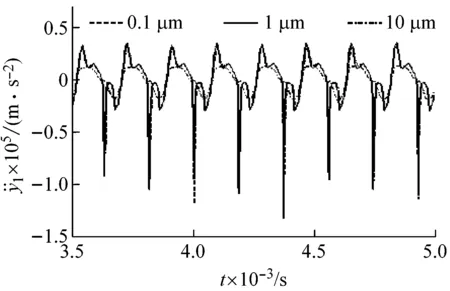
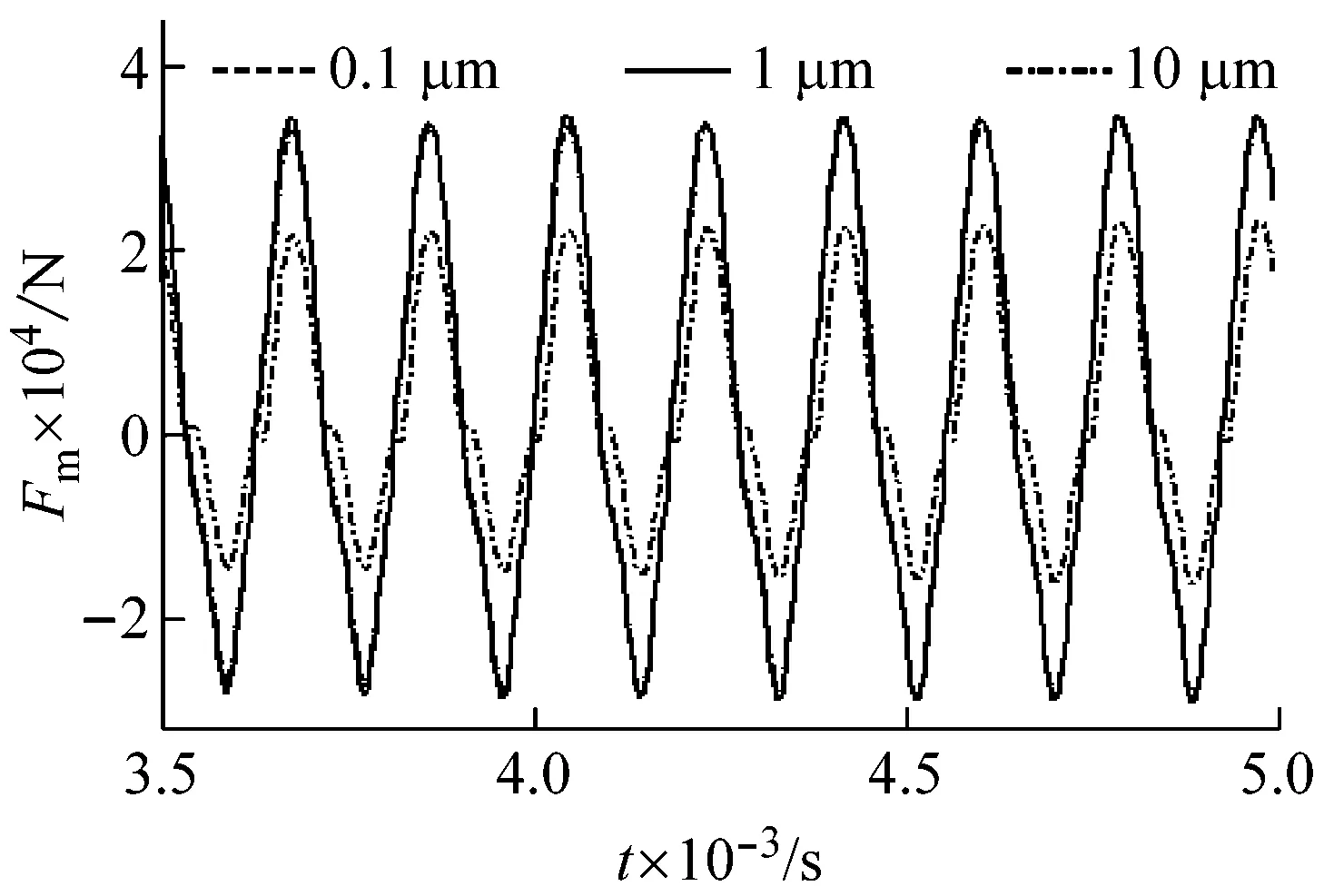
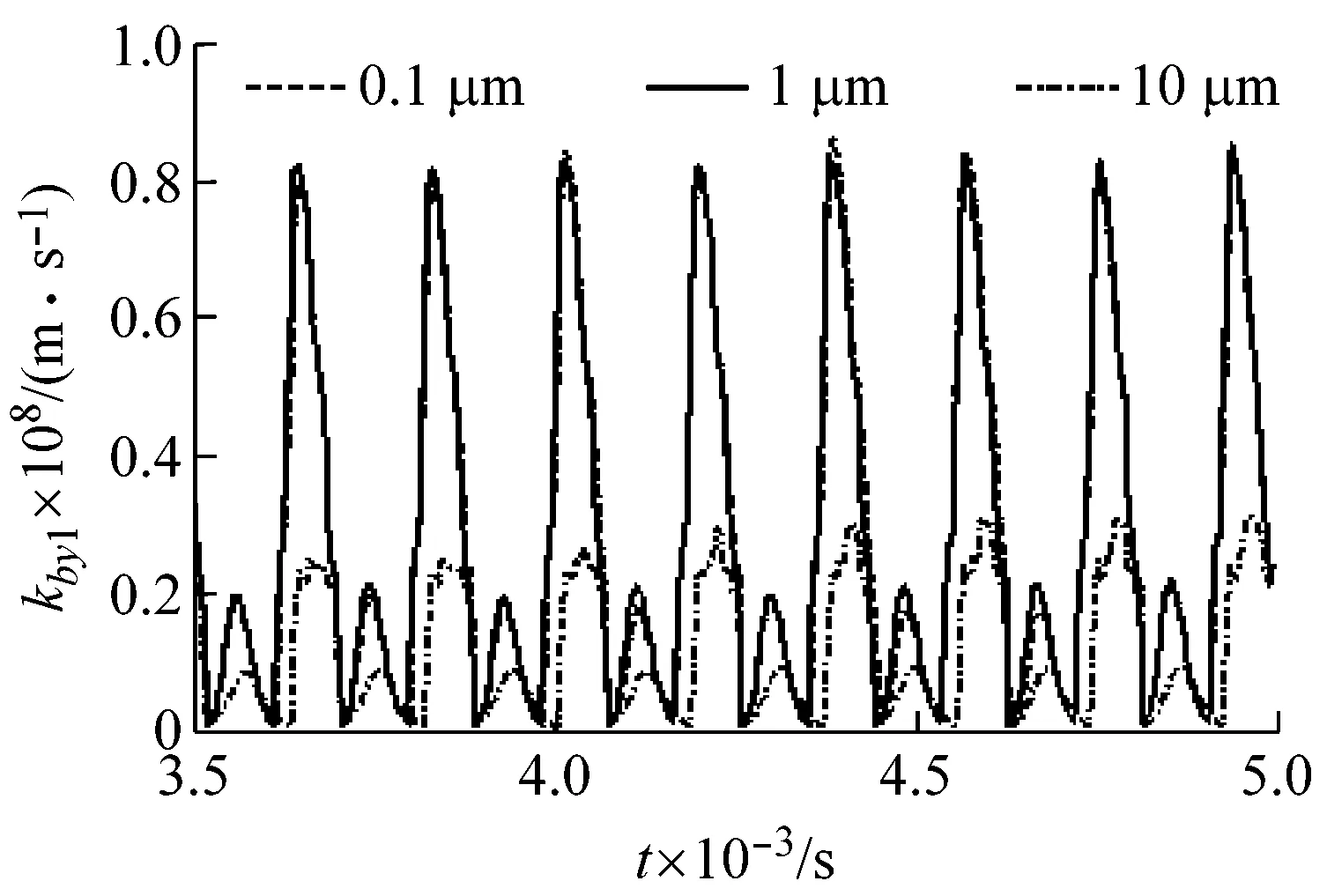
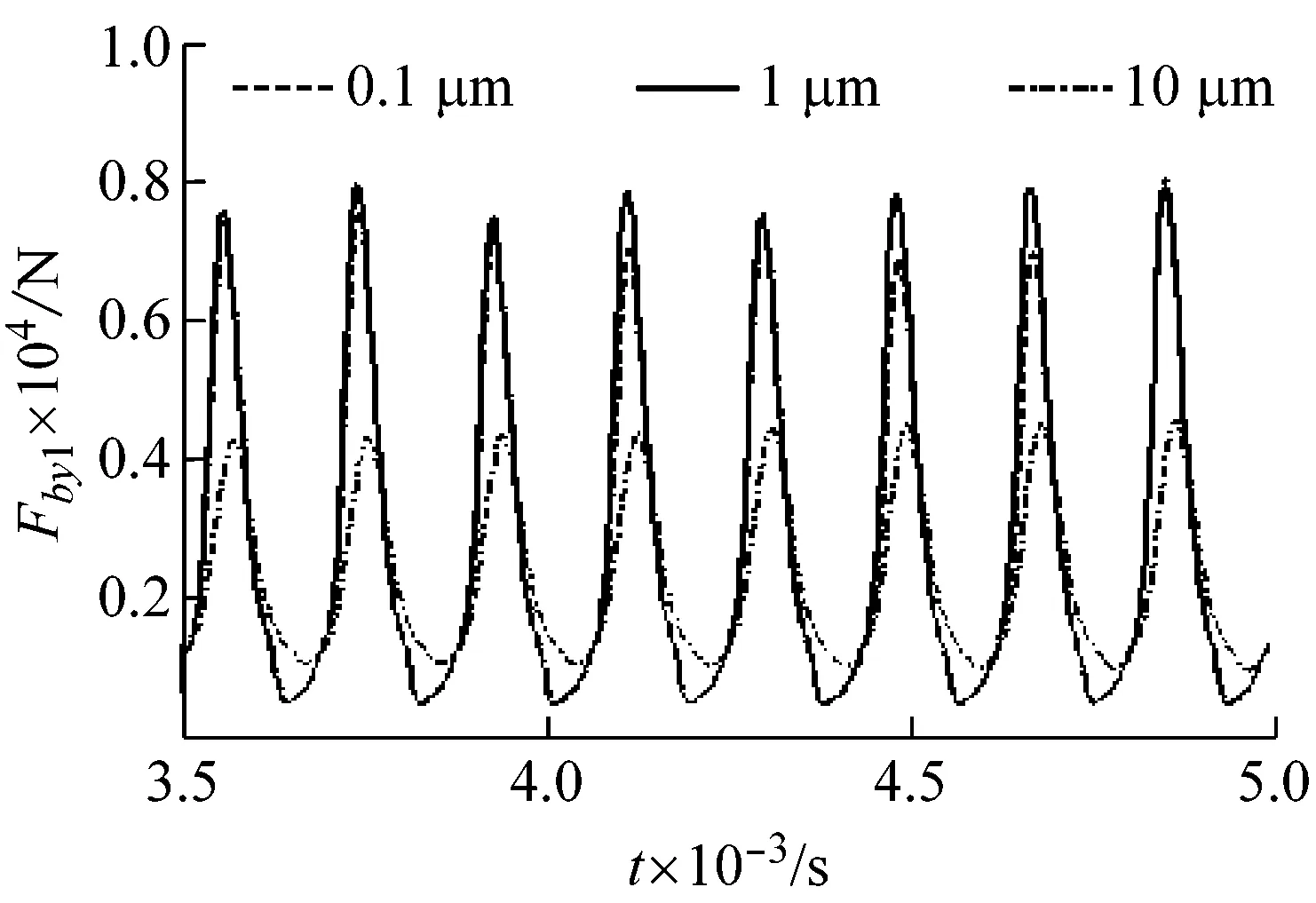
3.3 转频对系统振动特性的影响
4 总 结