尾流激励下的叶片气动力快速分析

罗 骁，李立州，张新燕，张 珺，杨明磊，原梅妮

(1.中北大学 机电工程学院，太原 030051； 2.太原学院 数学系，太原 030001)

航空发动机中存在气流导向的静叶和对外做功的动叶，如图1。当上下游叶片相对转动时，上游叶片流场的尾流会使下游叶片表面气动力产生周期性振荡[1-3]，引起叶片强迫振动[4-6]，甚至导致叶片疲劳破坏[7]。因此研究上游尾流作用下叶片的气动弹性振动对发动机设计有着重要的意义。

数值模拟方法是研究非定常流下叶片气动弹性的主要方法，但其计算效率较低，工程应用不便[8-10]。气动力降阶模型(Reduced Order Model, ROM)是描述叶片气动力特征的简化数学模型[11-14]。近年来，气动力降阶模型发展迅速，并被广泛用于叶片和机翼颤振[14-18]的研究。其中，常用谐波平衡法来描述时域和空间中的非线性周期性流场，并对其求解[15]。Ekici等[6]用谐波平衡方法研究了叶片颤振，认为该方法的结果与势流理论的结果符合较好。Ashcroft等[18]用谐波平衡法研究了二维压气机叶栅在亚音速和跨音速条件下的颤振特性，发现谐波平衡法可以准确地预测叶栅的颤振。He[15]通过一阶谐波法对叶栅周围流场非定常流分离的情况进行了研究，准确的预测了叶栅的颤振。现有气动力降阶模型的研究集中在机翼和叶片的颤振方面，没有涉及上游尾流激励下叶片的振动。针对这一问题，本文基于谐波平衡法提出尾流激励的叶片气动力降阶模型方法。对该气动力降阶模型方法的进一步研究发现：小扰动情况下尾流谐波引起的叶片气动力谐波和尾流谐波的振幅比例系数只与尾流频率有关。基于这一发现，本文进一步提出基于谐波平衡法和影响系数法[19-20]的尾流激励下的叶片气动力快速分析方法。该方法首先得到叶片气动力谐波振幅和尾流谐波振幅的比例系数；再拟合出这些比例系数与尾流谐波频率的关系曲线；通过该曲线和气动力降阶模型快速计算叶片气动力且不需要反复的CFD分析。

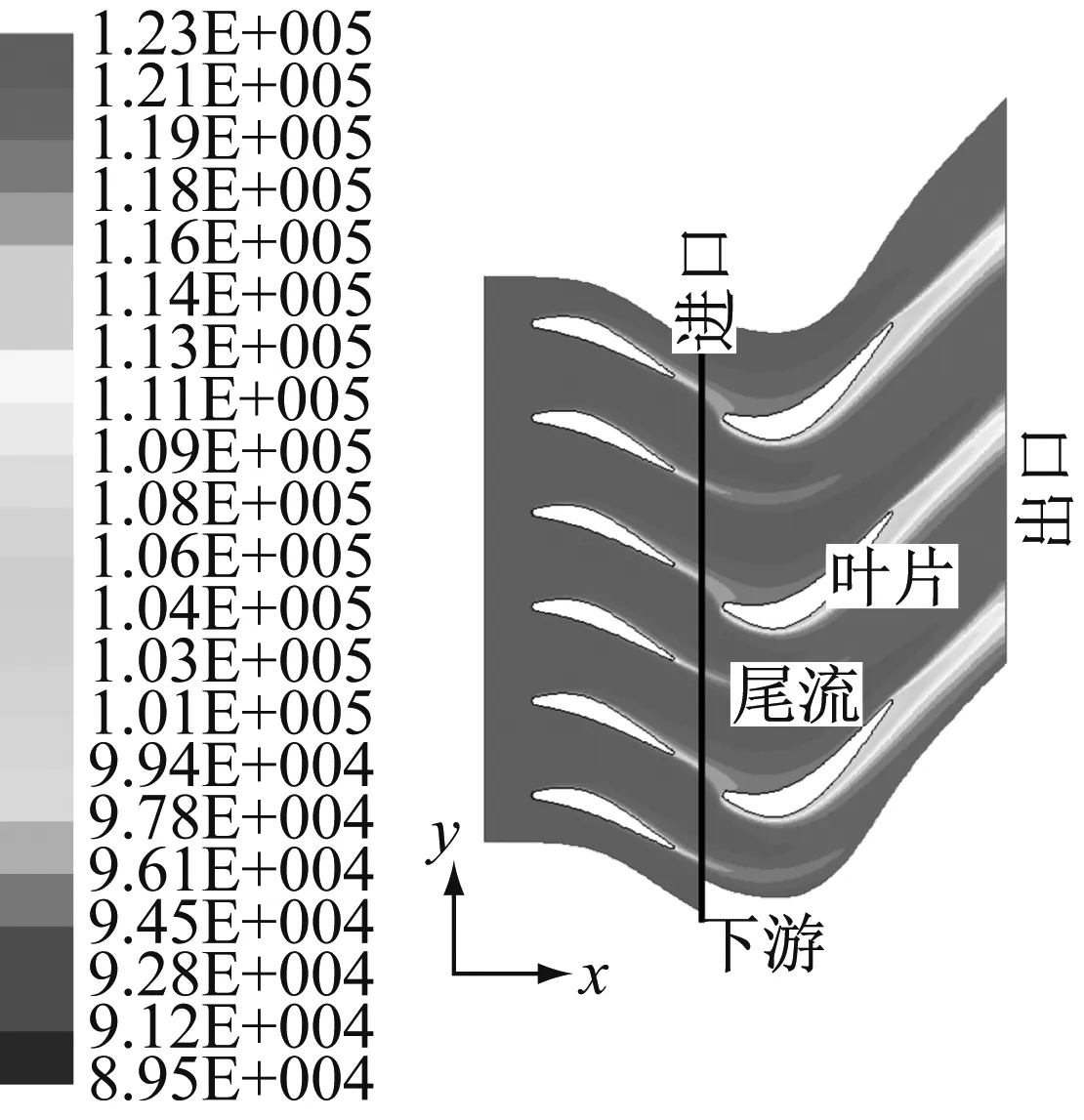
图1 尾流作用下叶片流场

1 尾流激励下的叶片气动力快速分析方法

本文以二维叶片(见图2)为例，介绍尾流激励的叶片气动力快速分析方法。设二维流场受上游尾流波动的持续激励(见图2)；上游尾流以恒定速度w在流场进口处移动，下游叶片流场随上游尾流的移动而振荡，使得整个叶片气动力周期性振荡。描述二维叶片周围流场的动量方程为：

(1)

式中:u为x方向流速，v为y方向流速，p为压力。

在进口x=x0处移动的尾流边界条件可以用傅里叶级数表示为：

(2)

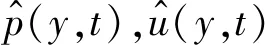
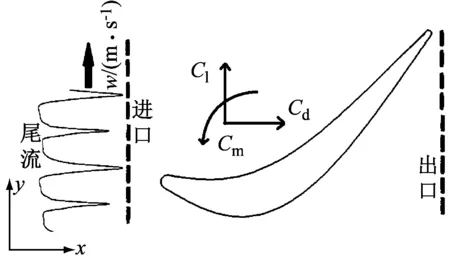
图2 尾流激励的叶片气动力系统

1.1 基于谐波平衡法的气动力降阶模型方法

根据谐波平衡法线性化理论[1,10,15]，在小扰动情况下周期性尾流激励的流场可以用傅里叶级数表示为：

(3)

将公式(3)代入公式(1)，按照文献[1]整理可得谐波分量的振幅方程如下：

(4)

将公式(3)代入公式(2)，则在进口边界上有：

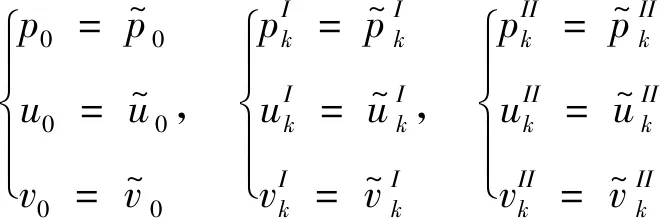
(5)

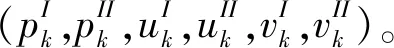
(6)

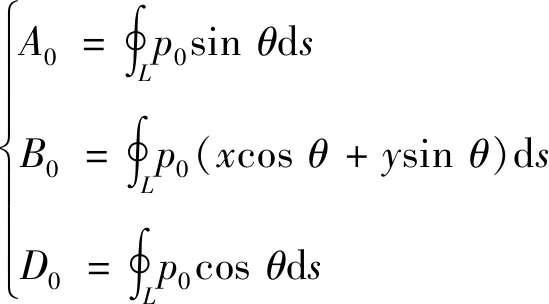
在小扰动条件下，采用以上方法需要建立公式(4)和公式(5)进行繁琐的求解。为简化这一过程，本文基于以上方法的理论，借助CFD求解各频率下叶片气动力谐波振幅和尾流谐波振幅之间的关系建立气动力降阶模型。公式(6)中叶片气动力与上游尾流同频。由此，建立尾流激励下的叶片气动力降阶模型如下(见图3)：

① 通过傅里叶变换将尾流分解为不同频率的尾流谐波。

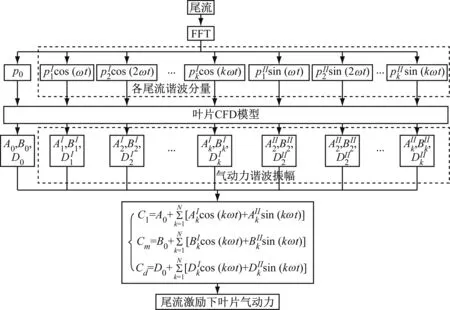
图3 气动力降阶模型方法

② 计算尾流傅里叶分解后定常状态下的叶片气动力。

③ 将各尾流谐波加载在CFD模型进口，获得各尾流谐波引起的叶片气动力谐波，并得到这些气动力谐波的振幅。

④ 将③中的气动力谐波的振幅代入公式(6)得到尾流引起的叶片气动力。

1.2 基于影响系数法的叶片气动力快速分析方法

上述尾流激励的叶片气动力降阶模型只能计算给定频率尾流下的叶片气动力；一旦尾流的频率发生改变，则需重新进行各频率谐波下叶片气动力的CFD计算。为此，本文对基于尾流激励的叶片气动力降阶模型方法深入研究，发现尾流激励下的叶片气动力振幅与尾流振幅之间存在相互影响[19-20],进一步提出了尾流激励的叶片气动力快速分析方法。

(7)

(8)

基于这一想法，本文建立尾流激励的叶片气动力快速分析方法的步骤如下(见图(4)：

1) 计算定常状态下叶片气动力稳态值A0，B0，D0。

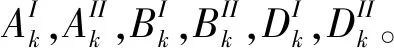
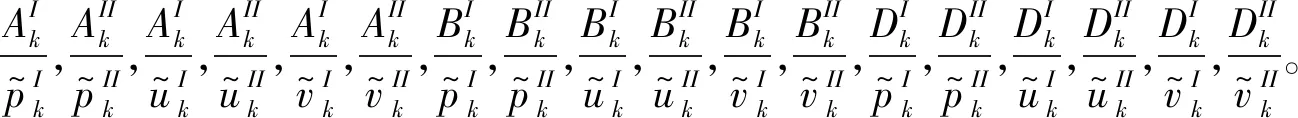
4) 拟合出3)中振幅比例系数与谐波频率的关系曲线。

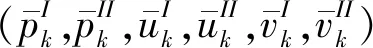
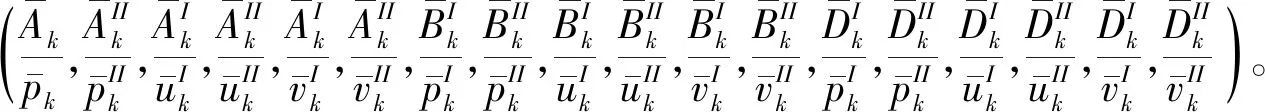
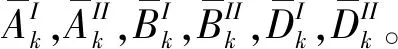
8) 将7)中的气动力谐波振幅代入公式(6)，可获得已知尾流激励的叶片气动力响应。

2 方法验证

以上游尾流在进口的压力波动为例验证本文方法。流场CFD模型见图5。叶片流场采用fluent求解，理想气体，Spallart-Allmaras模型，无滑移壁面，稳态进口总压120 300 Pa，稳态出口压力为101 325 Pa，温度为300 K。尾流以10 m/s的速度沿着进口y方向移动。

2.1 气动力降阶模型验证

流场进口边界压力随时间的变化见图6实线。对该压力进行傅里叶分解，取前7阶波形，求得的傅里叶级数的系数见表1。用7阶傅里叶级数拟合的尾流压力波形见图6虚线。

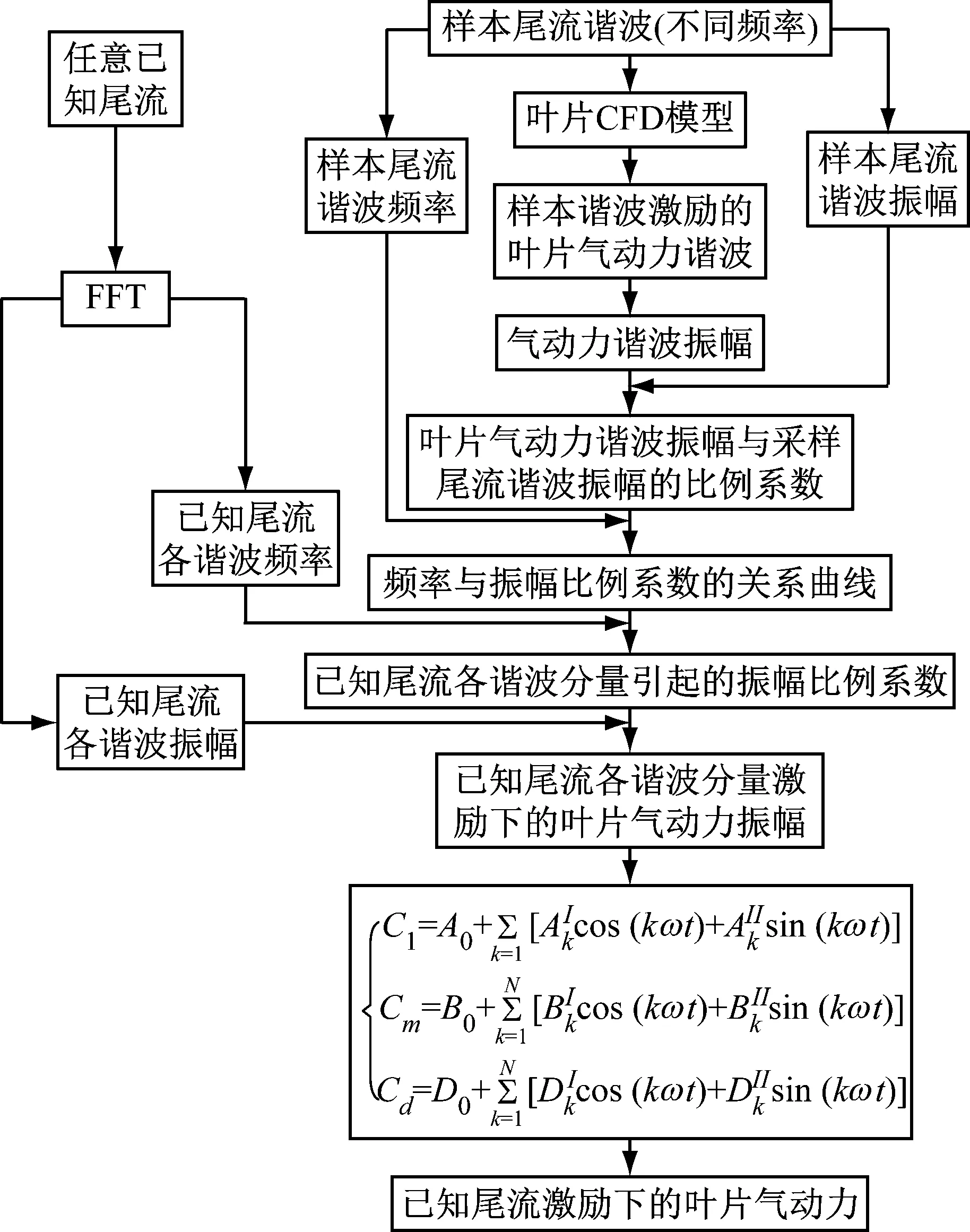
图4 尾流激励下的气动力快速分析方法

图5 流场CFD模型

按照前述气动力降阶模型方法，将表1中各频率下的尾流谐波逐个加载到CFD模型进口，计算得到叶片气动力各谐波振幅。计算结果见表2，将表2的气动力振幅代入公式(6)，就可以得到尾流引起的叶片气动力响应(见图7虚线)。图7(a)为尾流激励的叶片升力，图7(b)为叶片力矩，图7(c)为叶片阻力。

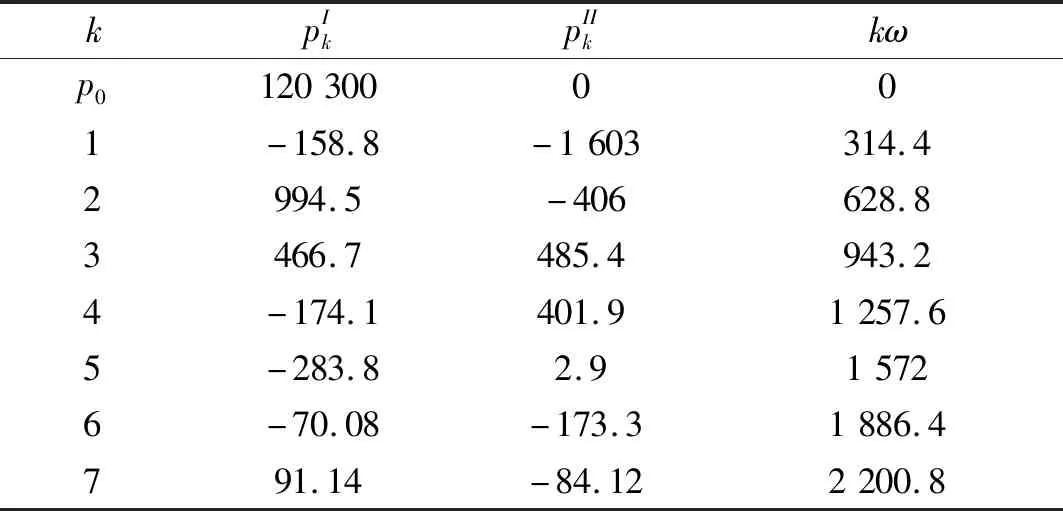
表1 尾流傅里叶级数展开的系数和频率

图6 尾流波形及其傅立叶级数拟合

表2 叶片气动力振幅

(a) 升力

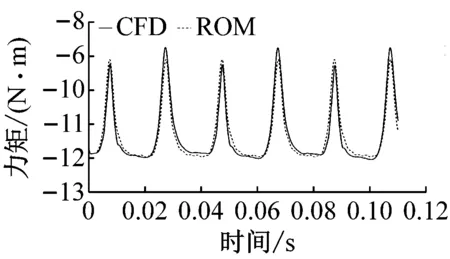
(b) 力矩

(c) 阻力

为验证降阶模型的结果，用CFD模型计算了图6尾流激励下的叶片气动力(见图7实线)。从图7可以看出：降阶模型的结果与CFD的结果一致。由此可知，尾流激励的叶片气动力降阶模型方法是可行的。

2.2 尾流激励的叶片气动力快速分析方法的验证

将3.1节中得到的各叶片气动力谐波振幅与尾流谐波分量的振幅相除，获得各频率kω对应的振幅比例系数,见表3。

拟合这些振幅比例系数与频率kω的关系曲线(见图8)。图8(a)、图8(b)和图8(c)分别为升力、力矩和阻力振幅比例系数与频率kω的关系曲线(见图中实线)。图8中“*”为样本采样点的叶片气动力振幅比例系数。

表3 叶片气动力谐波振幅与尾流谐波振幅的比例系数

Tab.3 The ratio between the amplitude of aerodynamic force of blade and the frequencies of wake harmonic

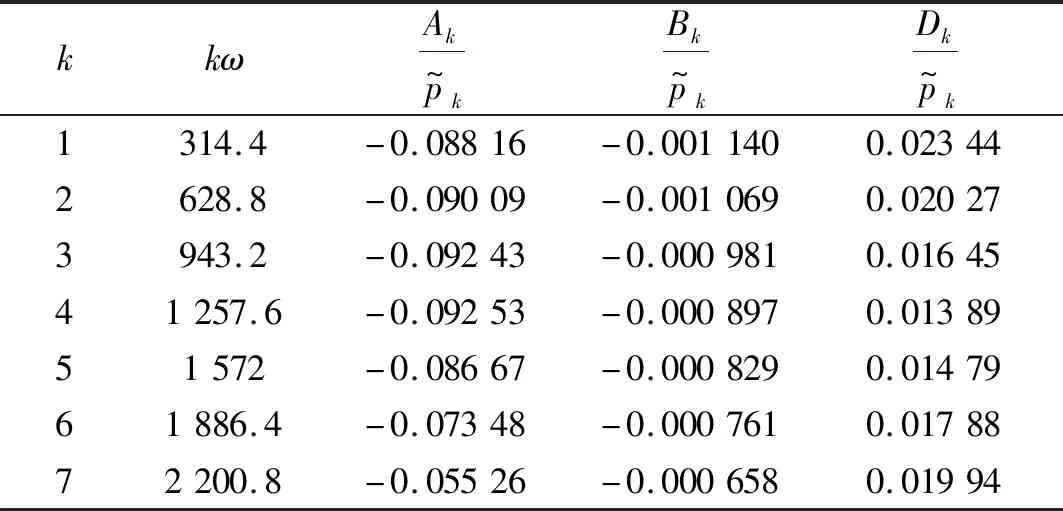
kkωAkp～kBkp～kDkp～k1314.4-0.08816-0.0011400.023442628.8-0.09009-0.0010690.020273943.2-0.09243-0.0009810.0164541257.6-0.09253-0.0008970.0138951572-0.08667-0.0008290.0147961886.4-0.07348-0.0007610.0178872200.8-0.05526-0.0006580.01994

(a) 升力振幅比例系数

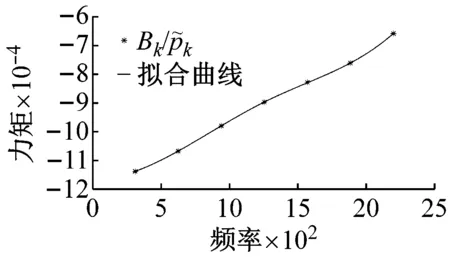
(b) 力矩振幅比例系数

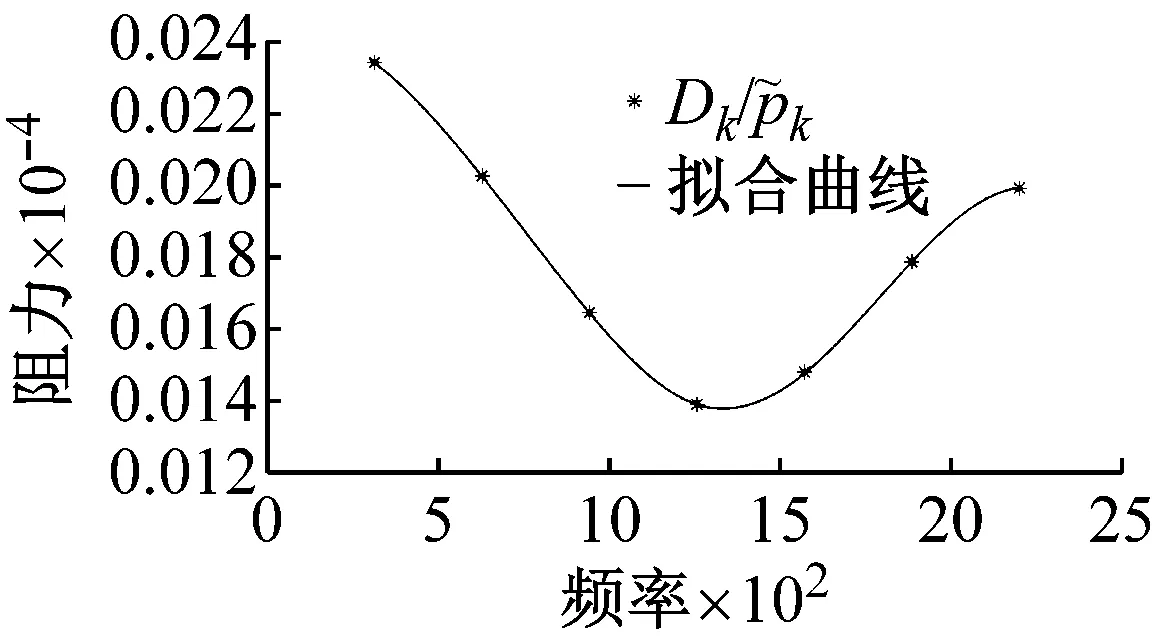
(c) 阻力振幅比例系数

为验证尾流激励的叶片气动力快速分析模型方法和以上拟合曲线，计算一个尾流压力波动下的叶片气动力加以验证。假设已知尾流压力波为：

p=120 300+1 000cos(600t)+

1 000cos(1 200t)+1 000cos(1 500t)

表4 已知尾流各频率对应的振幅比例系数

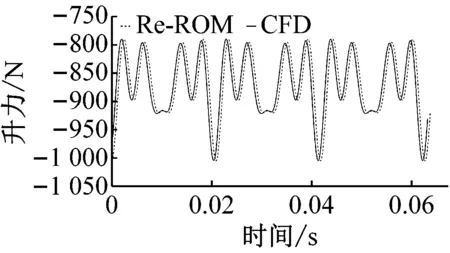
(a) 尾流p激励下的叶片升力

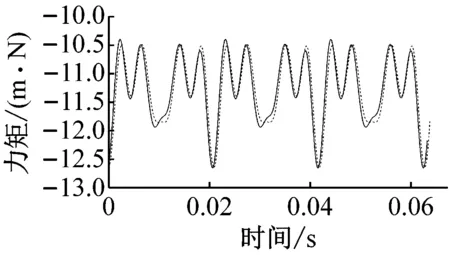
(b) 尾流p激励下的叶片力矩

(c) 尾流p激励下的叶片阻力

从图9中可知：用尾流激励的叶片气动力再降解模型方法计算得到的叶片气动力结果与CFD结果一致。因此，本文提出的尾流激励的叶片气动力快速分析方法是可行的。且对于不同频率的尾流该方法无需用CFD反复计算各谐波下叶片气动力。

3 结 论

本文基于基于谐波平衡法建立了尾流激励的叶片气动力降阶模型方法。算例结果表明：本文提出的尾流激励的叶片气动力降阶模型方法可以快速计算尾流激励下的叶片气动力。

在该尾流激励的叶片气动力降阶模型的公式推导过程中，发现小扰动情况下叶片气动力谐波振幅与尾流谐波振幅的比例系数是关于尾流频率函数。基于此，本文进一步提出了尾流激励的叶片气动力再降阶模型方法，且该方法无需反复的CFD气动力计算。算例的结果表明：再降阶模型方法可以准确估计任意尾流激励下的叶片气动力。