一种流水线ADC及其非理想特性的行为级建模设计
王晓岚,王海晖
(1.天津渤海职业技术学院,天津 300402; 2.武汉工程大学,武汉 430205)
0 引 言
模拟/数字变换器(Analog to Digital Converter,ADC)和数字/模拟变换器(Digital to Analog Converter,DAC)在数字处理核心与外部实际模拟接口中发挥了重要的作用。ADC的应用随处可见,从成像到超声以及通信系统。近年来,特别是流水线ADC结构[1-5]在变换率、分辨率和功耗之间提供了很好的平衡。
传统上,模拟和混合信号模块如数据变换器的建模设计已经在设备级或在更低的功能级得到了实现,提供了很好的精度,并允许对数据变换器中出现的非理想效应(噪声、失真、失配等)能很好地建模,但是仿真时间会急剧增加,技术和架构的独立性可能会丢失;然而,随着设计复杂性的日益增加,需要精确和快速的模型来适应目前行为级建模趋势的变化。在众多方法中,所谓的“行为级建模”可以再现原始分析系统所要求的行为特征。这种方法的目的是得到一种分析和综合模型,这种模型关注底层物理特性,并从而建立起合适的数学概念。
行为级建模采用每个模块的数学特征来描述整个流水线ADC的行为。它可以在速度和精度之间实现最好的权衡,因为预先计算的、参数化的闭合形式的表达式取代了状态方程,用来捕捉模拟模块的动态特性。嵌入到这些闭合形式的表达中的非理想因素以及包含这些非理想因素的影响分析越多,则行为级模型就越好[6-13]。
致力于流水线ADC行为级建模领域的研究通常采用不同高级语言和可替代方法如Matlab Simulink、VHDL-AMS和Spice。事件驱动的行为模型最初用来支持流水线ADC的设计[6-9]。然而,这些早期模型存在一些缺点,即它们大多只考虑少数误差来源。
本文主要针对流水线ADC的行为级进行建模设计,采用目前流行的Matlab Simulink环境来实现。首先,提出了一种采用开关电容器(Switched Capacitor,SC)电路构建的流水线ADC的建模设计,它由一个任意k级级联、前端采样保持(Sample-and-Hold,S/H)电路以及数字校正逻辑构成;然后提出了构成流水线ADC的各个模块电路模型,并这些电路模型构建模块的非理想特性进行了分析和建模,如采样抖动、噪声和运算放大器参数(白噪声、有限直流增益、有限带宽、转换速率(Slew Rate,SR)和饱和电压)等;仿真实验表明,本文提出的流水线ADC的行为级建模设计及其各个构成模块的非理想特性建模是精确和可行的。
1 流水线ADC的行为级建模设计
本文提出的流水线ADC建模设计采用开关电容器(Switched Capacitor,SC)电路构建,它主要利用CMOS的电荷存储能力来实现精确的信号处理,本文提出的流水线ADC结构框图如图1(a)所示。它由任意级联的k级流水级、前端采样保(Sample-and-Hold,S/H)电路和数字校正逻辑构成。级联中的每个流水级实现部分码字长度ni,i=1,…,k,这些码字在数字校正模块被全部重新排列和组合,从而得到变换器的输出;一个流水级的内部结构由4个模块构成,如图1(b)所示。一个有Ni≤2ni个输出码字的闪存子ADC、一个有Ni个输出电平的子DAC、一个减法器和一个增益为Gi的S/H残值放大器。后3个模块在实际设计中是由一个单支电路(通常称为乘法型数字/模拟变换器,Multiplying Digital to Analog Converter,MDAC)来实现。我们把子ADC模块和MDAC模块组合在一起得到一个单一的流水线级。
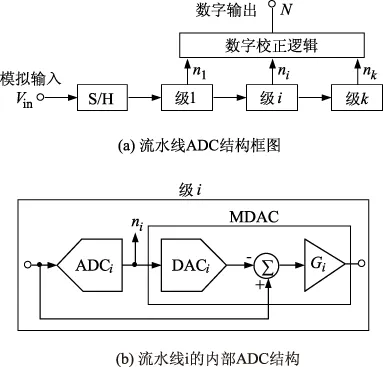
图1 本文提出的流水线ADC构成
1.1 S/H电路
S/H电路采样模拟输入,然后保持输入一定时间的稳定,以便可以被使用。采样电容器(Cs)首先存储采样输入信号,然后将信号电荷传输到反馈电容器(Cf),S/H电路的构成如图2所示。在这种结构中,只有1个电容器用作为采样和反馈,可以实现高速,因为反馈系数(反馈电容与求和节点上的总电容之比)可以更接近于1。S/H的输出电压为:
Vout=1×Vin
(1)

图2 S/H电路
1.2 MDAC
MDAC是一个单一的开关电容器电路,它还可以实现S/H操作、D/A变换、减法和残值放大的功能,MDAC电路构成如图3(a)所示,这种结构的理想行为模型如图3(b)所示。

图3 MDAC电路
根据电荷守恒原理,保持阶段的输出为[14]:
(2)
式中Cs为采样电容;Cf为反馈电容;VDAC是MDAC中子DAC电路的输出电压。
1.3 子ADC和DAC
图4(a)所示为子ADC和DAC的结构框图。子ADC由2个比较器构成,比较器的参考电平最佳设置在+Vref/4和-Vref/4。ADC有一个编码电路将来自于比较器锁存输出的码字转换成二进制代码。每个子ADC级给出2位最高有效位(Most Significant Bit,MSB)和最低有效位(Least Significant Bit,LSB),只用3个有用码字00、01和10来描述由2个比较器构成的3电平ADC;最后,DAC把子ADC的数字信号转换回模拟信号VDAC。子ADC和DAC的行为模型如图4(b)所示。
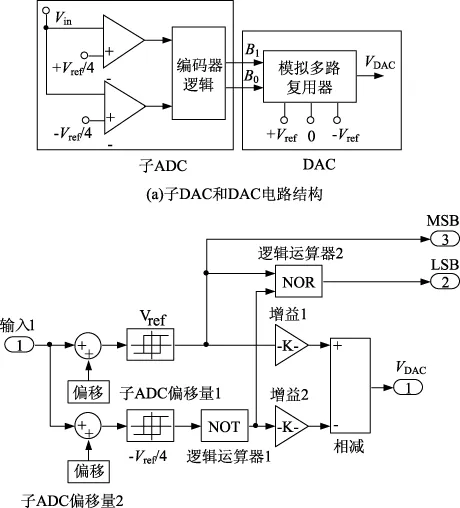
图4 子ADC和DAC电路
1.4 数字校正逻辑
在流水线ADC变换器中,数字电路实现数字误差校正功能是通过将每一级的二进制结果组合为最后的N位二进制数来实现的。它包含延迟逻辑和校正逻辑。延迟逻辑部分由用于建模同步数字电路功能的延迟元件构成。每一级的输出是一个给定的延迟模块,其中第一级有更多的延迟,而最后一级有更少的延迟。数字校正逻辑的行为模型主要由一个全加器构成,包括纹波进位加法器和一个异或(XOR)门。在10位流水线ADC中,在输出端采用数字校正技术得到16位(每级2位,共8级)和10个有效位。
2 流水线ADC的非理想特性分析及其建模设计
这部分主要讨论流水线ADC中的非理想特性及其建模设计。这些非理想特性包括运算放大器的非理想特性(白噪声、有限直流增益、有限带宽、转换速率和饱和电压)、SC开关的非理想特性和采样时钟抖动等。
2.1 运算放大器的非理想特性
一个SC流水线ADC的主要组件是MDAC,它由一个运算放大器构成。一个理想运放有一个无限大的直流增益和无限大的带宽,没有转换速率和饱和限制。
2.1.1非线性运算放大器的直流增益
从理论上讲,运算放大器的直流增益为无限大,理论上的传递函数为:
VoutA0×Vin
(3)
式中Vin和Vout分别为运放的差分输入和输出电压,A0为放大系数。理论上,A0非常大,接近于无穷大,且与频率信号振幅无关。但实际的开环增益A是受电路系统参数约束,而且取决于其输出,故传递函数可近似为[15]:
A≈A0×(1+α1|Vo|+α2|Vo|2+α3|Vo|3+…)
(4)
式中Vo表示SC运放的输出,(α1,α2,α3,…)构成一组寄生非线性放大系数。
实际增益通常是有限的和非线性的,这就导致流水线ADC的非线性。考虑了运放的有限直流增益影响的SC电路(S/H或MDAC)的传递函数成为[8]:
(5)
式中G是SC电路的理想增益,圆括号内的项表示增益误差因子,其中的A是运放的实际直流增益,β为反馈系数。
2.1.2带宽和转换速率
有限带宽和转换速率的影响是彼此相关的,而且可以理解为一个非线性增益[15]。阶跃响应有典型的沉降特性。在初始沉降期,输出信号的斜率受运放的SR限制。一旦输出信号的斜率小于SR,响应进入线性模式。时间转换点在t0。我们把沉降误差行为添加到式(3),此时响应为:
(6)
(7)
必须考虑2种不同情况:
(1)由式(7)得到的值小于运放的SR,这时,没有SR限制,而且Vout的变化遵循式(6);
(2)由式(7)得到的值大于运放的SR,运放处于回转模式。因此,Vout的瞬态响应的第一部分受SR限制,而另一部分将在t0后回到线性沉降模式行为,即:
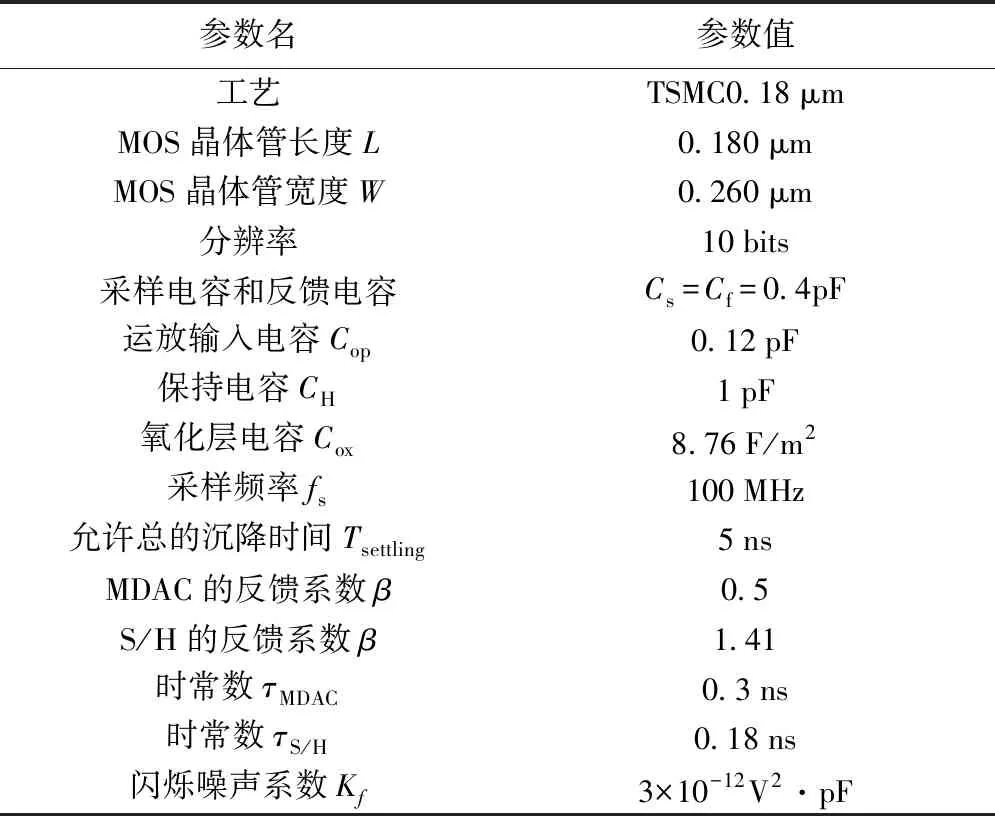
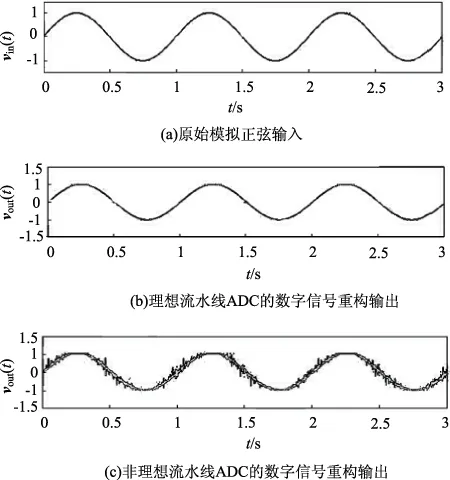
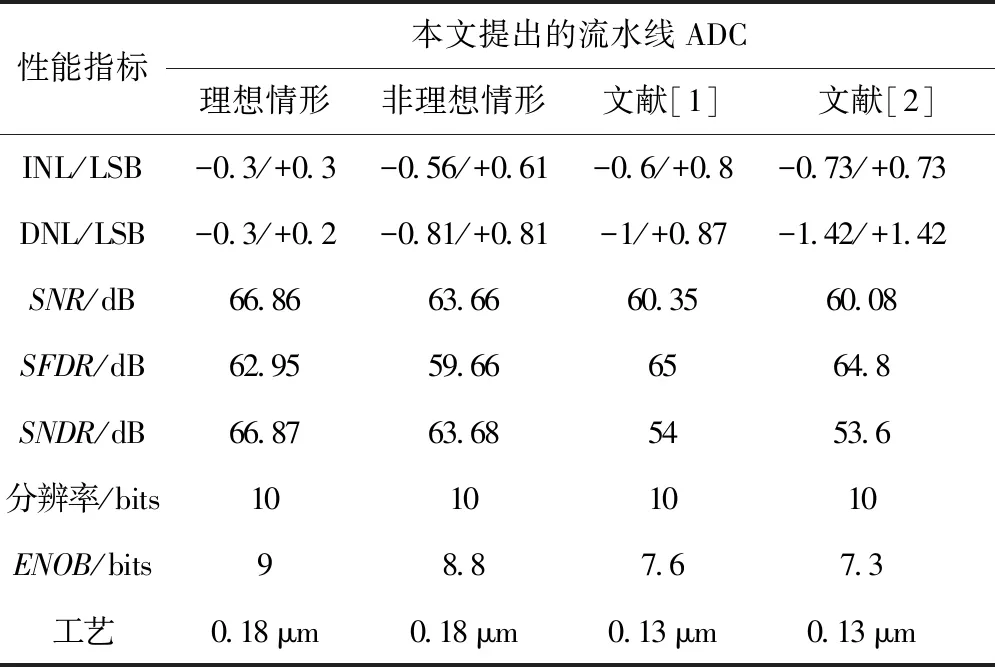
Vout=SR×tt (8) Vout=Vout(t0)+(VinG-SR×t0)× (1-e-(t-t0)/τ)t>t0 (9) 在t0时给式(8)和(9)施加导数连续性条件,得到: (10) 如果t0≥Ts/2,则式(8)对整个时钟周期成立,得到总的沉降时间为: (11) 式中fs=1/Ts为采样频率;Ts为采样周期。 2.1.3运放热噪声 运算放大器的固有热噪声是最重要的噪声源,它影响开关电容MDAC和S/H的运行。运放热噪声的计算与运放结构有关。首先假设噪声源只包括由差分对中的输入晶体管产生的噪声。图5所示为用于计算运放噪声的等效交流模型。 图5 运放噪声计算的等效交流模型 该模型的传递函数为: (12) 式中β为反馈系数;in为噪声电流源;CLT为总负载电容,且CLT=CL+β(Cs+Cop);CL为负载电容;Cop为运放的输入电容;gm为MOSFET的跨导。 噪声电流源可以写成: (13) 式中γ=2/3为长沟道晶体管的系数;K为玻尔兹曼常数;T是绝对温度;f为频率f时的带宽增量,则输入参考噪声功率可以表示为: (14) 式中G为MDAC的增益,S/H和MDAC中的运放是相同的,唯一不同的是在S/H中只有1个采样和保持电容,而在MDAC中有2个电容Cs和Cf,如图3(a)所示。因此,如果令式(14)中的Cs和β分别为0和1,就很容易得到S/H的输入参考噪声;β=Cs/(2B×Cs+Cop),CLT=CL+β(Cs+Cop),B为每级的分辨率。 2.1.4闪烁噪声 对于变换器设计的另一个主要噪声源是闪烁噪声。闪烁噪声或称1/f噪声(其噪声谱密度有一个1/f频率依赖关系)的出现是由于硅氧化物界面的俘获和去俘获效应。噪声电压大致可以用频率f表示为: (15) 式中Kf为闪烁噪声系数,Cox是氧化层电容,W和L分别为MOSFET晶体管的宽度和长度。 2.1.5运放的输入偏移 有2种基本形式的偏移,它们对ADC传递函数有不同的影响。首先,输入偏移与输入信号一起加入到输入级,这种偏移主要由放大器和开关引起。这时的传递函数形式为: Vouti=Gi(Vini+Voffi)-Di×Vref (16) 式中Voffi为输入电压的偏移量;Gi和Vini分别为MDAC电路的增益和输入信号;Di是一个整数,它依赖于子ADC的输出;Vref为参考电压。 第二种形式的偏移量是由于比较器的作用,它可能对ADC的判决电平的1个或2个有影响。来自于全部源的总偏移量必须保持在Vref/4范围内。 2.1.6电容失配误差 电容失配误差影响传输特性。包括电容失配误差的ADC级的总的传递函数为: (17) (18) 式中i是级数;N是位数。不等式(20)表明,电容失配误差在前端是很低的,但在更高的级时分辨率更高。 2.2.1开关噪声 图6 采样开关及其噪声等效 (19) 基带噪声功率由全部折叠频带的噪声功率的积分给出。因此,当开关断开时,存储在Cs上的总噪声功率为: (20) 式中f-3dB=πRsCs/2,Rs为MOS管的表面电阻;Cs为采样电容值,而且电阻被建模为一个噪声源。MDAC和S/H放大器的总输入参考噪声功率分别由式(21)及(22)给出: (21) (22) 式中Cop为运放的输入寄生电容。从式(21)和(22)明显看出,S/H的采样电容Cs,MDAC的电容Cs,Cf和输入电容Cop对ADC的输入参考噪声功率有较大影响。 2.2.2非线性导通电阻 在SC电路的实际实现中,MOS开关的导通电阻对电路的稳定时间有很大的影响。非线性导通电阻依赖于开关电阻信号的变化,会引入谐波失真到电路中;此外,一个由有限开关导通电阻(R)和采样电容(C)构成的单极系统决定了SC电路的输入信号带宽,图7所示为MOS S/H电路和它的MOS开关中的电阻噪声计算的等效模型。采样输入电压为: (23) 式中τ=RC。 图7 S/H电路及其噪声计算的等效模型 抖动定义为采样时刻的随机变化。时钟发生器相位噪声和采样电路是抖动的成因。抖动引入的噪声可以认为是白色的,即在频率0~fs/2之间是均匀分布的。通过过采样输入信号可以减小抖动误差。采样信号的时钟抖动值表示为: x′i(t)=xi(t)+δ×[xi(t+1)-xi(t)]×fs (24) 式中x′i(t)为由采用实际采样频率fs时样本值xi(t)中的抖动偏移量δ引起的误差。采用泰勒级数展开有[16]: (25) 时钟抖动导致一个非均匀采样时间序列,并产生一个误差,这个误差增大了整个流水线ADC的频谱输出的总误差功率。当一个幅值为A、频率为fin的正弦信号x(t)在一个时刻被采样时,由抖动偏移量δ引起的误差为: (26) 这里假设δ是一个标准偏差为τ的高斯随机过程。 为了评价本文提出的流水线ADC的建模设计以及各种非理想因素对流水线ADC运行的影响,我们针对10位分辨率理想和非理想特性的流水线ADC建模设计在Matlab Simulink中进行仿真,仿真实验参数如表1所示。通过将数字输出重构为原始形式来进行验证,原始输入形式采用正弦波输入。 表1 10位流水线ADC的仿真参数 图8所示为原始模拟正弦输入以及理想和非理想流水线ADC建模设计重构的2个数字输出波形,图9为重构输出的FFT(Fast Fourier Transform)。 图8 原始模拟正弦输入和重构后得到的输出 图9 2种情况下fin=1.78 MHz, fs=100 MHz时重构输出的FFT 从图8和9可见,正如前面所分析的,尽管ADC的非理想特性对流水线ADC建模设计的输出信号有影响,但本文提出的建模设计也能够得到与理想情况下流水线ADC建模设计非常接近的重构输出,而且谐波频谱明显降低,说明本文提出的流水线ADC建模设计是稳定和精确的。 表2所示为对本文提出的流水线ADC在理想和非理想情形下以及与文献[1]、[2]提出的流水线ADC的仿真结果比较。表中比较的性能指标包括微分非线性(Differential Non-Linearity,DNL)和积分非线性(Integral Non-Linearity,INL)、信噪比(Signal-to-Noise Ratio,SNR)、信号噪声失真比(Signal-to-Noise and Distortion Ratio,SNDR)、无杂散动态范围(Spurious-Free Dynamic Range,SFDR)、分辨率、有效位数(Effective Number of Bits,ENOB)和工艺。 从表2可以看到,当包括时钟抖动、开关管热噪声和运放非理想特性(有限增益、有限带宽、转换速率和饱和度)噪声源加入到ADC建模设计中时,各项性能指标比理想时略有降低,这是符合实际情况的,与前面的信号重建仿真结果是相吻合的;但本文提出的非理想流水线ADC(即考虑各种非理想特性后)的建模设计相比于文献[1]、[2]提出的流水线ADC设计在各种性能上更优,说明本文提出的流水线ADC及其非理想特性建模是实际可行的。 表2 各种ADC的性能比较 本文提出了一种中等分辨率的流水线ADC结构的设计,并在Matlab Simulink中对其理想和非理想模型进行了验证。结果表明,本文提出的设计模型在行为级考虑大多数流水线ADC的非理想特性如采样抖动、噪声和运放参数(白噪声、有限直流增益、有限的带宽和转换速率等)等是符合实际的,采用适当的设计环境,只需定义适当的输入激励,就可以完成输出数据特定的处理,能快速实现任何数据变换器结构的行为描述。
2.2 开关的非理想特性
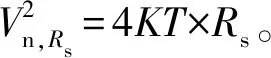
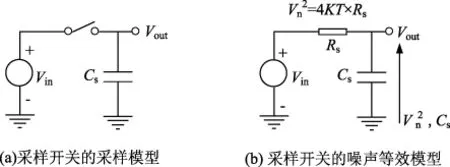
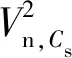

2.3 采样时钟抖动
3 仿真实验结果

4 结 语

