棉秆起拔力关键因素的研究及试验
陈佳林,曹肆林,卢勇涛,王 敏,营雨坤
(1.石河子大学,新疆 石河子 832003;2.新疆农垦科学院,新疆 石河子 832003)
0 引言
棉花是世界上最重要的农作物之一。在我国,植棉历史悠久,种植技术成熟,棉花产量约占世界棉花产量的1/4。棉花在采摘时产生大量的副产物[1-2],但主要产棉区对棉秆利用效率低,造成了资源的浪费[3]。棉秆作为棉花产业的副产品,是一种重要的可再生生物质能源,可作为反刍家畜的饲料,也可用于造纸、制板、食用菌培养、环保材料、化学制品、秸秆炭及建筑材料等,具有巨大经济效益。据统计,我国棉花种植面积为600万hm2,每年棉秆的产量约为3 000万t,若将这些棉秆用于制造纸张,每年可以节省林木资源12万m3,与此同时,每100万t棉秆,产生的经济效益为10亿元。目前,棉秆收获技术发展迟缓,配套收获装备性能低下,未能得到广泛推广。除新疆地区大部分棉秆被粉碎还田外,其他地区多数农户仍旧采用手工拔除或焚烧的方式处理,致使棉秆资源利用率低下。拔秆收获能实现棉秆的收集,可避免残留根茬对下一轮作物的不利影响,所以非常受农户的欢迎。我国传统的拔棉秆方式不仅费时费力,且效率低下,若采用机械拔取棉秆,在减轻棉农劳动强度的同时,也可增加一定的经济收入。由于棉秆主茎粗细不一致,土壤吸附力大,人工收获劳动强度大、耗功大,开展棉秆机械收获技术研究已成为近年来棉花生产全程机械化技术研究的重点之一[4-9]。
通过对试验田的进一步考察分析后,进行了起拔力的测试试验,并对试验田的测量数据进行了分析,研究了各因素对起拔力的影响规律,以期为棉秆起拔机械的设计提供数据参考。棉秆直径对起拔力有较大的影响,设计棉秆起拔机时最大起拔力可以参考棉秆直径进行设计。其中,土质、土壤含水量和土壤坚实度对棉秆的起拔力有一定的影响,合理地选择收获时间,可以减少动力的消耗,有效提高起拔效率。
1 材料与方法
1.1 试验材料
2017年10月,在新疆农垦科学院试验田实验基地进行试验。新疆气候干燥少雨,冬季寒冷且长。试验田的棉秆品种为华农16号,株距12cm,行距为(60+10)cm,数据采集区的棉花采用1膜6行的种植模式。棉秆试样按照生长良好、茎秆直挺、粗细均匀的基本原则进行选取[10-11]。
1.2 试验方法
数据采集从棉花收获后开始,一共选取5块试验田的5个作业段,每个作业段选取20个样本进行试验,主要采集棉秆起拔力、棉秆直径、土壤含水率、土壤坚实度和棉秆高度等数据。
1)棉秆起拔力的测定。棉秆起拔力的测量使用温州市海宝仪器有限公司HF-1000型数显式推拉力计(量程0~1 000N,精度0.05N),其能够通过显示屏显示测量力的不断变化,当将工作模式设置为Peak(峰值保持)模式时,就会把每次测量的最大数据自动保存,并存储。具体测量方法是:用尼龙绳一端系在棉秆的底部,另一端连接到推拉力计上,然后缓慢地起拔,当根部完全脱离土壤后,读取并记录下最大数据,如图1所示。每个作业段测量20组数据,最后形成棉秆直径、棉秆高度、起拔阻力、棉秆是否拔断、土壤坚实度和土壤含水率的数据表格,后求取各组因数的平均值,并且列出其大小范围,经处理后如表1所示。
2)棉秆高度的测定。每株棉秆从其地上根茎部分到主秆顶端为测量的高度部分,用卷尺(精度1mm)测量并同时记录下读数,对同一块试验田选取20 个样本。
3)棉秆直径的测定。以棉根底部为基准,每向上10cm测量1次,一共向上测量3次,用游标卡尺(精度0.02mm)进行测量,并取其平均值近似为棉秆直径。对同一块试验田选取20 个样本。

图1 棉秆起拔力测定

作业段棉秆直径/mm直径范围平均值棉秆高度/cm高度范围平均值起拔阻力/N 阻力范围平均值平均土壤含水率/%平均土壤坚实度/kPa17.93~12.509.7171.1~95.284.83360.3~776.7500.1617.09423.327.94~14.819.9467.8~99.481.57378.5~726.1473.6218.44387.537.67~11.7511.7561.2~92.669.62289.4~821.1539.4916.65449.947.98~11.959.8564.2~93.278.60234.7~796.9489.7116.54398.658.02~12.849.6262.3~99.881.15160.1~999.3512.5416.89450.0
4)土壤含水率和紧实度的测定。土壤坚实度的采集采用SC900数字式土壤坚实度仪(程0~7 000kPa,精度0103kPa),测量时将其探头缓缓插入土壤10cm处深度,然后读取数值。土壤含水率的采集采用TDR 300土壤水分仪(范围0-饱和状态,精度3.0%体积水含量),测量时将其探头缓缓插入土壤10cm处深度,然后读取数值,如图2所示。测量点选取在地段中间,每次测量的选点与所测量的其它参数一一对应,每个作业段选取10个点,然后取其平均值。对同一块试验田选取20 个样本。
2 结果与分析
本文将对所测数据用MINITAB软件进行散点图图形处理及拟合,然后对5组数据进行线性回归分析。

图2 土壤坚实度测定
2.1 棉秆直径对起拔力的影响
由于棉秆起拔力受多种因素影响,结合已有研究,确定以棉秆直径为影响因素对棉秆起拔力进行单因素试验研究。为了进一步分析研究结果,文中选取第2、3、5组采样数据进行了线性回归分析,分析结果如图3所示。

○代表第2组采样数据 +代表第3组采样数据 △代表第5组采样数据
线性回归模型为
y2=87.9+38.8x
S=42.16,R-Sq=69.2%,P=0
因P<0.05,可知线性回归模型成立;R-Sq=69.2% ,说明回归方程显著性一般。
y3=-609+120x
S=86.96,R-Sq=73.0%,P=0
因P<0.05,可知线性回归模型成立;R-Sq=73.0%,说明回归方程显著性一般。
y5=-418+96.6x
S=189.49,R-Sq=35.1%,P=0.006
因P<0.05,可知线性回归模型成立;R-Sq=35.1%,说明回归方程不显著。
根据MINITAB软件的分析,可以直观地看出:在同一个作业段的采集数据中,棉秆的起拔力与棉秆直径成正相关关系,起拔力具有随棉秆直径的增大而增大的趋势,如图3所示。线性回归分析得出的3组处理结果中P值均小于0.05,这表明线性回归模型是成立的;但回归模型y2中的R-Sq=69.2%和y3中的R-Sq=73.0%,说明其模型线性回归性不显著。而回归模型中y5的R-Sq=35.1%,说明其模型线性回归极不显著。这种情况是由于棉秆起拔力的影响因素可能与土壤的坚实度、含水率、棉秆起拔的角度及棉秆根系的分布生长情况等有关。在同一块作业段中,由于施肥不均等因素,造成棉秆根系生长不同,还有土壤坚实度和含水率的不均匀性等导致了棉秆起拔力存在较大的差别,因此这只反应了一定情况下棉秆直径与起拔力的关系。
2.2 棉秆高度对起拔力的影响
由于棉秆高度与棉秆起拔力并没有直接的关系,根据上文得出了棉秆直径与起拔力成正相关关系,因此笔者对棉秆直径与棉秆高度的关系进行了分析。文中选取了第1、2、3组采样数据进行线性回归分析,分析结果如图4所示。
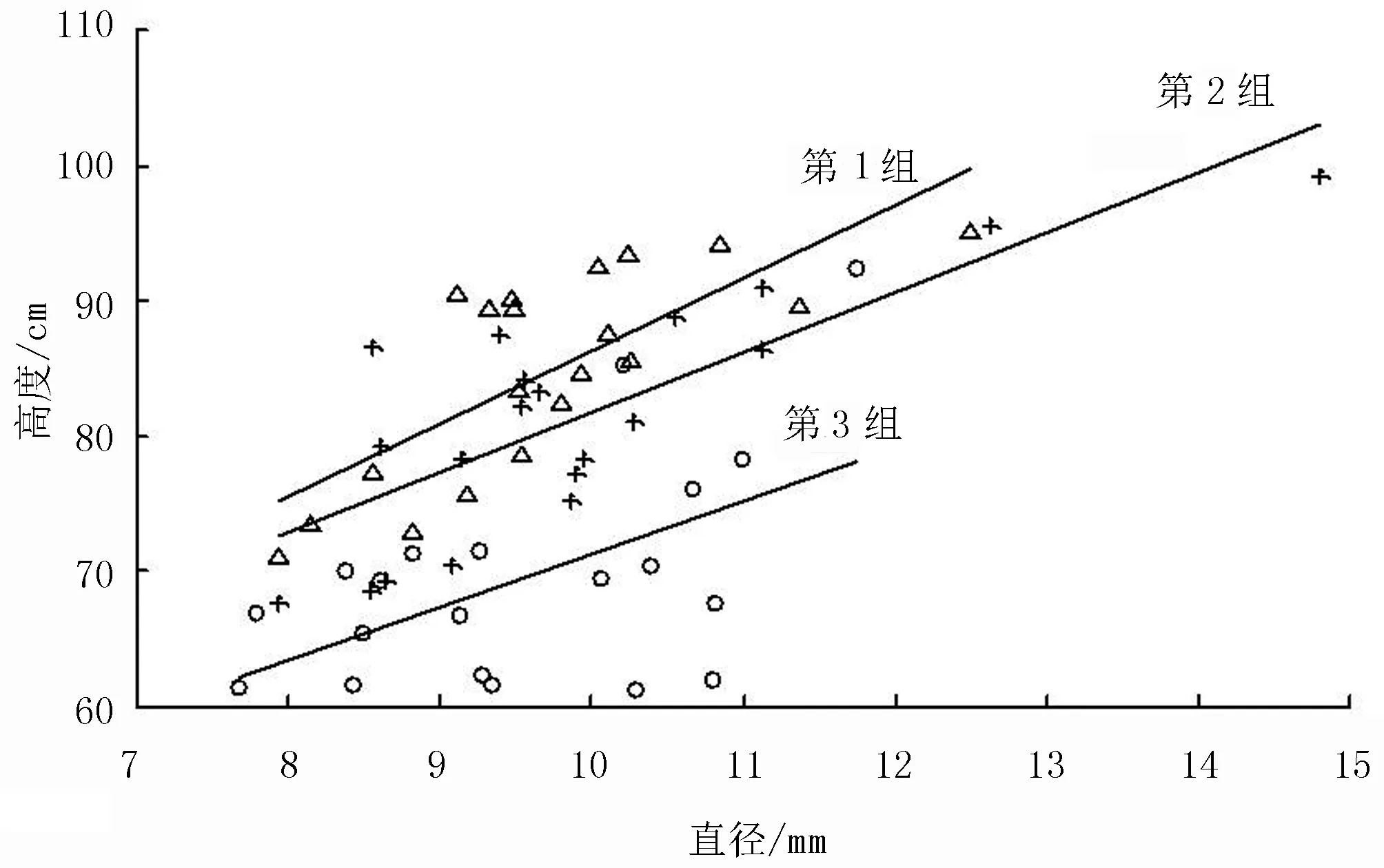
○代表第3组采样数据 +代表第2组采样数据 △代表第1组采样数据
线性回归模型为
y1=32.2+5.42x
S=5.18,R-Sq=56.7%,P=0
y2=37.5+4.43x
S=5.45,R-Sq=63.6%,P=0
y3=32.3+3.91x
S=7.17,R-Sq=29.6%,P=0.013
对y1、y2、y3回归方程进行分析:在y1与y2的回归模型中,P=0<0.05,可知线性回归模型成立;y1中R-Sq=56.7%,y2中R-Sq=63.6%,说明回归方程显著性一般;在y3的回归模型中,P=0.013<0.05,可知线性回归模型成立;R-Sq=29.6%,说明回归方程不显著。
根据MINITAB软件的分析,可以直观地看出:在同一个作业段的采集数据中,棉秆的高度与棉秆直径成正相关关系,棉秆高度具有随棉秆直径的增大而增大的趋势,如图4所示。线性回归分析得出的3组处理结果中P值均小于0.05,表明线性回归模型是成立的;但回归模型中y3的R-Sq=35.1%,说明其模型线性回归极不显著。这是因为棉秆的生长可能受温度、光照、肥料和水分等因数的影响,在同一块作业段中,由于施肥的不均匀性和棉秆吸收的差异,造成了棉秆的大小不同。根据上文得出的结论:棉秆直径与起拔力成正相关关系,因此推出棉秆起拔力与棉秆高度成正相关关系。
2.3 土壤含水率对起拔力的影响
对棉秆起拔力与土壤含水率进行了单因素研究,将5个作业段的数据一一对应进行了线性回归分析。
线性回归模型为
y=1064-33.6x
S=120.77,R-Sq=37.7%,P=0
因P<0.05,可知线性回归模型成立;R-Sq=37.7% ,说明回归方程不显著。
棉秆起拔力与土壤含水率的关系如图5所示。棉秆起拔力与土壤含水率呈负相关关系,起拔力具有随土壤含水率的增加而减小的趋势。
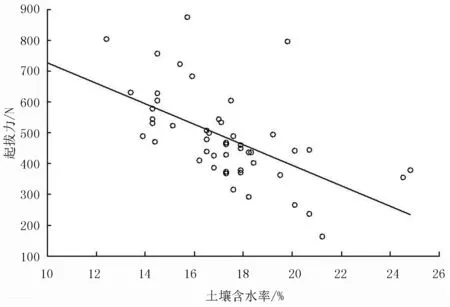
图5 棉秆起拔力与土壤含水率的关系
2.4 土壤坚实度对起拔力的影响
对棉秆起拔力与土壤坚实度进行了单因素研究,将5个作业段的数据一一对应进行了线性回归分析。
线性回归模型为
y=-88+1.37x
S=119.22,R-Sq=39.3%,P=0
因P<0.05,可知线性回归模型成立;R-Sq=39.3%,说明回归方程不显著。
棉秆起拔力与土壤含水率的关系如图6所示。棉秆起拔力与土壤含水率呈正相关关系,起拔力具有随土壤坚实度的增加而增大的趋势。
3 结论
1)在同一个作业段中,棉秆直径是影响起拔力的关键因素,棉秆直径与起拔力成正相关关系。在采集的5组数据中,第5组棉秆直径最大值为12.84mm,最大起拔力为993.3N。在设计棉秆起拔机时,最大起拔力可参考棉秆直径进行设计。棉秆起拔力与棉秆高度成正相关关系;棉秆起拔力与土壤含水率呈负相关关系;棉秆起拔力与土壤坚实度呈正相关关系。在已采集的5个作业段的数据中,第3组棉秆起拔力最大,单株棉秆最大起拔力为821.1N,平均起拔力为534.49N;第2组棉秆起拔力最小,单株棉秆最大起拔力达到726.1N,平均起拔力为473.62N。棉秆起拔力的大小受土壤含水率、坚实度的影响很大,因此应选取合适的季节拔秆,以减小动力消耗,提高效率。
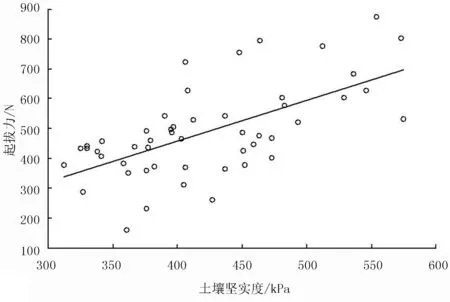
图6 棉秆起拔力与土壤坚实度的关系
2)棉秆的起拔力是棉秆收获需要考虑的主要因素之一。在本试验中,仅在第4作业段中拔断了1根,土壤含水率和土壤坚实度不同棉秆的力学性能就不同。尽管作业段4中拉拔阻力较小,但棉秆的抗拉强度和抗弯强度等力学特性参数也较小,极易在拔秆作业中发生断裂[12],因此拔秆时需综合考虑。本试验所测数据及线性回归方程更适合于新疆地区。

