棉秸秆力学特性和拉拔阻力研究
汪珽珏,陈明江,张佳喜,王振伟,赵维松,曲浩丽
(1.新疆农业大学 机电工程学院,乌鲁木齐 830052;2.农业部南京农业机械化研究所,南京 210014)
0 引言
棉花的种植在我国已有2 800年的历史,人工种植的区域主要分布在长江流域、黄河流域及西北内陆地区[1-3]。棉花产业会产生很多副产品。棉秆是棉花的主要副产品。我国2017年棉花播种面积3.2296×1011m2(4844.5万亩),按照单产秸秆300kg/667m2计算,全国每年棉秆产量约为1 453万t。如果这样大量的资源实现循环利用,将产生巨大的经济效益。目前,棉秆的机收率还比较低,主要原因包括整秆收获较为困难、拔取回收机械研究欠缺及机械化原理研究不透彻[4-5]。
开展棉秆的机械物理特性试验研究,获得其机械物理特性,可为分析棉秆收获过程中应力、应变分布状态、确定棉秆起拔方式等提供理论依据和技术参数,对棉秆的高效收获机具的设计有重要的指导意义[6-9]。国内外对于棉秆的研究主要集中在小麦、玉米等的力学性能及收割收获方面,对于棉秆的力学综合性能研究并不全面,无法对农机机具的设计提供现实参考意义[10-13]。棉秆的物理性质是秸秆收获和加工的重要参数,主要力学性能为抗弯强度、抗拉强度和拉拔阻力等;物理性质为含水率、秸秆直径等。其中,棉秆的拉拔阻力是棉秆收获机理的重要研究参数,棉秆的物理性质和拉拔阻力直接影响棉秆的收获和加工成本,对研究棉秆循环利用具有积极意义[14-20]。
1 材料与方法
1.1 试验材料与设备
试验地为山东省滨州市无棣县棉花全程机械化示范基地,试验材料为机采棉品种是中棉所50,棉花采用76cm等行距种植,采集时间为2015年10月23日—2016年3月21日,共分6个批次。主要设备有WDW—10型电子万能试验机、TYD—1型土壤硬度计、SH—1000型数显示推拉力计、HN202—2真空烘干箱及游标卡尺等[21-22]。
1.2 试验方法
采用三点弯曲方法,试验测定棉秆在发生破坏时的最大载荷,试验方法参考《GB/T 1936.1—2009木材抗弯曲强度试验方法》;拉伸试验参考《GB/T 1938—2009 木材顺纹抗拉强度试验方法》;棉秆相对含水量的测定方法参考《GB/T 1931—2009木材含水量测定方法》。棉秆起拔力测定的具体方法为:用尼龙绳一端拴在棉秆的根部,另一端连接到推拉力计的挂钩上,并竖直向上缓慢提拔,根部脱离土壤后,读取最大数据[23-27],如图1所示。

图1 棉秆起拔力以及力学特性测量Fig.1 Cotton rod pull-out force and physical properties measurement
1.3 处理方法
利用统计分析软件SAS 9.3进行统计分析,通过典型相关性分析棉秆的力学特性和物理性质的关系,并采用多元回归分析棉秆起拔力与棉秆物理性质的关系[27-31]。
2 结果与分析
2.1 棉秸秆物理特性以及起拔力的描述统计
2.1.1 棉秸秆物理特性统计描述
分别对不同批次棉秆的含水率、直径、弯曲破坏载荷、抗拉强度、拉伸破坏载荷和抗拉强度进行试验测试,统计如表1所示。由表1可以看出:随着采样时间的增长,棉秆的含水率逐渐降低,从第1批次到第3批次时棉秆含水率下降较为缓慢,在第3批以后棉秆的含水率下降较快,以每个月超过10%的幅度下降;棉秆的直径在一个稳定的水平,并没有随着采样时间的改变发生较大变化;棉秆的平均抗拉强度随着采样时间的增长逐渐下降,且下降的幅度逐渐变小;棉秆的抗弯强度随着采样时间的增长,总体呈增长趋势。

表1 棉秸秆物理特性指标的总体统计Table 1 Overall statistics of physical characteristics of cotton straw
2.1.2 棉秆起拔力统计描述
对棉秆起拔力及主要影响因素棉秆平均直径、土壤硬度和棉秆含水率进行试验测试,如表2所示。由表2可以看出:棉秆的平均拉拔阻力最大达到670.82N,最小为340.7N。由于在1月份以后土壤已经逐渐发生冰冻,随着气温的下降冻土深度增加,棉秆拉拔阻力急剧增大且寒冬不适合田间作业,棉秆起拔力的收集失去其意义,故未收集相关数据。平均土壤硬度随着时间推移最大达到9.4kg/m2,最小为3.3kg/m2。

表2 棉秸秆起拔力描述统计Table 2 Description and statistics of uplift force of cotton straw
2.2 典型相关性分析
2.2.1棉秆的弯曲力特性与含水率及直径的典型相关分析
对棉秆的抗弯强度、弯曲力、直径和含水率进行典型相关性分析,共得到两组典型变量。典型关联分析如表3所示,相关系数检验如表4所示。
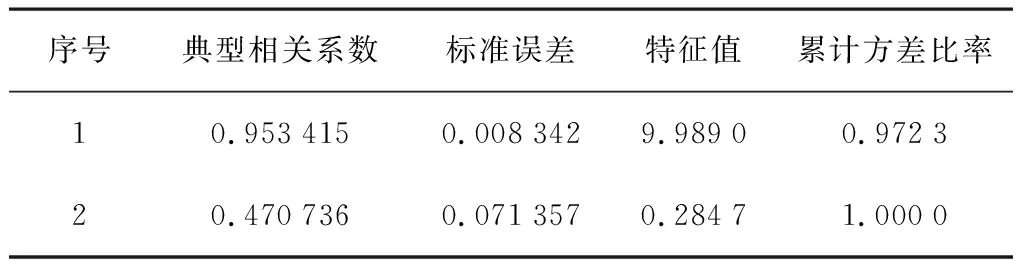
表3 棉秆的抗弯强度与影响因素的相关系数及特征值Table 3 Correlation coefficient and eigenvalue of bending strength of cotton stalk and its influencing factors
由表3、表4可以看出:两组典型变量都极为显著。因此,选择两组典型变量进行分析,得出棉秆的弯曲力特性与影响因素的典型相关模型,如表5所示。
从建立的典型相关模型可以看出,典型变量的重要程度及系数大小和两个自变量代表的影响组对棉秆的弯曲特性可以用1对典型相关变量予以综合描述。具体体现在如下方面:
1)棉秆直径对棉秆的弯曲破坏载荷起着很大影响。棉秆直径与棉秆的弯曲特性反应在典型相关模型中,v1是棉秆弯曲力与棉秆弯曲强度的线性组合,弯曲破坏载荷的载荷为1.074 3,是弯曲性能中最大的。w1是影响因素指标的线性组合,棉秆直径的载荷为0.979 1,远远超过w1内其他指标的数值。考虑到第1对典型相关变量的相关系数几乎接近于1,可以认为棉秆的直径与棉秆的弯曲破坏载荷有着极大的相关性。通过观察表2可知棉秆直径越大则其弯曲破坏载荷越大,且直径对弯曲破坏载荷的影响远大于含水率对弯曲破坏载荷的影响。
2)棉秆含水率是决定棉秆抗弯强度的关键因素。在第2对典型变量中,秸秆抗弯强度在典型变量v2中的载荷为-0.803 1,是秸秆弯曲性能指标中最大的;而棉秆的含水率在典型变量w2中载荷最大,为-1.027 2。这一对典型相关变量的相关系数非常之高,表明含水率对棉秆的抗弯强度相关性很大,含水率越高,抗弯强度越低。
2.2.2棉秆的拉伸力特性与含水率及直径的典型相关分析
对棉秆的抗拉强度,最大拉伸力、直径及含水率进行典型相关性分析,可以得到两组典型变量他们的典型关联分析如表6所示,相关系数检验如表7所示。
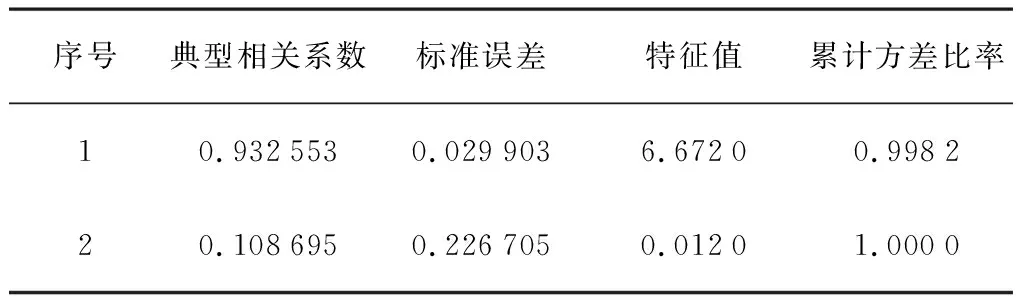
表6 棉秆的抗拉强度与影响因素的相关系数及特征值Table 6 Correlation coefficient and eigenvalue of tensilestrength of cotton stalk and its influencing factors
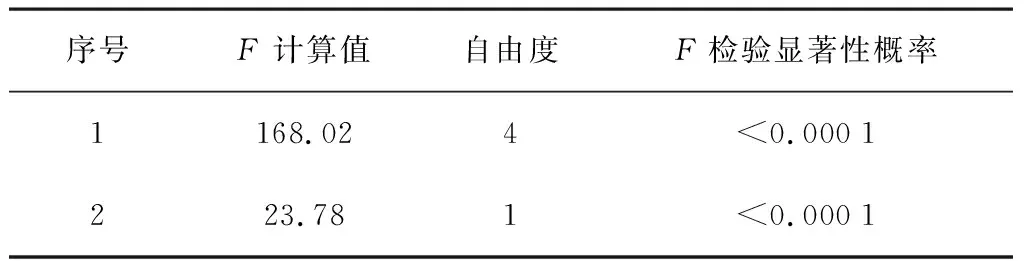
表7 相关系数检验Table 7 Correlation coefficient test
由表6、表7可以看出:两组典型变量极为显著,对两组典型变量进行分析,得到拉伸特性与影响因素的典型相关模型如表8所示。

表8 棉秆的抗拉强度与影响因素的典型相关模型Table 8 Canonical correlation model of tensile strength and influencing factors of cotton stalk
棉秆含水率决定棉秆抗拉强度及棉秆的拉伸破坏载荷。在第2对典型变量中,棉秆抗拉强度在典型变量m2中的载荷为0.559 6;棉秆的最大拉伸力在典型变量中m2的载荷是0.579 4。棉秆的最大拉伸力与棉秆抗拉强度的载荷相近,此处认为棉秆的含水率对抗拉强度及最大拉伸力都有相关性。对比表1可知,都为正相关,即含水率越大,棉秆的抗拉强度越大,棉秆的拉伸破坏载荷越大。
棉秆的直径决定棉秆的拉伸破坏载荷。在第1对典型变量中,棉秆抗拉强度在典型变量m1中的载荷为-1.049 8;棉秆的拉伸破坏载荷在典型变量m1中的载荷是1.039 0。棉秆的拉伸破坏载荷与棉秆的抗拉强度相近,此处认为棉秆的直径对最大拉伸力具有显著相关性,对比表1知棉秆的直径与拉伸破坏载荷呈正相关,即棉秆的直径越大,最大拉伸力越大,且直径对拉伸破坏载荷的影响远大于含水率对拉伸破坏载荷的影响。
2.3 棉秆起拔力与其物理特性的分析
2.3.1 棉秆起拔力分析的方法选择
基于棉秆的直径、含水率、土壤紧实度及起拔力的相关实测数据,采用多元统计中的回归分析方法对棉秆起拔力进行分析。
2.3.2 棉秆起拔力与含水率关系
通过对第1批次、第2批次、第6批次的样本数据进行回归分析,分析结果如图2(a)所示。棉秆起拔力与含水率的线性回归模型为

图2 棉秆拉拔阻力与影响因素的关系Fig.2 Relationship between pulling resistance of cotton rod and influencing factors
y1=17.74325x1+409.40949
(1)
其中,y1为棉秆的起拔力(N);x1为棉秆的含水率(%)。在棉秆含水率与起拔力的回归分析的方程中,回归方程的P值为0.963 8,说明回归模型不显著,棉秆的含水率对于起拔力的大小不会造成影响。
2.3.3 棉秆起拔力与棉秆直径的关系
通过对样本数据进行回归分析,分析结果如图2(b)所示。棉秆起拔力与棉秆直径的线性回归模型为
y2=27.88644x2
(2)
其中,y2为棉秆的起拔力(N);x2为棉秆直径(mm)。在棉秆起拔力与含水率的回归方程中,方程的假定值P≪0.001,说明模型显著。参数x2的P值远小于0.001,但是常数项的P值为0.752 8,舍去。模型的拟合优度为0.346 7,拟合优度偏低。由回归模型可以看出,棉秆的直径与棉秆起拔力呈正相关。
2.3.4 棉秆起拔力与土壤硬度的关系
对棉秆的起拔力与土壤硬度进行回归分析,分析结果如图2(c)所示。棉秆起拔力与棉秆直径的线性回归方程模型为
y3=37.16027x3+244.42547
(3)
其中,y3为棉秆的起拔力(N);x3为秸秆地的土壤紧实度(kg/m)。在棉秆起拔力与棉秆直径的线性回归方程中,模型假定值p=0.001<0.05,说明模型显著。参数x3、常数项的p值(假定值)都符合检验,模型的拟合优度R-Square为0.179 0,拟合优度偏低。由回归模型可以看出,棉秆的直径与棉秆的起拔力呈正相关。
2.3.5 棉秆起拔力多元线性回归分析
多元线性回归是以多个解释变量的给定值为条件的回归分析,是研究一个因变量和多个自变量间的线性关系方法,多元线性回归模型的一般形式为
Y=β0+β1X1+β2X2+…+βiXi+…βkXk+u
其中,k为解释变量数目;βi(j=1,2,k)为回归系数;u为去除k个自变量对Y影响后的随机误差[32-33]。本文以滨州地区2015年10月23日-2016年3月21日采集的6批次棉秆实测得出的棉秆直径、含水率、土壤紧实度及棉秆起拔力作为基础系列数据,利用SAS软件对各变量数据进行一元回归分析得出:棉秆直径和土壤紧实度是影响棉秆起拔力的主要因素,棉秆的含水率对棉秆的起拔力几乎没有影响。
由式(1)~式(3)中能得到符合条件的模型,但是无论是土壤紧实度,还是棉秆半径的模型,其拟合度都达不到理想的效果,不能很好地描述起拔力与棉秆直径及土壤紧实度的关系。引入多元回归,以棉秆起拔力为因变量,棉秆的直径及土壤紧实度为自变量建立多元回归模型,回归方程式为
y4=36.32720x3+27.56728x2
(4)
其中,y4为棉秆的起拔力(N);x3为秸秆地的土壤硬度(kg/m2);x2为棉秆直径(mm)。模型的的假定值P<0.001,故拒绝原假设,接受备选假设,认为y与x3、x2之间具有显著线性相关关系;但是模型拟合优度R-Square为0.517 6,偏低。
由式(4)可知,回归方程显著拟合优度偏低。其主要原因如下:棉秆的起拔力影响因素很多,方程中的影响因素不能全部囊括进来,但棉秆直径及土壤紧实度与起拔力模型能达到50%的拟合度,对于只需大体确定棉秆起拔力范围的拔杆机械具有重要指导作用,所以本文起拔力的影响因素可设为土壤硬度和棉秆直径。
为了提高模型的拟合度,使得模型更加准确,此处引入多元线性回归的回归诊断图,如图3所示。图3中包括残差分析影响分析。根据影响分析图剔除统计样本中的离群点,剔除样本中的离群点后重新对样本进行回归分析,模型为

图3 多元线性分析回归诊断Fig.3 Multiva Multivariate linear regression regression diagnosis
y=-111.73707+45.39254x3+23.89125x2
(5)
分析得出模型及参数p值均显著,且模型拟合优度达到0.81。
2.3.6 回归验证与预测
对回归模型进行验证,2018年3月收集的棉秆的起拔力实际值和预测值的变化情况如图4所示。由图4可知:棉秆的起拔力值和预测值接近。由SAS软件相关分析得出,棉秆起拔力的实际值和预测值相关系数为0.76。上述多元线性回归分析模型适用于棉秆起拔力的预测,对于拔棉秆机的设计具有指导作用。

图4 棉秆起拔力和预测力对比Fig.4 Comparison of uplift force and prediction force of cotton rod
3 结论
1)抗拉强度在含水率最高为61%时达到最大值37.65MPa,当含水率在在15%~50%之间,棉秆的抗拉强度变化不大,平均抗拉强度集中在21.5~25.8MPa之间;对于抗弯强度,在含水率为15%时达到最高值33MPa,当含水率在25%~55%之间时棉秆的抗弯强度变化不大,平均抗弯强度集中在23.5~27MPa之间。
2)对于棉秆起拔力,在土壤紧实度为最低的3.3kg/cm2时达到最小值340.7N,棉秆的起拔力随着土壤紧实度的降低而降低。
3)棉秆的弯曲破坏载荷及拉伸破坏载荷与棉秆的直径和棉秆的含水率都有着显著的相关性,且棉秆直径对弯曲和拉伸破坏载荷的影响远大于含水率对棉秆拉伸和弯曲破坏载荷的影响。
4)棉秆的抗弯强度随着棉秆的含水率增大而减小,棉秆的抗拉强度随着含水率的增大而增大。
5)对棉秆的起拔力与棉秆含水率、棉秆直径及土壤紧实度进行回归分析,发现棉秆的起拔力与棉秆的含水率相关性不显著,棉秆的起拔力与土壤紧实度及棉秆的直径都呈正相关。
6)对棉秆的回归分析进行分析诊断,对棉秆起拔力的多元分析模型进行优化得到棉秆起拔力与棉秆直径及土壤紧实度的模型y=-111.73707+45.39254x1+23.89125x2。其拟合优度为0.81,可以用于对棉秆起拔力的预测及拔棉秆机的设计研究。

