基于热成像的粮食干燥换热器圆桶壁热阻测试
张高杰,车 刚,万 霖,陈竹筠,金中波
(黑龙江八一农垦大学 农业机械化工程重点实验室,黑龙江 大庆 163319)
0 引言
粮食干燥用气相旋转换热器多层圆筒壁结构的热性能是保证换热器内部换热环境的一个重要因素,影响着换热器内部温度的高低,间接地影响着换热器的换热效率[1]。相比于传统的换热器,粮食干燥用气相旋转换热器圆桶为旋转结构,筒壁磨损大,长期的工作会导致筒壁材料热工性能发生变化。如何快速、便捷地测量圆筒壁传热阻值,对设计、使用和维护气相旋转换热器并获得良好的换热效率具有重要的意义。
传热阻值是评价粮食干燥用气相旋转换热器圆筒壁保温性能好坏的重要参数,对换热器内部换热环境及换热器整体的换热效率影响非常大。圆筒壁传热阻的大小不仅仅与自身材料性质、材料厚度及每层材料的密度等因素有关[2],也与材料所处的设备工作环境有关,包括换热器内部的风温、风速及外界环境温度等因素。圆筒壁的传热阻值越大,其保温性能越好,相应的对换热器换热效率的提升也越大[3]。由于粮食干燥用气相旋转换热器圆筒壁的传热阻测定时受到多种因素的影响[4-5],所以很难准确地标定出其材料的热工性能,经常会出现实际测量的热阻值与材料生产厂商提供的热阻值不同的情况。目前,常用于换热器圆筒壁结构传热阻的测量方法主要为接触式测量法,但存在操作复杂、测点孤立及测试环境要求高等问题[6]。随着近年来热像仪的发展进步,使用热像仪进行热成像故障诊断和检验测试成为了一种先进的手段而被广泛应用。相比于传统的接触式测量法,热成像法使用热像仪拍摄热谱图可以直观、无损进行测试[7],且操作简单、测试速度快,是一种十分便捷的传热阻测试方法。
本文将使用热成像法进行实验,运用热像仪对粮食干燥用气相旋转换热器圆筒壁进行热特性参数测定[8],与传统的接触式测量法进行对比,再结合理论计算数据对热成像法的测量结果进行评定[9],为换热器圆筒壁传热阻测量及保温性评定提供新的方法。
1 传热阻计算理论依据
1.1 热成像法传热阻计算
热像仪是一种通过热谱图拍摄准确、快速地测量物体表面温度的测量设备。在使用热像仪进行圆筒壁热工性能测试时,只能够测出圆筒壁表面的温度,实际测量计算时需要结合热平衡理论对换热器圆筒壁结构的传热阻进行一定的有效估算[10],以完成最后的计算要求。
使用热成像法进行传热阻计算时,需要将一维稳态导热条件下的导热微分方程与辐射换热和对流换热共同的边界条件相结合,并以此推导出使用热成像法测量圆筒壁传热阻R,计算公式为[11]
(1)
式中R—热成像法计算出的传热阻值(m2·K/W);
Tw—圆筒壁内表面温度(K);
Tref—圆筒壁反射温度(K);
Tin—换热器内部环境温度(K);
Tout—换热器外部环境温度(K);
hin—圆筒壁内壁表面对流换热系数(W/m2·K);
δ—斯蒂芬-玻尔兹曼常数,δ=5.67×10-8W/m2·K4。
由于旋转式换热器主要用于粮食烘干,而东北地区粮食烘干多在11月后进行,所以可将冬季换热器内壁的散热模型简化成壁面自然对流传热[12]。Churchill等人通过对大量的文献和数据的整理上推导出了自然对流传热的相关关联式,即
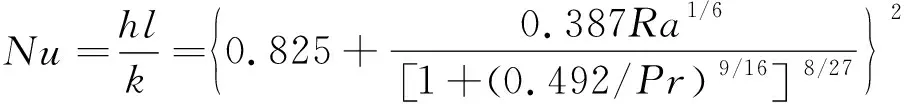
(2)
式中Nu—无量纲努塞尔数;
l—传热面的几何特征长度(m);
h—流体对流换热系数(W/m2·K);
k—静止流体的导热系数(W/m·℃);
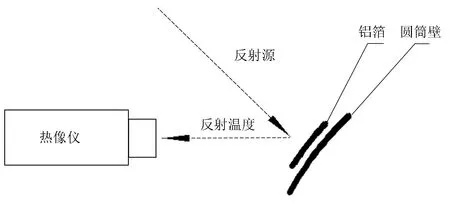
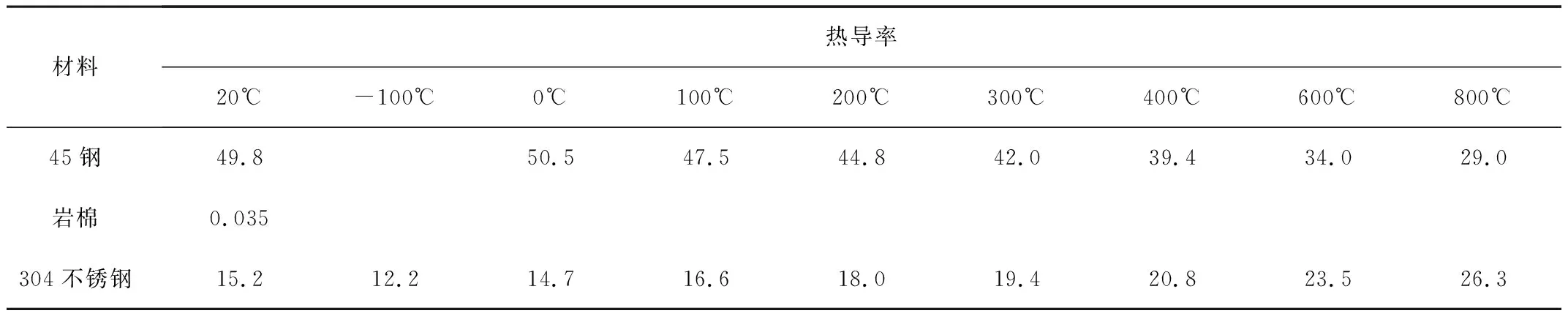
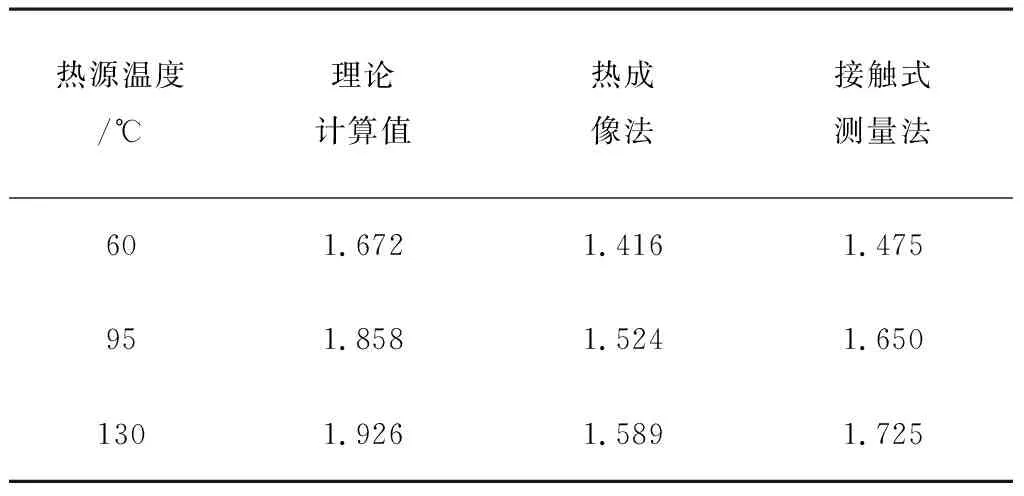
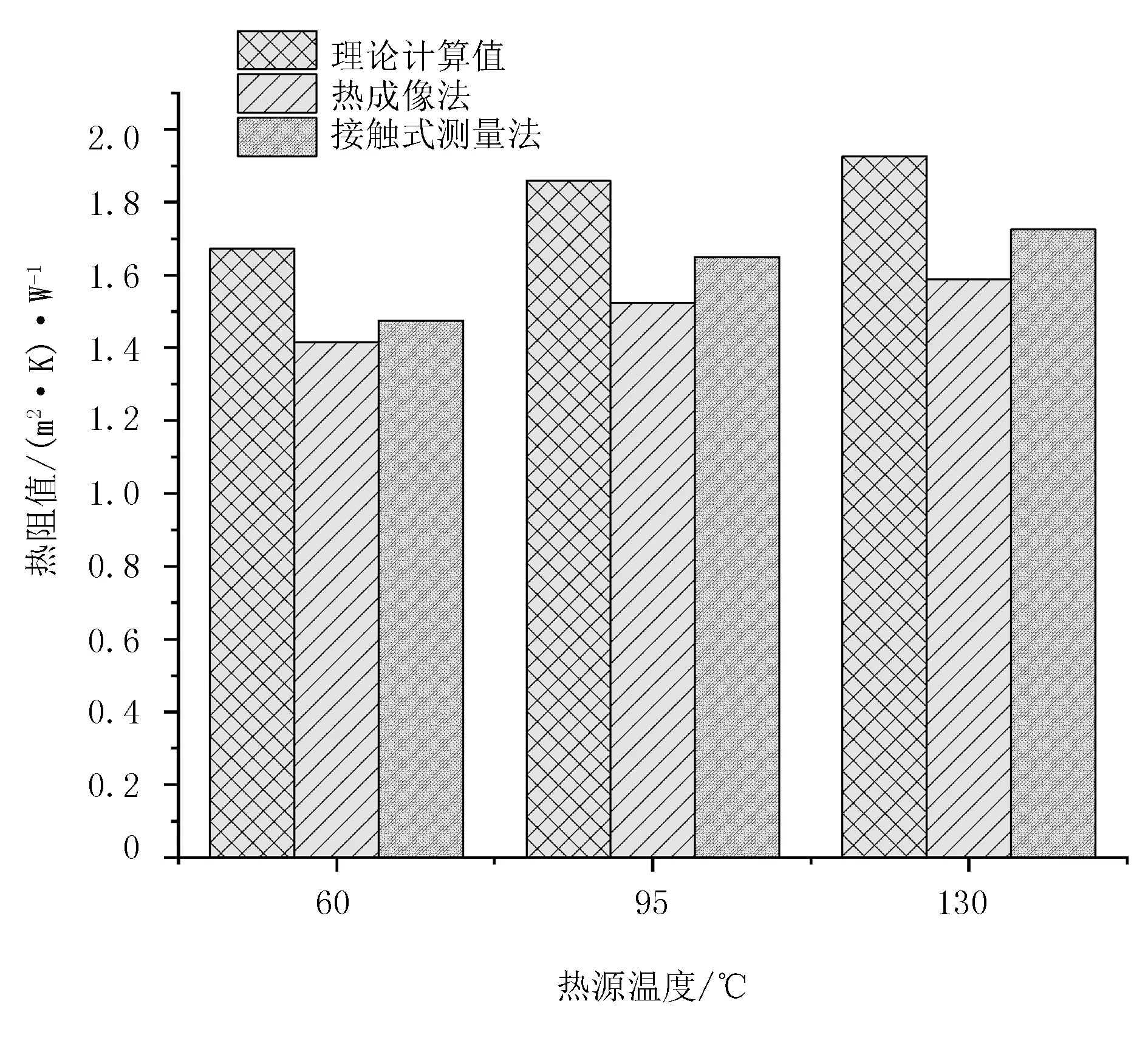
Ra—无量纲瑞利数,Ra取值范围为10-1 Pr—无量纲普朗特数;Pr取值范围为0 β—体积热膨胀系数(1/K); g—重力加速度(m/s2); θ—圆筒壁切线与竖直面夹角(°); α—热扩散率(m2/s); v—流体运动粘度(m2/s); Ts—竖直表面温度(K); Tf—特征温度(K),Tf=1/2(T∞+Ts); T∞—边界层外空气温度(K)。 公式使用限制条件为:表面温度Ts较为恒定,流体的流动形式为湍流或者层流形式。 将实验测试数据及相应的理论参数代入公式(2),即可计算出圆筒壁内表面的对流传换热系数hin。使用热成像法测圆筒壁表面温度情况时,也受到自身参数和外界环境的影响。在众多影响因素中,发射率ε和环境反射温度Tref对实验结果有较大影响。 1.1.1 圆筒壁表面发射率 粮食干燥用气相换热器的圆筒壁表面发射率ε不仅受材料本身性质影响,也与材料所处的环境温度湿度、材料的表面粗糙程度以及形状有关[13]。在实验中,可以根据热辐射基本原理进行计算。热像仪成像原理如图1所示。 图1 热像仪成像原理图Fig.1 Thermal imaging imaging schematic 图1中:ε为圆筒壁表面发射率;T为温度值;W为辐射能;τ为大气透射率;脚标obj、ref、atm则分别表示样本、反射以及空气环境。 在发射率计算过程中,首先将热像仪接收到的总辐射能确定出来,公式为 Wtot=ετWobj+(1-ε)τWref+(1-τ)Watm (3) 式中Wtot—热成像仪接收总辐射能(W/m2); Wobj—目标辐射能(W/m2); Wref—周围环境的反射辐射能(W/m2); Watm—大气辐射能(W/m2); ε—物体表面发射率; τ—大气透射率,由于换热器内大气透射率接近于1,所以计算中取τ=1。 化简上式得到圆筒壁表面的发射率计算公式为 (4) Wref=Eb1[Fb(0-λ2Tref)-Fb(0-λ1Tref)] Wobj=Eb2[Fb(0-λ2Tobj)-Fb(0-λ1Tobj)] 式中Eb1—温度为Tref时的黑体辐射力(W/m2); Eb2—温度为Tobj时的黑体辐射力(W/m2); λ1、λ2—波长(μm); Fb(0-λ2Tref)—温度为Tref时,波长在0~λ2范围内时黑体辐射力Eb1的百分数; Fb(0-λ1Tref)—温度为Tref时,波长在0~λ1范围内时黑体辐射力Eb1的百分数。 同理可知Fb(0-λ2Tobj)和Fb(0-λ1Tobj)。 由于实验所用的FLIR T420热像仪的辐射波长范围为8~14μm,所以在计算过程中λ1取值8μm,λ2取值14μm。 1.1.2 反射温度测量 在测量反射温度Tref时,由热像仪拍摄反射温度的原理可知:Tref可以看成是当将发射率约等于1的褶皱铝箔覆盖在圆筒壁表面时铝箔表面的温度[14]。测试方法如图2所示。 图2 测量圆筒壁表面反射温度原理图Fig.2 Measuring the reflection temperature of the cylinder wall surface 测试反射率的具体操作方法为:将褶皱的铝箔与圆筒壁同轴放置,调整热像仪的表面发射率,设置为1;将热像仪与被测试样保持一定距离,使热像图成像清晰,读取此时热像仪显示的铝箔表面温度,反复进行3次,取平均数,即为反射温度Tref。 在将热成像法应用于换热器圆筒壁传热阻测量之前,采用接触式测量法对圆筒壁进行传热阻测量。接触式测量法是以圆筒壁结构材料内外两侧对流及传热原理建立起热平衡,以此导出接触式测量法计算传热阻公式为 (7) 式中R2—接触式测量法测计算的传热阻; hin—圆筒壁内部换热系数; Tout、Tin、Tw在公式(1)中有交代。 选择黑龙江八一农垦大学智能装备实验室研发的粮食干燥用气相旋转换热器实验台为实验设备,如图3所示。 图3 气相旋转换热器实验台Fig.3 Gas phase rotary heat exchanger test bench 该实验台主要由壳程、管程及进出口等部件组成。其中,壳程主要为圆筒壁结构,是主要的保温元件之一,由45#钢、岩棉及304不锈钢组成。各组成部分的导热率如表1所示。 表1 圆筒壁组成材料及其热导率Table 1 Composition and thermal conductivity of cylinder wal 2.2.1 实验仪器 实验中热成像法测量圆筒壁传热阻方法测量外壁温度时,使用FLIR T420手持式热像仪,如图4所示。热像仪量程为-20~650℃,测量精度为±2%,波长范围7.5~14μm;传统的接触式测量法使用贴片式T型热电偶,其测量量程为-200°~350℃,测量精度为±5%,热电偶响应时间为3s,并使用与其配套的数采仪采集温度数据;圆筒壁内壁温度则采用换热器实验台安装的铂电阻温度传感器进行温度测量。 图4 Flir T420手持式红外热像仪Fig.4 Flir T420 hand-held infrared thermal imager 2.2.2 实验方法 热成像法测量圆筒壁传热阻在使用热像仪对圆筒壁外壁进行热谱图拍摄时,热像仪的视角为25°×19°,测量换热器整体高度为1.4 m,计算可得拍摄距离应为4m。根据换热器圆筒壁长度,选取2个点对换热器外壁进行拍摄,每个拍摄点拍摄3次,换热器拍摄点布置图如图5所示。 实验进行时,设置换热器热源温度分别为130℃、95℃、60℃,并分别在每组温度下进行3次实验,旋转换热器圆筒壁外壁温度由热成像法和T热电偶同时测量热谱图如图6所示。内壁温度则使用换热器实验台自带的铂电阻温度传感器测量,设置换热器控制柜对内部温度的数据采集时间间隔为每1min记录1次。 图6 圆筒壁外壁热谱图Fig.6 Heat spectrum of outer wall of cylinder wall 在分析热像仪所拍摄的热谱图时,利用MatLab软件对热谱图进行分析,并采集其中有效的温度数据,然后于热电偶数采仪及换热器控制柜中提取所需的外表面温度和内表面温度,再利用Origin软件对以上数据进行处理与分析。 分析时,将热成像法、接触式测量法与理论计算法结果进行比对。其中,热成像法和接触式测量法的计算用之前所述公式计算求得。圆筒壁稳态导热传热阻理论计算公式为[15]。 (8) 式中Rλ—理论计算传热阻值(m2·K/W); tw1、tw4—圆筒壁内、外壁温度值(℃); r—圆筒壁半径(m); l—圆筒壁长度(m); q—热流密度(J/m2·s)。 运用上述公式计算出理论热阻值,再利用公式(1)和公式(7)分别计算出热成像法热阻值及接触式测量法热阻值,结果如表2所示。 表2 不同温度条件和不同测量方法下的圆筒壁传热阻值Table 2 The heat transfer resistance of the cylinder wall under different measuring methods under different temperature conditions m2·K/W 由表2可知:使用热成像法和接触式测量法测量计算出的圆筒壁传热阻值均小于理论计算。原因如下:换热器在日常使用过程中,随着圆筒壁材料的老化、磨损、腐蚀等因素的影响,会使圆筒壁的实际热阻值比设计热阻值有所降低,且实验误差也是造成以上现象出现的原因之一。 为了进一步比较热成像法与接触式测量法的可靠性,将3种结果绘制成柱形图(见图7),并通过偏差的百分比对不同的测试方法进行比较。 图7 测试值与理论计算值柱状图Fig.7 Histogram of test and theoretical values 由图7可知:两种方法测量计算所得的传热阻值与理论计算值均存在一定的偏差:热成像法测得的传热阻值与理论计算值偏差在15%~20%之间,接触式测量法偏差小于15%,相比之下接触式测量法偏差较小。由于两种测量方法偏差值均小于20%,因此结果均比较可靠。 1)由于受到圆筒壁材料老化、磨损、腐蚀等影响,热成像法和接触式测量法测得的传热阻值均小于理论计算的圆筒壁传热阻值。 2)对比两种方法可知:接触式测量法与理论计算值偏差小于15%,热成像法传热阻值与理论计算值偏差在15%~20%之间,利用接触式测量法计算得到的阻值与理论计算值吻合度更高。 3)相比接触式测量法,热成像法的测量计算原理融入了圆筒壁结构的辐射传热过程,理论基础完善。综合考虑到环境因素对换热器圆筒壁传热阻测量的影响,热成像法的操作更为便利。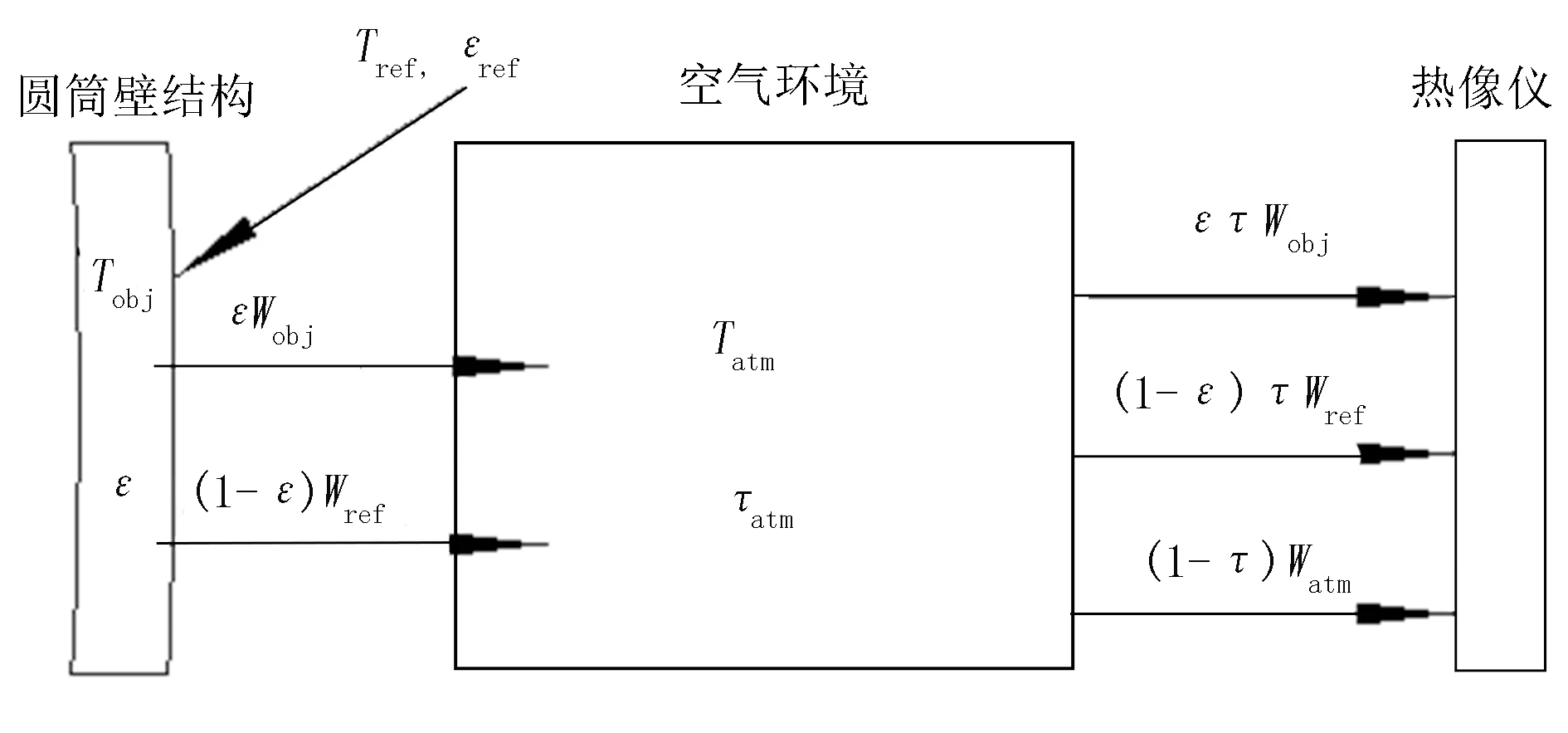
1.2 其他传热阻测量方法
2 实验设备与方法
2.1 实验对象

2.2 实验仪器及实验方法

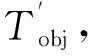

2.3 数据处理
3 结果与分析
3.1 热阻值的理论计算值与测试值
3.2 测试值与理论计算值吻合度
4 结论

