超大直径空心独立复合桩的竖向承载力计算方法

2

(1.长安大学 公路学院，西安 710064；2.陇东学院 土木工程学院，甘肃 庆阳 745000；3.安徽建工集团有限公司，合肥 230000)

1 研究背景

随着我国岩土工程的迅速发展，对桩基承载力的要求越来越高，导致桩基础直径、埋深越来越大[1-4]。大直径空心桩是20世纪90年代初期应用于我国的一种新型深基础形式，该桩型优点突出。关于大直径空心桩的承载特性，冯忠居等[5-9]从理论计算、模型试验、数值仿真等不同方面对其进行了研究，为该桩型在工程中的推广应用奠定了理论基础。

近年来，在大直径空心桩的基础上，国内发展出一种新型桩基础结构形式——超大直径空心独立复合桩，该桩型不仅延续大直径空心桩的优点，同时由于空心桩桩周注浆土体的存在，使桩土间相互作用增强，大大提高了桩周摩阻力，且外围的水泥搅拌桩为施工期的成孔安全提供了有力保障。然而，目前对超大直径空心独立复合桩基础的承载特性研究匮乏，特别是对于该新型桩的承载力计算方法，国内外尚未见报道。研究超大直径空心独立复合桩的承载力计算方法对推进我国大直径空心桩的发展具有重要意义。

基于此，本文根据超大直径空心独立复合桩的受力特点，考虑桩的径向非均匀介质分布，引入等效弹性模量的概念，基于双曲线模型下的荷载传递法，提出超大直径空心独立复合桩的承载力计算方法，并在此基础上提出了能综合反映桩身尺寸影响的复合桩竖向极限承载力公式，可为今后类似工程提供一定理论参考。

2 理论计算

2.1 等效弹性模量的引入

由于超大直径空心独立复合桩属于径向非均质材料，在受力方面较普通的均质大直径桩更为复杂。本文引入等效弹性模量这一概念将非均质的弹性模量等效为均质的弹性模量，以此为基础计算出超大直径空心独立复合桩的竖向极限承载力，将显著降低计算的复杂性。

本研究中假定在桩顶竖向荷载作用下将引起大直径桩、注浆土、水泥搅拌桩三相产生相同的应变，建立的等效弹性模型为

E=φ1E1+φ2E2+φ3E3。

(1)

式中：E为复合材料的等效弹性模量；E1为复合材料中相1的弹性模量；E2为复合材料中相2的弹性模量；E3为复合材料中相3的弹性模量；φ1，φ2，φ3分别为复合材料中相1、相2、相3的体积分数，且φ1+φ2+φ3=1。以下理论公式中的E为等效弹性模量，D为超大直径空心独立复合桩的桩径，研究图示中的桩都为复合桩体。

2.2 荷载传递模型的建立

荷载传递法就是将桩划分为许多弹性单元，每一个单元与土体之间通过非线性弹簧相互联系，以模拟桩与土之间的荷载传递关系。本文的桩侧阻力和桩端阻力与桩身沉降之间的关系都将采用双曲线模型进行描述，如图1所示。此双曲线荷载传递函数表示为

(2)

式中：τ为单位长度的桩侧摩阻力或者桩端阻力；S为桩身位移；a和b为荷载传递参数。

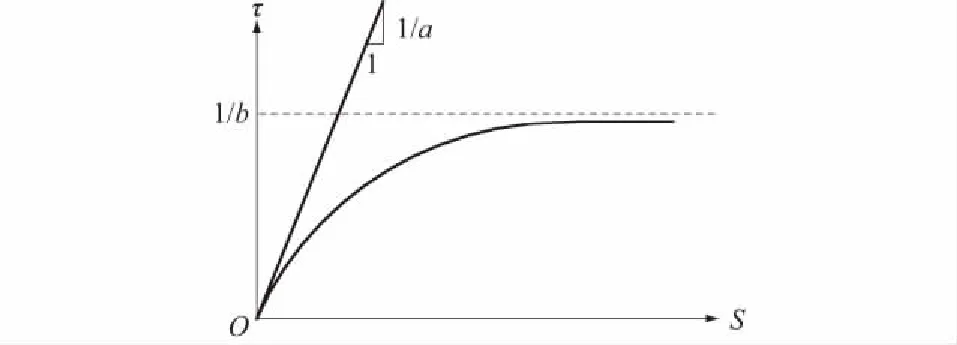
图1 桩侧阻力或桩端阻力与桩身位移的关系

2.3 桩身荷载传递微分方程的建立及求解

2.3.1 微分方程的建立

桩基础在竖向荷载作用下，桩与土相互作用的模型如图2所示。

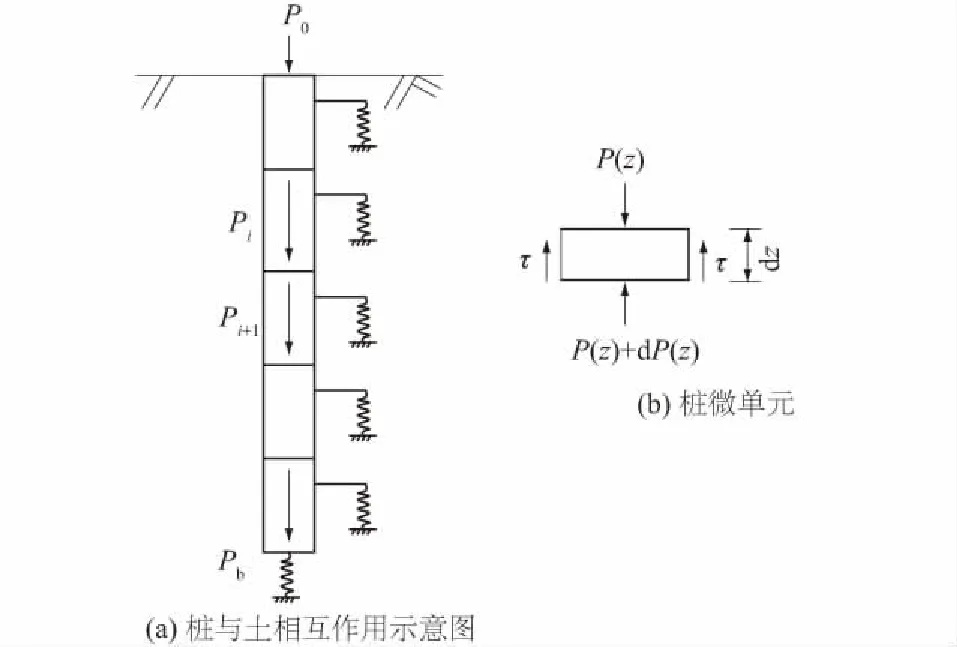
图2 桩与土相互作用的模型

取桩身上任意一个微单元，根据静力平衡条件可得

(3)

式中：P为桩身荷载；up为桩身周长；z为桩身入土深度。

根据应变的定义可以得到任意微单元体产生的弹性压缩量为

(4)

式中A为桩身横截面面积。

由于

(5)

可以得到

(6)

将荷载传递双曲线模型关系式(2)代入式(6)可以得到桩身荷载传递的微分方程，即

(7)

2.3.2 微分方程的求解

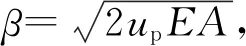
(8)

式中β为与桩身截面周长、桩身截面面积、桩身弹性模量有关的常数。

由于此微分方程只考虑了桩的初始条件而未考虑桩的边界条件，故式(8)只反映了桩身任意截面处的弹性压缩量与其对应的轴力之间的关系，而不包含桩端土沉降变形对于桩身轴力的影响。然而桩顶的总沉降变形量S0包括桩身的压缩变形量Se(z)和桩端土的沉降变形量Sb两部分[10]，故根据荷载传递双曲线模型引入桩端土的沉降变形量与其对应的桩端阻力Pb之间的关系式，即

(9)

式中：Pb为桩端轴力；σb为桩端应力；Sb为桩端土沉降变形量；ab和bb为桩端地基荷载传递参数。

令桩身任意截面处的荷载为P(z)，由使桩身产生弹性压缩量所需的轴力Pe(z)和使桩端土产生沉降变形量所需的轴力Pb构成，并将式(8)和式(9)代入即可得到其表达式为

P(z)=Pe(z)+Pb=

(10)

式中as和bs为桩侧土层荷载传递参数。

当在桩顶处z=0时，Se(0)=Se0，此处的Se0为整个桩身产生的总的弹性压缩量，因此可以得到桩的P-S曲线表达式，即

(11)

当桩穿过不同性质的土层时，可将其荷载沉降关系表达为

(12)

式中：n为桩所穿过的不同性质的土层的层数；asi和bsi为与桩侧第i层土的性质有关的荷载传递参数。

2.4 公式应用

本文引用安徽省江淮地区地质勘察资料，应用理论公式，绘制出桩顶的P0-S0曲线，从而计算出超大直径空心独立复合桩的极限承载力。其中，土层从上到下分布有粉土、粉质黏土、黏土、细砂、全风化泥质砂岩、强风化泥质砂岩、中风化泥质砂岩等，但由于桩主要穿越粉土层和粉质黏土层，故在计算中以粉土作为上层土，以粉质黏土作为持力层土，桩端在持力层下的深度为4 m。具体桩土参数见表1，不同土层中摩阻力及轴力沿桩身的分布如图3所示。此外，桩侧注浆土的环壁厚度为0.5 m，水泥搅拌桩环壁厚度为0.55 m，桩径和桩长将随着工况进行变化，总工况包括25种(内部空心桩桩径分为2.5，3.5，5.0，7.5，10.0 m 5种情况；桩长分为10，20，30，40，50 m 5种情况)。

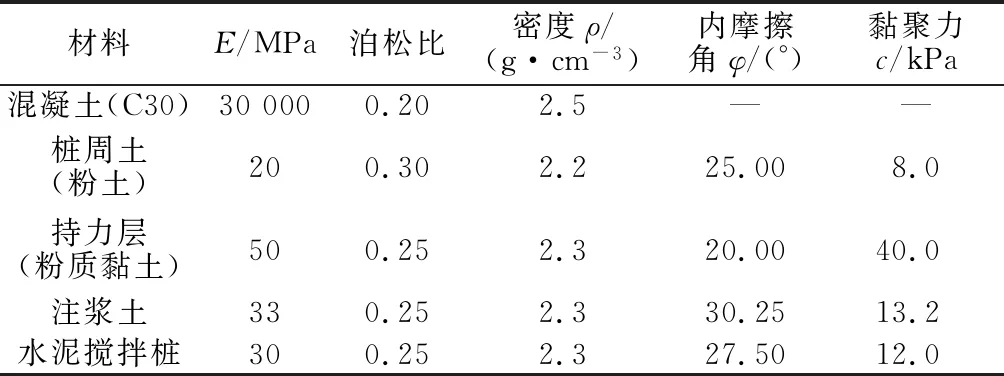
表1 安徽省江淮地区桩土力学参数

注：a1、b1、a2、b2分别为第1层和第2层土的荷载传递参数；l1为桩在土层1中的长度；l2为桩在土层2中的长度；Sb为桩端位移；τ0为桩顶截面处的桩侧摩阻力；τ1为a截面处位于土层1的桩侧摩阻力；τ2为a截面处位于土层2的桩侧摩阻力；τb为桩端截面处的桩侧摩阻力；Pe1为位于土层1中的桩侧阻力；Pe2为位于土层2中的桩侧阻力。图3 不同土层中摩阻力及轴力沿桩身的分布

由上述公式可知

(13)

大量实测资料表明：同一土层桩身轴力可近似按直线分布。因此，曲线段1—2和曲线段2—3(图3)可近似由直线段来代替。所得a截面处的桩身轴力为

P′a=Pb+upl2τb。

(14)

则a—b段按弹性Hooke定律计算得到的桩身弹性压缩量为

(15)

式中E为超大直径空心独立复合桩的等效弹性模量。代入式(8)可得相应的弹性轴力为

由图3可知，a截面处的桩身轴力Pa和沉降Sa分别为：

Pa=Pb+Pea；

(17)

Sa=Sb+Sea。

(18)

在a截面处上、下侧的桩侧摩阻力分别为：

(19)

则可得到桩顶轴力近似值为

(20)

同理可得0—a段桩身弹性压缩量为：

(21)

Se0=Sea+Se0a。

(22)

再次代入式(8)可得：

(23)

P0=Pa+Pe0=Pb+Pea+Pe0；

(24)

S0=Sb+Se0=Sb+Sea+Se0a。

(25)

令Sb为不同数值即可计算得到不同的P0和S0，由此可绘制出桩顶的P0-S0曲线，从而计算出超大直径空心独立复合桩的极限承载力。

理论计算将采用上述计算公式，并利用MatLab软件进行编程计算，得到理论上不同桩长、桩径下的竖向极限承载力，如图4所示。

图4 理论计算的不同桩长、桩径下的竖向极限承载力

3 数值计算

3.1 模型建立

本文采用Marc有限元软件建立数值模型，在建立模型过程中，具体工况、几何尺寸及桩土参数和上述公式应用取值一致，超大直径空心独立复合桩的几何模型如图5所示。

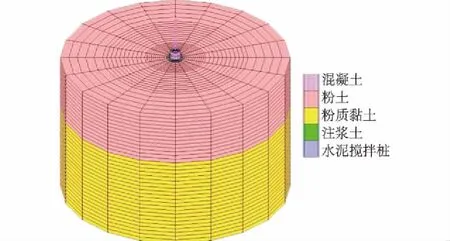
图5 几何模型(以桩径5 m，桩长30 m为例)

3.2 竖向极限承载力

取桩顶沉降量为40 mm[11]时对应的桩顶荷载作为超大直径空心独立复合桩的竖向极限承载力，根据数值模拟得到不同桩径、桩长下的竖向极限承载力，如图6所示。

图6 数值模拟的不同桩径、桩长下的竖向极限承载力

从图6可知，随着桩长、桩径的增加，超大直径空心独立复合桩的竖向极限承载力大幅提高。由于数值模型的建立存在一定的操作复杂性，为了能够更加高效简便地计算出超大直径空心独立复合桩的竖向极限承载力，下面将进行理论计算与数值计算的对比与改进，以期提出考虑桩身尺寸影响的更为合理的超大直径空心独立复合桩的承载力计算公式。

4 理论计算与数值计算的对比与改进

为了探讨理论计算与数值计算的差别，以下将进行数值计算并与理论计算进行对比分析。

将图4与图6对比分析可知，当桩径D<5 m时，超大直径空心独立复合桩的竖向极限承载力理论计算值与数值计算值的差别较小，最大差值1.54 MN；当桩径D≥5 m时，超大直径空心独立复合桩的竖向极限承载力理论计算值与数值计算值的差别较大，最大差值甚至达到了17.27 MN。

究其原因，在公式应用中为简化计算，在每层土中分别采用了最小桩侧摩阻力τb和τ1作为计算值。由式(14)和式(20)可知，当桩侧摩阻力偏小时，随着桩径和桩长增大，计算得到的相应位移下的轴力越小。因此采用理论计算得到的极限承载力在桩径和桩长较小时与数值模拟计算结果接近，而当桩径和桩长超出一定范围后，理论计算值将明显小于数值计算值。

考虑到超大直径空心独立复合桩的竖向极限承载力的大小受桩径和桩长的影响，故当桩径D≥5 m时，引入综合考虑桩径和桩长的影响因子DL，经过多次试算与验证，确定其大小为(D-5)+(D/3)·[(L-10)/10]，最终确定超大直径空心独立复合桩的竖向极限承载力理论公式为

改进后的理论公式计算值与数值计算值基本吻合。由此可知，新建的理论公式弥补了原有桩径、桩长因素对其极限承载力计算的影响，适用于更大桩径、桩长下的超大直径空心独立复合桩的竖向极限承载力计算。

5 结 论

(1)根据超大直径空心独立复合桩的受力特点，考虑桩的径向非均匀介质分布，引入等效弹性模量的概念，基于双曲线模型下的荷载传递法，提出了超大直径空心独立复合桩的承载力计算方法。

(2)以安徽省江淮地区典型地质条件为依据，建立了超大直径空心独立复合桩的数值模型，得到了不同桩径、桩长下的竖向极限承载力。

(3)分析公式应用中的简化条件并找到了理论计算与数值计算产生偏差的原因，由此引入综合考虑桩径和桩长的影响因子，提出了更为合理的超大直径空心独立复合桩的竖向极限承载力计算方法。