工件图像轮廓角点特征提取算法

刘 晨， 于微波， 杨宏韬， 王国秀， 谢家欣

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)

0 引 言

随着工厂机械化程度的提高，机器视觉测量技术因具有非接触、精度高、速度快的优点，被各种领域广泛应用，比如工件尺寸检测等。在工件尺寸检测中，特征提取是重要环节，用以提高获取工件图像的质量,便于计算机对其分析、识别。在对采集的工件图像进行预处理之后，为了能够精确地对其进行尺寸测量，需要对图像的一些特征进行提取，如角、点、线等。在进行特征提取时采用的算法也会影响尺寸的测量精度，因此对工件特征提取算法的研究十分有意义。

将获取的目标图像与背景之间的闭合曲线称为图像的轮廓。而轮廓提取则是将上述闭合曲线提取出来,并以较为明显的方式显示出来[1]。

经典的轮廓检测方法是先利用传统的边缘检测算子检测出目标图像的粗边缘，再将多余的伪边缘去除,达到细化边缘的目的。缺点则是运行时间过长且精度不高，不适合应用于工厂实时在线检测。随着研究的深入，现阶段出现了很多轮廓提取算法。其中，梯度法、形态学轮廓算法以及水平集算法[2],虽然去除了冗余的轮廓，减小了数据处理量，能较为准确的将目标轮廓提取，但是容易被噪声干扰，而且应用领域范围太小，导致最终效果不理想。在现阶段的活动轮廓法中应用较广的则是Snake模型法[3]。该算法结合了图像数据、轮廓估计、模型收敛等方法，轮廓提取效果良好，缺点则是初始轮廓敏感，会影响最终的提取效果。因此，提出一种基于角点特征的工件图像轮廓提取算法，利用Harris算子进行Snake轮廓初始位置的设置，然后对图像进行轮廓提取。

1 Harris角点检测算法

将图像中灰度变化剧烈或者在图像边界上曲率变化较大的点称为角点[4]。角点检测对于工件图像的特征点定位有着重要作用，在进行工件的特征提取时,角点检测能够精确定位特征点，提高工件图像的特征提取精度[5-8]。

在进行角点检测过程中，可能会受到噪声干扰以及图像灰度变化的影响,从而导致角点检测结果不准确。而Harris角点检测算法不仅可以有效地克服这些问题，而且计算量较少，实现简单，使得检测结果更加准确。

在Harris算法检测过程中，将图像I(x,y)在点(u,v)平移(x,y)产生的灰度变化函数表示为

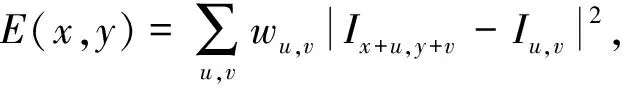
(1)

式中：w----高斯函数。

函数E(x,y)值在高斯窗口内进行任意方向的移动时，若未产生任何变化或者有微小变化,则为非角点；当函数E(x,y)产生特别大或者特别小的变化时，则将该点定义为角点。

在点(u,v)处对函数E(x,y)进行一阶泰勒展开，则函数E(x,y)可改写成下式

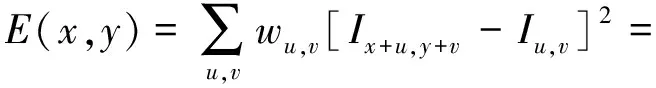
Ax2+By2+2Cxy，

(2)

其中，A，B，C是二阶方向微分的近似，定义如下

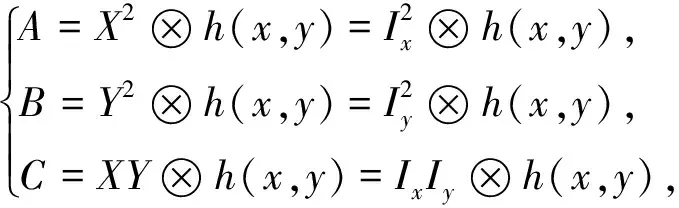
(3)

其中，X，Y分别表示在x和y两个方向上的一阶梯度值：

式中：h(x,y)----高斯滤波。

将式(3)代入式(2)，可得到下式

(4)

其中，M为自相关矩阵，表示如下

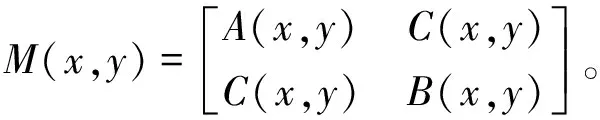
(5)

计算自相关矩阵M特征值过程过于繁复，所以Harris算法使用角点响应函数进行角点质量判断，如

R(x,y)=Det(M)-kTr(M)2，

(6)

式中：Det(M)----矩阵M行列式的值，Det(M)=AB-C2；

k----常数系数；

Tr(M)----矩阵M的迹，Tr(M)=A+B。

若提前设置的阈值小于等于某点的R(x,y)值，该点则为角点。

Harris角点检测流程如图1所示。

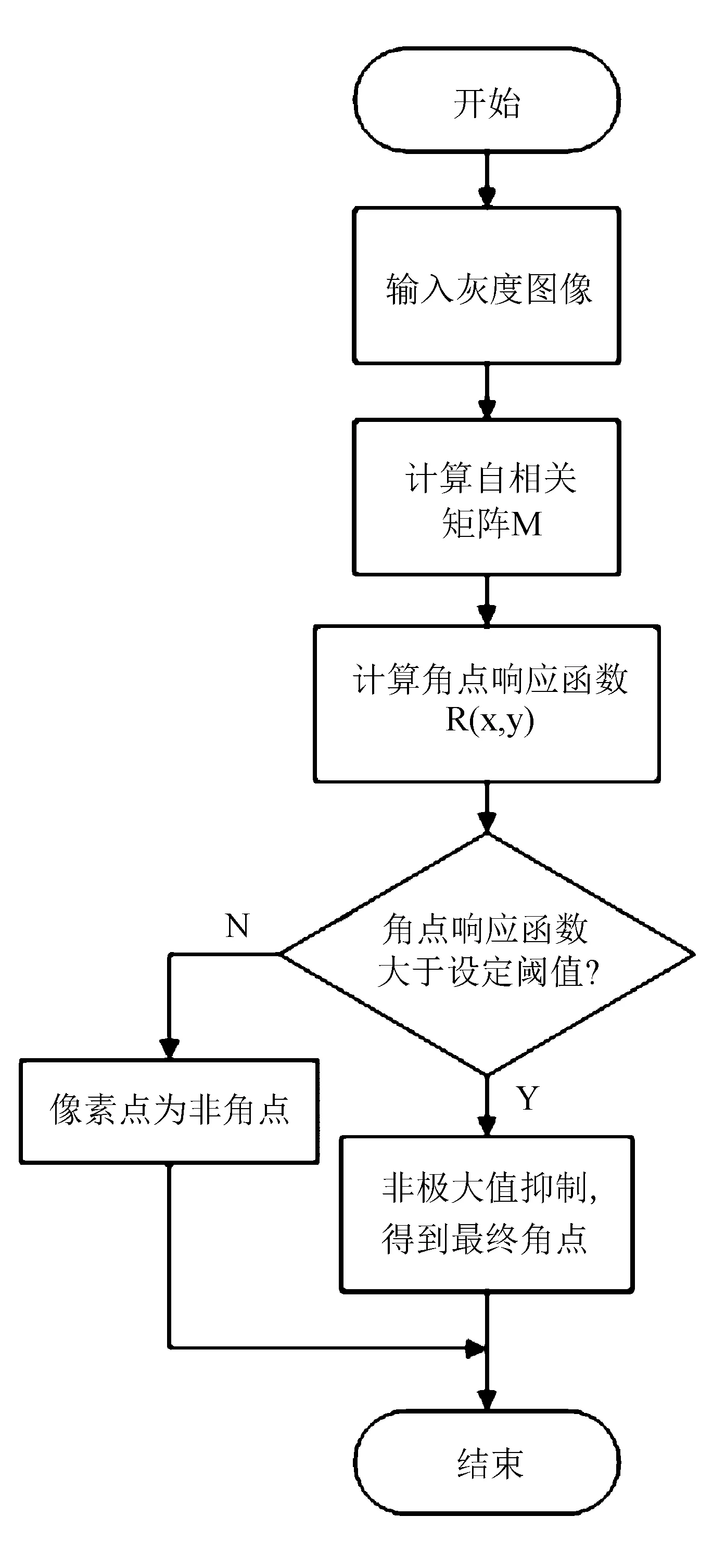
图1 Harris角点检测流程图

算法具体步骤如下：

1)获取齿轮工件原图的灰度图像，计算其在x和y方向上的梯度值X和Y；

2)用高斯函数对工件灰度图进行滤波处理，并计算出自相关矩阵M；

3)将设定的阈值与计算得到的每个像素点的响应值进行比较，并判定该点是否为候选角点；

4)利用非极大值抑制对3)中所获得的候选角点进行处理，以确定最终的角点。

2 基于Snake模型轮廓提取算法

2.1 图像分割

在提取轮廓特征之前需要对图像进行分割，能够更精确地提取工件图像的轮廓特征。图像分割算法的目的是将对象与背景分离，其步骤如下：

1)对整个图像进行搜索,并对目标对象和背景进行标记；

2)将标记的目标和背景进行区域分组；

3)将图像中的目标与背景分离[9]。

在众多图像分割算法中，阈值分割算法因其计算量少、实现简单以及性能稳定等优点被广泛应用，所以最终选择阈值分割算法进行实验。而现阶段在阈值分割法中，OTSU法(又叫大津法)是应用最广泛的分割算法。

大津法能够进行自适应阈值分割，其原理是利用阈值将原图像分成背景区域和目标工件区域两个部分，然后计算该最大类间方差的最佳阈值以使得两区域的区别度最大。设大小为M×N的图像在像素点(x,y)的灰度值为f(x,y)，灰度取值范围为[0,L-1]，可记为HL=[0,1,2,…,L-1](L为灰度级)。设f(x,y)中灰度级为i出现的概率为

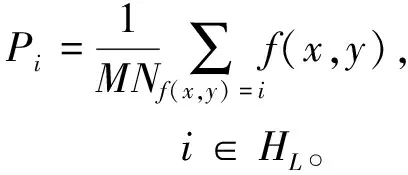
(7)

将获取的图像分为目标工件区域A和背景区域B，若原来设置的分割阈值为T,则区域A的灰度级范围为[0,T]，区域B的灰度级范围为[T+1,L-1]，那么区域A和区域B的概率分别如下：

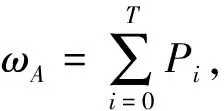
(8)

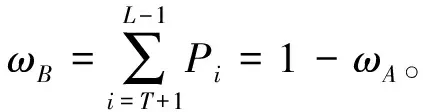
(9)

这两区域各自对应的灰度均值分别为：

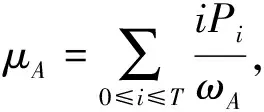
(10)

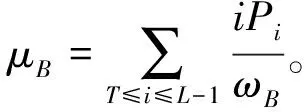
(11)

计算工件图像整体均值

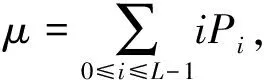
(12)

然后计算目标工件区域A和背景区域B的类间方差

σ2=ωA(μA-μ)2+ωB(μB-μ)2。

(13)

通过下式可知，当σ2最大时为最佳阈值。该方法计算量较小且能够自动确定最佳阈值，可准确地分割目标工件和背景区域。

T=maxσ2=

max|ωA(μA-μ)2+ωB(μB-μ)2|。

(14)

2.2 轮廓提取

Snake模型轮廓提取算法最重要的一步是利用在原始图像的封闭曲线最小能量函数表示工件图像的轮廓。设原始图像中闭合轮廓曲线为

V(s)=(x(s),y(s))，

其中，s∈[0,1]为轮廓曲线的弧长，通过找到一条连续闭合曲线使得Esnake最小,

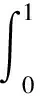
(15)

外部能量计算方法为

Eext(V(s))=Eimage(V(s))+Econ(V(s)),

(16)

其中，Eimage(V(s))表示的图像能量力能够保证寻找的曲线接近物体真实轮廓。Econ(V(s))代表的控制力是外部作用力，由人为施加。它能使曲线更准确地收敛到真实边界。

共建是社会治理系统的建构基础，也是社会治理系统功能发挥的基本前提。在共建共治共享社会治理格局的系统构建中，如果说共建是系统治理的基础，那么共治就是实现系统治理的手段，而共享就是系统治理的目的。在复杂条件下实现政府治理与其他多元主体的合作共建，在理念创新上体现国家治理、政府治理和社会治理模式的转变，而这种转变就是以系统建构的方式体现在多元主体的社会共识之中，具体化在多元主体合作共建的过程之中。为此需要从以下三个方面作出努力。

内部能量计算方法为

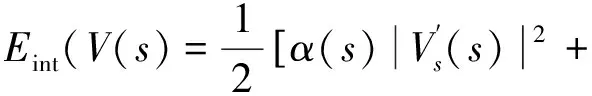
β(s)|Vs′′(s)|2]，

(17)

利用Harris算子与Snake模型相结合进行轮廓提取的具体流程如图2所示。

图2 基于Harris算子的Snake模型的轮廓提取流程

3 实验结果及分析

为了验证基于角点特征的工件图像轮廓提取算法能更好地提取工件图像的轮廓，文中以齿轮工件为对象进行实验研究。

3.1 Harris角点检测实验

为了验证Harris角点检测算法能更好地对Snake轮廓的初始位置进行设置，文中选用Harris算子和SUSAN算子分别对齿轮图像进行角点检测，以角点错检率δ1和角点漏检率δ2作为衡量标准。

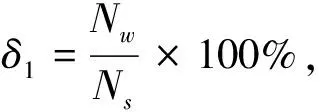
(18)

(19)

式中：Nw----错检测的角点个数；

Ns----检测的角点总个数；

Nl----漏检测的角点个数；

Nt----图像实际检测角点个数。

角点检测结果和检测情况分别如图3和表1所示。

(a) SUSAN算子

(b) Harris算子

表1 角点检测情况

通过实验可以看出，Harris算子可以将所需所有角点准确检测出来，且几乎没有伪角点与漏检角点,错检率为4.22%，漏检率为2.81%。SUSAN算子在检测角点时，只检测出一部分所需角点，漏检角点与伪角点较多,错检率为13.27%，漏检率为14.29%。这表明Harris算法能准确提取齿轮工件图像的角点，更好地对Snake轮廓的初始位置进行设置。

3.2 基于Harris算子的Snake轮廓提取实验

在进行轮廓提取之前，先采用OTSU阈值分割算法对齿轮工件进行图像分割。阈值分割效果如图4所示。

图4 OTSU阈值分割

之后，再对图像分割后的齿轮工件图像进行轮廓特征提取实验。

1)输入Harris算子检测出角点坐标；

2)利用样条插值对Snake初始位置进行设置，如图5所示。

图5 Harris算子对Snake轮廓初始位置的设置

3)填充封闭的Snake边缘区域，并将图像轮廓提取，实验效果如图6所示。

图6 提取齿轮工件轮廓图

从图5和图6中可以看出，Harris对Snake轮廓初始位置的设置更为准确，最终提取到的齿轮工件的轮廓更连续、精确。

4 结 语

轮廓提取的精确性对工件尺寸测量的准确至关重要，文中提出了基于角点特征的工件图像轮廓提取算法，并进行了实验验证。首先，利用Harris算子对Snake初始位置进行了较为准确的设置；然后用高斯滤波对获取的图像进行去噪处理，并计算得到Snake轮廓的内、外部能量；再以迭代的方法计算出Esnake的最小值，细化图像轮廓外缘。最后填充封闭的Snake边缘区域，得到准确的工件轮廓。实验结果表明，算法能更好地提取工件轮廓，提高了工件图像特征提取的准确性。