梯级水电站群高水头巨型机组不规则多限制区自动规避方法

程春田，赵志鹏，靳晓雨，刘令军，钟儒鸿

（大连理工大学，辽宁 大连 116024）

1 研究背景

最近二十多年以来，我国在西南集中建成了以金沙江、澜沧江、雅砻江、乌江、大渡河、红水河等干流梯级水电站群为代表的巨型梯级水电站群，高水头、大容量、巨型机组、远距离、跨省跨区域输送是其不同于以往中小流域的根本特征。由于高压瞬变流，这些干流梯级巨型水电站普遍存在多个不规则机组限制区。当水电站或机组响应单个甚至多个受端电网负荷需求及水电电力市场化后时段出力波动频繁时，由于水电站时段间和梯级上下游间紧密的水力联系，容易引起水电站自身后续时段和梯级上下游水电站群出力、水头和流量发生级联变化，从而给水电站和梯级水电站群运行带来巨大困难，严重影响水电站和电网安全经济运行，成为制约西南水电安全经济运行的技术瓶颈。

事实上，水电机组限制区问题一直是国内外水电机组组合（Hydro Unit Commitment，HUC）的经典问题，以往大多数研究主要集中在规则限制区建模与求解。Guan等[1]利用拉格朗日松弛法对规则限制区约束进行处理，将梯级水电调度问题转化为一个由动态规划和网络流算法解决的双层优化问题，取得了良好的结果。Bo等[2]、Borghetti等[3]和 Diniz等[4]均采用混合整数线性规划（MILP）方法对规则限制区进行建模，对梯级水电机组组合问题进行了求解。随着我国西南地区巨型梯级水电站群陆续建成，巨型机组高水头不规则多限制区问题已经成为电网、发电企业面临的棘手问题，基于工程中发现的问题，程春田等[5-6]提出了将机组不规则限制区通过组合数学的方式转化成电站的限制区，通过厂站组合和启发式策略规避机组限制区问题，但对于变化频繁、要求更高的机组组合问题，上述方法还是略显不足，需要更高效的多个高水头不规则限制区快速自动规避方法。对于有复杂不规则机组限制区的HUC问题，国际上普遍采用MILP对问题进行建模求解[7-8]。MILP方法因为相对成熟的数学理论和良好的全局搜索能力、灵活的建模方式及有大量成熟的开源和商业求解器可以调用，是求解HUC问题最常用的数学规划方法之一。Li等[7]采用基于人工剖分的方式对三峡电站存在的限制区进行MILP建模，实现了对32台机组组合的高效求解，但该方法依赖特定电站的限制区特征和人工经验，不适合自动化优化建模。Cheng等[8]提出一种基于分段线性化的不规则限制区MILP建模方法，实现了对乌江流域构皮滩单个电站的不规则限制区的建模与求解。但是其限制区边界描述需要事先由人工确定，对限制区数据形式有一定要求，难以实现模型的自动化建模及应用。

为解决机组多不规则限制区快速规避和自动建模问题，本文以水电系统运行中常见的调峰需求为目标，提出基于Hertel-Mehlhorn凸剖分算法的多个不规则限制区约束自动解析技术、并应用凸优化理论及析取规划理论方法构建复杂不规则限制区约束的MILP模型，然后应用商用求解器对问题求解，从而实现了复杂水电系统调度运行自动建模和问题求解。提出的方法在西南某干流流域梯级水电站群进行了方法验证，下面将详细介绍方法原理和具体的验证情况。

2 高水头巨型机组多个不规则限制区问题及其约束自动建模处理

据统计，世界上坝高200 m以上的水电站70%在中国，单机容量达到或者超过700 MW的水轮机组大多在中国，这样就产生了非常独特的西南地区高水头巨型机组多个不规则限制区问题。不同于以往中低水头和中下容量的机组规则限制区情况（图1（a）），高水头巨型机组多个不规则限制区边界条件复杂（图1（b）（c）），不能在工程应用通过简单设定固定的出力条件就可快速解决此问题，这个问题随着水电站或者机组对频繁变化的负荷需求的响应而愈加困难，因此成为西南地区水电系统运行的瓶颈问题。为了自动识别和避开复杂的机组限制区，我们在此提出机组限制区约束的通用数学表达。

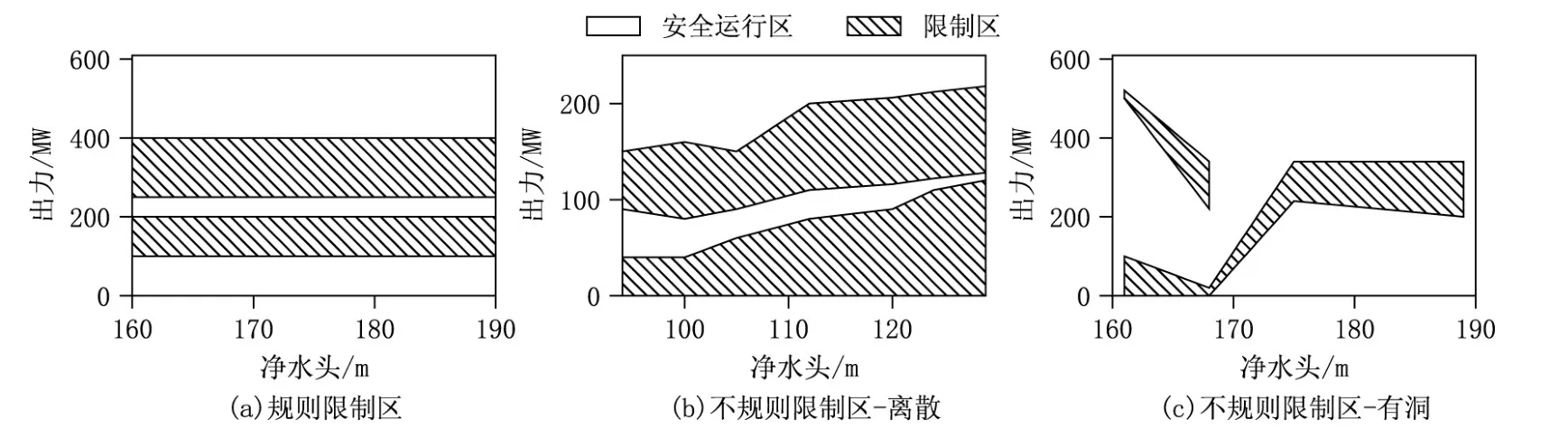
图1 限制区示意图

2.1 机组限制区约束的数学化定义首先，假设各限制区外边界均为简单多边形，即任何不相邻边不相交。该假设符合目前已知的水电机组限制区特征。在实际工程中，可以直接获取的数据包括：限制区边界点，机组出力上下限，机组净水头上下限等。根据这些数据，进行如下定义：

式中：Rm表示机组第m个子限制区，R表示机组的限制区组合，Poly()表示由括号内点集依次相连，首尾相接组成的有界多边形平面区域。(Hm，j，Pm，j)表示机组第m个限制区上的第j点。 M 表示机组含有的子限制区个数，Jm表示机组限制区m所包含的顶点数。为净水头和机组出力上下限形成的平面区域，其中“×”表示笛卡尔积乘法符号，和分别为机组净水头的下限和上限，分别为机组出力下限和上限。“”表示集合的减运算。 Asafe表示安全运行

区。在上述定义下，限制区约束可表示为：

式中：h、p分别为机组运行时的净水头和出力。

通过上述数学表达，我们将机组限制区约束统一描述为去除不规则限制区的相应安全区约束，从而为我们对不规则限制区识别及自动化建模打下基础。

2.2 限制区约束自动建模方法通过限制区定义可以看出，去除限制区后的安全运行区域本质上是一个可能存在离散，有洞等复杂情形的极度不规则平面区域，如何实现对该区域的MILP自动化建模是本节及本文要解决的主要问题。为此，本文提出一种基于凸剖分算法及凸优化理论和析取规划理论方法的不规则限制区自动化建模化方法。该方法首先需要对不规则安全区进行凸剖分，然后对剖分后的结果采用凸优化理论和析取规划理论进行建模。

2.2.1 安全运行区Asafe的凸剖分 对安全区进行凸剖分是指将不规则安全运行区剖分成若干个互不重叠的凸多边形区域的过程，而且要求这些剖分后的凸多边形区域的并集与安全运行区相等。线性化建模过程实质上是对剖分结果的建模，剖分的结果会直接影响后续线性化建模质量。由于建模过程中引入的整数变量数目等于剖分后凸多边形的个数（见2.2.2节），而整数变量数目又直接影响求解效率，因此为便于MILP求解，需要将不规则限制区剖分成尽量少的凸多边形，这一问题在计算几何中被称为最优凸剖分（optimal convex decomposition，OCD）问题。OCD是典型的NP-hard问题，对该问题已有大量研究[9-10]，其中Hertel-Mehlhorn（HM）算法[10]因其计算复杂度低，且在大多数情形下可找到最优凸剖分结果，被广泛应用到计算机游戏设计[11]、室内导航[12]等领域，本文在此采用HM算法实现对不规则限制区的凸剖分。使用HM算法对安全运行区进行凸剖分流程归纳如下：

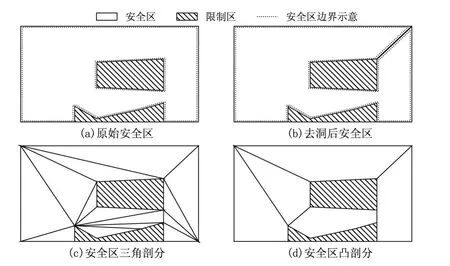
图2 安全区凸剖分示意图

（1）预处理：由于限制区的复杂性，安全运行区可能是由多个多边形组成，每个多边形可能存在单个甚至多个洞（见图2（a）），这些复杂的情形都不适用于HM凸剖分算法，因此需要对其进行预处理。预处理主要包括分离和去洞两个操作。分离是指将包含有多个多边形的情形分离成若干个多边形，之后的所有操作均是对单个多边形的操作。去洞是指将包含洞的分离后的多边形转化为不含洞的简单多边形的过程。该过程首先需要查找所有洞的最右侧点，然后在距离该点较近的多边形点之间进行分割，分割后多边形洞的个数减少1。反复执行该过程，即可去除所有洞[13]。图2（b）为去洞后安全区示意图，从图中可以看出，通过图中右上角线段的分割，安全区不再包含洞。

（2）三角化：三角化是指将分离后的简单多边形划分成若干互不重叠的三角形的过程。该过程采用耳切法（ear clipping，EC）[13]进行处理。对于简单多边形“耳”，指凸点与相邻点围成的三角形，且该三角形内部不可包含其他顶点。如图3所示，图中多边形共包含4个耳，将三角形用其顶点构成的三元元组进行表示，则图中多边形的4个耳分别为（1，2，3）（2，3，4）（6，7，8）（7，8，9）。可以证明，任何超过3个顶点以上的简单多边形必然包括两个以上的“耳”[13]，因此可以通过不断切除多边形耳的方式实现对简单多边形的三角剖分。图2（c）为采用“耳切法”三角化后的安全区示意图。

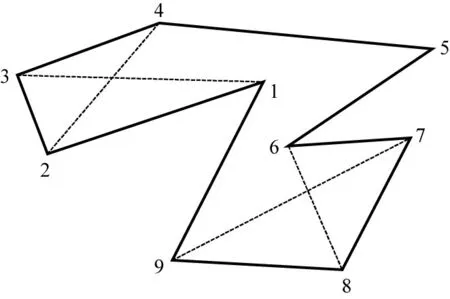
图3 多边形的“耳”

（3）去除非重要对角线：非重要对角线指去除后相邻三角形的并集为凸多边形的对角线，反之为重要对角线。

（4）重复步骤3，直到所有对角线均为重要对角线。在去除非重要对角线后，其他对角线的重要性可能会随之改变，因此需要反复执行步骤2，直到不存在非重要对角线为止。图2（d）为最终所得的安全区凸剖分结果，图2（d）中比图2（c）缺少的对角线，即为去除的非重要对角线。

2.2.2 线性化建模 本节进一步介绍如何根据前文所得的凸剖分结果实现对复杂限制区的MILP建模。为简化表达，首先定义NN为不大于N的正整数集合，其中N为任意正整数。设经过凸剖分后，Asafe被剖分为凸多边形集合根据 Acx，限制区约束（4）可进行如下转化：

式中∨为逻辑“或”运算符号。

i的总边数。根据凸优化理论，凸多边形可以表示成以其各边为界限的半平面的交集[14]，因此Acxi可转化为下式：

式中：ai，j为 Acxi边j的外法向量；bi，j为使上式成立的常数项。

根据式（6），式（5）可进一步转化为：

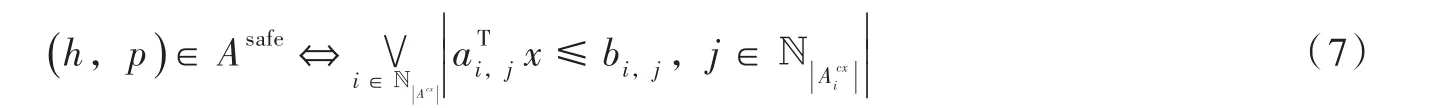
上式中右侧部分为典型的析取式结构，可有效被析取规划方法处理[15-16]。因此进一步引入析取规划建模方法对该析取式进行线性化建模。其中析取式是指由逻辑“或”（OR）运算符号∨连接的若干不等式或等式的关系结构。析取规划方法是研究如何求解析取式约束的通用数学规划方法。通过引入整数变量，将析取式结构转化为求解器可以求解的合取式结构是析取规划中最常用的处理方式。其中合取式是指由逻辑“与”连接的若干不等式或等式结构。析取规划中对析取式转化方法主要分为Big-M（BM）法[17-18]和凸包法两种。其中BM法引入变量相对较少，计算效率通常较高[19]。因此本文引入BM法对式（7）进行线性化建模。

采用BM法进行构建，可得：

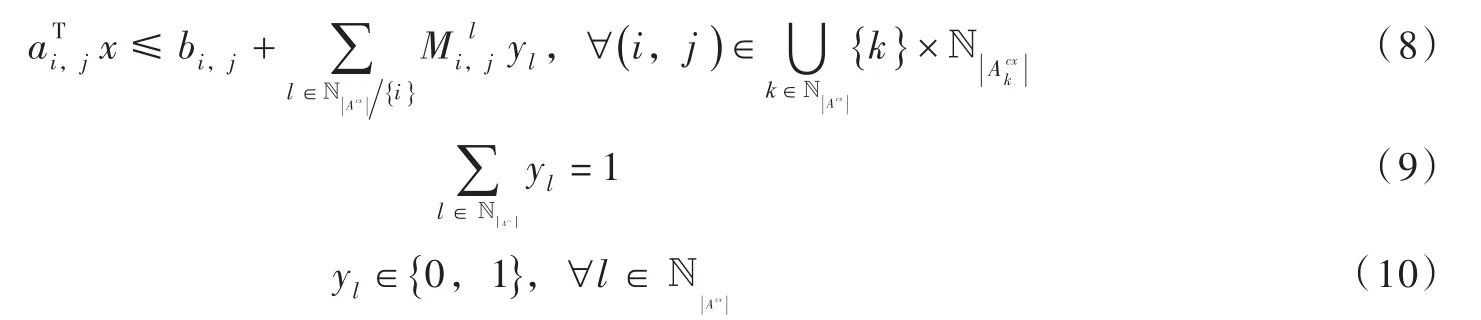
式中：yl为 Acxl的指标变量，如果 yl=1，式（8）中所有i≠l的约束将被BM常数松弛，仅保留i=l的约束项，此时为BM常数。式（8）现代求解器求解MILP问题通常采用分支定界或其变形方法，分支定界法首先求解原问题的线性松弛或部分线性松弛问题，因此其线性松弛问题的可行域与原问题越接近，越有利于问题的求解。显然，较大的BM常数会导致其线性松弛问题可行域过大，从而降低分支定界算法的求解效率。因此，在满足原问题结构的前提下，选择尽量小的BM常数有利于进一步提高算法的求解效率。基于以上，本文BM常数取值方法如下：

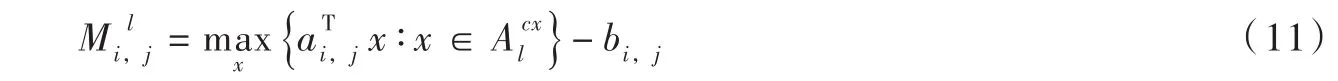
该取值的可行性验证如下：如果 yl′=1，则式（8）中满足i=l′的约束组合等价于式（6），即对于式（8）中i≠l′的式子，将式（11）带入其右手侧常数项可得：

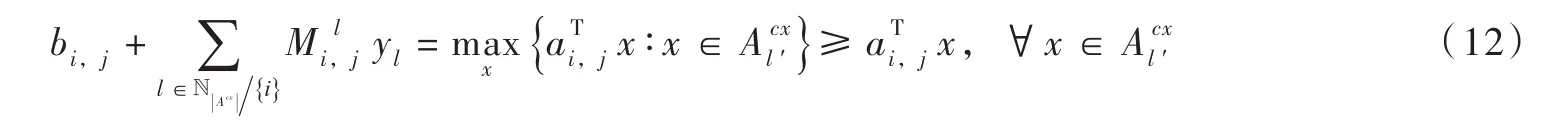
因此，该取值方式满足式（8）结构。显然，任何小于式（11）中的BM取值方法都有可能导致式（12）、式（8）的不成立，因此本文采用的BM值为该构建方法下的最优取值。至此，不规则限制区的线性化模型构建完毕。

3 具有多个不规则限制区的梯级水电站群优化调度模型

为验证本文提出的处理机组复杂多不规则限制区方法的有效性，以调峰任务为目标，对梯级水电站群中多个水电站存在复杂限制区的调度任务进行建模。

3.1 目标函数调峰的目的是尽量使电网剩余负荷平缓，以减少系统整体峰谷差，降低火电等电源的爬坡压力和燃料损耗。本文采用一阶平均距作为目标函数以平缓剩余负荷。

式中：r、R为电站编号和电站总数，并规定编号较小者位于上游；t、TI为调度时段编号和总时段数，本文TI设置为24；u、Ur为机组编号和电站r的机组总数目。如无特殊说明，下文中r、t、u为下标时，均为电站，时段及机组编号；p′r，u，t为电站r机组u在时段t的出力；Dt、D′t分别为时段t的系统负荷和减去水库调峰负荷的系统剩余负荷；----D′为系统剩余负荷平均值。上述形式无法直接采用求解器求解，本文引入辅助变量δt做如下等价转换：

3.2 常规约束常规约束指水电机组组合问题中除了限制区约束以外的其他常见约束。

（1）水量平衡方程：

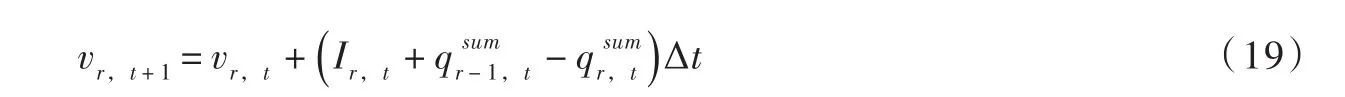
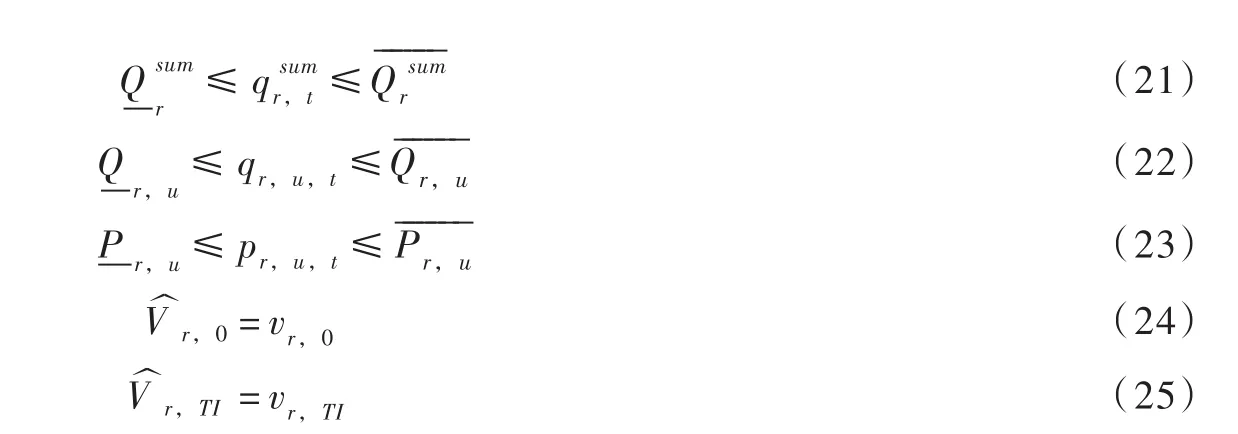
式中：qr，u，t表示机组开机时段平均发电流量;为时段末库容下限及上限值；为时段平均出库流量下限及上限值；为开机时段平均发电流量下限及上限值；为时段平均出力的下限和上限值。表示调度期初和末库容是给定的。以上为机组开机时各变量的边界约束，而机组实际出力和实际发电流量仅在开机时需要满足上述约束，关机时需要设置为0。首先定义0-1机组状态变量yr，i，t，如果yr，i，t=1表示相应机组处于开机状态，否则 yr，i，t=0。则上述情形可以描述为下列各式：

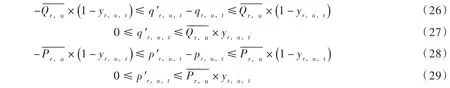
式中：q′r，u，t为机组实际时段平均发电流量。式（26）、式（28）分别表示处于开机状态时，机组实际发电流量（出力）等于机组开机发电流量（出力），若处于关机状态，这两个约束将被松弛。式（27）、式（29）表示处于关机状态时，机组实际发电流量和出力必须为0，若处于关机状态这两个约束将被松弛。

（3）机组开停机持续时段约束：定义二元机组开机操作变量 gr，u，t，若 gr，u，t=1表示该机组在该时段进行开机操作，否则 gr，u，t=0。定义机组关机整数操作变量dr，u，t，若dr，u，t=1表示该机组在该时段进行关机操作，否则dr，u，t=0。则机组开停机约束可表示为：

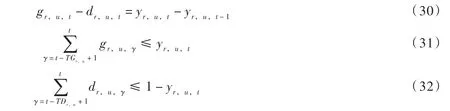
式中TGr，u、TDr，u分别为相应机组的最小开机和关机持续时段数。

（4）电站出库约束：

（5）净水头相关约束：本节介绍与净水头计算相关的约束。

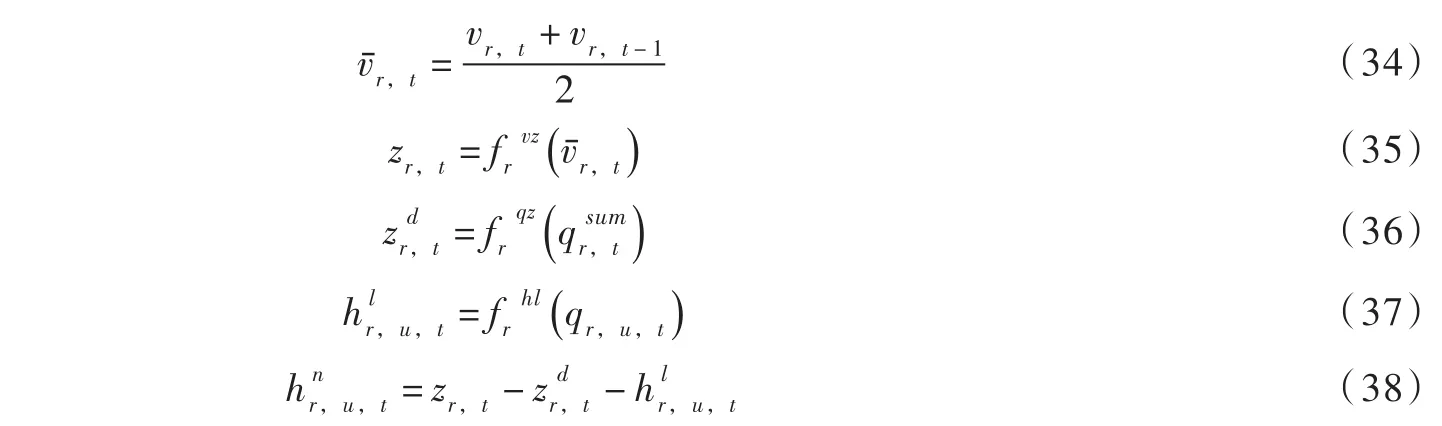
（6）机组动力函数约束：

式中φr，u为机组动力性能函数。

3.3 限制区约束

3.4 常规约束构建方法常规约束中式（35）—式（37）为一维非凸非线性曲线约束，式（39）为二维非凸非线性曲面约束。这两类约束无法直接利用求解器求解，需要进行线性化处理。而这两类约束线性化已有大量成熟方法，本文对于一维非线性约束及二维非线性约束均采用文献[8]中所述方法，在此不再赘述。

4 应用实例

为验证本文所提方法的合理与有效性，选用中国西南地区W流域干流梯级水库系统中包含复杂不规则限制区的高水头巨型水库A和水库B作为重点研究对象。W流域梯级水库系统总装机达8 GW，最高水头达到200 m，是我国的十三大水电基地之一。水库A和水库B是流域中总装机最大的两座高水头巨型水库。其中水库A位于上游，调节性能为季调节，共包含5台机组，总装机达1250 MW，最高水头为140 m。水库B位于梯级系统的下游，为多年调节水库，共包含5台机组，总装机达到3000 MW，最高水头达200 m。其中水库A所有机组，水库B中除4#机组外其他机组均含有大范围不规则限制区。选取某年7、8、10、11月份某典型日实际数据进行一日24点模拟计算，其中7、8月份方案作为汛期代表，10、11月份方案作为枯期代表。所有方案的最小开停机约束均为4 h。

表1 方案主要参数

各方案其他主要参数见表1。为进一步降低搜索空间提高求解精度和效率，表1中净水头范围采用净水头动态设置方式确定，具体方法如下：

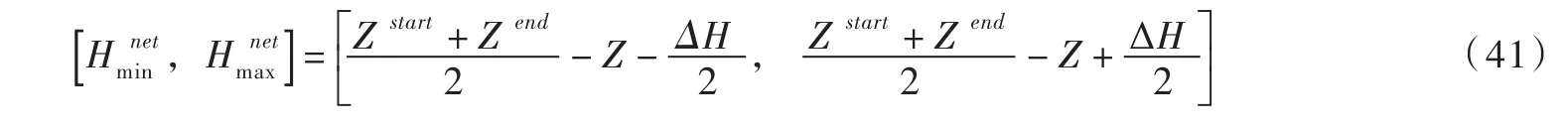
本文算法及模型构建均采用Python3.6语言编写，程序运行的操作系统为Ubuntu16.4虚拟机，硬件配置为Inte（lR）Xeon（R）CPU E7-4850 v3@2.20GHz 96 logic CPU，32G RAM，并调用Gurobi8.1求解器分支定界算法进行求解，凸剖分涉及的计算几何相关基础算法采用Shapely[20]和PolyPartition[21]等开源库中的相关算法。模型中对常规非线性约束进行线性化时，尾水位泄量约束、机组性能曲线约束各变量方向分段数设置3，水头损失曲线分段数为4。对于巨型水库，其一日内的水位变幅相对较小，因此本文仅在始末水位上下1m的范围内进行离散，分段数设置为1。设置算法的停止准则为运行时间达到1800 s或gap值达到0.02。其中gap值指当前最优可行解和最优值下限的相对差值，gap值是描述当前解最优性的指标，gap值越小说明当前值与理论上的全局最优值越接近。

4.1 凸剖分结果分析图4为水库A及水库B各机组的安全运行区及其凸剖分结果示意图。值得注意的是，采用动态净水头区间设置方法后，其安全运行区会随着净水头搜索区间的改变而改变。搜索区间越小，相应安全运行区越小，因此方案计算过程中采用的安全运行区要小于图4所示的安全运行区。不失一般性，本节仅给出在设计最大净水头和最小净水头之间的安全区的剖分结果图。可以看出，安全运行区呈现出了高度不规则甚至有洞等特性。其中水库A中1#—3#机组，水库B中1#—3#及5#机组存在不止一个不规则限制区，此时安全运行区的不规则性更加显著。水库B的1#—3#及5#机组在多限制区影响下，呈现出有洞的特性。水库A中4#机组在水头位于[112，129]时，存在一块规则限制区，但在更大的区域内，安全运行区仍然具有不规则性，以往研究往往显性或隐性假设机组运行不会超出该规则限制区的水头范围，这在大多数情况是成立的，但在某些时段机组仍有可能在超出规则限制区运行水头范围内运行，那么针对规则限制区的建模不再适用。水库B的4#机组不包含限制区，因此其运行区为完整的一块矩形区域。从剖分结果看，在离散、有洞、多不规则限制区、部分规则限制区影响下，算法均可以有效将安全运行区凸剖分为若干互不重叠的凸多边形，这体现出凸剖分算法的通用性。

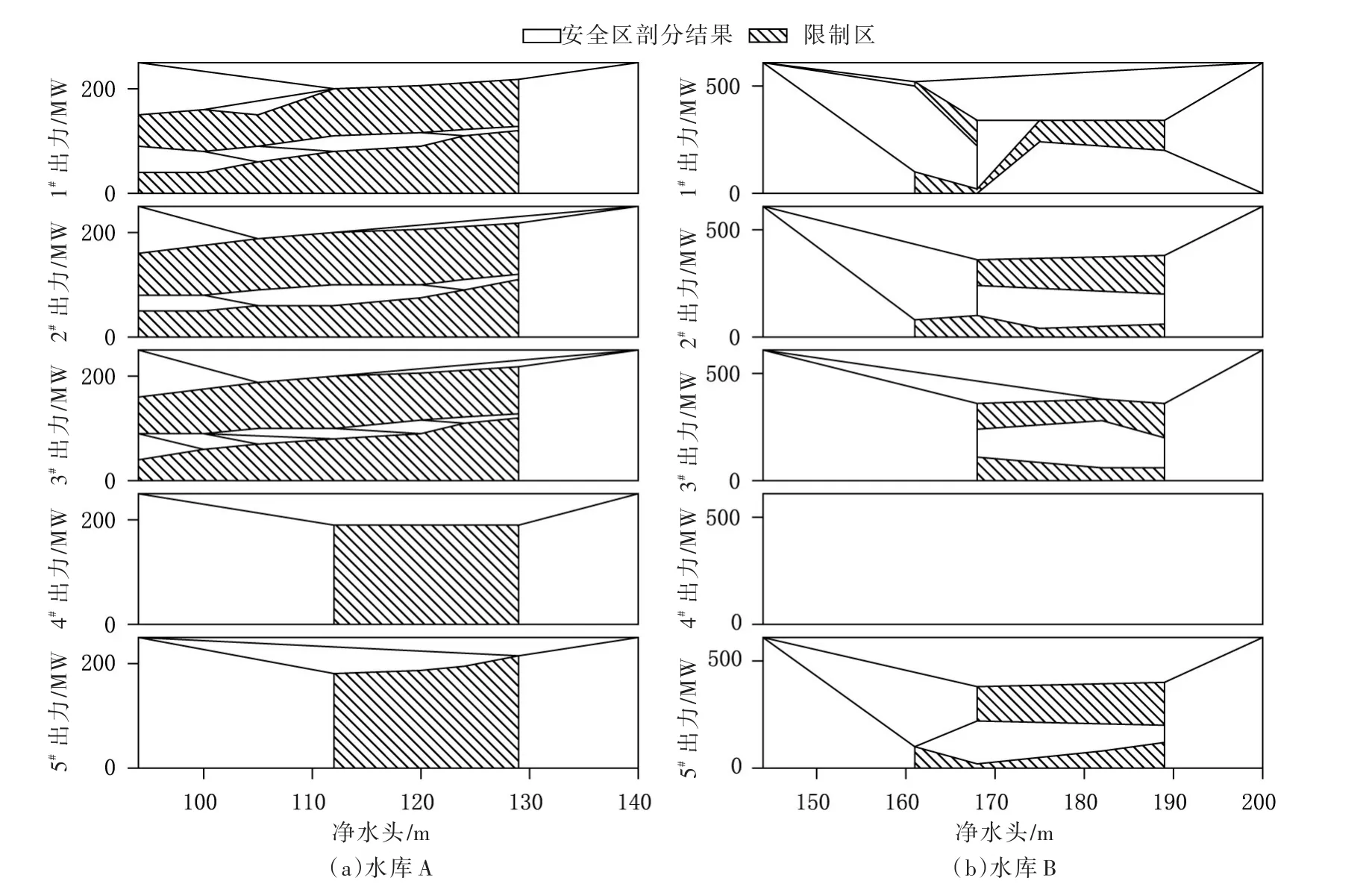
图4 水库安全运行区及其凸剖分结果

4.2 计算结果及调峰效果分析各月份方案计算结果见表2。从表中可以看出，汛期方案整体耗水量和发电量多于枯期方案。从变量及约束数量看，4个方案中连续变量均为3599个。不同方案之间离散变量个数及约束个数不同，这是由于采用了动态净水头搜索区间后，安全运行区也会动态的随之改变，从而导致安全区剖分结果及线性化结果的不同。从结果gap值及计算时间看，4个典型方案均在给定时间内求出了近似最优解，其中汛期方案的gap值达到0.02，枯期方案中10、11月份的gap值也达到0.04和0.05。在实际应用过程中，对求解时间敏感的场景下，可以通过降低最大求解时间的方式或提高gap限制值的方式，减少总计算时间。相应的，对结果最优性要求较高的场景，则可以通过增加最大求解时间及进一步降低gap的方式，以期得到更优的解。

表2 各月份方案计算结果

从图5中直观看出，4个方案均达到较为显著的削峰效果。水库A和水库B的发电过程也较好响应了调峰需求。进一步的，各方案结果的具体调峰指标值如表3所示。表中表示原负荷的平均爬坡，表示剩余负荷的平均爬坡。这两个值能够体现负荷过程的整体光滑程度，其越小则认为越平滑，也越有利于火电运行。表示平均爬坡的减少比例。从表3中可以看出，汛期两方案的峰谷差减少比例分别达到0.65和0.70，平均爬坡减少比例也分别达到0.54和0.63。枯期两方案由于整体发电量较少，调峰效果相较汛期方案相对较差。枯期两方案峰谷差相对减少比例为0.24和0.35，平均爬坡减少比例也达到了0.11和0.35。由此可以看出，本文的调峰模型可以有效削减峰谷差，使调峰结果更加平缓。

图5 各方案调峰效果

表3 各方案结果调峰指标值

4.3 限制区规避效果分析本节分析本文所提模型计算结果对限制区的规避效果，并与常规计算模型进行对比。其中常规计算模型指不考虑限制区约束的短期调峰模型。如图6、图7所示，本节分别选择8月份和10月份方案作为汛枯期代表进行分析。图中本文模型限制区指本文模型计算的运行过程中各时段机组平均净水头对应的出力限制区，常规模型限制区同理可得。从图6中可以看出，常规模型由于没有考虑限制区约束，在水库A的3#机组，水库B的2#和5#机组均出现落入限制区的情况，从而对电厂及电网的安全造成威胁。而本文模型在各个时段均避开限制区。在汛期电网用电高峰时刻，各机组也以接近装机容量的状态进行发电，以满足电网的调峰需求。对于枯期10月份方案，从图7可以看出，常规模型在水库A的2#、3#机组，水库B的1#、2#、5#机组出现了长时段运行在限制区的情况。本文模型计算结果均满足限制区约束，保证了电站和电网的安全稳定运行。综合对比图6和图7的出力限制区过程可以看出，在不同运行条件，甚至同一日内出力限制区都发生剧烈变化，传统规则限制区考虑方式不再适用，对其的简化也势必造成误差从而增加落入限制区的风险。综上，本文所提模型可以有效考虑水电机组复杂限制区约束，在保证电厂电网安全运行的前提下，充分发挥水电的调峰能力。

图6 8月份方案本文模型和常规模型计算结果对比

图7 10月份方案本文模型和常规模型计算结果对比

5 结论

针对制约影响我国西南地区水电安全经济运行的高水头巨型机组复杂多不规则限制区瓶颈问题，本文提出了自动解析处理机组复杂限制区的建模优化方法，该方法结合了计算几何凸剖分理论、凸优化理论、析取规划方法及MILP数学规划方法，并通过西南某干流梯级水电站群实际资料进行了验证，结果展现了方法的有效性。由于所提方法不需要对复杂不规则限制区进行人工预处理，完全根据限制区的数学定义实现自动剖分，达到了自动建模与求解的效果。因此，解决了区域、省级电网大规模水电系统复杂不规则限制区自动优化建模难题，这对于将来响应电网差异化、自动化调度应用，响应市场化条件下的水电出力频繁变化的新情况，意义特别重大。