海拔高程对泄洪雾化影响的敏感分析

柳海涛，徐建荣，孙双科，彭 育

（1.流域水循环模拟与调控国家重点实验室，中国水利水电科学研究院，北京 100038）（2.中国电建集团 华东勘测设计研究院有限公司，浙江 杭州 311122）

1 研究背景

大型水电站泄洪雾化对于工程安全与周边环境有重大影响[1-4]，如何评估与防范雾化危害，是水利水电工程设计中的重要研究课题之一。泄洪雾化的本质是水团、水滴以及水雾在大气中的运动，其中水舌入水激溅占据主导地位，由此构成了雾化降雨的主体。国内目前主要采用随机溅水数学模型对雾化降雨进行分析[5-8]，该类模型通过描述每个水滴在空气中的运动过程，同时考虑空气阻力、浮力、重力等条件，求得雾化溅水区内下垫面降雨强度分布。上述模型在计算中主要考虑泄洪水力学条件与地形条件的影响，对于海拔高程与气象条件的影响尚未考虑。

目前我国水电工程建设与运行已从低海拔地区发展到2000 m以上高海拔地区，泄洪雾化与气象环境之间相互影响不容忽视。从定性的角度看，海拔高程对于雾化降雨的影响，主要体现在三个方面：（1）不同海拔地区大气压强不同，从而影响水流掺气、扩散过程，引起雨雾总量发生改变；（2）不同海拔地区空气密度与黏滞系数不同，使得雾化水滴在运动中所受阻力、浮力等作用发生改变，引起雾化降雨分布发生改变；（3）不同地域气压与空气密度的差异，使得的泄洪雨雾输运与沉降过程发生改变，最终影响外围雨雾浓度分布规律。

针对上述问题，需通过不同海拔地区对比试验、原型观测、理论分析、数学模型等手段进行系统研究。鉴于问题的复杂性，本文仅针对海拔高程对于雾化降雨分布的影响，开展探索性研究。通过理论分析，在前人研究的基础上，建立考虑当地海拔高程影响的泄洪雾化降雨随机溅水数学模型，结合实际工程雾化原型观测资料，进行数学模型计算验证。然后，针对不同海拔高程条件下，泄洪雾化降雨分布的变化规律进行敏感性分析，为今后全面考虑气象条件对于泄洪雾化过程的影响，奠定理论研究基础。

2 随机溅水数学模型的基本理论

将泄洪水舌入水喷射过程视为一种随机喷射现象，采用拉格朗日方法，对喷射水滴在空气中的运动进行跟踪，然后通过统计方法求得溅水区内下垫面上的降雨强度分布。

2.1 水滴运动的微分方程水滴在运动过程中，受到重力、浮力和空气阻力的共同作用，由此建立水滴运动的力学微分方程：

式中：u、v、w为水滴在空间坐标[x、y、z]处的运动速度，m/s；uf、vf、wf分别为水滴邻近风速，m/s；Cf为阻力系数；d为水滴粒径，m；ρa为空气密度，kg/m3；ρw为水的密度，kg/m3；g为重力加速度，m/s2。求解上述方程组需给定水滴初始喷射条件，然后采用4阶Runge-Kutta法[9]进行数值求解。

2.2 水滴随机喷射条件

（1）水滴直径d采用概率密度函数分布[8]：

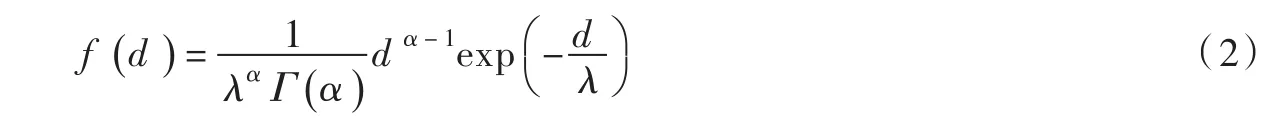
（2）水滴初始喷射速度u采用概率密度函数分布：

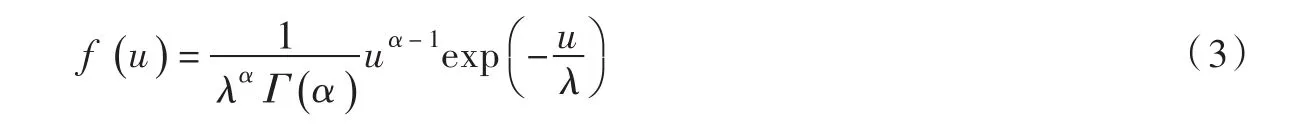
（3）水滴出射角θ采用概率密度函数分布：

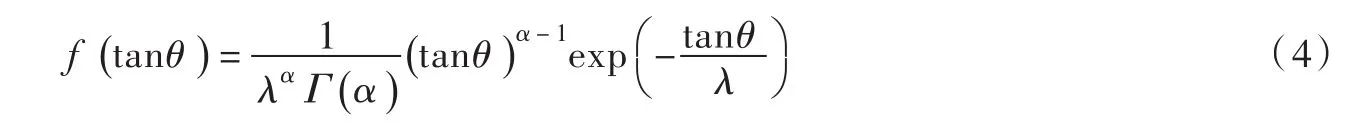
（4）水滴出射偏转角φ采用概率密度函数分布：

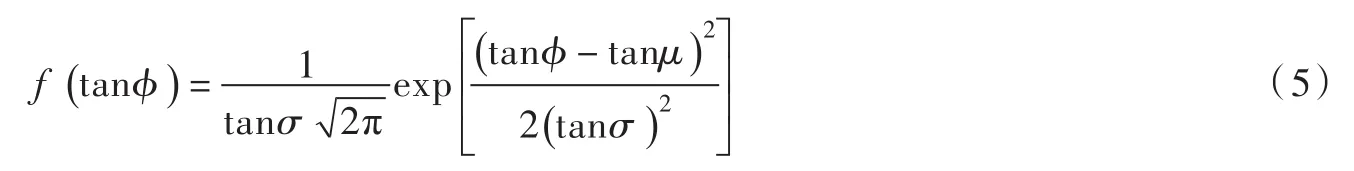
式中：μ为偏转角众值，依据水舌平面偏转角度取值；σ为偏转角的均方差，σ取值在20°～30°之间，本文取22.5°。

（5）水滴喷射速度与角度的众值采用下式表示[10]：

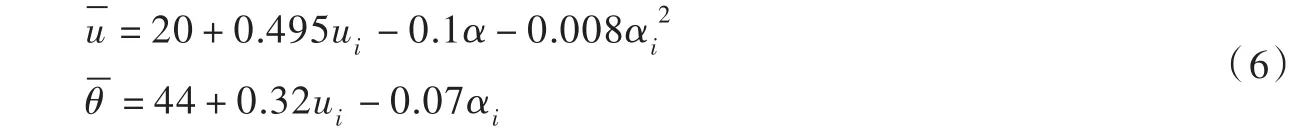
（6）水滴喷射颗粒流量n：

水舌入水激溅主要发生于入水前缘，其喷射厚度h可以表示为[11]：

式中：η为系数，可取25；C为含水浓度，可根据水舌入水时断面形态判断，一般地，对于充分发展的掺气水舌，一般在0.03左右；v为水的运动黏滞系数，m2/s；R为水力半径，m；u*为摩阻流速，m/s，其表达式为其中τ为空气阻力

水舌入水喷射的总流量可进一步表示为：

式中：ks为喷溅系数，ks=0.01～0.03，本文取0.01；l为水舌入水前缘总长度，m。

一旦喷射总流量确定，则对应的水滴颗粒流量可以表示为：

式中dm为整个喷射过程的水滴平均粒径，该粒径值未知且不同于粒径众值。为此，本文模型首先计算粒径众值对应的颗粒流量然后，由式（2）中概率密度函数，随机生成个喷射水滴其对应喷射总流量为最后，式（8）中总流量对应的颗粒流量修正为

通过上式（2）—式（9），可以随机生成一组喷射水滴，作为初始条件，运用式（1）计算每个水滴的运动过程。

2.3 海拔高程对于水滴运动的影响海拔高程与气温的变化，会引起空气密度、气压、黏滞系数、阻力系数的变化，最终引起泄洪雾化降雨分布发生变化。

（1）水滴运动阻力系数 Cf采用下式表示[12]：

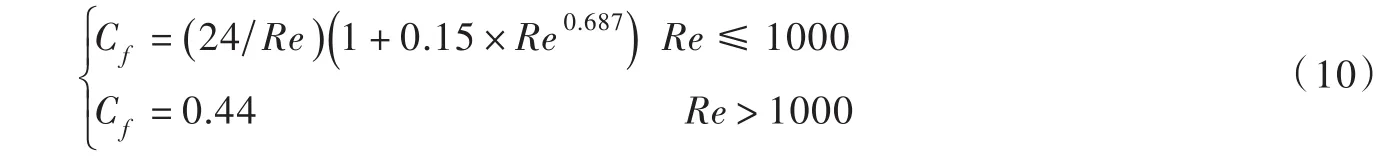
（2）空气运动黏滞系数 va采用下式表示[13]：

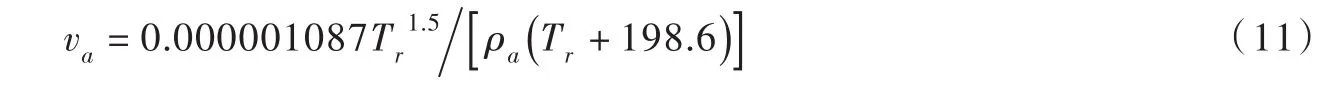
式中Tr为兰氏温度，oR，可表示为Tr=1.8Ta+491.67，Ta为空气温度，℃。

（3）空气密度ρa与海拔高程、气温的关系可用下式表示：

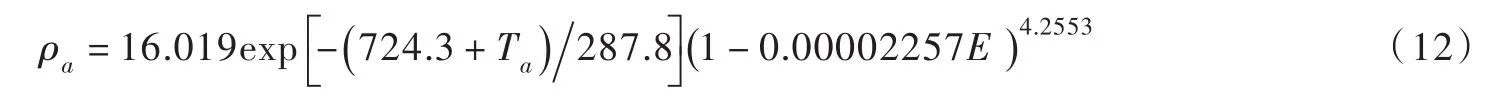
式中E为海拔高程，m。

（4）当地气压p与海拔高程E、气温Ta的关系采用下式表示：

式中：p0为海平面标准气压，取101 325Pa；cp为空气定压比热容，取1005 J/（kg·K）；M为干燥空气的摩尔质量，取0.02896kg/mol；R0为普适气体常数，取8.315 J/（mol·K）。

将上式（10）—式（12）与式（1）联立求解，可以考虑工程当地海拔与气温对于雾雨运动过程的影响。由于水舌风与雾化降雨相互伴生，不可分割，以往的研究对于水舌风场多采用正态分布假定或者均一化假定处理。对此，本文通过将三维水舌风场转换为结构化数据，然后实时求解水滴瞬时邻近风速，用于闭合式（1）中水滴运动方程，从而较全面考虑河谷中复杂风场对于雨雾运动过程的影响。

2.4 溅水模型的数值计算方法

（1）喷射时间的离散。在溅水过程中，水滴分布于整个空间，只有当水滴到达地面时才能形成降水。为此，在本文模型中，首先，根据水滴自由抛射后在空中的最长停留时间t，确定溅水喷射总历时T，一般应满足T≥2t；然后，将计算时间划分为m个时间步长dt，假设在喷射历时T内的水滴总量为N=Tn，n为水滴喷射颗粒流量，则每个步长内的水滴总量为Ni=N/m；第三，运用4阶龙格-库塔法求解每个时间步长内水滴的运动方程，其中对于第i个步长内的Ni个水滴，其最长飞行历时为

（2）降雨强度的计算。降雨强度定义为一定时间内穿过单位面积平面的总水量除以降雨历时。为此，本文模型中，首先将喷射区域内地面离散为小尺度的集雨网格，然后在每一个时间步长dt内，判断Ni个水滴的垂向位置，若其在n-1时刻位于地面高程以上，而n时刻位于该平面以下，则表明水滴已降落地面，此时根据其平面坐标，将其水量计入相应的集雨网格，即有Volume=Volume0+πd36，同时该水滴的飞行终止。由于采用随机函数模拟水滴出射条件，模型需要重复M次喷射过程，当所有M次喷射过程计算完成后，统计平面上每个网格内积累的水滴总体积，再除以喷溅历时T、网格垂直投影面积A与重复次数M，即可得到该网格内时均降雨强度分布P=Volume/(M AT)。

（3）水滴运动过程中风速与地形的影响。模型求解水滴运动方程中，需要获取水滴邻近风速与地面高程，前者用于求解水滴所受风场加速度，后者用于判断水滴是否降落地面，从而反映两者对于雾化降雨分布的影响。为此，本文模型中，首先采用相对成熟的Fluent软件求解三维河谷风场，然后通过相应的转换程序，将非结构化的三维风场与地形数据转换为结构化的风场数据Wind(i , j,k)及地形数据[T o po(i , j)]，其中i、j、k为三维结构化坐标，为节省空间，上述数据以二进制文件存储；随机溅水模型运行初始，先读取上述风场与地形数据，并按照其结构化坐标存储在相应的数组单元中。对于空间任意水滴，若要获取其邻近风速，可通过对其瞬时坐标（x,y,z）数值取整，找到其相邻的8个结构化坐标[Ii,Ji,Ki]，i=1～8。根据其结构化坐标，直接从对应数组单元读取相应的风速数据，然后插值得到水滴的邻近风速Ufki为空间插值函数。同样地，采用二维空间插值方法可以求得水滴的邻近地面高程。

（4）数值振荡的抑制。从水滴运动微分方程得知，式（1）中右端项为水滴所受的运动加速度，其阻力项的量值与水滴粒径成反比，由于采用随机函数模拟，水滴喷射粒径为一随机变量，当某一水滴粒径趋近于0时，该水滴所受阻力加速度则趋于无穷大，水滴运动则产生数值振荡。从理论上分析可知，单位时间步长内，水滴所受的最大加速度可表示为UT为水滴终极速度，U0为水滴初始速度，dt为时间步长。在水平方向上，水滴终极速度UT=U0，即为当地风速；在垂线方向上，水滴终极速度为即为重力、浮力、阻力达到平衡时速度。当水滴初始时刻所受的运动加速度为a0≥amax，表明水滴运动速度在该时间步长中已经达到稳态，则在该时间步长中，令a0=amax，下一时间步长中，水滴初始速度U0=UT。

3 数学模型验证分析

3.1 计算条件中电建昆明院科研所于2014年8月17日，针对小湾水电站泄洪洞全开泄洪过程，水舌入水形态与泄洪雾化进行了原型观测。观测过程中，坝上水位1236.32 m，实测泄洪流量3500 m3/s，当地海拔1000 m，气温20℃，观测时间50 min。泄洪洞实地泄洪雾化情况见图1，水舌入水形成的雨雾在泄洪风场作用下沿两岸爬升，高度接近300 m，通过沿岸布置雾化降雨测点，得到了下游降雨强度的实测点据。本次观测工况中泄洪水舌入水条件如表1，水舌入水位置及下游河谷地形见图2。

图1 小湾电站泄洪洞全开雾化情况

3.2 水舌风场计算结果泄洪水舌入水过程中，在河谷中形成局部风场，对雾化降雨分布范围产生影响。根据当地海拔与气温条件，由式（11）—式（13）求得当地大气黏滞系数1.6791×10-5m2/s，大气密度1.0805 kg/m3，大气压强89 999.2 Pa。然后，基于Fluent软件，求解泄洪洞水舌下游河谷风场。计算中采用了RNGk-ε模型封闭连续与动量方程[14]，水舌入水断面采用速度边界，周围河谷地形按照标准壁面函数进行处理，顶部为压力出口边界。图3为计算得到的河谷地面附近风速等值线图。由图可知，河谷泄洪风场受到入水条件与地形的影响，在水舌入水附近风速可达50 m/s量级，然后向外围逐步衰减，纵向影响范围可达下游1500 m，两岸爬升高度超过300 m，其复杂形态对于雾化降雨分布将会产生影响。

3.3 降雨强度分布计算结果根据泄洪水舌入水条件、泄洪风场以及当地气象参数，采用随机溅水数学模型进一步计算河谷中雾化降雨分布形态。图4为泄洪洞下游雾化降雨强度分布形态，由图可知，雾化降雨分布受到风场与地形的影响，雾化雨区在两岸爬升高度约250 m，纵向分布范围受到下游右岸河谷地形的阻挡，边界位于泄洪洞下游880 m。图5为泄洪洞下游雾化降雨强度等值线图，为便于比较，将原型观测点据一并汇出（图中方框数据），结果表明两者在分布规律上甚为吻合。

表1 泄洪洞水舌入水条件

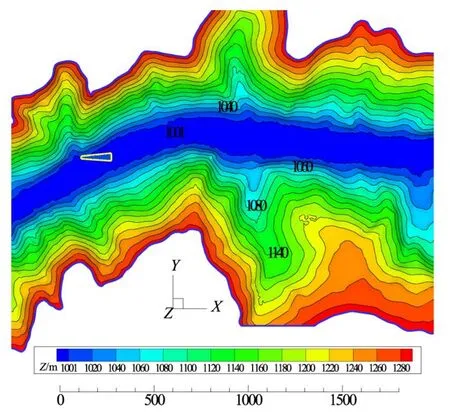
图2 小湾泄洪洞水舌入水位置与河谷地形等高线

图3 小湾泄洪洞下游地面附近风速分布

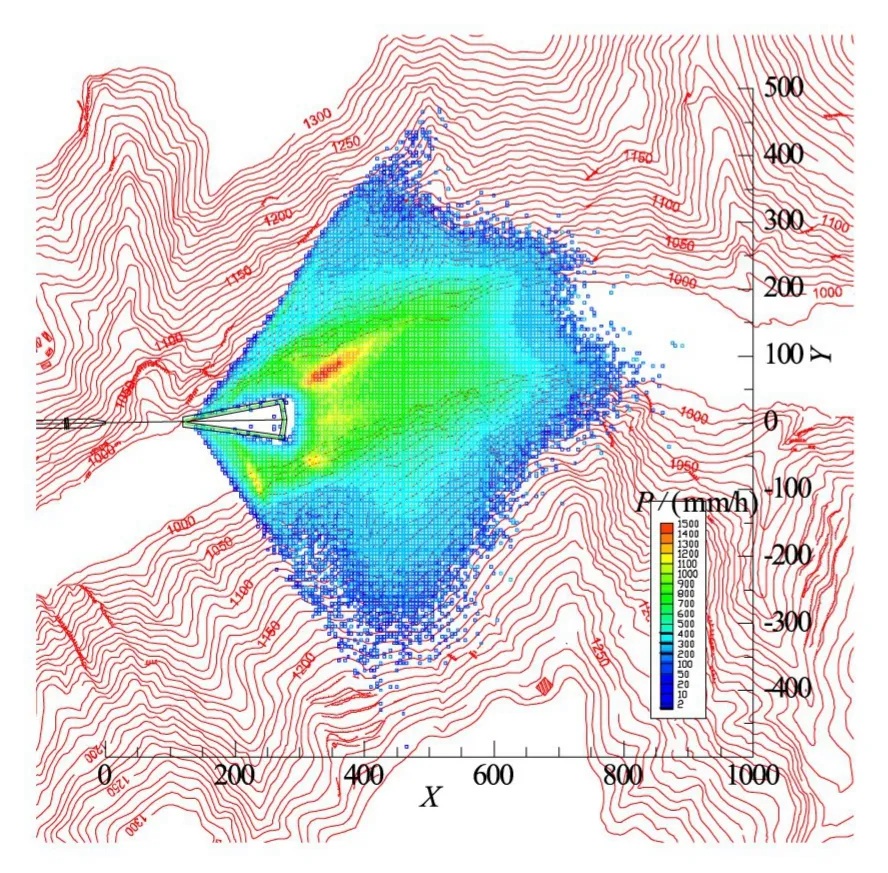
图4 泄洪洞雾化降雨分布形态

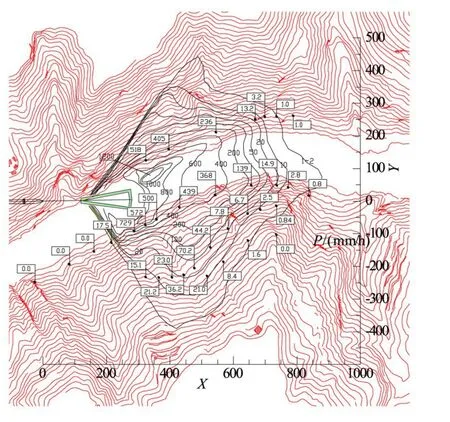
图5 泄洪洞雾化降雨强度分布

表2 不同海拔地区气象因子计算结果

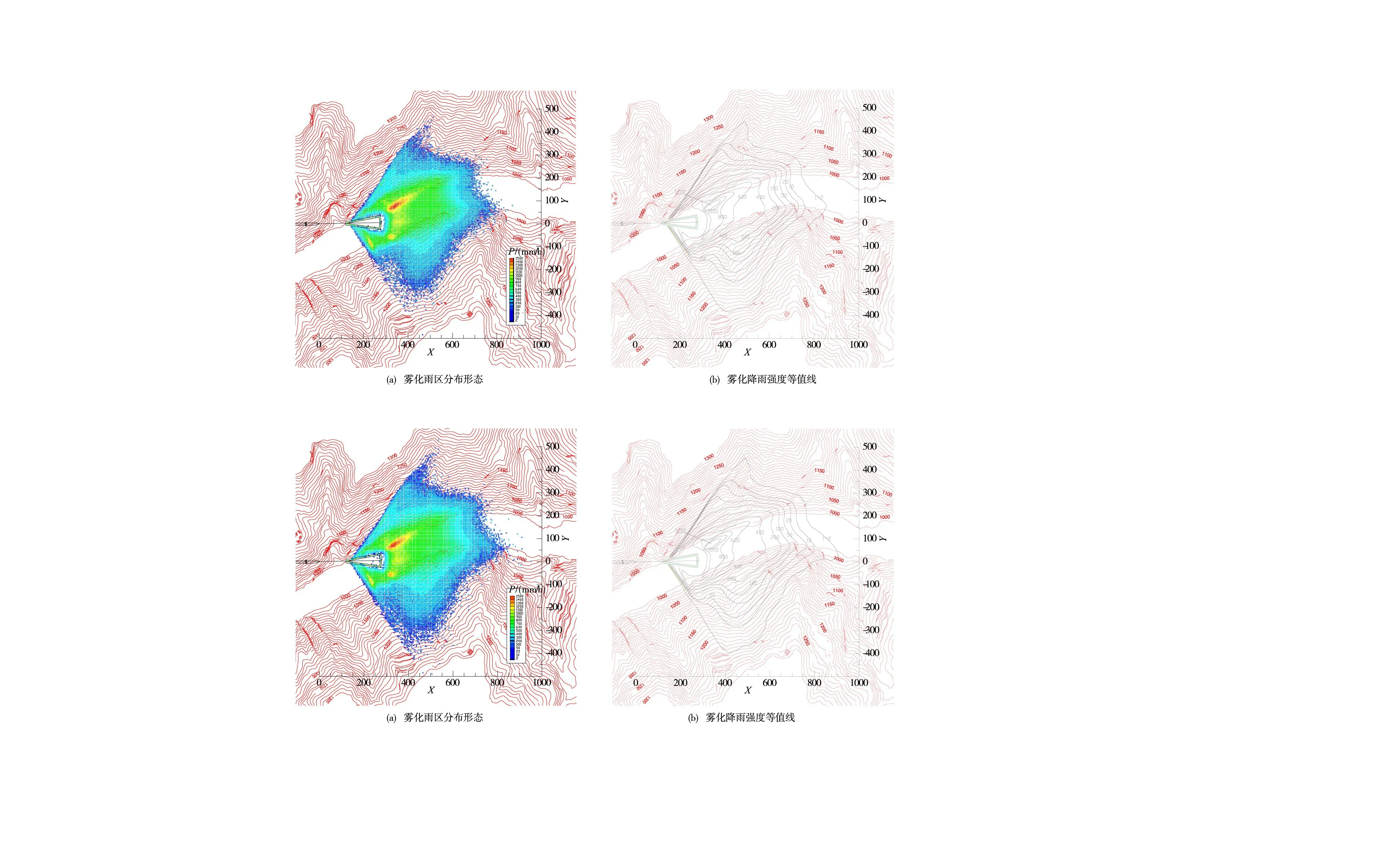
图6 海拔高程50m条件下泄洪洞下游雾化降雨分布

3.4 海拔高程对于雾化降雨影响的敏感性分析小湾电站当地海拔高程约1000 m，为分析海拔高程的影响，本文在泄洪条件、河谷地形、当地气温均不变的前提下，研究不同海拔高程50 m、2000 m、3000 m情况下，泄洪雾化降雨分布的变化规律，上述海拔高程对应的气象参数见表2。图6—图8为不同海拔高程条件下，泄洪雾化降雨分布计算结果，结果分析表明：（1）随着海拔高程的增加，在相同的泄洪条件下，泄洪洞下游雾化降雨区分布范围会有所增加。当海拔高程50 m时，两岸雨区爬升高度约190～220 m，纵向边界位于泄洪洞下游约850 m；而当地海拔高程3000 m时，两岸雨区爬升高度可达230～280 m，纵向边界位于泄洪洞下游950 m，若非受到右岸地形的阻挡，雨区纵向变化范围会更大。（2）随着海拔高程的增加，雾化降雨强度分布规律发生坦化。表3为雾化降雨强度沿河谷纵向的分布数据，由表可知，在大于400 mm/h的等值线区域，分布范围有所减小，而在小于400 mm/h的区域，分布范围有所增大。（3）海拔高程除了对雾化降雨分布产生影响以外，还会对泄洪雨雾总量以及雨雾输运过程产生影响，此外气温条件也是重要的影响因素，对此需要进一步开展系统研究。

图7 海拔高程2000m条件下泄洪洞下游雾化降雨分布

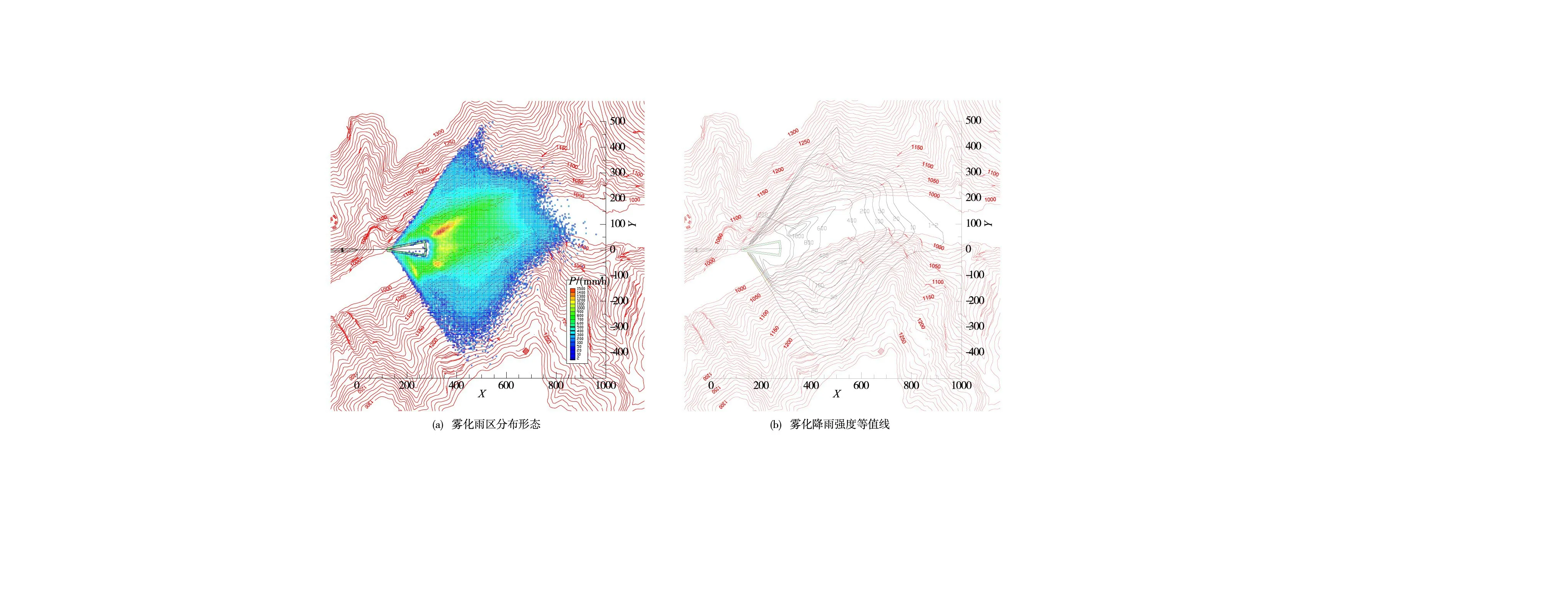
图8 海拔高程3000m条件下泄洪洞下游雾化降雨分布

表3 泄洪雾化降雨强度沿河谷纵向的分布数据

4 结语

本文通过理论分析，建立了考虑海拔高程与气温条件影响的泄洪雾化随机溅水数学模型，结合小湾电站泄洪洞雾化原型观测数据进行了验证，两者数据吻合良好。在此基础上，针对不同海拔高程条件下，泄洪洞下游雾化降雨分布变化规律进行敏感性分析。在泄洪条件、地形、气温不变前提下，随着海拔高程的增加，泄洪洞下游雾化降雨区分布范围会有所增加，同时雾化降雨强度分布规律发生坦化，证明海拔高程对于雾化降雨强度分布的确存在一定影响。本文研究仅针对泄洪雾化降雨过程，下一步拟对水舌激溅总源量以及雨雾输运过程，继续开展海拔高程与气温条件的影响分析。