康普顿成像系统角分辨影响因素的理论及模拟研究

王 薇，李传龙，吴建华，李兴隆

(中国原子能科学研究院 辐射安全研究所，北京 102413)

康普顿成像系统从提出距今已有40余年[1]，相比于传统的机械准直单孔成像系统，具有诸多优点[2]：首先，康普顿成像系统无需准直器，增加了系统的灵敏度和视野范围，可设计为多层以提高探测效率，从而使其测量时间短、系统质量轻、环境适应性强；其次，由于大部分材料在几百keV～几MeV能区内的康普顿散射截面较大，因此康普顿成像系统更适用于对能量为几百keV～几MeV的γ射线成像；再次，康普顿成像系统的成像分辨率取决于探测器的能量和位置分辨本领，成像效率取决于探测器的尺寸、材料和几何，成像分辨率与成像效率无相互制约关系，可同时得到改善。另外，其可在一定成像范围内对未知源实现三维成像[3-4]，即能精准确定放射源所在位置的空间角度和纵深距离，这种对源的全方位识别能力在各种核材料检测、核设施退役场所强辐射场的热点定位及放射医学[5]中显得尤为重要。

随着放射医学手段的普及、核设施退役工作的展开及对核与辐射源事故处理技术要求的不断提高，具有上述诸多优点的康普顿成像系统成为近年来国内外的研究热点[6]。其中以文献[7-10]研制的康普顿成像系统最为突出，2001年开发了由两块1 cm3位置灵敏CZT晶体分别作为散射和吸收探测器的康普顿成像系统，该系统的成像角分辨率约为3°(511 keV)和2°(1 MeV)，成像效率约为1.5×10-4(500 keV)和8.8×10-6(3 MeV)；2004年开发了由1块1.5 cm×1.5 cm×1 cm像素型CZT晶体同时作为散射和吸收探测器的康普顿成像系统，该系统的成像效率接近2%，成像角分辨率约为17°(662 keV)，其最大优势在于可进行4π视角全方位成像，近年以该成像系统为原型推出了商业化康普顿相机H3D Polaris-HTM，其高配置版本Quad采用了19.4 cm3像素型CZT晶体进行4π成像，探测时间缩短至普通版的1/3，成像角分辨率约为30°(实时处理)。国内康普顿相机的研制起步较晚，其中四川大学与中国工程物理研究院对阵列式康普顿相机进行了模拟及反投影图像重建[11-13]，但关于康普顿相机成像的理论设计研究及实际样机研制尚未见报道。本文模拟构建由位置灵敏CZT晶体组成的双层康普顿成像系统，对引起成像系统散射角误差进而影响其角分辨能力的因素开展理论研究，推算不同能量光子入射时由不同角分辨影响因素引起的散射角误差范围，提出成像系统的优化设计建议。

1 康普顿成像原理

康普顿成像系统利用康普顿散射原理来成像[14]，一般要求入射光子与探测介质先发生康普顿散射，将部分沉积能量传递给介质中的电子，并测量记录反冲电子的动能T′e和相互作用位置x1；产生的散射光子继续与探测介质发生光电吸收，沉积全部能量，此时测量记录散射光子的能量E′和相互作用位置x2。对满足上述条件的入射光子能量E0可表示为：

E0=T′e+E′

(1)

考虑到实际中高能γ射线入射时产生的散射光子可能会继续发生康普顿散射只沉积部分能量，此时测量到的沉积能量不等于散射光子的能量，这样的事件在图像重建时会增加本底噪声。为减少此噪声影响，测量时仅收集散射光子能量全沉积事件，此时经典康普顿散射角θ可表示为：

(2)

其中，mec2为电子的静止能量(511 keV)。

式(2)可确定放射源位于以x1位置为顶点、x1x2连线为中轴、顶角为θ的圆锥面上，大量符合康普顿散射条件的事件可得到很多圆锥，理论上这些圆锥的交点就是放射源所在位置。图1为康普顿成像原理示意图。

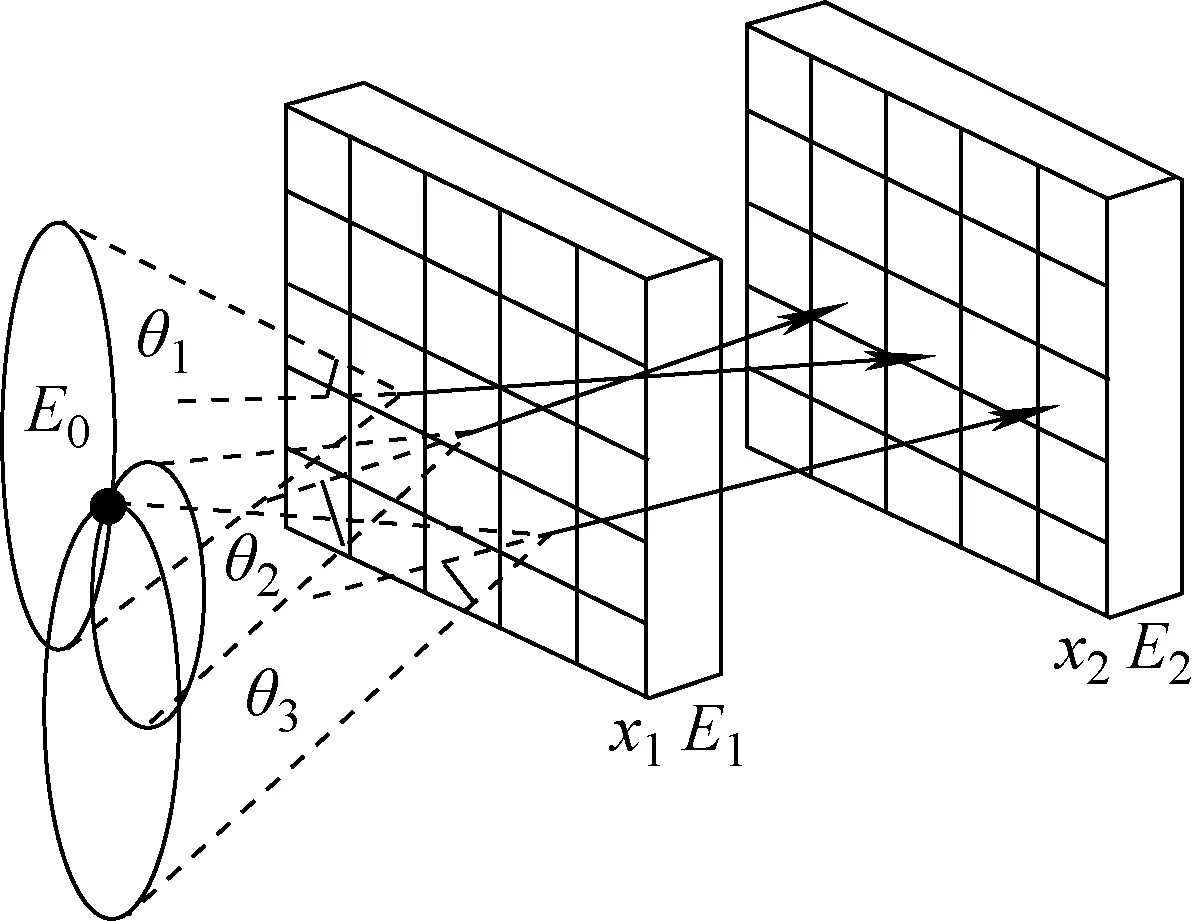
图1 康普顿成像原理示意图Fig.1 Schematic of Compton imaging principle

2 康普顿成像系统的散射角误差

康普顿成像系统角分辨本领的影响因素主要来自探测材料本身及测量系统对康普顿散射角测量时引起的角误差，其中探测材料引起的散射角误差主要源于探测材料的多普勒效应，记为ΔθD；而测量系统引起的散射角误差则主要取决于系统的能量分辨本领和位置分辨本领，分别记为Δθr和Δθg。为研究康普顿成像系统角分辨本领的影响因素，本文分别对Δθr、ΔθD、Δθg进行研究。

2.1 能量分辨本领引起的散射角误差Δθr

由于函数变量含有误差会致使函数也含有误差，该误差可用统计学中的误差传播定律进行估计，对式(2)使用误差传播定律[7]可得：

(3)

其中，ΔE0和ΔT′e分别为由测量系统能量分辨本领造成的对入射光子全能峰能量及反冲电子动能的测量误差。由于ΔE0仅来自于对测量系统的刻度偏差，通常比ΔT′e小得多，因此Δθr可表示[7]为：

(4)

2.2 多普勒展宽引起的散射角误差ΔθD

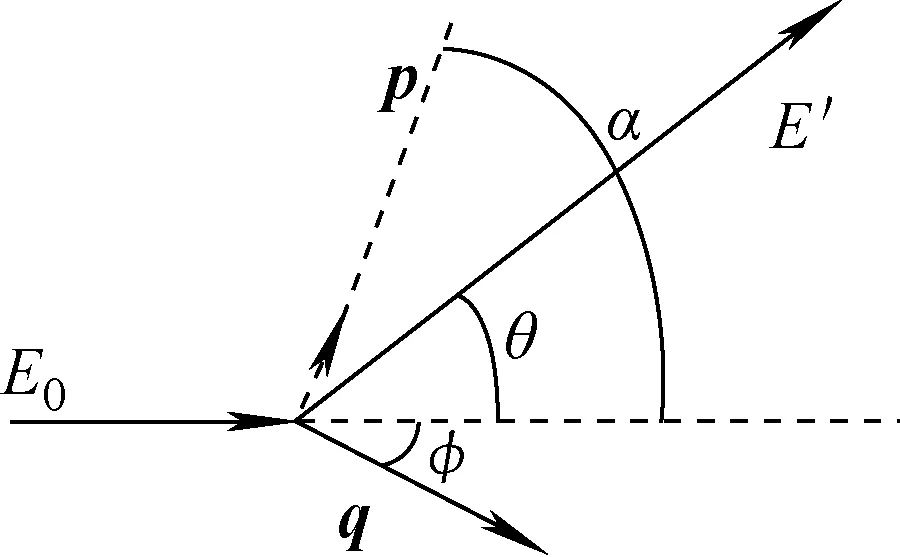
图2 康普顿散射的实际过程Fig.2 Actual process of Compton scattering

经典康普顿效应假定入射光子与探测介质原子中静止的轨道电子发生散射产生次级散射光子，但实际上介质原子中的轨道电子并非静止不动，而是以一定的动量运动，此时次级散射光子将产生多普勒展宽，该展宽将引起一定的康普顿散射角误差，进而影响系统成像效果[15]。图2为康普顿散射的实际过程，假定探测介质原子的轨道电子在某一特定的轨道上绕核子旋转，其发生康普顿效应前后轨道电子动量分别为p(与入射方向夹角为α)和q(与入射方向夹角为φ)。

若轨道电子之间的库仑力忽略不计，则吸引核子的库仑力与电子的向心力相平衡，由该平衡关系可推得：

|B|=|Te|

(5)

其中：Te为发生康普顿效应前该轨道电子的动能；B为该电子所在轨道结合能。

利用上述模型，若入射光子转移的能量足以使得电子成为自由电子(即碰撞后电子势能为0)，则根据散射过程的动量和能量守恒及狭义相对论动力学，并结合式(5)可得到以下方程组：

(6)

E0-E′=B+T′e

(7)

q2c2=T′2e+2mec2T′e

(8)

p2c2=B2+2mec2B

(9)

求解上述方程可得，当考虑介质原子中轨道电子的结合能B，且假定其具有一定初始动量p时，康普顿散射角的一般表达式为：

(10)

式(10)中的正、负号分别对应α=0°和α=180°，即轨道电子的初始运动方向正向或背离光子入射方向。由式(10)可得出对于任一给定能量的反冲轨道电子，由多普勒效应引起的平均散射角误差ΔθD为：

(11)

其中，θα=180°和θα=0°分别对应介质原子中轨道电子的初始运动方向背离和正向光子入射方向时的康普顿散射角。

2.3 位置分辨本领引起的散射角误差Δθg

受探测器位置分辨本领所限，对入射光子与探测介质原子发生相互作用位置的测量会造成散射角误差Δθg。图3为康普顿成像探测系统位置分辨本领造成角误差的示意图，其中假设探测介质网格体积等效于质心位于相互作用位置，半径等于测量误差δx的球形区域，d为入射光子在探测介质中发生两次相互作用位置之间的距离，Δθg计算公式为：

(12)

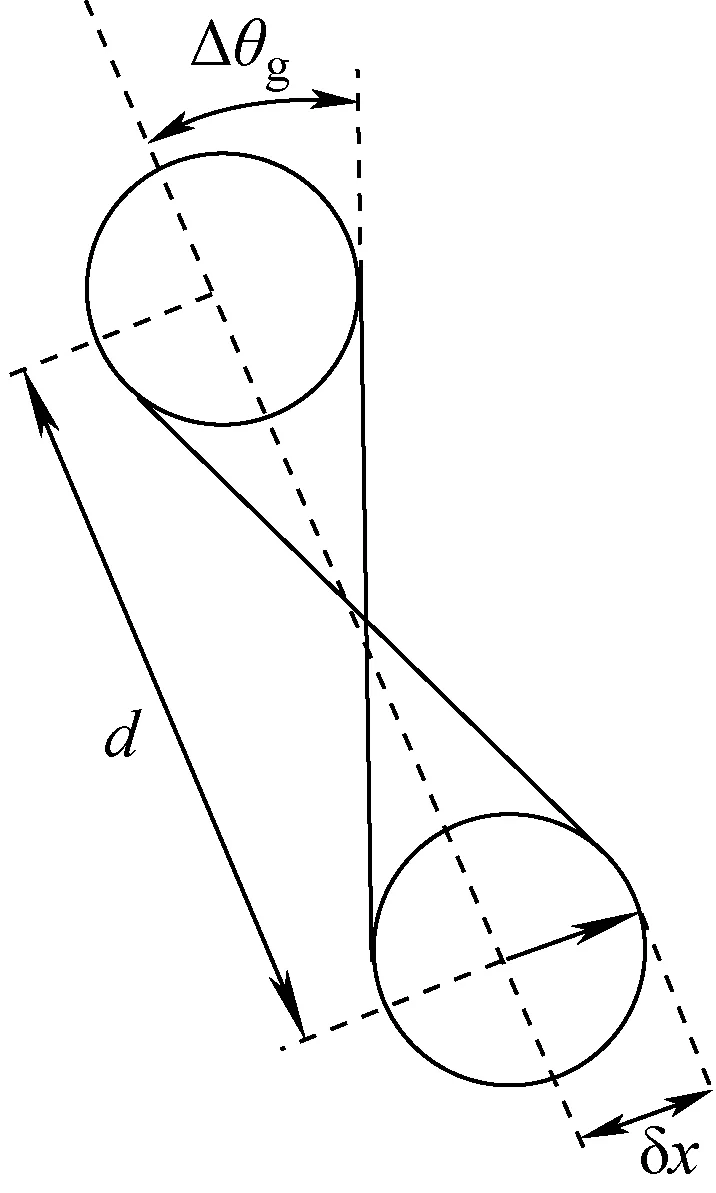
图3 康普顿成像探测系统位置分辨本领造成角误差Δθg示意图Fig.3 Δθg caused by position resolution ability of Compton imaging system

由式(12)可看出，Δθg与δx呈正比，与d呈反比，因此较小的相互作用距离会造成较大的Δθg，此时将恶化系统角分辨本领。需注意的是，成像效率也与d呈反比，较大的d虽降低了Δθg，改善了系统的角分辨本领，但同时也降低了系统的成像效率，因此成像系统设计时应根据具体情况权衡比较后确定。

3 散射角误差估算

3.1 Δθr的估算

本文建立了康普顿成像系统模型，该模型由两层25.4 mm×25.4 mm×5 mm的CZT晶体组成，层间距设置为4 cm，该晶体的能量分辨率为3%(662 keV)和5.5%(122 keV)。使用该模型计算了不同能量(122 keV、662 keV、1.33 MeV和2 MeV)光子入射后Δθr随其散射角的变化情况(图4)。由图4可看出：Δθr随入射光子能量的升高而降低，由此验证了使用CZT晶体作为探测材料的康普顿成像系统不适合低能光子成像；对给定能量的入射光子，Δθr与散射角之间呈先降低后升高的趋势，过大或过小的散射角造成的Δθr较大，此时将恶化系统的成像角分辨率，因此对中高能光子进行康普顿成像时，过大或过小的散射角应受到限制。为避免过大的散射角误差(>5°)，表1列出了本工作对662 keV、1.33 MeV和2 MeV入射光子的建议散射角范围及该范围内的Δθr。

图4 不同能量入射光子的Δθr随散射角的变化Fig.4 Δθr vs scattering angle with different energy incident photons

表1 不同能量光子入射时散射角取值范围及其对应的ΔθrTable 1 Δθr corresponding to scattering angle range of photons with different energy

本工作研究的是晶体的本征能量分辨率引起的角误差影响，未考虑后续电路的影响，合理的电子学线路设计可能会改善分辨率，则上述角误差可能会相应减小，但改善幅度有限。

3.2 ΔθD的估算

本文分别计算了不同能量(662 keV、1.33 MeV和2 MeV)光子入射CZT晶体时多普勒效应引起的散射角误差ΔθD。由于与入射光子发生碰撞的电子所在轨道未知，ΔθD不能唯一确定。为了表征实际误差，分别按照Cd、Zn和Te原子中壳层、支壳层轨道电子数占核外总电子数的比例进行加权求和来获得不同能量光子分别入射Cd、Zn和Te原子的平均散射角误差。表2列出了Cd、Zn和Te原子不同壳层、支壳层的轨道电子数和结合能。此外，为了得到CZT晶体(Cd0.9Zn0.1Te)的平均散射角误差，本工作按照该晶体中Cd、Zn和Te原子的康普顿散射宏观截面的比例进行了加权求和。图5为不同能量光子入射CZT晶体后平均散射角与反冲电子能量之间的关系。可看出，当不同能量光子入射CZT晶体时，康普顿平均散射角与反冲电子动能均呈正比。当662 keV、1.33 MeV和2 MeV光子分别入射CZT晶体时，不同散射角范围对应的ΔθD列于表3。

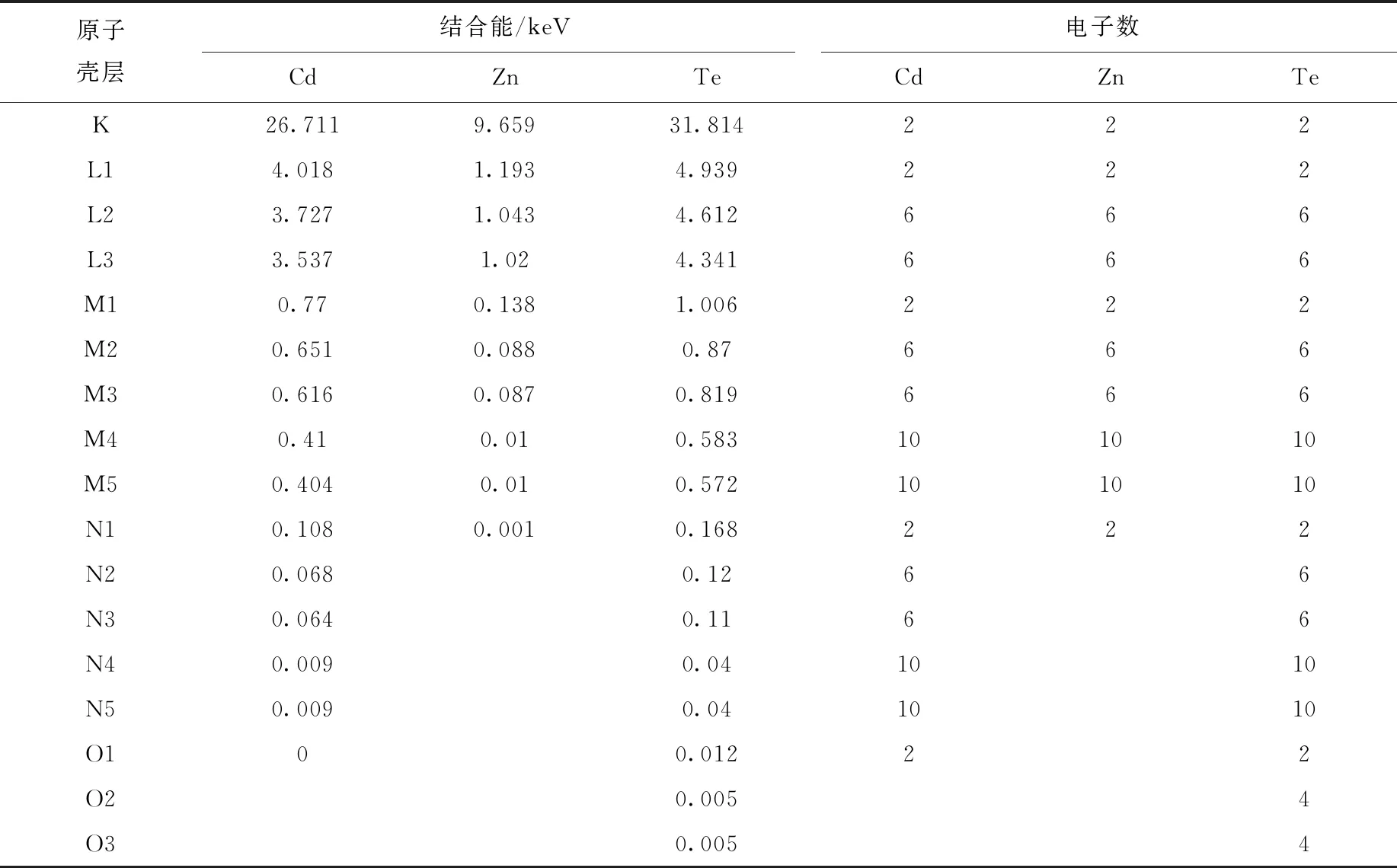
表2 Cd、Zn和Te原子壳层、支壳层的轨道电子数和结合能Table 2 Orbital electron number and binding energy for atomic shell and subshell of Cd, Zn and Te

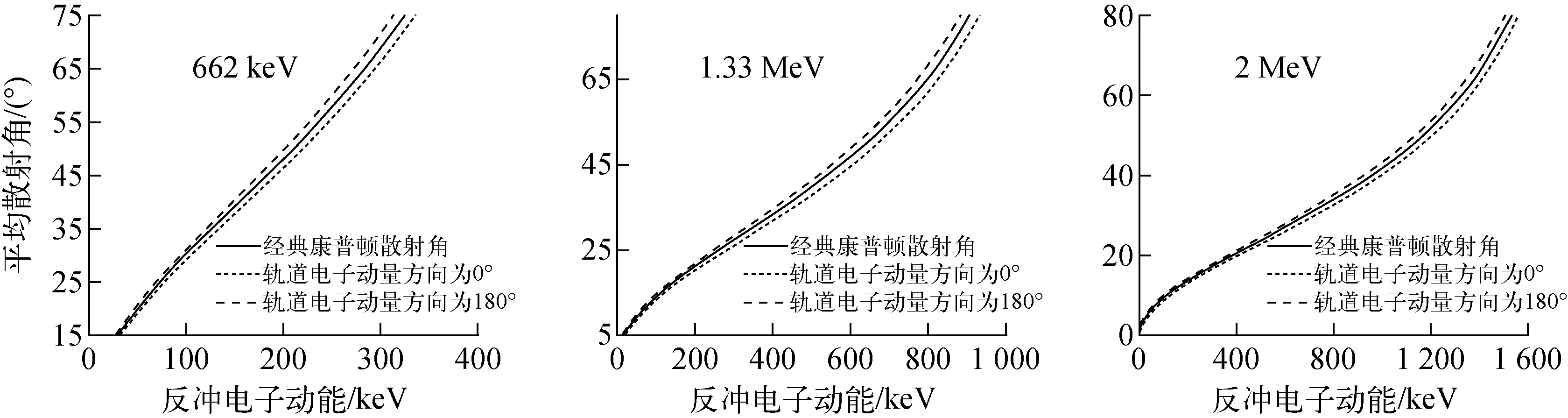
图5 不同能量光子入射CZT晶体后平均散射角与反冲电子能量之间的关系Fig.5 Relationship between average scattering angle and recoil electron energy after different energy photons incidence on CZT crystal

表3 不同能量光子入射时不同散射角范围对应的ΔθDTable 3 ΔθD corresponding to scattering angle range for different energy photons

3.3 Δθg的估算

本工作拟采用16×16路像素型CZT晶体实现成像功能，该晶体的位置分辨本领约为1.39 mm，系统信号处理时认为在每个晶体像素格内发生的相互作用位置均位于该晶格的中心。表4列出不同层间距情况下康普顿成像系统的Δθg。由表4可知，Δθg随两层CZT晶体层间距的增加而减小，为满足系统成像角分辨要求应使层间距大于3 cm为佳。

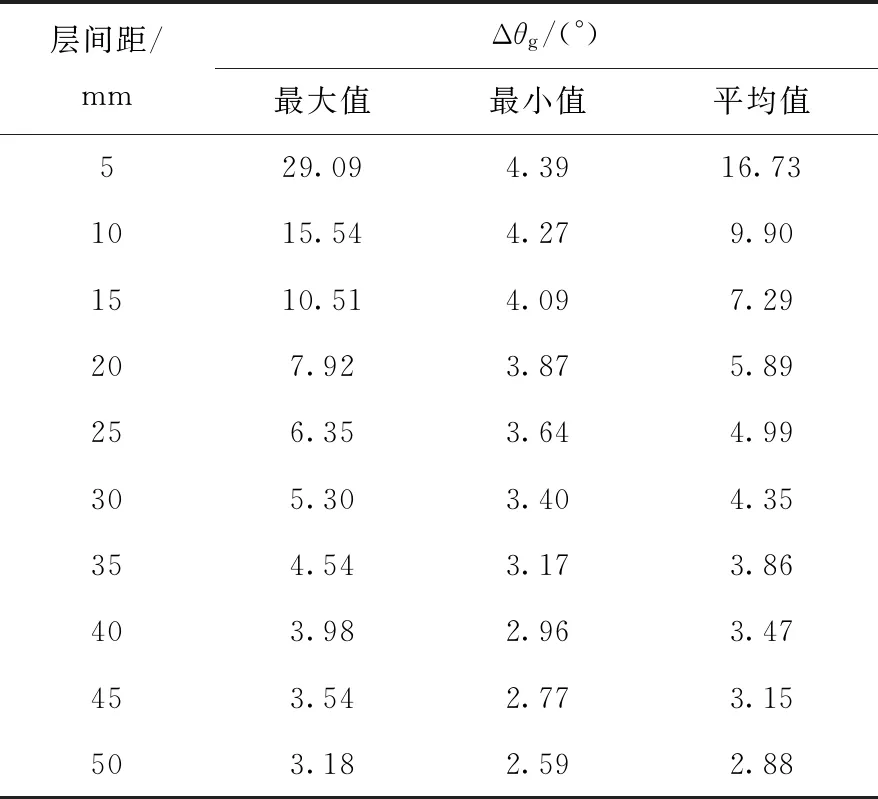
表4 不同层间距情况下康普顿成像系统的ΔθgTable 4 Δθg of Compton imaging system at different layer intervals

图6 系统成像效率模拟结果Fig.6 Simulation result of system imaging efficiency

使用Geant4建立了康普顿成像系统模型，假设不同能量(662 keV、1.33 MeV和2 MeV)光子点源位于距第1层晶体中心5 m处入射，入射粒子数为106。使用该模型对不同CZT晶体层间距下成像系统的成像效率进行模拟计算，结果如图6所示。可看出，系统的成像效率随入射粒子能量的增加而降低，同时随两层CZT晶体层间距的增加而降低。综合考虑成像系统的成像效率及角分辨要求，建议层间距取4 cm。当662 keV、1.33 MeV和2 MeV光子分别入射CZT晶体时，在不同散射角范围内Δθg及其相应成像效率列于表5。

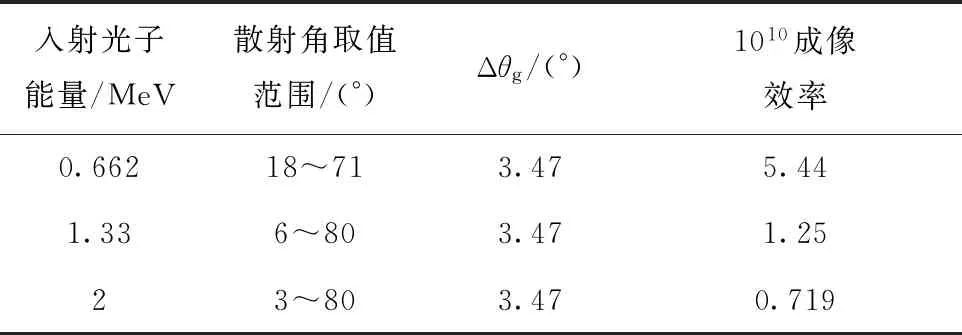
表5 不同能量光子入射时不同散射角范围对应的Δθg及成像效率Table 5 Δθg and imaging efficiency corresponding to scattering angle range for different energy photons

3.4 小结

根据误差叠加原理，总的康普顿散射角误差Δθall为：

(13)

针对所建立的康普顿成像系统，不同能量光子入射时的Δθr、ΔθD、Δθg及Δθall列于表6。

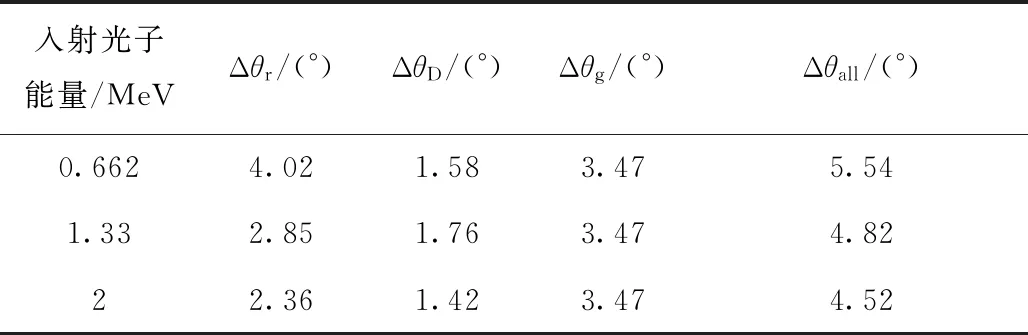
表6 不同能量光子入射时的Δθr、ΔθD、Δθg及ΔθallTable 6 Δθr, ΔθD, Δθg and Δθall for different energy photons

由表6可见，当能量为662 keV、1.33 MeV和2 MeV的光子入射时，Δθall分别为5.54°、4.82°和4.52°，且随入射粒子能量的升高而降低，其中对Δθall的主要贡献来自探测系统位置分辨本领和能量分辨本领，探测材料多普勒效应引起的角误差贡献相对较小。

4 结论

本文模拟构建了一个由位置灵敏CZT晶体组成的双层康普顿成像系统，并利用理论与模拟计算相结合的方法，对引起该成像系统散射角误差进而影响其角分辨能力的若干因素开展了理论研究，推算了不同能量光子入射时由不同角分辨影响因素引起的散射角误差范围，进而提出了对该成像系统结构的优化设计。结果表明：康普顿成像系统探测器的能量及位置分辨本领是影响该成像系统最终角分辨率的主要因素；成像数据处理时可采用适当限制康普顿散射角范围、选择有效成像事件的方法来改善成像系统角分辨能力，降低散射角误差，优化系统最终成像效果和成像效率。同时本文提供了一套对康普顿成像系统散射角误差的合理估算方法，估算得到的结果作为后续图像处理算法的必要参数，为最终系统实现成像及实验装置结构的确定奠定了基础。