中国城乡居民多代际收入流动研究
李芳芝,张焕明
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233000)
一、引言
多代际收入流动的研究源于代际收入流动,代际收入流动亦称代际收入转移,一般以相邻两代人的收入作为主要研究变量,考量一个人的收入在多大程度上由其上一代人的收入决定。Becker和Tomes提出的“效用最大化的家庭行为”理论模型为代际收入流动分析提供了基本的分析框架,他们从单个家庭的效用函数出发,分析了均衡收入不平等、代际转移、家庭和市场参数的估计、异质性家庭、政府收入再分配等,涉及不平等与代际转移的各个方面内容,推导过程也较为复杂[1-2]。Solon在此模型基础上进行了简化,提供了一个相对简单的理论模型,为代际收入流动的实证研究提供了理论指导框架[3]。此后涌现出代际收入流动的大量成果,一是围绕代际收入弹性的估算,大大丰富了代际流动的研究内容,同时为多代际收入流动的研究奠定了理论基础。
多代际收入流动涉及三代及三代以上的收入转移,Becker和Tomes早在1986年就曾对多代际收入流动问题这样描述:祖先的所有优势和劣势在三代人之后几乎全部会消失,与中国的俗语“富不过三代”的说法有异曲同工之处。但是Clark在其新书《虎子崛起:姓氏与社会流动的历史》(The Son Also Rises:Surnames and the History of Social Mobility)中,通过对全球历史数据库中的姓氏进行分析,探究人们的命运有多少取决于父母和祖父母的身份,研究发现:当代际流动不受社会结构和政府政策的影响,代际弹性系数介于0.7~0.8的区间范围,该流动特征显示子孙的社会地位经过代代转移将会流向社会的平均水平,如果代际弹性系数高达0.8,流动的过程则更慢,需要经历上百年的时间才能使得后代的社会地位高于或低于平均水平[4]。这两种不同的观点激发了国内外学者对多代际流动研究的兴趣,两代人的代际流动研究已无法揭秘这一复杂的社会问题。实际上,Long和Ferrie认为经济和社会流动研究的首要目标是探究诸如家族基因禀赋,人力资本投资和社会网络等家庭背景因素如何影响个人的教育和职业前景,用一个简单的两代际AR(1)过程来揭示这一问题是没有依据的,家庭背景因素的影响完全有可能追溯到比父代更远的年代,如果这种假定得到经验研究的验证,那些测度和比较不同国家和不同时期代际流动问题的大量文献,无疑系统性地高估了真实的代际弹性系数[5]。
多代际流动研究对数据要求较高,要求获取三代或三代以上人的纵向观测数据,这也是其研究成果的数量远远落后于两代际流动的主要原因,但是国外学者得益于长期观测数据的获取优势,仍取得了一些建设性的研究成果。社会学家Robert Hodge早在1966年曾使用美国三代人的职业分类数据研究其职业流动性,检验代际间的职业转换概率是否服从一阶马尔科夫过程,为多代际流动研究开创了新篇章[6]。此后很多社会学家对多代际职业流动和教育流动展开了大量经验研究,研究结果发现多代际流动过程不完全符合一阶马尔科夫过程,祖父代对子代的影响通过祖父代对父代的影响进行间接传递,但祖父代对子代回归系数的数值非常小并且在统计上不显著。通过将美国1910年、1920年、1940年的人口普查数据与多种调查数据进行整合,获取时间跨度为1910—2013年共四代人的样本数据,经验研究发现1920年以后的样本队列中,祖父代和曾祖父代对子代均存在不明显的多代际收入转移。然而有些学者却得出祖父代对子代收入的显著影响,如Marchon使用巴西1966年的居民抽样调查数据,发现在控制父代收入变量的条件下,祖父代收入对子代收入的回归系数显著为正,从而认为祖父代对子代收入的影响除了通过父代间接传递,还通过祖父代对子代的直接影响进行隔代传递[7];Lindahl等使用瑞士三代人的收入数据和四代人的受教育程度数据同样得出了祖父代对子代收入的回归系数显著为正的结论,并且祖父代对子代的回归系数接近父代对子代回归系数的平方,同时使用受教育程度作为收入的替代变量进行回归,也得出同样的结果[8]。由此发现有些学者的经验研究没有得出祖父代对子代的“影响”,有些学者的经验研究却验证了这一“影响”,结论不一。Zeng等基于CHIP2002农村调查数据,研究中国农村祖父代教育对子代教育的代际转移,在控制父代教育变量的条件下,发现祖父代对子代的教育代际转移是不确定的,三代同住的农村家庭中祖父代对子代教育程度的影响是显著的,数值大小与祖父代对父代的回归系数接近,尤其在受教育程度较高的祖父代群体中这种影响更明显;而对于三代不同住家庭或者祖父代已故的农村家庭,祖父代对子代受教育程度的影响微弱[9]。对于多代际流动是否存在这一问题,Mare是如此表述:多代际流动并没有统一的模式,对于其是否服从一阶马尔科夫过程也不能一概而论,在多代际流动问题的研究中,不能忽略以家庭为基础的社会不平等所产生的代际持续性这一重要根源[10]。
综合近年来学者们的理论和经验研究成果可以发现,针对多代际收入流动问题的研究尚处于起步阶段,由于数据来源和数据质量的参差不齐,祖父代及更遥远的祖先对子代的代际收入转移的研究成果数量有限,并且研究结论不管数值大小还是正负的争议亦从未间断,因此,多代际流动研究的未来仍任重道远。中国是一个拥有五千年历史文化传统的国家,四世同堂或三世同堂至今仍被人们津津乐道,现代社会中由于年轻的父母一代忙于工作,祖父母同住照顾子孙代的模式也是一种常态,子孙代的成长过程更是少不了祖父母的参与,因此,中国的当代年轻人收入不仅受到父代收入转移的影响,祖父代收入同样会通过多代际传递对其产生影响,但是由于数据限制,国内学者对中国多代际流动现象的研究罕见,中国多代际收入流动状况亟须关注,因此本文基于中国城乡居民的多代际收入流动的经验研究,检验祖父代对子代的多代际收入弹性系数的性质,具有较强的学术价值和现实意义。
二、多代际收入流动研究的理论框架
在Solon理论框架的基础上,又将代际收入弹性基础模型扩展到包含三代及三代以上的多代际收入转移模型,为多代际收入流动研究提供了理论研究框架[11-12]。
假定家庭i包含一个t-1父代和一个t代的孩子,这个家庭须将父代的终生收入yi,t-1在自身消费Ci,t-1和子代的人力资本投入Ii,t-1之间进行分配,预算约束为:
yi,t-1=Ci,t-1+Ii,t-1
(1)
假设父代不能从子代的未来收入中预支并且不把金融财产遗留给子代,子代获取的人力资本hit为
hit=θlogIi,t-1+eit
(2)
假设子代的终生收入yit为一个半对数收入方程:
logyit=μ+φhit
(3)
将式(2)代入式(3),可得:
logyit=μ+γlogIi,t-1+φeit
(4)
式(4)中γ=θφ为子代从父代获得的人力资本投资对收入的弹性系数。
同时父代在将自己的收入yi,t-1在满足自己的消费需求Ci,t-1和子代的人力资本投资Ii,t-1之间进行分配时,要满足效用最大化的C-D生产函数,即:
Ui=(1-α)logCi,t-1+αlogyit
(5)
将(1)至(4)式代入式(5),可得:
Ui=(1-α)log(yi,t-1-Ii,t-1)+αμ+
αγlogIi,t-1+αφeit
(6)
在效用最大化的家庭行为下,满足Ii,t-1的一阶偏导等于0,求解得:
(7)
为了导出子代对父代的收入弹性系数及祖父代可能的影响,将式(7)代入式(4)得:

=μ*+γlogyi,t-1+φeit
(8)
在同等条件下可以得出式(8)的滞后一阶等式,并乘以人力资本禀赋系数λ,然后与式(8)相减,化简变形可得:
logyit=(1-λ)μ*+φδ+(γ+λ)logyi,t-1-
γλlogyi,t-2+φνit
(9)
式(9)与式(8)不仅截距上有差异,而且包含了祖父代收入对子代收入的影响,为多代际收入流动研究的理论模型。 其中νit仍为随机变量。
三、数据处理和主要变量描述
(一)数据来源
多代际收入流动问题的研究涉及到至少三代人的收入及其他相关变量的数据,目前我国开展的涉及收入的调查大多只观测到当代人的收入数据,仅有中国健康与营养调查(China Health & Nutrition Survey ,简称CHNS)和中国居民收入调查(China Household Income Projects,简称CHIP)观测了三代人的收入数据,但是对于截面数据而言,虽然CHNS数据和CHIP数据能够根据家庭成员关系分离出祖父代、父代和子代三代人的收入,但是经过实际样本配对发现,能够满足三代人同时观测到收入数据的配对样本数量极少,很难同时捕捉到三代人的收入数据,样本数量不足产生的代际收入弹性的估计偏误同样不可避免;同时,三代人处于生命周期的不同年龄阶段,祖父代一般处于退休状态,父代处于职业生涯的中晚期,子代处于职业生涯的早期,个人的单年收入观测值与永久收入差异较大,从而产生较大的代际收入弹性的生命周期偏误[13]。而对于长期追踪的中国三代人不同生命周期阶段的面板数据更是难以实施。因此,较理想的做法是使用两样本两阶段最小二乘法,即从第一个样本获得父代和子代的收入,通过父代对其父亲(祖父代)职业特征的回溯,从第二个样本数据获得潜在的祖父代收入信息与其同样的变量特征。利用第二个样本,以祖父代特征作为解释变量来估计其收入,并以其最佳线性预测值作为潜在的祖父代收入,最后结合第一个样本数据中的父代和子代收入来估计多代际收入弹性。这就要求在第一个样本中包含有关于祖父代的变量特征,并且这些特征跟第二个样本中潜在的祖父代的变量特征相符。经过对比分析,CHIP数据作为专门的收入调查数据,比关注健康与营养调查的CHNS数据更符合上述要求,因此本文选择CHIP数据作为本文的数据来源。
CHIP数据为中国收入分配与劳动力市场研究领域中权威性的基础性数据资料。截至目前主要在1989年、1996年、2003年、2008年、2009年和2014年进行了六次入户调查,调查包含农村住户、农村—城镇流动人口、城镇住户等子样本,收集了1988年、1995年、2002年、2007年、2008年和2013年的收支信息以及其他家庭和个人信息,形成了CHIP1988、CHIP1995、CHIP2002、CHIP2007、CHIP2008、CHIP2013。其中CHIP2013的城镇住户调查问卷包含住户成员个人情况、住户收支、资产、债务等补充调查项目和住户其他情况三大部分,第一部分的住户成员个人情况包括所有家庭成员的性别、出生日期、就业情况、工作行业、单位类型、工资性收入总额等基本情况;第三部分的住户其他情况包含非本户住户成员的户主父母(祖父代)的出生年份、受教育程度、就业身份、单位类型、职业等基本情况,以及与户主不在一起生活的成年亲生子女(子代)的性别、出生年份、教育程度、就业身份、单位类型、职业、月收入等基本情况,虽然非本户成员的祖父代收入数据未予观测,但是可以通过两样本两阶段最小二乘估计(TS2SLS)方法估算出祖父代的收入。CHIP2013农村住户的调查问卷未包含与户主不在一起生活的成年亲生子女的基本情况,其它内容与城镇住户的调查问卷相同。
(二)数据处理
首先筛选出2013年末的就业情况为“就业”并且年收入总额大于1000元的男性户主;其次,从住户成员中分离出子代,并根据住户代码将祖父代、父代和子代三代样本进行筛选配对,最终得到城镇三代有效配对样本432个,农村三代有效配对样本1167个,作为本文的重点观测样本。由于中国三代城乡样本中只观测到父代和子代的收入,与户主不同住的祖父代在这个时期处于退休状态或职业生涯的晚期,其单年收入与持久收入的误差非常大,没有直接观测祖父代的收入。参考Haider和Solon的研究,单年收入的观测值在人的中年时期最能代表一生的永久收入,代际收入弹性的生命周期偏误最小[14]。因此获取祖父代中年时期的收入,可根据父代对祖父代特征的回溯,使用两样本两阶段最小二乘估计法估算祖父代中年时期的收入为最佳选择,据此推算出祖父代的中年时期约为20年前,本文最终选择CHIP1995的调查数据作为辅助样本来估计祖父代的收入。
对CHIP1995中的城镇祖父代样本进行筛选,同时根据城镇居民消费价格指数消除物价指数对城镇祖父代收入的影响,并对其取对数。由于1995年农村住户收支调查问卷中的个人劳动报酬收入分割成退休人员收入、从工作单位领取的固定收入的月平均额、非经常性收入、从其他途径获得的现金收入、从工作单位领取实物收入的估计额、从个体经营和私营企业中获取的个人净收入、乡村干部的工资和补贴、从家庭经营之外获得其他现金收入等8种不重叠收入,需将8种收入进行求和计算得出农村祖父代收入变量,然后再根据农村居民消费价格指数消除物价指数的影响并取对数。TS2SLS方法要求主样本和辅助样本的特征变量一致,因此估计祖父代收入的过程中需要将CHIP2013中的祖父代特征变量和CHIP1995中的特征变量进行合并处理,文化程度从低到高划分为小学以下,小学,初中,高中,中专、中技或职高,大专,大学或大学以上共七个等级;就业单位类型合并为机关事业单位,企业和其他共三个类别;职业类型分类参照《中华人民共和国职业分类大典》并结合问卷调查的选项,合并为七类:国家机关,党群组织,企事业单位负责人,专业技术人员,办事人员和有关人员,技术工人,其他。由此估算出祖父代在其职业生涯的中期以2013年不变价所得年收入总额,为下文的多代际收入流动研究提供数据支撑。
(三)主要变量描述
对子代、父代和祖父代三代人的对数收入、年龄、受教育程度等主要变量进行描述统计。由表1可以看出城镇居民的三代收入均高于农村居民,祖父代收入均值的城乡差距最大,父代次之,子代城乡收入差距最小;受教育程度虽然亦呈现出城镇普遍高于农村的现象,但是城乡差异却表现为子代最大,父代次之,祖父代差异最小的特征,教育的城乡不平等仍为亟待解决的问题;子代的平均年龄25岁左右,父代51岁,祖父代平均年龄都在70岁以上,符合人类的发展规律。
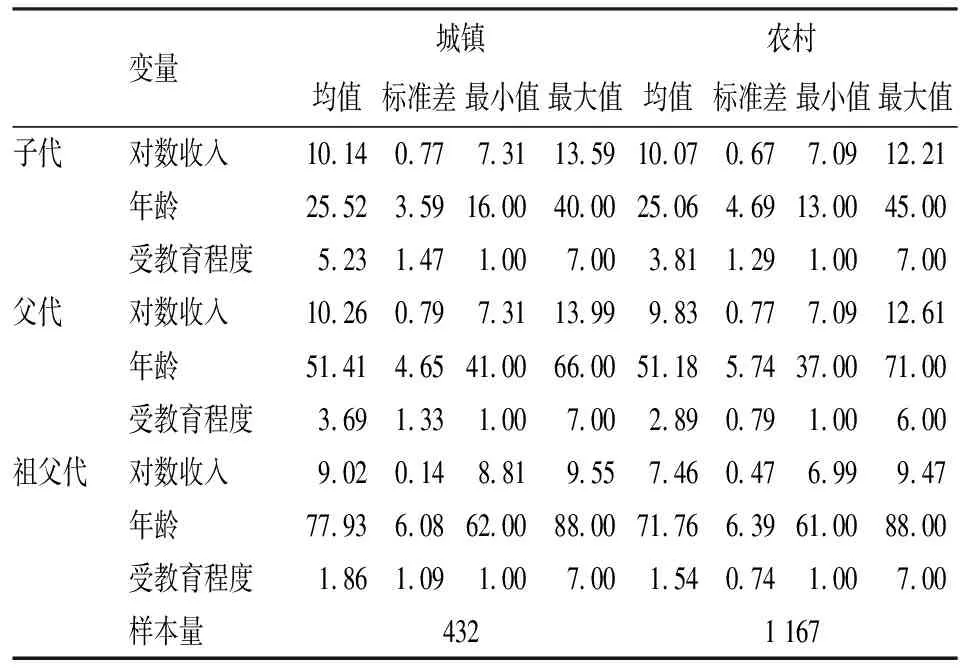
表1 主要变量描述统计
注:根据CHIP1995、CHIP2013作者整理计算得到。
四、城乡居民多代际收入流动的实证研究
(一)城乡居民多代际收入弹性的TS2SLS估计
两样本两阶段最小二乘估计(TS2SLS)实际上是一种特殊的两阶段工具变量法(TSIV),在父亲收入外生假定下得到的代际收入弹性满足估计量的一致性。特殊情况下,如果两个合并样本不是独立随机样本的情况下,TS2SLS 与 TSIV 估计得到的结果不一致。因此,为得到一致估计量,需要两个合并样本所共有的工具变量必须在两个样本中满足独立同分布。Atsushi和Solon通过比较TS2SLS与TSIV两个估计量的渐近分布,得出相比TSIV 估计量,TS2SLS 估计量更加渐近有效的结论,他们认为这是由于TS2SLS估计隐含纠正两个样本的变量分布差异,所以,多代际收入弹性的TS2SLS估计更具有理论上的优越性[15]。
基于Solon的多代际收入流动的理论模型,分别将父代收入、祖父代收入纳入模型,为了降低年龄带来的生命周期偏误,相应地控制年龄和年龄的平方项,使用TS2SLS对城乡居民的多代际收入弹性进行估计,估计结果如下表2所示。

表2 城乡居民多代际收入弹性TS2SLS估计结果
注:*、**、***分别表示在10%,5%,1%的统计水平下显著。下同。
模型I为子代对父代的代际收入弹性估计方程,城镇父子代际收入弹性系数为0.476 5,农村父子代际收入弹性系数为0.283 8,都在0.01的显著性水平下高度显著,城镇父子代际收入弹性系数比农村父子大得多,说明城镇居民的代际收入流动性低于农村。
模型II为子代对祖父代的代际收入弹性估计方程,结果显示如果只考虑祖父代收入对子代收入的影响,城镇祖父代对子代收入影响的回归系数高达0.533 3,农村仅为0.071 5,城镇祖父代收入对子代收入的影响远远高于农村,城镇子代收入的高低受祖父代收入的影响异常明显,原因可能是城镇祖父代与子代的接触更密切,对子代人力资本的投资更高。
模型III在模型II的基础上进一步控制父代收入,子代对祖父代的收入弹性下降,说明祖父代对子代的收入转移一部分通过祖父代对父代的收入转移实现,由于祖父代对子代收入的影响在理论上应该通过父代进行间接传递,导致祖父代收入的回归系数明显下降,验证了祖父代收入与父代收入之间的一阶序列相关性;但是祖父代的回归系数仍然为正,说明祖父代不仅通过基因禀赋、资本投资等实现祖父代到父代的代际转移,还通过祖父代对子代的直接影响进行隔代传递。模型III城镇父代对子代收入影响的弹性系数为0.460 3,祖父代对子代收入影响的弹性系数为0.169 3,接近父子代际收入弹性的平方,这与Marchon和Lindahl的估计结果基本一致,说明城镇祖父代除了通过父代的基因禀赋对子代进行间接收入传递,还通过对子代的直接禀赋传递以及子代成长过程的直接投资,对子代收入产生直接影响,但是这一回归结果不显著。农村子代对父代的代际收入弹性系数为0.281 7,对祖父代的弹性系数为0.048 7,略低于父子代际收入弹性的平方,在10%的显著性水平上显著,说明农村祖父代对子代收入的传递路径与城镇类似,中国隔代亲的现象在城镇和农村普遍存在。
(二)城乡居民多代际收入弹性的分位回归估计
使用TS2SLS方法得出的代际收入弹性虽然能从总体上把握多代际收入转移程度,但是对于收入分布不同位置的多代际收入转移程度缺乏认识,为了进一步计算出收入分布不同分位数上的代际收入弹性,将子代收入对父代和祖父代收入进行分位数回归。
分位数回归结果(表3)显示,城镇父代收入的回归系数呈现逐步下降的趋势,说明城镇父子代际收入流动性从低收入家庭到高收入家庭逐渐增强。城镇祖父代对子代的多代际收入弹性却在波动中上升,在0.3~0.5分位点的弹性系数都为负,祖父代对子代收入的影响为负,说明中等收入家庭中的三代最有出现逆袭或衰落的可能,城镇家庭的三代得益于城镇教育资源的优势,通过父代的人力资本投资和自己的努力跻身较高收入阶层的可能性较高,但是子代可能向上流动,亦有可能向下流动,却都不具有统计显著性。对于中高收入家庭和高收入家庭的子代,他们受祖父代的影响远远高于其他收入阶层,祖父代对子代的代际收入弹性系数高于父子代际收入弹性系数的平方,反应出高收入家庭的祖父代更注重对子代的培养和投资,隔代亲现象明显。
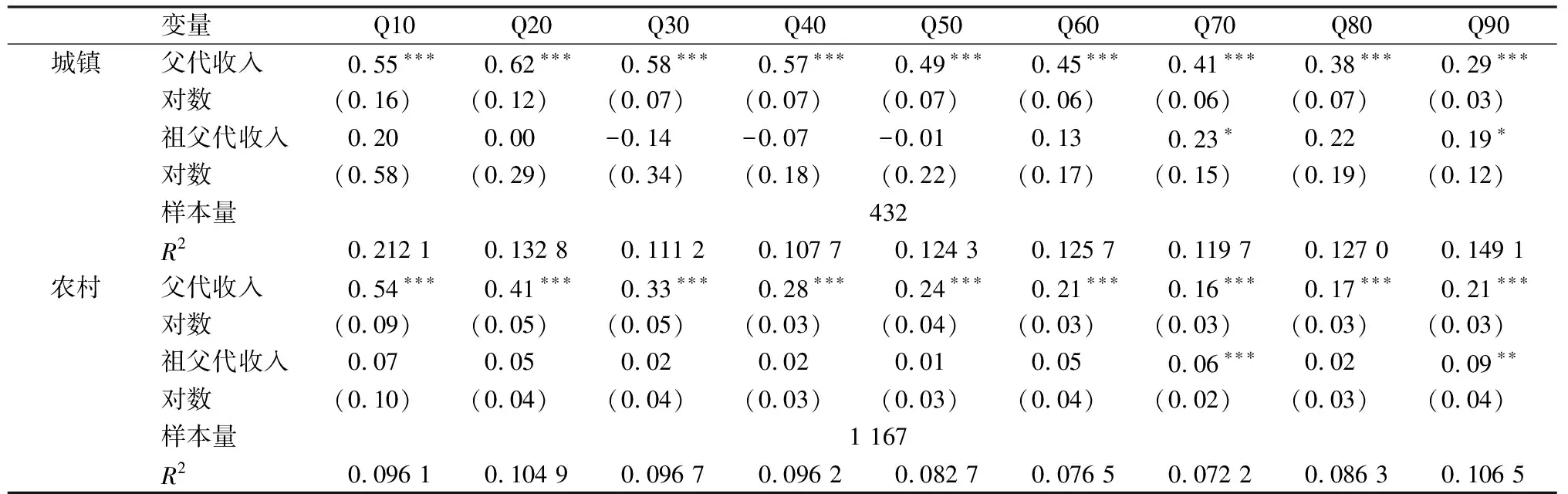
表3 城乡居民多代际收入弹性分位数回归结果
由图1和图2所示,农村父代对子代的收入弹性系数与城镇变化趋势大体一致,在收入分布的低端代际收入流动性较低,与曹俊文,刘志红(2018)使用代际转移矩阵方法的研究结果一致[15],只是代际收入弹性系数的下降幅度比城镇更快一些,收入越高的家庭代际收入转移程度越低,流动性越高,但弹性系数的数值大小整体上普遍低于城镇父子。祖父代对子代的收入弹性系数数值为正,不同分位点的变化不大,但整体数值都较小,除了0.7和0.9分位点分别在1%和5%显著性水平上显著,其他分布位置不显著,说明农村祖父代对子代收入的影响远远低于城镇,这从城镇祖父代比农村祖父代更多地参与子孙辈的抚养和投资。

图1 城镇居民多代际收入弹性变化趋势

图2 农村居民多代际收入弹性变化趋势
综合中国城镇和农村居民的多代际收入流动的回归结果可以发现,城镇和农村较高收入家庭的多代际收入转移现象更为明显,多数农村家庭和城镇低收入家庭多代际收入转移现象不明显,而城镇中等收入阶层最有可能脱离祖父代阶层,实现人生的逆袭,但是回归结果不具有统计显著性。由此我们认为,较富裕阶层祖父代对子代的回归系数为正,数值较大,并且经验研究的估计结果具有统计显著性,因此较富裕阶层多代际收入流动性不足,中国高收入阶层固化现象仍旧存在。
五、稳健性检验
不管是代际收入弹性估计的基准方程还是多代际流动的理论模型,各代的收入都是模型的关键变量,经典假设下的代际收入弹性估计要求观测到终生收入,但是终生收入的获取一直是代际流动研究的一大难题,尽管使用中年时期的收入代替终生收入会使得偏误较小,但仍不可避免。学者们解决这一难题的方法主要有三种:一是使用多年收入的均值作为终生收入的代理变量;二是使用两样本两阶段最小二乘法(TS2SLS)估计父代的终生收入;三是估算和纠正测量误差。本文对祖父代收入的估计使用第二种两样本两阶段最小二乘估计以降低临时性收入冲击的影响,为了检验上文估计结果的稳健性,对父代收入选择替代变量。CHIP2013除了观测父代当年的收入总额,还分别观测了2013年、2012年、2011年的住户可支配收入,根据式(1)的预算约束,不管一个家庭是否满足假设中的一个父代和一个子代,住户可支配收入指标比其他收入指标更能从经济学角度衡量一个家庭的收入水平和投资决策,住户可支配收入水平高,用于子代的人力资本投资相对更高,并且一个家庭的可支配收入水平主要由父代收入决定,两个变量之间的相关系数高达0.97,因此选择住户可支配收入作为父代收入的替代变量,本文使用多年住户可支配收入的均值代替父代的终生收入。因此,本文接下来使用父代中年时期的住户可支配收入均值作为父代终生收入的替代变量对多代际收入弹性进行再估计以验证估计结果的稳健性。由于在整理父代可支配收入均值数据时筛选掉个别缺失样本,故样本量略有减少。
通过两样本两阶段最小二乘估计(TS2SLS)发现城镇和农村居民的多代际收入弹性的估计结果(见表4)与表2的结果非常接近,说明上文使用中年时期父代的收入水平代替其终生收入进行多代际收入弹性的估计结果具有一定的可靠性和稳健性。

表4 城乡居民多代际收入弹性估计的稳健性检验
使用住户可支配收入均值替代父代终生收入的分位数回归结果的趋势图(具体估计结果由于篇幅限制予以省略)如图3、图4所示,农村多代际收入弹性的估计结果与表3基本一致;城镇父代和祖父代收入弹性系数在0.1到0.9分位点的数值虽然个别发生了变化,如城镇祖父代收入的弹性系数在0.1分位点由正变为负,在0.2分位点又增大到0.18,但是0.3到0.5分位点的弹性系数依然为负,说明城镇中等以下收入家庭子代受祖父代收入的影响微弱,但是得益于城镇更优越的教育资源和就业环境,他们脱离祖父代收入阶层的可能性更大;城镇中等偏上收入阶层和高收入阶层祖父代收入弹性系数依然都较高,并且高于父子代际收入弹性系数的平方,说明城镇中高收入祖父代对子代进行隔代投资和禀赋遗传的现象明显。

图3 城镇居民多代际收入弹性稳健性检验
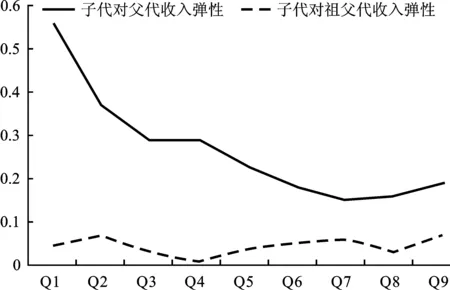
图4 农村居民多代际收入弹性稳健性检验
六、结论和展望
依据多代际收入流动的理论研究框架,本文基于CHIP2013和CHIP1995的调查数据,分别使用两样本两阶段最小二乘估计(TS2SLS)和分位数回归方法,估计城乡子代对祖父代和父代的多代际收入弹性,对中国城乡居民的多代际收入流动状况进行经验研究并进行稳健性检验,得出以下主要研究结论:(1)TS2SLS估计结果发现,城镇父子代际收入弹性大于农村父子,并且城镇祖父代收入对子代收入的影响亦远远高于农村,城镇居民的代际收入流动性低于农村居民;(2)在多代际收入流动的理论模型中控制父代收入,发现城镇和农村祖父代对子代收入的回归系数都明显下降,说明祖父代对子代的收入转移一部分通过父代间接转移实现;(3)分位回归估计结果显示城镇和农村居民的父子代际收入弹性从低收入家庭到高收入家庭都呈现递减的特征,代际收入流动性趋势反之;(4)城镇和农村低收入家庭多代际收入传递现象不显著,而城镇中等收入阶层最有可能脱离祖父代收入阶层,实现人生的逆袭,但是这一结论不具有统计显著性;城镇和农村较高收入家庭的多代际收入弹性系数为正,数值较大,尤其是城镇中高收入祖父代对子代进行隔代投资和禀赋遗传的现象明显,中国高收入阶层固化现象仍旧存在。
多代际收入流动问题既涉及到祖父代对父代,又涉及祖父代对子代的收入转移,祖父代对子代的收入转移有多少是通过父代进行间接传递,有多少是通过子代进行直接传递,以及祖父代对子代收入传递的路径等问题值得进一步研究和探索,从而丰富多代际流动的研究内容。
——基于人力资本传递机制
——基于子女数量基本确定的情形

