基于房地产市场泡沫测算的居民杠杆风险研究
李 程,杨皓熙,禹路瑶
(1.天津工业大学 经济与管理学院,天津 300387;2.北京一方商业保理有限公司,北京 100020)
一、引言
(一)研究背景
1998年的房地产改革,奠定了房地产市场成为中国支柱产业的根基。自2009年以来,在经济增长的需求与政府推出一系列利好政策的背景下,中国房地产价格开始阶段性上涨。伴随着居民杠杆率的提高,房地产泡沫和居民杠杆率阈值成为人们关注的焦点。日本房地产泡沫的破灭带来的经济衰退和美国的次贷危机都说明防范泡沫破灭风险的重要性,因此,中国一直将抑制房地产泡沫作为经济政策目标。但近十年里,中国房价总体呈现上涨趋势,其特征又呈地域分布,以北京为首的一线城市房价上涨尤为突出。与此同时,房地产价格的上升推高了居民杠杆率,从2007年的18.39%到2017年49.37%(数据来源于国家资产负债表研究中心),居民杠杆率上涨超过30个百分点,去杠杆成为这几年政府工作的重心。尽管中国具有高杠杆率特征的主体是非金融企业,居民部门和政府部门杠杆率较低,但居民杠杆率的不断上升也引起了很多学者的警惕。根据国外的警戒线,中国的居民杠杆率还有很大的上升空间,由此有些学者认为,现阶段去杠杆的主要手段在于居民部门加杠杆从而转移企业部门的杠杆率水平。但是,田国强等(2018)发布了研究报告,认为根据“居民债务/可支配收入”的算法,中国的居民杠杆率已经很高,很多家庭处于入不敷出的状态。我们应该考虑,目前的居民杠杆率到底高不高,上升空间还有多大?房地产价格是居民杠杆率的决定性因素。房价越高,居民负债就会越多,杠杆率也就越高,因此可以从房地产价格入手来研究中国的居民杠杆率阈值问题。
(二)文献综述
房地产泡沫一直是研究的热门对象,目前来说,研究方法主要有模型法、实证分析的统计方法以及指标法[1]。
指标法是当前测度中国房地产最主流的方法。一般是选取与房地产发展相关的生产、交易、金融等方面的指标,比如:房价收入比、房地产投资增长率、房价租金比等。而且,一般是通过主观判断,采用均值、临界值等作为公众对房地产价格承受能力的指标,在这些指标中,房价收入比运用最为广泛。Renaud研究发现一国房价收入比的合理区间在2~6之间[2]。进而Angel和Mayo验证了房价收入比作为衡量不动产价格的有效性,认为其是最好的指标[3]。吕江林认为房价收入比的过高将导致公众贷款买房却无力按规定还款的现象,即出现较大的房地产泡沫,从而引发银行危机,同时他指出中国房价收入比的合理上限约在4.38~6.78倍之间,与美国学者的研究基本契合[4]。
另外,关于杠杆率阈值的测算,一般用“私人部门信贷/GDP”代表宏观金融杠杆率,认为在这个比率在某个临界点前后,金融杠杆率的上升对经济增长的作用从拉动变为拖累,存在“倒U型”的关系,主要运用门限模型测算阈值[5-8],他们的研究得出了不同的门槛值。Cecchetti等认为,政府、企业和住户部门对应的杠杆率警戒线分别是85%、90%和85%[9]。
张睿锋等基于Allen和Gale信贷模型建立了加入杠杆率的拓展模型,分析了杠杆率与房地产泡沫的正相关关系[10-11]。陈宝强引入财富增长,建立均衡杠杆率模型[12]。冯文芳等研究表明,金融杠杆率与房地产泡沫之间存在双向引导关系[13]。刘晓星和石广平研究了杠杆率对资产价格泡沫影响的非线性和非对称效应,认为应该区分泡沫程度,维持合理杠杆率水平[14]。刘哲希和李子昂构建了一般均衡模型,认为居民部门不应加杠杆[15]。
总体而言,杠杆率与泡沫关系的研究主要集中在对宏观数据的整体分析,以及建立数学模型进行抽象分析,但是缺乏基于房地产泡沫测算的杠杆率阈值的具体参考值研究。
二、居民杠杆率和房地产泡沫的理论模型
居民杠杆率的选择是以居民财富值最大化为目标的,因此本文首先构建杠杆率与财富值的关系模型。
模型假设如下:
(1)存在两个时期,时期1和时期2;居民的财富包括两种资产,即无风险资产(如现金)和风险资产(如房地产),时期1无风险资产的价格为Ps,风险资产的价格为P;
(2)居民和银行签订简单的债务契约,可以从银行借款并将资金配置于无风险资产和风险资产,借款为自有资金W的一定比例,比例为b,借款利率为r;
(3)无风险资产的收益率为r*,均衡条件下r*=r>0;
(4)时期2风险资产的价格不确定,价格上升至P1的概率为α,价格下降至P2的概率为β,其中P1>P>P2,α+β=1;
(5)投资者是理性的和风险中性的;风险资产的基础价格PF是投资者利用自有资金投资于风险资产的均衡价格。
基于以上假设,风险资产的基础价值为:
(1)
投资者自有资金为W(b),是杠杆率的函数,则可借款数量为W(b)×b;投资者投资于无风险资产的预期收益为:
R=(W(b)+W(b)×b)(1+r*)-(W(b)+W(b)×b+W(b)×br)=W(b)×r
(2)
投资者投资于风险资产的预期收益为:
W(b)×b+W(b)×br)]
(3)

b+W(b)×br)]-βW(b)
(4)
由假设条件:均衡条件为无风险资产的收益与风险资产的预期收益相等,可得:R=ER

(6)
风险资产在时期1的均衡价格为:
(7)
由于风险资产的价格P高于其基础价值PF,于是便产生了泡沫,泡沫为:
(8)
令泡沫为φ,则φ>0,即:
φ=P-PF=
(9)
方程(9)两边对b求导,得泡沫对杠杆率的一阶导数:
(10)
式(10)中可见,泡沫关于杠杆率的函数为单调递增的,杠杆率上升时,泡沫也增加,再次对b求导,得泡沫对杠杆率的二阶导数:
(11)
由杠杆率对泡沫的二次导数小于0可知,泡沫关于杠杆率的函数为凹函数。得到命题1。
命题1:杠杆率对泡沫的影响为正向的,但边际影响在递减。
杠杆率上升会促进泡沫增加,这显然是符合经济现实的,居民负债增加会促进房地产市场的膨胀和泡沫的扩大,这使得居民持有的风险资产值增加,会增加居民的总财富。但是不能由此推论,居民提高杠杆率会一直增加财富值,原因在于,当居民杠杆率提高时,随着负债增加,所需支付的利息也在增加,而且随着泡沫增大,如果未来某个时刻房地产泡沫破裂,房价下降,居民财富缩水的风险在不断增大,这些因素都是理性居民必然考虑的问题。因此,居民的杠杆率提高必然有个限度,居民会根据房地产价格的变化状况选择杠杆率。
居民基于财富最大化的目标选择最优杠杆率,这个最优杠杆率和房地产泡沫的变化是密切相关的,由此可以尝试根据房地产泡沫和杠杆率的关系来判断居民杠杆率的最优值。
泡沫对杠杆率的影响,由方程(9)得,杠杆率关于泡沫的隐函数为:
φ(1+r)(1+αb(φ))=αP1(1+b(φ))-(P1α+
P2β)(1+αb(φ))
(12)
方程(12)两边对φ求导,得杠杆率对泡沫的一阶导数:
(13)
由泡沫对杠杆率的一阶导数可知,杠杆率关于泡沫的函数为非线性函数。虽然暂时无法判断导数符号的变化,但可以确定泡沫对杠杆率的影响为非线性的。那么,这种非线性关系的具体形式如何判定?根据前面命题1,杠杆率对泡沫的影响虽然也是非线性,但是单调为正的,而泡沫对杠杆率的作用是否也是单调为正?式(13)的分子必然是正数,但分母不一定,很难直接判断出符号,因此采取另外一种方法来研究。
泡沫上升意味着房地产价格必然上升,但房地产价格上升并不必然意味着居民的杠杆率也上升,我们假设居民具有理性预期,当房地产价格不断上升时,居民会意识到投资房地产的风险在不断加大,可能会主动降低杠杆率,规避风险。根据前面模型的假定,价格下降至P2的概率为β,这个概率随着泡沫扩大而变化,在某种意义上可以成为居民选择杠杆率的依据。
由于假设投资者为理性人,所以有β是泡沫φ的函数,由方程(9)得β关于泡沫的隐函数为:
φ(1+r)(r+β(φ)+α(1+b+br))=αP1(1+b)(1+r)-(P1α+P2β(φ))(r+β(φ)+α(1+b+br))
(14)
对方程(14)两边对泡沫求导,得β(φ)关于泡沫φ的一阶导数为:

(15)
由β对泡沫的一阶导数小于0可知,房地产价格下降的概率关于泡沫的函数为单调递减函数。这个结果说明,房地产的泡沫越大,房价下降概率越小,或者换句话说,房价上升或者不变可能性越大。
那么是否可以认为,居民杠杆率会进一步上升呢?显然不是。居民加杠杆会加速资产泡沫的生成与破灭,房地产泡沫破裂会导致居民财富的大幅度缩水,居民的杠杆率必随之下降,但如果此时居民的购房负债已经存在,居民的财产风险会大幅度提高,因此,理性的居民为了规避风险,实现资产保值增值,会根据房地产泡沫破裂的概率来选择杠杆率。在泡沫积累到破灭的整个过程中,预期是关键因素,当公众持续预期均衡价格在当前价格之上,且对某类产品或某一行业持续进行投资时,泡沫开始形成并滋长乃至破灭。由式(15),房地产的泡沫越大,房价下降概率越小,如果居民具有理性预期,会认为以后房地产泡沫破裂和房地产价格下降的概率越大,因此,反而会减少房地产投资并降低杠杆率。借鉴凯恩斯的货币需求理论,当利率下降时,债券价格会趋于上升,人们预期以后可能下降,就会抛出债券,持有货币。人们在超过一个临界点后,对事物的变化趋势是具有反向预期的。因此,泡沫对杠杆率的影响在超过临界点后为递减的,随着泡沫扩大,人们对泡沫继续扩大的预期下降,预期泡沫的价格将会趋于下降,逐渐向其基础价值回归,从而使人们降低杠杆率。可以认为:
命题2:居民对房地产泡沫破裂的概率的预期决定了杠杆率的选择。
房地产破裂的概率一般难以准确测算,那么居民的预期如何形成,居民的杠杆率又是由什么决定的?根据前面的分析,居民负债是基于财富最大化的追求,但负债又会带来风险,因此居民杠杆率的选择就取决于财富和风险的权衡,居民的预期也形成于财富和风险的变化。
由于风险和财富的存在,根据陈宝强(2010)的财富杠杆率模型,风险是杠杆率单调递增部分的上凹函数,即杠杆率是风险单调递增部分的上凸函数,图像如下图(a)所示。结合泡沫关于杠杆率的函数图象(c),经过杠杆率的45度线转换,可得泡沫关于风险的函数图像(d)。
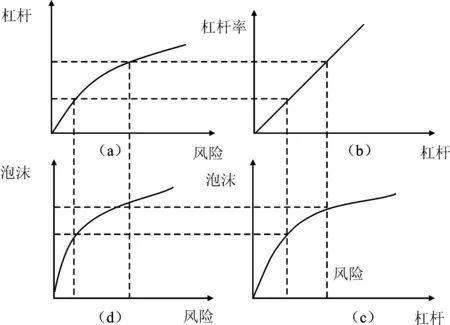
图1 泡沫对风险的影响生成图
泡沫关于风险的函数为单调递增的,但边际效应在递减,所以其反函数,即风险关于泡沫的函数为单调递增的,且边际效应在递增。其代表含义为:泡沫的扩大会加速风险的扩大。居民增加杠杆,会促进房地产市场的膨胀和泡沫的扩大,进而使得居民持有的风险资产值增加,而随和泡沫增大,泡沫破裂的概率上升,风险必然以递增的速度增加。
与此同时,财富关于泡沫的函数为单调递增部分的上凸函数,房地产价格的上升意味着泡沫的扩大,而总财富中包括风险资产的泡沫部分,因此财富随着泡沫的增加而增加,又因为随着泡沫的上升,偿债额度增加使得居民的实际收入下降,会降低居民财富增加的速度,故泡沫扩大导致的边际财富递减,见图2。

图2 泡沫对风险和财富的影响综合图
所以可得以下结论:
命题3:泡沫对风险及财富的影响均为正向的,但关于风险的边际效应在递增,关于财富的边际效应在递减。
综合心理预期和风险、财富因素的考虑,可以得出泡沫对杠杆率的作用机制。泡沫扩大后,财富和风险均在增加,开始的时候财富的增加速度大于风险的增加速度,使得居民加杠杆,而财富的增速递减,风险的增速递增,必然存在临界值,在临界值后财富的增速小于风险的增速,此时理性的居民会自动去杠杆。由此可得,杠杆率关于泡沫的函数为二次上凸函数。理性预期的居民会在泡沫增加至一定高度时降低杠杆率,减少风险资产配置,使其价格向基础价值回归;风险和财富的双重作用使得居民在泡沫持续扩大的过程中先增加杠杆,后降低杠杆率。杠杆率的临界值为b-max时,财富增长率等于风险增长率,在图2中表示为两条函数曲线斜率相等时的泡沫对应的杠杆率值。由此,本文提出命题4:
命题4:杠杆率关于泡沫的函数是非线性的,二者呈现“倒U形”的关系。
数学证明如下:当财富或者风险为0时,此时房地产市场不存在投机行为,不存在房地产泡沫,即财富与风险关于泡沫的函数过原点;又由命题3可得,风险R关于泡沫φ的函数为:
R(φ)=Aφ2+Cφ
(16)

财富W关于泡沫φ的函数为:
W(φ)=Dφ2+Eφ
(17)

杠杆率b是关于财富W的增函数,关于风险R的减函数,即:
b(W,R)=W(φ)-R(φ)
(18)
联立式(16)(17)(18),可知杠杆率关于泡沫的函数为:
b(φ)=(D-A)φ2+(E-C)φ
(19)
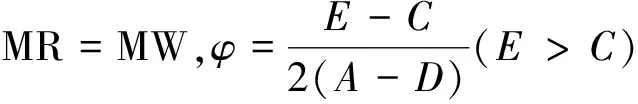
本部分的创新之处在于在Allen和Gale(2000)和陈宝强(2010)的基础上,将杠杆率、泡沫和财富结合起来,构建了基于财富最大化的杠杆率与泡沫关系模型,认为居民如果具有理性预期,会主动增加和减少杠杆,增加财富并避免泡沫破裂带来的损失,根据泡沫和杠杆之间的非线性关系,理论上应该存在居民杠杆的最优值,这个值就是居民杠杆率的阈值。
总之,上述研究了房地产泡沫对居民杠杆率的影响机制,认为二者呈现“倒U型”关系,由此可以根据房地产泡沫值的变化来定量的判断居民杠杆率的阈值。理论命题需要实证来检验,下面本文基于房地产泡沫的测算来研究居民杠杆率阈值问题。
三、中国房地产市场泡沫测度
实证中对于泡沫的计算是很重要的。本文认为用房价收入比超过居民支付承受能力的临界值来测算房地产泡沫更为合适。原因在于,理性的居民是根据负债难以承受的程度和对房地产价格的预期,来选择杠杆率水平,而承受的程度和预期又取决于房地产泡沫,由此,房地产泡沫的大小成为决定居民杠杆率阈值的基础。
(一)房地产泡沫及其发生临界值的计算方法
房地产泡沫可以定义为对其真实价值的偏差程度,即房地产价格分为真实价值部分和泡沫价值部分。近二十年来,中国房价急剧增长,国内经济学者们乃至中央政府都给予了高度的重视。但房价的急剧上升,并不意味资产泡沫出现的必然,也更不是房价估值过高而至破灭的条件。因此,合理的计算房地产的基础价值尤为关键。
微观层面来说,供求关系是决定房地产基础价值的重要因素,包括建房成本c,人均可支配收入YD,利率r等等。本文借鉴袁志刚和樊潇彦对房地产理性泡沫分析文中的估算公式[16]:
计算房地产的基础价值P*,再通过公式φ=p-p*,计算出泡沫φ,其中,p表示房价,其选取是泡沫计算的关键。本文对于房地产价格没有选取现实值,而是尝试计算达到居民还款支付承受力上限的价格,这种方法计算出的泡沫能够更准确地反映出居民对杠杆率的接受程度,根据此泡沫计算的杠杆率阈值应该更加合适。
那么,该如何计算这个价格P?直接计算是较为困难的,因此,先计算出动态的房价收入比的临界值,再根据居民的收入现状,得出房地产价格的上限值。其中,房价收入比的临界值也就是房地产泡沫发生的临界值,可以通过对房价收入比临界值的测算间接判断房地产泡沫是否存在以及计算泡沫的大小。
借鉴杨晃和杨朝军的方法,动态房价收入比的公式如下[17]:
其中:

B——居民边际消费倾向,本文通过凯恩斯消费方程C=A+BY,并通过2003—2016年的数据进行回归,得到b为0.59%
R——住房按揭利率,采取近十年来市场住房按揭利率的平均值5.62%
K——首付比例,按30%计算
G1——前10年家庭可支配收入的实际平均增长率(按揭年限为10~20年)
G2——剩下年份的增长率,按前十年的一半计算,即为g1/2
M——第一阶段,即为10
N——第二阶段,n=m+t(0≤t≤10)
另外,房价收入比的定义是指单元住房自由市场价格的中值和居民家庭年收入的中值的比值。但由于目前中国没有中值数据,因此均用房价和收入的均值代替。假设一家有3口人,人均住房面积为40平方米,则:
家庭年收入=3×家庭年人均支配收入
房屋价格=3×人均住房面积×房屋每平方米价格
由此,确定了这些参数后,倘若房价收入比的真实值大于房价收入比的动态临界值,说明房地产价格已经超过了居民的支付承受能力,则说明房地产泡沫必然存在。
杨晃和杨朝军只计算了各个主要城市的房地产泡沫状况[17],本文借鉴他们的方法,先计算全国的房地产泡沫,后计算主要城市的泡沫水平与之比较。
(二)全国和各个主要城市房地产泡沫发生临界值


表1 全国房价收入比
由表1,中国房地产市场存在明显泡沫,在2007年第三季度达到最高峰,房价收入比为43.89,远超泡沫区间。2008年金融危机只带来了短暂冲击,房价收入比在小幅度下降后,又回弹至40左右。2010年限购令出台后,泡沫出现下降趋势,从最近两年来看,房价收入比在区间附近来回浮动,说明尽管房价仍持续上升,但房地产处在泡沫边缘地带。
中国地域辽阔,资源、政策的限制导致其发展必然存在差异。房地产的不动产性质又必然导致房地产市场存在地域差异[18]。根据地域分布的代表性及城市数据查找的局限性,本文在东部、中部和西部共选取了33个大中城市,截取2006—2016年共十年的年度数据进行分析,数据均来源于wind数据库,根据公式计算,得到各个主要城市的动态房价收入比临界值。
各城市动态房价收入比临界值有显著不同。2006—2016年北京、上海、深圳三个一线城市和厦门存在显著的房地产泡沫,但各城市在个别年份处于房地产泡沫边缘,如2006年、2014年和2015年的北京,又如2014年的上海和2007年的深圳。2006—2016年广州、天津、太原、沈阳、大连、南京、杭州、宁波、福州等均在房地产泡沫的边缘地段。其中,广州、天津、太原、杭州在2006—2013年均在泡沫区间上限边缘,且个别年份超过了区间上限,即存在明显的房地产泡沫。而在2014—2016年房地产泡沫有缩减趋势。青岛、武汉和成都前五年房价收入比在区间范围内,说明处在房地产泡沫边缘地带,而后几年不存在房地产泡沫。2006—2016年石家庄、呼和浩特、哈尔滨、合肥、南昌、济南、郑州、长沙、南宁、海口、贵阳、昆明、西安、兰州、西宁、银川和乌鲁木齐房价收入比都在区间范围以下,说明没有房地产泡沫。
从全国和各地方的泡沫比较来看,全国房价收入比的真实值和临界值都要高于各个主要城市的水平,进一步反映出中国发展的不平衡。各个主要城市尽管房价高,但由于收入较高,其房价收入比低于全国水平,中国仍有很多地区收入较低,存在收入分配不均匀现象。由此说明,以全国房价收入比来衡量的房地产泡沫更能体现中国整体居民面对的泡沫大小。因此,本文以全国的房地产泡沫状况来衡量杠杆率的阈值。
(三)依据房价收入比临界值计算的房地产泡沫
由于选用的房地产价格是居民对贷款承受能力上限的价格,又根据前面房价收入比临界值的计算和分析,本文首先通过房价收入比上限倒算出房地产价格,在剔除基础价值后,得出房地产泡沫φ。公式如下:
φ=房价收入比临界值上限×城镇家庭年人均可支配收入÷人均住房面积—住宅基础价值
其中,人均住房面积取40平方米,住宅基础价值按照前面袁志刚的公式计算得到。此时计算出的房地产泡沫反映出居民对杠杆率的承受能力,相对于运用房地产价格现实值计算的房地产泡沫,这个值更适合于居民杠杆率阈值的分析。
我们对中国2007—2017年季度数据进行计算,数据来源于wind数据库,并通过季节性调整后,得到了具体的房地产泡沫参考值。如图3,近十年里,尽管泡沫呈现小幅度的波动,但整体处于升趋势。

图3 房地产泡沫趋势图
(四)测算结果分析
第一,横向来看,一线等发达城市存在显著的房地产泡沫,其他城市或在泡沫边缘,或不存在泡沫,这些其他城市总体而言,房地产泡沫不明显。此外,尽管一些城市存在显著房地产泡沫,但个别年份却与结论相违背,原因可能在于统计误差以及该地区该年份地区政策的存在,此研究结果与吴冠岑和王沁颖(2017)基本吻合。
第二,纵向来看,房地产泡沫在2013年之前,处于加速增长的阶段。2013年之后,政府的重视加强,对房地产市场的宏观调控力度加大,房地产泡沫得到抑制。但近年来,居民杠杆率不断攀升,其中购房贷款占绝大部分比例,由此房价的持续高升造成房地产泡沫加剧的潜在风险,不容忽视。
第三,中国的地区差异和发展不平衡,使得全国的房价收入比高于各主要城市,以全国的房地产泡沫状况来计算阈值更为合理。
总之,中国房地产市场总体存在显著泡沫,且在地域分布上存在明显的差异。本文在这部分的边际贡献为,对全国动态房价收入比临界值进行了测度,以此为基础计算了具体的房地产泡沫水平,这个水平是居民进行杠杆率选择的参考值,是判断居民杠杆率阈值的泡沫值。
四、基于房地产市场泡沫的居民杠杆率阈值研究
(一)居民杠杆率现状
居民杠杆率的计算方法为居民信贷总额/GDP,其数据来源于国家资产负债表研究中心。从2007—2017年,居民杠杆率整体呈上升趋势,由18.39%上涨到49.37%,10年增长了30%,年均增幅3.5%。以“居民信贷总额/GDP”计算的居民杠杆率只能从宏观层面说明居民部门的债务水平,而用“居民信贷总额/居民可支配收入”计算的负债可支配收入比能从微观角度衡量居民的债务压力。由于可支配收入与GDP之间存在高度一致的正向变动关系,则居民杠杆率与负债可支配收入比每年的增幅程度几乎相同。因此,负债收入比在弥补了居民杠杆率缺陷的同时,也可以作为其考察的替代指标。

图4 居民杠杆率与负债收入比图
(二)数据说明与描述性统计
(三)居民杠杆率阈值测算
由理论部分命题4知,泡沫对杠杆率的影响是非线性的,且呈“倒U型”,因此建立非线性回归模型:

R2=0.921 2 (-2.99) (14.61)
对残差项进行单位根检验,其结果平稳,说明各变量之间存在协整关系。由回归结果可知,泡沫和杠杆率的关系呈现“倒U型”,通过计算得出居民杠杆率极大值为0.610 4。
进一步,进行稳健性检验。影响居民杠杆率的还有诸如利率r、个人住房公积金贷款利率r1、人均收入YD和人均消费支出consumption 等因素。对这些方程进行协整检验,认为各变量之间均存在协整关系。稳健性检验结果如下:

表2 居民杠杆率稳健性检验
注:()内为t值,*表示在10%水平上显著,**表示在5%显著,***表示在1%显著。下表同。

(四)基于“居民负债/可支配收入”的阈值测算
研究负债可支配收入比与房地产泡沫之间的关系,一方面衡量了泡沫对居民负债压力的影响,同时又能恰当的解决居民杠杆率和房地产泡沫的内生性问题。作为居民杠杆率的替代性指标,假设负债可支配收入比与房地产泡沫仍呈非线性“倒U型”关系。因此,建立非线性回归模型:

数据方面,仍选取了2007—2017年四个季度的数据进行分析。但由于可支配收入为流量数据,季节性程度较强,由其得出的“居民负债/可支配收入”值必然涉及到季节性调整的问题,此时调整后的季度数据与“居民负债/可支配收入”的年度真实数据存在一定误差。因此,我们采取了两种处理方式,第一种方式是由居民负债和可支配收入的季度数据计算出比值,再将计算出的负债可支配收入比进行季节性调整,进而回归。这种方式保证了负债可支配收入比数据的准确性,但季节性太强,调整后与其年度真实数据匹配度较弱。第二种方式是直接将负债可支配收入比的年度数据平滑成季度数据,这种方式的季度数据与年度数据匹配度高,但缺乏真实性。比较之下,本文主要说明方式一的测算,数据均来源于中国人民银行网站及wind数据库。对于方式一,经单位根检验后,所有变量均在一阶差分后平稳,说明各变量为一阶单整,我们认为经过季节性调整后的负债可支配收入比与房地产泡沫为一阶单整序列,可以进行协整检验,OLS回归结果如下:
R2=0.923 6 (-6.04) (20.53)
对残差项进行单位根检验,其结果平稳,说明各变量之间存在协整关系。由回归结果可知,房地产泡沫和负债可支配收入比的关系的确呈非线性“倒U型”,初步验证杠杆与泡沫关系的可靠性。且通过计算得出负债可支配收入比的极大值为2.544。同时,由方式一计算的负债可支配收入比呈持续上升趋势,截至2017年第四季度,负债可支配收入比为2.599,已经以微弱差距超过了阈值水平。而方式二计算得出负债可支配收入比的极大值为1.336。截至2017年第四季度,居民负债可支配收入比为1.380,略微超过了阈值水平。
进一步,对方式一进行稳健性检验,影响负债可收入比的因素与利率r、个人住房公积金贷款利率r1和人均消费支出consumption等因素有关,对这些变量进行协整检验后,结果显示各变量之间均存在协整关系。稳健性结果如下:

表3 方式一稳健性检验表

总的来看,通过上述实证分析可知,泡沫与居民杠杆率(或负债可支配收入比)确实呈“倒U型”关系,且随着泡沫的增长,公众对房地产价格上升的预期使得投机需求扩大,居民将持续投资房地产市场,居民杠杆率随之高升。当泡沫到达一个阈值之后,理性居民由于房价过高而并不再提高预期,此时为防止泡沫破灭所带来的经济损失,公众将随着泡沫的继续增长而退出房地产市场,从而居民杠杆率逐渐下降。这一阈值对应的居民杠杆率为61.05%。
截止2017年底,居民杠杆率为49.36%,与阈值61.05%只相差11.69个百分点,存在微弱的上升空间,而对于“负债/可支配收入”,其两种处理方式的结果均表明当前值超过了阈值水平,说明当前居民偿债压力已经超出了警戒线,且考虑到中国居民偿债压力已经高于金融危机前2007年美国的最高水平,中国已经处于危险边缘,由房地产市场过热引发的泡沫破灭风险逐渐转移到居民偿债压力变重甚至无法偿清的风险中,从而破坏金融稳定性,带来更大的经济危机。因此,在中国处于转型的关键时期,居民杠杆风险需引起高度重视。
五、结论与相关建议
本文基于Allen和Gale(2000)的信贷泡沫模型加入杠杆率与财富后,建立杠杆—泡沫模型,并通过对2007—2017年中国季度数据与2006—2016年33个大中城市的年度数据加以实证分析。得出如下结论:
第一,居民杠杆率阈值取决于追求财富最大化和房地产泡沫风险规避的权衡,房地产泡沫对杠杆率的影响为“倒U型”,杠杆率最大值为阈值,当杠杆率在阈值之前呈递增趋势,在阈值之后呈递减趋势;
第二,自2007年来,全国总体存在显著泡沫,近两年呈现回落趋势,具体而言,根据房价收入比测算后发现,全国的房价收入比要高于各主要城市,反映出各地区经济发展的不平衡。2006—2016年一线城市如北京、上海、深圳存在明显房地产泡沫,二、三线城市如天津、石家庄在房地产泡沫边缘或者不存在。目前来说,中国房地产泡沫没有达到峰值,总体较为稳定。
第三,经过对房地产泡沫和居民杠杆率的关系进行实证分析,计算可得居民杠杆率的阈值大致在61.05%。总体而言,尽管以“居民信贷总额/GDP”衡量的居民杠杆率仍存在微弱的上升空间,但以债务可支配收入比衡量的居民债务压力水平已经略微超过了阈值,中国居民举债的风险已经显现,由房地产泡沫破灭带来的居民信贷风险需高度重视与谨慎对待。
由此,本文给出以下建议:
第一,政府应该密切关注居民杠杆率的变化趋势,结合杠杆率警戒线实施对居民杠杆率的监管,意识到向居民部门转移杠杆率绝不是降低非金融企业高杠杆率的根本出路,谨慎运用增加居民杠杆率的政策手段,避免居民杠杆率的过快增长和居民债务的积累。不仅从债务/GDP指标,而且从债务/收入指标入手,对居民杠杆率的风险进行监控,避免只盯住债务/GDP指标导致的风险评估的片面性,提高监管的全面性和有效性。
第二,政府应采取一个更加稳定的房地产调控政策与目标,尽量减少公众对房地产市场趋势的错误预期,增加居民财富增值渠道,避免资金过多集中于房地产投资。居民债务的积累和居民的投资渠道少有关,居民目前能够投资的主要是银行存款、理财、股票、黄金等金融产品,产品数量少且收益率相对低,因此就把大量的资金配置到房地产上,导致负债增加,因此,控制好居民杠杆,不能只从房地产价格入手,而且应该加大金融市场整体的发展,从金融供给角度为居民提供更多盈利机会。
第三,政府应建立一个更加健全的关于房贷等相关方面的体制,增加金融稳定性,更好的实现有限资源的充分利用,严格房地产贷款审批,调节居民杠杆率结构,避免居民债务累积带来的金融风险。应严格审查房地产开发企业资质,有效控制住信贷资金流向房地产行业的比例,加强信贷合规管理,防止个人综合消费贷款、经营性贷款、信用卡透支等资金挪用于购房。房地产调控的总体基调不能全面放松,同时要把握好调控尺度,既要巩固前期调控成果,控制住房价增速和房价收入比,又要避免调控过度,导致泡沫破裂带来新的风险。

