权数在人口抽样调查估计中的应用研究
王小宁
(中国传媒大学 数据科学与智能媒体学院,北京 100024)
一、引言
基于人口调查的分析始终是人口学研究领域的一个关键问题,当前对人口统计相关的研究主要基于全国人口普查数据,而对此的研究也集中采用第四、五、六次人口普查的数据。人口抽样调查是根据随机原则从所研究的人口总体中抽取一部分单位作为样本,并利用抽取的样本数据去推断总体相应各项指标值的一种非全面调查。调查目的是用样本信息去推断总体信息,理想的情况是每个样本代表的信息是相同的,但大多数情况下不同样本代表的信息是有差异的。不少学者在处理抽样数据时,只是用抽样数据直接对总体进行估计,而不去考虑样本的代表性问题,从而造成一定的偏差,使得样本数据代表总体信息的说服力下降,本文基于此种现状提出一种基于权数的参数估计和控制方法。
本文旨在分析常规的人口抽样调查中计算权数的一般步骤和权数调整及控制方法,并结合刀切法计算参数的标准误差,将权数调整和权重控制方法同时加入到常规的加权估计中,一方面有效控制了估计的标准误差,另一方面降低了变量的变异系数。同时,采用第四次中国城乡老年人生活状况的调查数据(1)第四次中国城乡老年人生活状况抽样调查数据来源于http://dscdc.cncaprc.gov.cn,由中国老龄科学研究中心提供。(以下简称老年人调查)为例进行分析,证明加权调整方法的实用性和有效性。
权数就是一种表征样本代表总体的指标,可表示为衡量被抽中的个体所能代表的抽样群体的人口数量。广义的权数是指以某种数量形式来测度被评价事物中各因素自身相对重要程度的度量值。权数是指以某种数量形式对比、权衡被评价事物总体中诸因素相对重要程度的量值,它集中反映了统计总体中各个指标的重要程度。在抽样中,权数反映每个最终样本单元对总体单元代表性的程度,其在调查数据的统计推断中,占有重要的地位。在人口抽样调查中,权数表示被抽中的样本在还原总体的过程中所代表的人口数。权数的作用主要体现在两方面:一方面,通过权数能够将样本还原到总体,反映不同单元在总体特征估计中的重要程度,获得总体特征的无偏估计;另一方面,由于抽样的随机性以及在实施过程中出现的无回答等情况,会使得样本单元结构和总体结构之间不一致,这种不一致将会直接影响到统计推断的精度,因此在实际使用权数过程中,需要对权数进行适当调整,以使得样本单元的结构和总体的结构接近,方便进行参数估计等深入的分析。
利用人口普查数据和抽样调查数据,不少研究者得出了很多有意义的结论,同时也发现了普查的一些问题,例如吴连霞和吴开亚采用全国第四、五、六次人口普查数据探析1990—2010 年中国人口老龄化时空演变规律,利用动态年龄指标,通过构建生命表测度老年人口与老龄化,运用GIS空间分析法与固定年龄测算的老龄化进行比较分析,厘清了悲观老龄化的认识误区,对拓展老年与老龄化研究方法和老龄社会的应对策略等均具有一定的理论价值和现实意义[1]。张耀军等根据北京市第三、四、五、六次人口普查的数据,借助ArcGIS空间统计分析工具和技术对北京市人口空间分布进行了一定的分析并对优化北京人口空间提出了一些建议措施[2]。但是,普查数据也有一定的质量问题,张为民分析了2000年人口普查数据,得出中国人口统计的数据质量呈下降态势,人口漏报达到1.81%,同时分析了产生漏报的原因是既有普查方案设计的影响,也与群众配合、经费投入、行政考核等密切相关,并对第六次全国人口普查提出了具体的解决方案[3]。胡桂华和薛婷针对当今民事登记系统覆盖评估领域存在利用辅助信息量有限而难以提供精度高的净误差率的不足,提出用三系统估计量替代独立双系统估计量[4]。胡桂华的研究结论表明,真正的人口普查误差其实是不能计算的;基于罗吉斯蒂回归模型的双系统估计量由于不受样本量限制而可以选择较多的事后分层变量,优于基于事后分层的双系统估计量[5]。
针对权数的分析,不少研究者从不同角度分析了其重要作用,金勇进和张喆系统阐述了抽样调查分析中权数的获取和调整过程,同时提出了一种利用权效应来对权数进行评估的方法[6]。罗薇从不均等选择概率的角度,提出两类常见的权数调整类型及其调整方法——规模调整和结构调整应用于复杂样本设计[7]。金勇进和刘展对非概率加权抽样推断提出了一种新的方案,即先采用倾向得分匹配选择样本,再用倾向得分逆加权、加权组调整和事后分层调整对匹配后的样本进行加权调整来估计目标总体[8]。针对抽样调查中的无回答问题,贺飞燕认为,加权过程中对不同的无回答调整阶段反映出的数据收集方法存在问题,并提出了具体建议[9]。
二、权数基本理论
具体调查实践中,权数的计算过程包含了两个方面:设计权数和实际权数的计算,权数调整以及误差计算。设计权数的计算是基于问卷设计方案计算出来的权数,而实际权数是基于获取的样本信息得到的权数。本文以老年人调查为例进行详细的分析,此次调查设计遵循科学性、高效性和可操作性原则。首先,此次抽样方案设计是严格的概率抽样,抽取样本用以满足全国目标量估计的需求。其次,抽样设计保证有较高的效率,即在一定的抽样误差范围和调查经费内保证较高的估计精度。最后,抽样设计结合了中国的实际情况,具有较强的可操作性。
(一)权数计算
设计权数是特定抽样设计下,各样本单元包含概率的倒数,不同包含概率的样本单元的权数也是不一样的。对于多阶段抽样,设计权数为各阶段样本单元包含概率的倒数的乘积。由于抽样调查数据辅助信息所限,无法获得各街道(乡镇)、各居(村)委会的老年人口总数,故无法计算第三、四阶段的样本单元入样概率,因此设计权数的计算公式较一般的多阶段抽样而言有所简化。
以此次老年人抽样调查为例,第h个省份的第i个区县第j个街道办事处或乡镇,第k个居(村)委会第l个被抽中的老年人的设计权数公式如下:

(1)

设计权数是在保证抽样过程中完全按照设计方案得到的样本权数,但是在实际的调查过程中,往往存在无回答或其他突发情况导致调查样本比设计的多或少,样本结构和实际人口结构不一致的情况,这就需要对设计权数进行进一步的调整,从而计算出基于实际调查样本的实际权数。实际权数,主要是通过对实际调查样本单元的无回答、无覆盖进行的计算调整,是实际的抽样调查中获取的权数,实际权数有利于获取调查样本的代表性信息,实际权数的计算包含无回答调整和结构调整。
需要说明的是,在整理问卷的过程中,往往存在因回答不符合要求被判为废卷等情况,这是在数据处理阶段要解决的事情,权数计算和调整只是利用清理完成的数据进行计算,对于问卷中的项目无回答情况,一般采用插补的方法进行解决[10]。
(二)无回答调整
无回答调整涉及各个阶段的无回答调整,包括省份无回答、区县无回答、街道(乡镇)无回答和居(村)委会无回答等,但由于在实际的调查过程中一般前三个阶段无回答情况较少,因此以居(村)委会的无回答调整为例进行说明。由于没有抽样的名单,只有实际调查的数据,所以无回答调整仅就居(村)委会层面进行无回答调整。无回答调整得到的权数是各个居(村)委会拟抽人数nhijkl除以实际调查的人数L再乘以设计权数,调整后的权数为:
(2)
(三)权数的结构调整
权数是样本单元实际代表的未入样单元个数,其主要功能就是将样本单元还原到总体。然而,由于样本抽取的随机性,可能造成样本单元的结构分布与总体结构不一致,导致推断的精度降低。因此,还需要对实际权数进行结构调整,使得样本单元的结构与总体一致。
常见的结构调整方法有:校准加权法、迭代法、事后分层法。金勇进和张喆对几种方法进行了详细的说明论证[6]。根据本次调查的实际情况,本次权数调整使用迭代法,以省为分层变量,在各个层内分别进行权数的结构调整。
在结构调整中不仅要考虑样本单元的年龄结构与总体一致,同时考虑性别比例与总体一致。本次结构调整只针对性别、年龄完整的样本单元进行权数的结构调整,对于性别或年龄缺失的样本单元,直接使用其经无回答调整后的权数结果。迭代调整系数为:
adjhs=
(3)
其中s表示性别或年龄。以安徽省为例,根据老年人调查数据作为样本数据和第六次人口普查数据作为总体数据进行对比,发现样本中70岁以下的男女比例比总体比例偏低,而样本中70岁以上男女比例比总体比例要高,也就是说样本中年龄结构偏大,与总体男女比例有一定的差异。这主要是由于:一是实际调查数据存在性别、年龄缺失的情况,对于这部分数据无法进行权数调整,故在此处未放入计算;二是由于使用的人口总体数据是2010年进行的全国第六次人口普查数据,而实际老年人调查是在2015年,两者本身就有一定的时间差异,因此有必要对样本结构进行调整使其与总体结构相一致。
结合式(2)和式(3),经过结构调整后的样本结构和总体结构的比例倾向一致,这样在进行深入分析时用调整后的权数就更具代表性了。经过结构调整后的调整系数如表1所示。
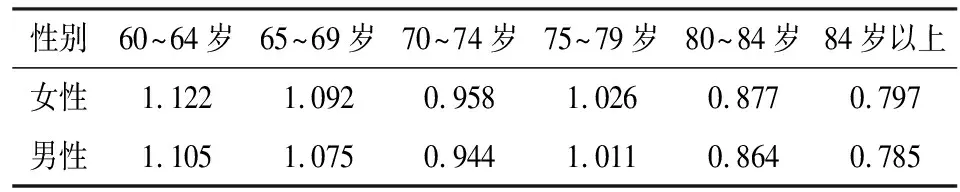
表1 安徽省的权数结构调整系数
迭代调整系数是根据样本中老年人口的性别年龄和总体中老年人口的差异,通过迭代调整得到的,可以用无回答调整后的权数与迭代调整系数相乘得到最终的权数,通过调整系数可以保证样本单元还原到总体的结构与总体大致保持一致。
(四)最终权数

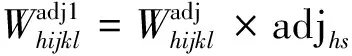
(4)
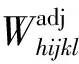
由于调查过程的复杂性,加上调查中存在的无回答、样本结构与总体结构不一致等情况,最终计算得到的权数往往差距很大,使得估计量的方差也随之变大,因此有必要对权数进行适当的控制以保证估计的方差不会太大。在抽样调查中,一般用设计效应来度量复杂抽样设计相对于简单随机抽样的效率或相对精确程度[11]。设计效应是复杂抽样设计与具有相同样本量的简单随机抽样设计的估计量的方差之比。当设计效应大于1,代表该抽样设计的变异性大,需要更大的样本量才能达到简单随机抽样的效率;反之若小于1,说明只需要少量的样本量就能达到简单随机抽样的效率。借此方法,金勇进和张喆提出了利用权效应来评估复杂抽样设计相对于简单随机抽样的权数效率或相对精确程度[6]。权效应是由抽样设计的样本权数和相同样本量的简单随机抽样设计的样本权数相比得到。一般情况下,权效应大于1,越大表示权数变异越大,需要进行一定的控制,使其在一个合理的范围内。王小宁和金勇进从权数控制的角度出发,利用权效应这个系数对几种不同的权数控制方法进行对比研究,同时给出了复杂抽样设计中进行权数调整的控制方案[12]。尽管权数的调整有利于样本单元权数和等于总体规模,保证样本结构和总体结构更加一致,提高了估计精度,但由于调整后的权数差异变大,可能会增加估计量的方差。为了衡量权数带来的影响,本文利用权效应概念来分析相同抽样方法下由权数调整带来的估计量方差的变化。权效应是加权估计量与简单估计方差的比值,它可以反映在相同的抽样方法下由于权数原因对估计方差带来的影响,其计算公式为:
(5)
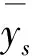
为了使得权数波动在一个可控范围,可使用分位数为5%和95%的权数对整体权数进行截取调整。计算公式如下:
(6)
三、刀切法抽样标准误差计算
对于复杂样本按照理论直接推导出标准误差估计,一则十分困难,二则从节约费用和时间的角度考虑代价也很大。通常采用的替代方法主要有随机组法、平衡半样本方法、刀切法和自助法等。本次老年人调查的抽样设计为四阶段抽样,本身是一个自加权设计,但由于实际调查中遇到诸多情况导致样本单元权重难以按照传统的抽样理论或泰勒展开方法推导出估计量方差的精确或近似计算公式。对于这种复杂样本的估计量的方差估计,通常使用复制样本法来近似估计方差。
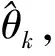
刀切法是由Quenouille等提出的再抽样方法[13-14],其原始动机是降低估计的偏差。刀切法的用法与Bootstrap用法相似,类似于“Leave-one-out”的交叉验证方法。假设x=(x1,x2,…,xn)为观测到的独立同分布的样本数据,n表示总样本量,且该数据服从在空间χ上未知的分布F,即:
xi~F
(7)

定义第i(i=1,2,…,n)个刀切法样本为丢掉第i个样本后的剩余样本,即:
x(i)=(x1,x2,…,xi-1,xi+1,…,xn)
(8)
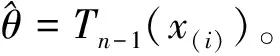
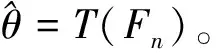
(9)

(10)
这样就得到了基于刀切法的参数θ的标准误差的估计值。胡桂华等人使用分层刀切方差估计来计算抽样方差[15],本文与该文的不同之处在于,一是原文使用了复制权数来剔除第一部样本的一个样本调查小区后,再重新计算剩下的第一部样本调查小区的抽样权数,而式(9)和式(10)通过式(6)进行权数截取后的权数来直接计算参数的估计值,分层信息在权数的调整(式(2)和式(3))中有体现。
四、实证分析
(一)数据来源
对权数的评估需要借助具体的调查数据来进行分析,以老年人调查数据为例进行说明,该调查紧紧围绕老年人生活状况和养老服务需求,重点了解城乡老年人健康、照料护理服务、家庭、经济、社会参与、维权意识与行动、宜居环境以及精神文化生活等方面的状况。调查采取入户访谈和调查问卷收集数据,主要以满足全国代表性需要而抽取样本。调查问卷分为个人问卷和社区问卷,调查对象为居住在中国境内的(不包括台湾省、香港特别行政区和澳门特别行政区)60周岁及以上的中国公民。调查范围为全国各省、自治区、直辖市和新疆生产建设兵团,涉及466个县(区),1 864个乡镇(街道)(每个抽中的县(区)抽4个乡镇(街道)),7 456个村(居)委会(每个抽中的乡镇(街道)抽4个村(居)委会),首次实现覆盖全国范围的调查目标。调查样本规模为22.368万(总抽样比约为1‰)。调查结果数据(2)见http://www.cncaprc.gov.cn/contents/2/177118.html。显示,老年人经济状况得到显著改善,老年医疗卫生工作取得积极进展,老龄产业市场不断升温,老年人社会参与和权益保障工作不断拓展,老年人精神文化生活与时俱进。调查获取的原始数据形式如表2所示。
表 2 列举了部分此次抽样数据,基于地理位置的数据与被访者个人属性的数据可以与第六次全国人口普查的整体数据进行结构对比,结合式(3)进行结构化调整。对权效应的评估选取一个指标,即被访者家庭的平均每月食品支出,是一个连续型变量。对于月均食品支出,可以直接估计其平均值。以全国样本为例,根据式(4)和式(5)得到权数截取前的权效应计算结果为3.87,而根据式(5)和式(6)经过分位数为5%和95%的权数进行截取调整后的权效应变为1.31,有大幅下降并且在可控范围之内。而如果对权数不进行任何调整,仅以设计权数作为最终权数计算的话,权效应为2.86。这也说明权数截取调整使得样本权数变动在一个适当的范围内,比权数截取前也有效地降低了估计量的方差。

表2 老年人调查数据的基本形式
(二)刀切法计算过程
对于目标变量缺失的情况,可以直接删除,也可以采用常用的插补方法进行插补后分析。因本次调查缺失数据较少,所以对缺失数据直接删除。在估计全国老年人月平均食品支出时,利用权数的计算公式如下:
(11)

1.计算每个样本的最终权数。根据被访者的地理属性和个人属性特征,计算其权数值。利用式(1)计算第h个省份的第i个区县第j个街道办事处或乡镇,第k个村(居)委会中抽到的第l个老年人的设计权数Whijkl,即对于相同村(居)委会中老人的权数是相同的。将抽样方案抽样数据和实际得到的样本数据进行比较,利用式(2)进行无回答调整,得到无回答调整后的权数。同时,结合第六次人口普查的年龄、性别数据和样本数据结构特征,结合式(3)计算出各个省的调整系数,利用式(4)得到最终的权数。
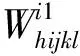
(12)

(13a)
(13b)
其中q=1,2,分别表示权数截取前和截取后的估计。

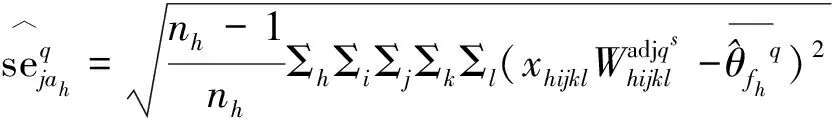
(14a)
(14b)

(三)计算结果分析
结合实际数据,分别利用加权和加权截取后家庭月均食品支出的标准误差进行计算,具体见表3。
从表3可知,全国月均食品支出的加权截取后估计标准误差为2.62,未进行加权截取的标准误差为5.11。各省家庭月均食品支出的加权估计标准误差最大为98.73,经过截取后标准误差变为17.86,各省家庭月均食品支出的估计标准误差加权截取后最大值为北京市的34.88,该省加权的标准误差为33.72;标准误差加权截取后最小值为山东省的5.46,该省加权的标准误差为5.30。综合表3中的数据经过权数截取,可以使得加权后标准误差较大的省份截取后标准误差适当降低,而对于加权误差比较小的省份经过截取后标准误差适当增大,是在可控的范围内,加权截取后的数据从理论上更有说服力,利用了更多的样本信息,也更方便解释。
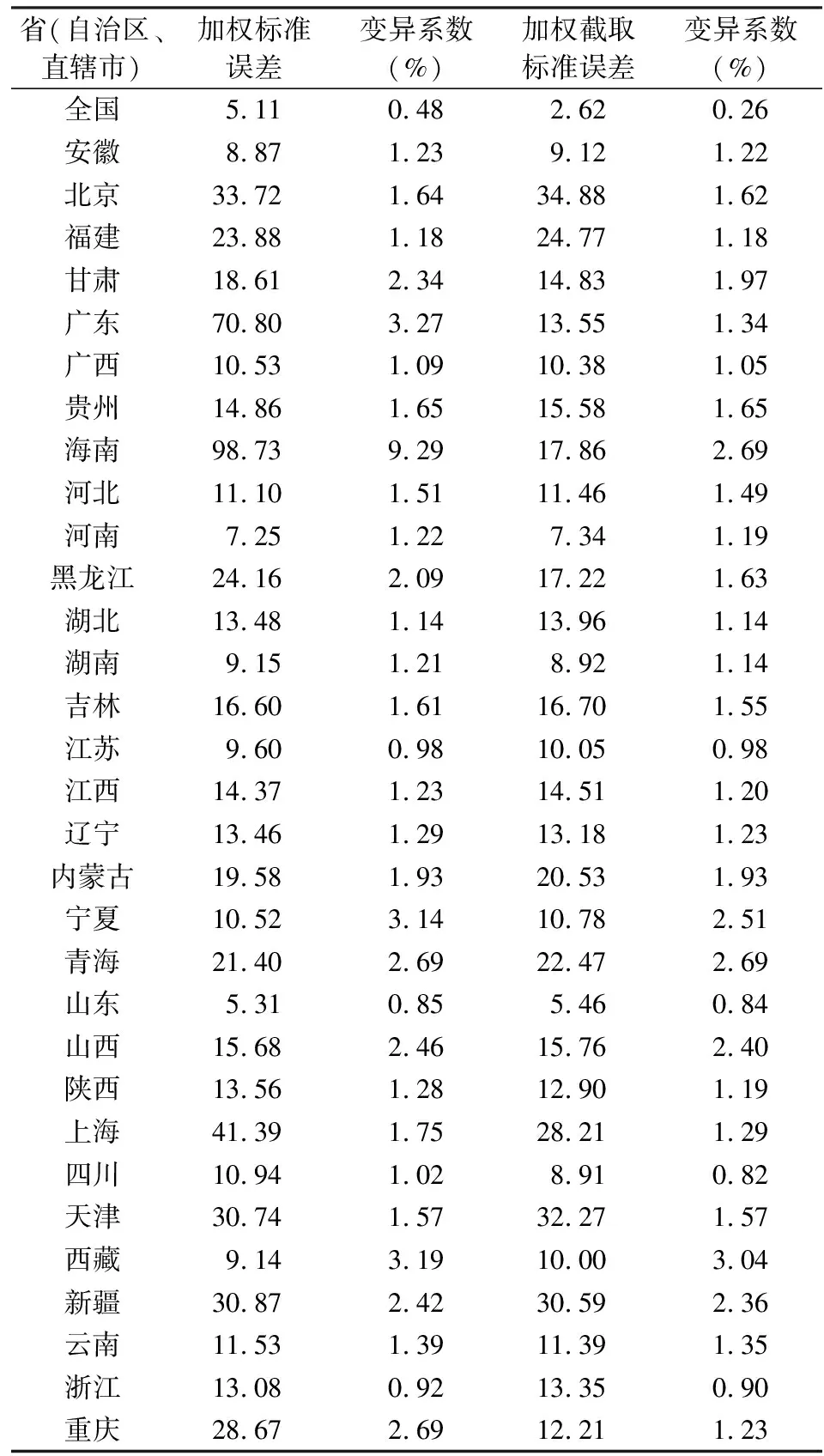
表3 全国和各省加权未截取和截取后家庭
从变异系数(标准误差与平均值的比值,表示数据分布的离散程度)角度来看,全国加权截取后的变异系数为0.26%;从省份上来看,最大值为西藏自治区的3.04%,最小值为四川省的0.82%,但是经过截取后的变异系数降低或保持不变,这也从侧面验证了权数控制的有效性。从以上数据可看出,四川省的月均食品支出相对比较集中,北京市变动比较大,西藏自治区离散程度较高。西藏自治区的变异系数较高,主要是因为该自治区本身的老年人口较少,本次调查的样本量较少,导致估计的相对误差比较大。
五、结论
本文首先探讨了在人口研究中普查数据的应用以及存在的数据质量问题,接着对相关的人口抽样应用问题进行了分析,发现直接利用抽样样本信息来对相关参数进行估计所代表的信息利用不足,进而提出在调查过程中利用权数和权数控制以解决这一问题。针对抽样中的权数问题,从权数的计算、权数的无回答和结构调整、权数的控制以及基于权数计算的变量的标准误差出发,结合老年人调查数据进行了详细的分析和说明,同时强调了权数在抽样调查中的重要性。权数虽在一定程度上增大了参数估计的标准误差,但是从代表整体信息的角度上来看,比单纯地利用样本信息进行估计更具有代表性。为了让权数更有效地代表样本,避免因权数过大或过小对估计的标准误差造成大的影响,本文分别在实际数据中利用原始加权数据和加权截取(控制)数据进行了分析,结果显示在参数估计的过程中,对权数进行一定的控制能适当降低估计的标准误差,同时能降低估计变量的变异系数,在一定程度上能有效地提升分析的质量和增加调查信息的认可度。

