一种基于WLS的电网分层状态估计方法研究

（上海恒合电力工程有限公司，上海 200000）

1 引言

电力系统遥信遥测可能存在不良数据。例如，某一个节点有3条支路，流向该节点的电流实际值为i1、i2、i3，测量值为，根据基尔霍夫电流定律，有i1+i2+i3=0；但是由于测量存在误差，一般--≠0。这样的测量数据不能直接用于计算，必须要经过适当的处理。这个处理的过程就称为状态估计。

电力系统状态估计即在测量误差时，运用实时量测系统的冗余度提高测量精度，排除随机干项导致的数据错误，最终通过数学计算估计出系统的运行状态，得到可靠的并且为数最少的系统状态变量值。

2 电网分层网络状态估计思想

如图1所示，是一段配电网的简单模型。

图1 小型配电网模型

对这个电网的模型进行网络拓扑可以得到：

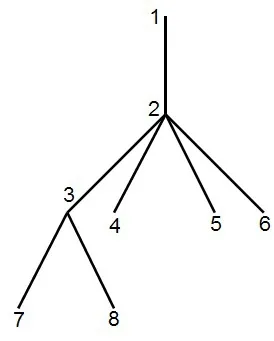
图2 配电网拓扑结构

由于配电网呈辐射形、树枝状，单源而且没有回路。考虑到电网的分层，可以采用从叶子节点一层一层地往根节点推进的方式进行状态估计。如图2所示，共有8个节点，每个节点都有测量仪器的测量数据。以各节点注入的有功功率为例，在不考虑损耗的情况下，各点的有功功率应该满足：

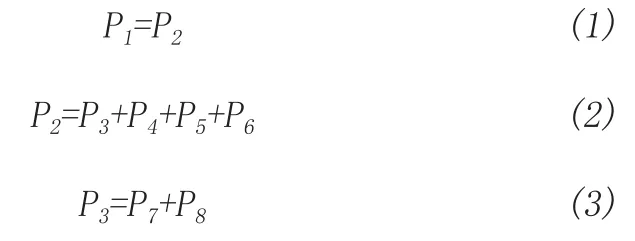
但是测量得到往的数据往往不能满足这样的条件。本文采用的方法是从网络拓扑图的最底层开始，逐层向上使用加权最小二乘法进行优化求解，并将得到的新数据作为往上一层进行加权最小二乘法求解时的伪量测量。由于伪量测量是经过一次初次处理的数据，权重不再是该点量测数据的原来的权重，故应该对这个权重进行修正。

3 节点权重的修正

3．1 二层二叉树节点权重修正

考虑一棵简单的二层二叉树，它有3个节点：父亲节点Z以及2个儿子节点X、Y。3个节点的关系方程为z=x+y。设3个点的量测平均值分别为x0、y0、z0，量测方差分别为D(x0)、D(y0)、D(z0)。通过加权最小二乘法对3点进行优化，即求x、y、z使得下式最小：

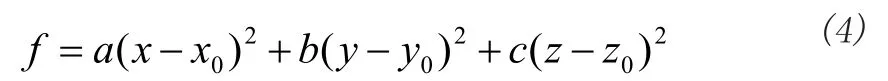
其中a、b、c分别为X、Y、Z 3点的权重，可用测量值的方差的倒数作为该点的权重的初始值。由于a、b、c 三者皆为正实数，因此式（4）可以化为：

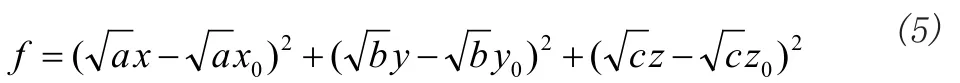
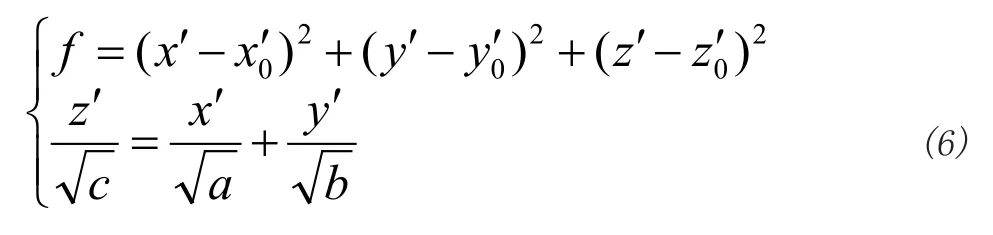
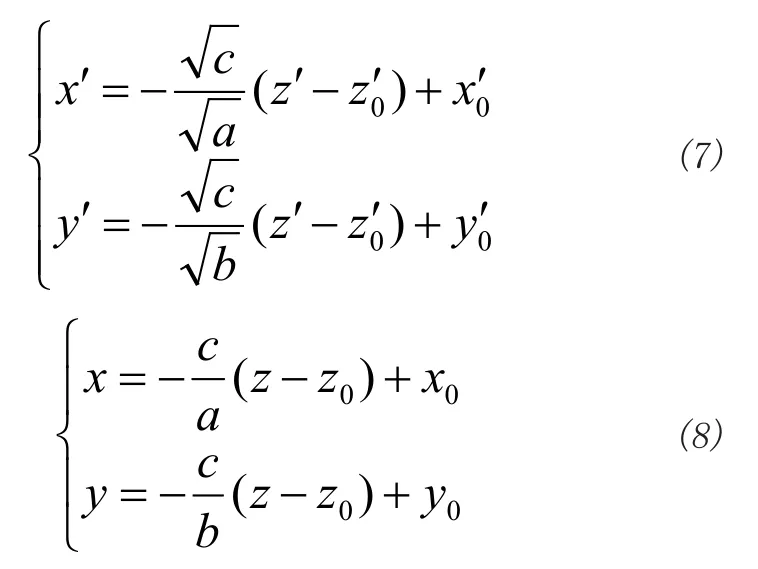
将式（8）带入关系方程z=x+y，可得：

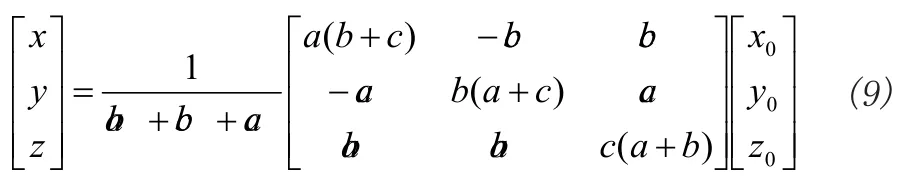
式（9）即为3个节点估计值的表达式。根据上面对权值的定义，已知x0、y0、z0的方差分别为又已知方差的性质：若X与Y相互独立，则有：

因此可得：

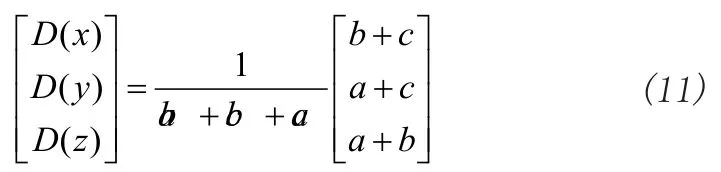
3．2 二层多叉树节点权重修正

设某二层多叉树有1个根节点和n个叶子节点。根节点为Y，初始权重为a0；n 个叶子节点依次为Xi（i=1,2,…,n），对应的初始权重依次为ai(i=1,2,…,n）。利用二层二叉树的权重修正方法可得：

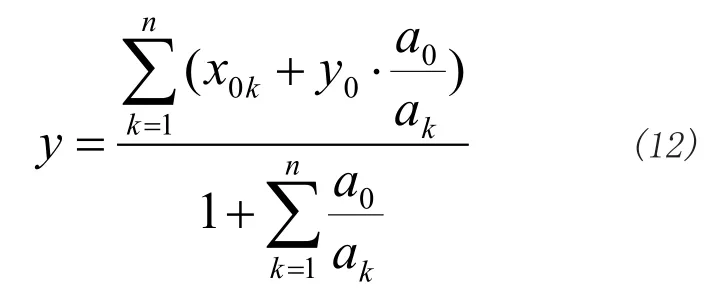
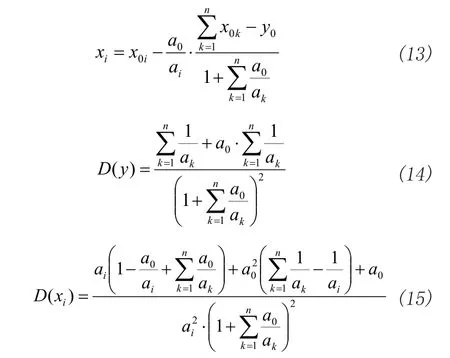
4 算例分析

以图2的拓扑结构及式（1）～（3）的约束关系为例，给定各点的真实值，并在真实值上添加信噪比为40dB的高斯白噪声，每个点选取10个测量数据，将其平均值作为量测值，方差作为量测方差。重复采用式（12）～（15）进行最小二乘状态估计，可以得到表1。

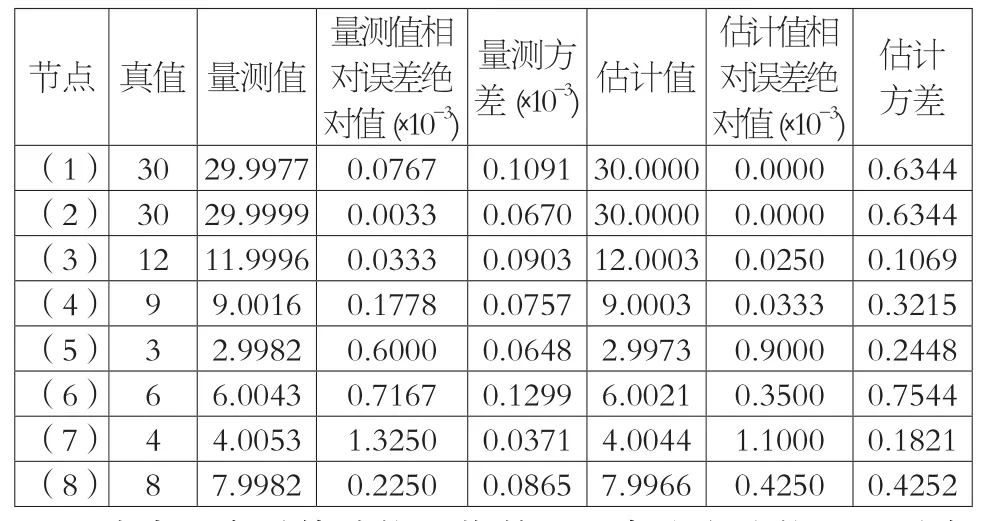
表1 模拟网络状态估计计算结果

迭代3次后估计值可收敛到1个稳定的值，可见有权重修正的状态估计的有着较快的收敛速度。从表1中数据可知，量测数据在状态估计后精度有明显的提高，但某些节点的估计值可能会有更大的偏差。

5 结语

电力系统状态估计是电力系统分析的重要根据。在过去几十年里，状态估计取得了很大的发展，也提出了很多有待解决的问题。本文提出了一种配电网的状态估计时权重值的修正算法，该算法原理同样适用在其他网络中，根据网络的拓扑结构可以得到不同的约束关系方程，进一步可以推导出估计值和修正后的权重的表达式。