一族新的微分方程的守恒律和Darboux变换

何国亮， 郑真真

(郑州轻工业大学 数学与信息科学学院 河南 郑州 450002)

0 引言

在理论物理和数学物理中，用带谱参数λ的Lax对去发现新的可积系统是一个有意义的研究领域.可积系统的另一个关键特征是它们具有无穷多守恒律[1-2].具有Lax表示的可积系统可以用反散射变换方法[3-4]、代数几何方法[5-7]、Darboux 方法[8-9]及其他方法[10-13]求解，尤其是起源于1882年Darboux对Sturm-Liouville方程进行研究时所提出的Darboux变换方法，它是一种获得演化方程精确解[14-16]的非常有效的方法.

文中我们给出了一个与3×3矩阵谱问题相关的新的非线性演化方程族，并且通过考虑两个相关的线性谱问题，得到了这个方程族中前两个非线性演化方程的无穷多守恒律

(1)

(2)

最后，通过引入3×3矩阵谱问题的规范变换，得到了方程(1)的Darboux变换，并由此给出一些精确解.

1 非线性演化方程族和无穷多守恒律

本节，我们首先引入一个以u，v为位势,λ为常谱参数的3×3矩阵谱问题

(3)

然后借助于零曲率方程得到与之相联系的非线性演化方程族.为了推导相对应的非线性演化方程，我们定义两组Lenard递推方程

(4)

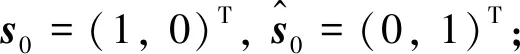
(5)

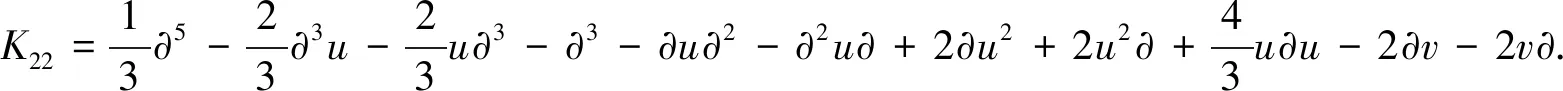
(6)

接下来，我们考虑静态零曲率方程

(7)

它等价于

(8)

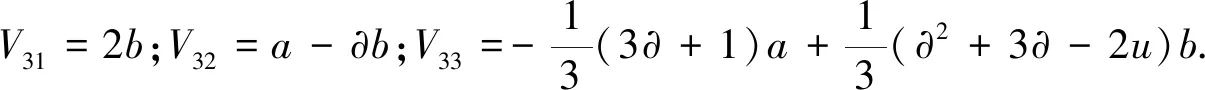
(9)

把式(9)代入式(8)，可以得到

KSj=JSj+1，j≥0；JS0=0.

(10)

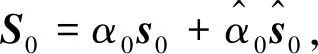
令ψ满足谱问题(3)和辅谱问题

(11)

(utn，vtn)T=KSn=JSn+1，n≥0.

(12)

该方程族的前两个方程为

(13)

225uxuxx+180u2ux+72uux+4ux+9vxxx+135vvx+54uxv+54uvx+3vx)；

36uuxxx-72uxuxx+36vvx+96u2ux+8uux).

(14)

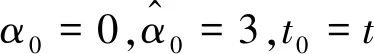
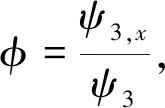
φxx+3φφx-φx+φ3-φ2-2uφ=ux+v+λ.

(15)

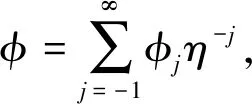
(16)

另外，由辅谱问题可以得到

(17)

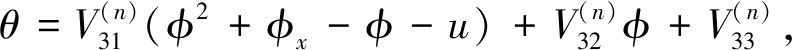
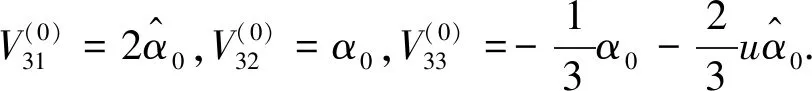
把φ的展开式和上式代入到式(17)中，可得

(18)

我们把φ和θ的展开式中的系数φj和θj叫作守恒密度及连带流.方程(13)的第一个守恒律为

(19)

对于方程(14)，当n=1时，

(20)

此时

(21)

方程(14)的第一个守恒律为

(22)

2 方程(1)的Darboux变换和精确解

本节，我们将通过Darboux变换给出方程(1)的精确解.该方程所满足的Lax方程为矩阵谱问题(3)和如下辅谱问题

(23)

从图6可以看出，试验数据与数值模拟数据在各测点的压力值基本上是一致的，经计算风门全开时炉排表面的横向配风不均匀系数ηQ试验数据为51%，数值模拟数据为57%，该数值模拟方法有一定的准确性，可以选用该数值模型进行数值模拟研究。

其中：

(24)

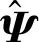
(25)

(26)

(27)

其中：

(28)

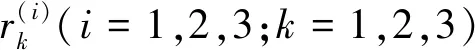
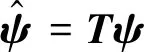
(29)

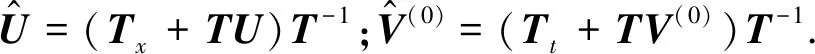
(30)

新旧位势之间的变换公式为

(31)

下面通过变换式(31)，我们构造方程(1)的精确解.易见方程(27)可以改写为

(32)

b=Δ1/Δ；c=Δ2/Δ；d=Δ3/Δ，

(33)

其中：

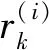
(34)

1) 取u=0，v=-λ时，式(3)和式(23)有基解矩阵

(35)

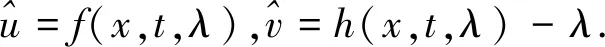
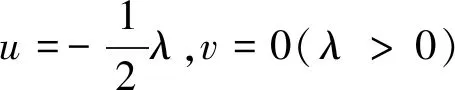
(36)

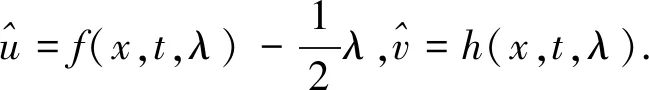
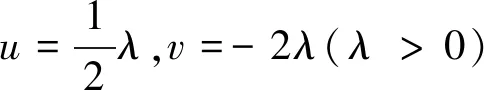
(37)

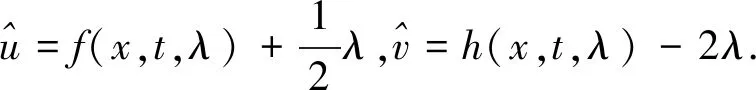
4) 取u=0，v=0时，式(3)和式(23)有基解矩阵

(38)

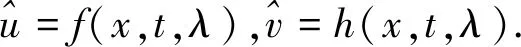
3 结论

本文我们引入了一个具有两个位势的3×3矩阵谱问题，通过该问题及其辅助谱问题得到了一个新的微分方程族. 基于特征函数的Riccati方程，我们推导出该方程族前两个方程的无穷多守恒律，并借助于Darboux变换得到了第一个非平凡方程的一些显式解. 关于这个非线性演化方程族的孤子解、Bäcklund变换、代数几何解和其他的一些性质，我们将在以后的文章中进行讨论.