基于SPEA-Ⅱ算法的SDN多控制器优化部署机制

郭梦娜， 王兴伟， 张闯闯， 黄 敏

(1. 东北大学 软件学院 辽宁 沈阳 110169； 2. 东北大学 计算机科学与工程学院 辽宁 沈阳 110169； 3. 东北大学 信息科学与工程学院 辽宁 沈阳 110819)

0 引言

广泛使用的移动设备、蓬勃发展的大数据、云计算及虚拟化技术激发了对网络容量和扩展性的新要求，同时这又导致了现有的网络设备安装、配置复杂度的飞快上升.面对这些问题，SDN可以发挥其优势[1].SDN解耦网络的控制平面与数据平面，将“智能”集中在控制平面，控制平面中的控制器通过可编程接口集中控制交换机，交换机仅按照控制器的“指示”处理数据包.SDN控制器及其合理部署可以提高网络资源利用率、简化网络的管理以及减少操作开销，并且可以极大提高网络的性能.早期的SDN架构中控制平面通常只有一个控制器，Floodlight[2]、Maestro[3]等都是典型的单控制器.然而单控制器无法应对网络中流量过大的情况，而且单控制器明显会成为网络的瓶颈，一旦发生单点故障，网络将会整体瘫痪.为了解决单控制器的上述问题，HyperFlow[4]、FlowVisor[5]等多控制器案例相继被提出，但这些多控制器大都存在弱一致性问题，而且维持控制器的一致性会消耗大量时间，导致系统的性能下降.

目前国内外已有不少学者致力于多控制器部署方面的研究，也取得了很多优秀的研究成果.文献[6]提出了一个容量控制器布局的数学模型，其优化目标是最小化交换机与控制器之间的最坏情况时延.文献[7]提出了一种混合整数线性程序的控制器布局策略，其优化目标包括交换机到距离其最近控制器以及最近控制器到第二近控制器的时延.文献[8]提出了LiDy+算法，将交换机到控制器时延及网络流量的动态性考虑在内，解决了控制器动态部署的问题.文献[9]提出了双向匹配策略及相应的控制器部署方案，考虑的目标包括时延及控制器负载.文献[10]基于NSGA-Ⅱ 算法，考虑了交换机到控制器的时延、控制器之间的时延以及节点和链路故障.文献[11]提出了一种基于密度的控制器放置方法，利用基于密度的交换机聚类算法将网络分成几个子网络，并在每个子网络中部署一个控制器，考虑了控制器与交换机之间的时延、控制器数量与交换机失效情况.文献[12]提出了一种快速有效的进化算法来解决大规模多目标控制器放置问题，考虑的目标包括交换机到控制器的时延、控制器之间的时延及网元故障.以上研究关注交换机到控制器的时延、控制器之间的时延等因素，解决了多控制部署问题.然而，同时考虑时延、交换机拥有从控制器数量及控制路径故障率的研究还较少.因此，本文提出一种基于SPEA-Ⅱ 算法的SDN多控制器优化部署机制，在给定控制域的情况下，建立了多控制器优化部署数学模型；综合考虑交换机到控制器的时延、控制器之间的时延、控制路径故障率和平均交换机拥有从控制器数量4个优化目标，提出了基于SPEA-Ⅱ 算法的多控制器优化部署机制.仿真结果表明，相较于基准算法，该机制可以在一定程度上提高网络的可靠性.

1 多控制器优化部署数学模型

将网络建模为无向带权图G(V,E)，其中V与E分别表示交换机集合和链路集合.n和m分别表示交换机数目和链路数目，边权重eij表示网络时延.将网络划分为多个控制域，用1,2,…,k表示，第i个控制域中交换机节点的编号用i1,i2,…，iq表示，q为节点总数.

假定每个控制域中只有一个控制器，称为此控制域内交换机的主控制器，主控制器位于该控制域内的某一个交换机节点处.除主控制器以外，交换机还会被分配给位于其他控制域中的控制器，称为此交换机的从控制器.只有当主控制器失效后，从控制器才会接管此交换机.部署方案的解为CP=[c1,c2,…,ck]，ci为控制域i中控制器所处节点的编号，C={c1,c2,…，ck}为控制器集合.X=[xij]n×k代表交换机到其主控制器的分配矩阵，若交换机i的主控制器是控制域j中的控制器cj，则xij=1，否则xij=0.Y=[yij]n×k代表交换机到其从控制器的分配矩阵，若交换机i的从控制器是控制域j中的控制器cj，则yij=1，否则yij=0.本文中控制路径是指交换机与主控制器之间和任意两个控制器之间最短路径的集合，用path={path1,path2,…,paths}表示，其中s可以表示为

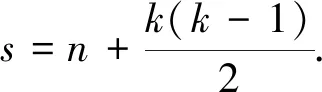
(1)

网元(包括交换机和链路)集合用L=V∪E={l1,l2,…，lw}表示，其中w=m+n.ei表示网元li所处控制路径的数量，交换机到控制器的最大时延为Dmax，节点i和j之间的传播时延为d(i,j).

为了加快算法收敛，基于最小化交换机到主控制器的时延进行控制器的初步部署.将初步部署问题简化为：遍历控制域内所有交换机的位置，计算此控制域中所有交换机到此位置的平均时延ls，使得ls最小的位置即为主控制器初步部署的位置.ls可以表示为

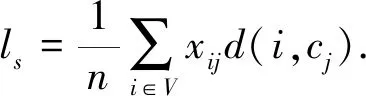
(2)

接下来加入了其他3个优化目标，对控制器的部署方案进行优化.本文的优化目标可以表示为

minF(CP)=[f1(CP),f2(CP),f3(CP), -f4(CP)],

(3)

式中：CP表示控制器的部署方案；f1(CP)、f2(CP)、f3(CP)、f4(CP)分别表示最小化交换机到控制器的时延、最小化控制器之间的时延、最小化控制路径故障率、最大化平均交换机拥有从控制器数量这4个优化目标，具体可以表示为

(4)

控制路径故障率是指平均每个网元故障所造成的故障控制路径数量占总控制路径数量的比例.约束条件为：

1)xijd(i,cj)≤Dmax，即交换机到其主控制器的时延不可超过最大时延；

2)yijd(i,cj)≤Dmax，即交换机到其从控制器的时延不可超过最大时延；

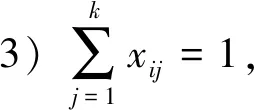
4)xijyij=0，即交换机的主、从控制器不能相同；

5)i1≤ci≤ip，即控制域i中的控制器只能位于此控制域中的节点上；

6)ci≠cj，即任意两个控制器不可处于相同节点上.

2 算法设计

2.1 基于SPEA-Ⅱ算法的多控制器优化部署机制

SPEA-Ⅱ[13]算法为SPEA的改进算法，在适应度计算和环境选择等方面均有改进，而且在求解高维度优化问题上，此算法的解集分布更加均匀.SPEA-Ⅱ算法的基本步骤如下.

Step 1： 初始化.对控制器初步部署中得到的初始解进行交叉或变异，获得由N个解构成的初始种群.初始化Dmax，由初始种群和Dmax得到分配矩阵X和Y、控制路径集合path以及每个网元li所处控制路径的数量ei.计算出每个个体的4个目标函数值，创建空的归档集集合，并将迭代次数t置为0.

Step 2： 适应值计算.计算此次迭代中归档集集合和种群集合中个体的适应值.

Step 3： 环境选择.拷贝归档集集合和种群集合中非支配个体进入下一代归档集集合，并对下一代归档集集合的大小进行控制.

Step 4： 终止.如果迭代次数达到预先设定的最大值T或满足停止条件则算法停止，将下一代归档集中的非支配个体拷贝到集合A中，即为结果集合，否则进入Step 5.

Step 5： 配对池选择.使用二进制锦标赛算法选择归档集中的个体放入配对池中.

Step 6： 交叉和变异.将配对池中的个体取出，经交叉和变异生成子代，并保存到下一代种群中.迭代次数加1，转到Step 2.

设M和N分别为优化目标函数的数量和种群大小，初始化阶段的时间复杂度为O(N)，适应值计算阶段的时间复杂度为O(MN2)，环境选择阶段的时间复杂度为O(MN3)，终止阶段的时间复杂度为O(1)，配对池选择阶段的时间复杂度为O(N)，交叉和变异阶段的时间复杂度为O(N2).因此，此算法的时间复杂度应为O(MN3).

2.2 基于熵权多目标决策法的唯一解选择机制

2.2.1熵权 假定评估问题有a个待评项目和b个评价指标，建立多对象关于多指标的非模糊评价矩阵R=(rij)a×b，rij表示评价指标j下项目i的评价值.评价指标j的熵权值为

(5)

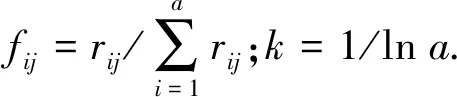
2.2.2算法流程 基于熵权多目标决策法的唯一解选择机制的基本思想为：使用熵权多目标决策法，从多个非支配近似最优解中选择出一个最优解，作为最终的控制器部署方案.算法具体流程如下.

1) 形成分析评价表.Pareto解集中第1层的n个解作为n个方案，4个优化目标作为4个因素，方案分析评价表如表1所示，其中bij是相应方案j中优化目标i的目标函数值.

表1 方案分析评价表Tab.1 Plan analysis evaluation table

2) 标准化分析评价表.按照式(6)所示的损失性指标的标准化公式标准化表1中的值.

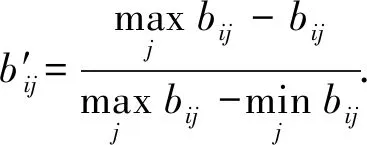
(6)

3) 计算熵权值.根据式(5)计算各因素的熵权值Hi.H1、H2、H3、H4分别表示平均交换机到主控制器时延的熵权值、最大控制器之间时延的熵权值、平均控制路径故障率的熵权值、平均交换机拥有从控制器数量的相反数的熵权值.借助各因素的熵权值，得到如式(7)所示的Hi规格化属性矩阵.

(7)

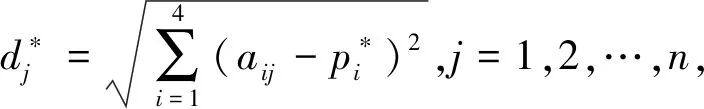
(8)

(9)

式中：Oj=(a1j,a2j,a3j,a4j)T；Tj∈[0,1].

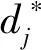
控制器部署方案的伪代码如算法1所示.

算法1基于熵权多目标决策法的唯一解选择机制.

输入：方案分析评价矩阵analysis4*N；输出：控制器放置方案CP.

BEGIN

1. 计算所有方案在4个指标上的最大值max和最小值min；

2. FORi←1 TO 4 DO

3. FORj←1 TONDO

4. 根据max，min以及式(6)标准化analysis矩阵得到analysis′；

5. END FOR

6. END FOR

7.kk←1/logn；

8. 根据式(5)和kk计算熵H；

9.analysis′←analysis′*H；

10. 根据式(8)计算被评对象到理想点P*的距离；

11. 根据式(9)计算被评对象与理想点的贴近度；

12. 根据距离和贴近度对方案进行排序；

13. 选出最优控制器放置方案CP；

END

3 仿真实验与性能评价

3.1 仿真实验

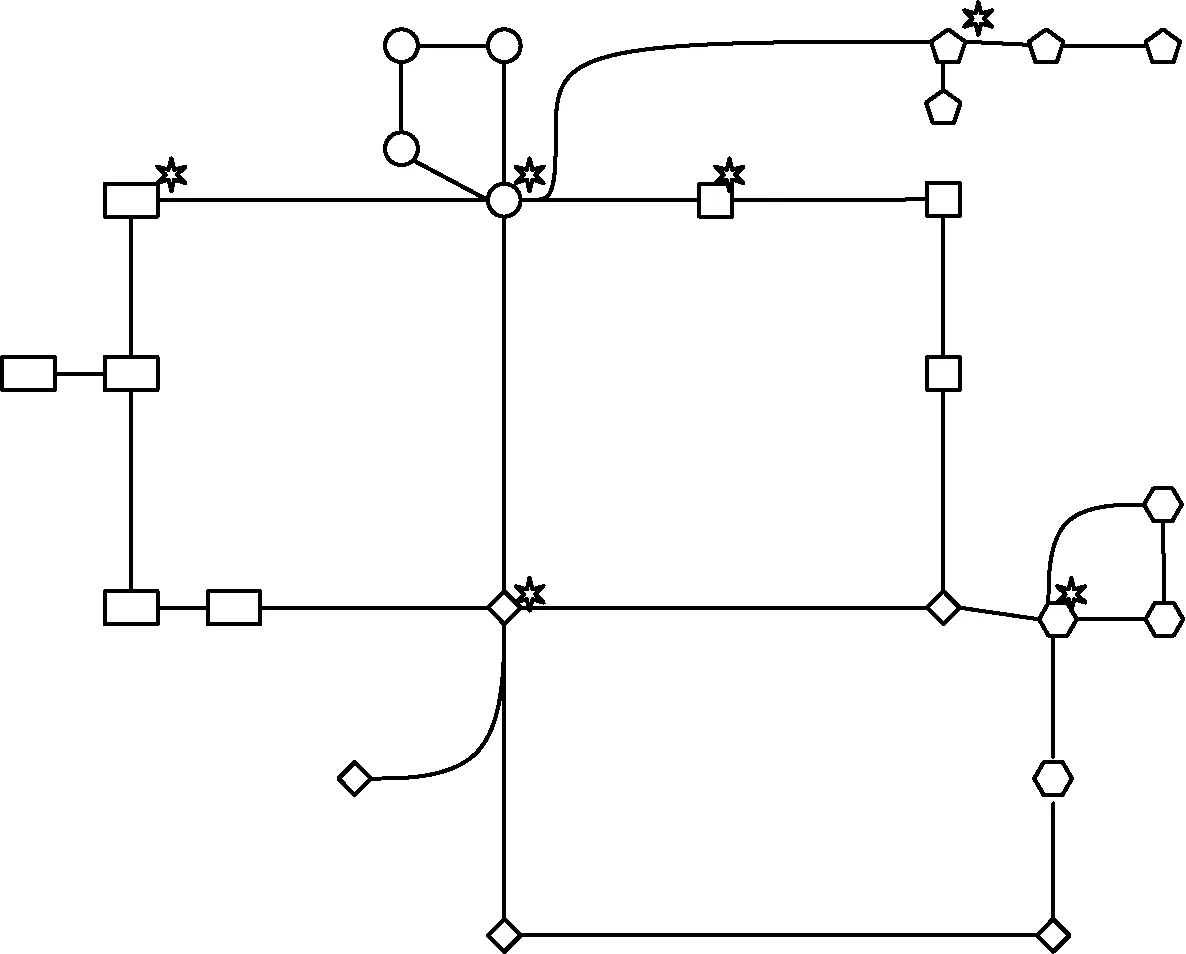
图1 控制器部署方案Fig.1 Controller deployment scheme

采用第2代中国教育科研计算机网CERNET2[14]作为测试拓扑，该拓扑节点数量和边数量分别为25和29，选用的开发工具为Matlab，开发环境为Windows 7.实验参数设置为：种群大小为200，最大迭代次数为30，交叉率与变异率分别为0.8和0.1，得到的控制器部署方案如图1所示.相同形状代表同一个控制域，右上角标有六角星图案的图形代表控制器所在的位置.

3.2 性能评价

为了对本文提出的SDN多控制器优化部署机制(简称S机制)进行评价，选择了文献[15]中的机制(简称M机制)与文献[10]中的多目标优化机制(简称MN机制)作为对比算法.其中M机制中控制器的部署考虑的是最小化交换机到控制器的时延.本文选择交换机到控制器时延、控制器之间时延、控制路径故障率、交换机拥有从控制器数量作为4个评价指标.图2显示了不同控制器数量下交换机到控制器时延的变化曲线.可以看出，交换机到控制器时延随控制器数量的增加而减小，这是因为控制器数量越多，网络中控制域数量就越多，平均每个交换机到其所属主控制器的时延就会越小.在不同控制器数量下S机制的时延要比M机制增加8%～38%，这是因为M机制仅仅考虑了最小化交换机到控制器的时延.S机制的交换机到控制器时延要略大于MN机制.图3显示了不同控制器数量下控制器之间时延的变化曲线.可以看出，控制器数量增多之后，控制器之间时延也随之增加了，这是因为整个网络被划分成更多的控制域，导致控制器的部署范围更广阔，从而使得控制器之间时延增大.S机制控制器之间时延要比M机制减少5%～20%，主要是因为M机制在放置控制器的时候没有考虑最小化控制器之间的最大时延.S机制与MN机制在控制器之间时延上基本持平.

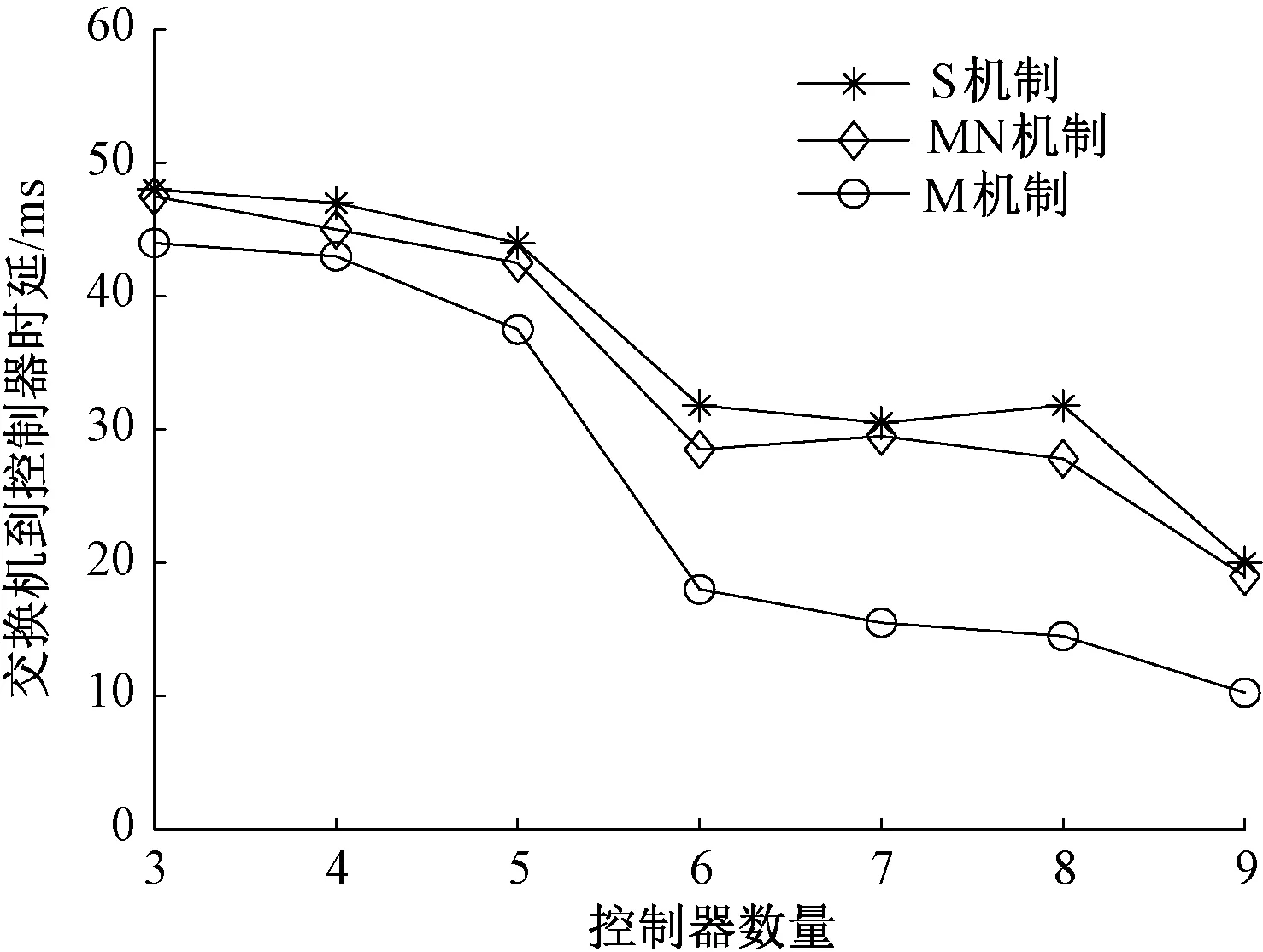
图2 交换机到控制器时延的变化曲线Fig.2 Variation curve of delay between switch and controller

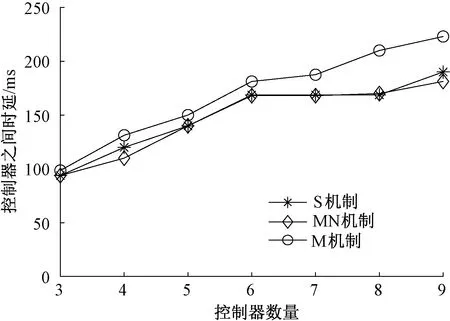
图3 控制器之间时延的变化曲线Fig.3 Variation curve of delay between controllers

图4显示了不同控制器数量下控制路径故障率的变化曲线.可以看出，控制路径故障率随控制器数量的增多而逐渐减小，这是因为当控制器数量增多时，交换机到其主控制器的最短路径数量不变，与此同时，控制器之间的控制路径数量增多，此时总控制路径数量的增幅大于平均每个网元故障所造成的故障控制路径数量的增幅.由于M机制在部署控制器的时候，优化目标并没有考虑控制路径故障率，所以S机制的控制路径故障率比M机制减少23%～46%.S机制在控制路径故障率上与MN机制基本持平.图5显示了不同控制器数量下平均交换机拥有从控制器数量的变化曲线.可以看出，平均交换机拥有从控制器数量随控制器数量的增多而增加.控制器数量增多，意味着每个交换机满足时延约束的控制器的数量也会增加，可能成为交换机从控制器的控制器数目就会增加.同样是因为M机制没有对该指标进行优化，S机制平均交换机拥有从控制器数量比M机制要增加20%～32%.与MN机制相比，S机制平均交换机拥有从控制器数量要略多一点，这主要也是由于MN机制没有考虑这一优化目标.

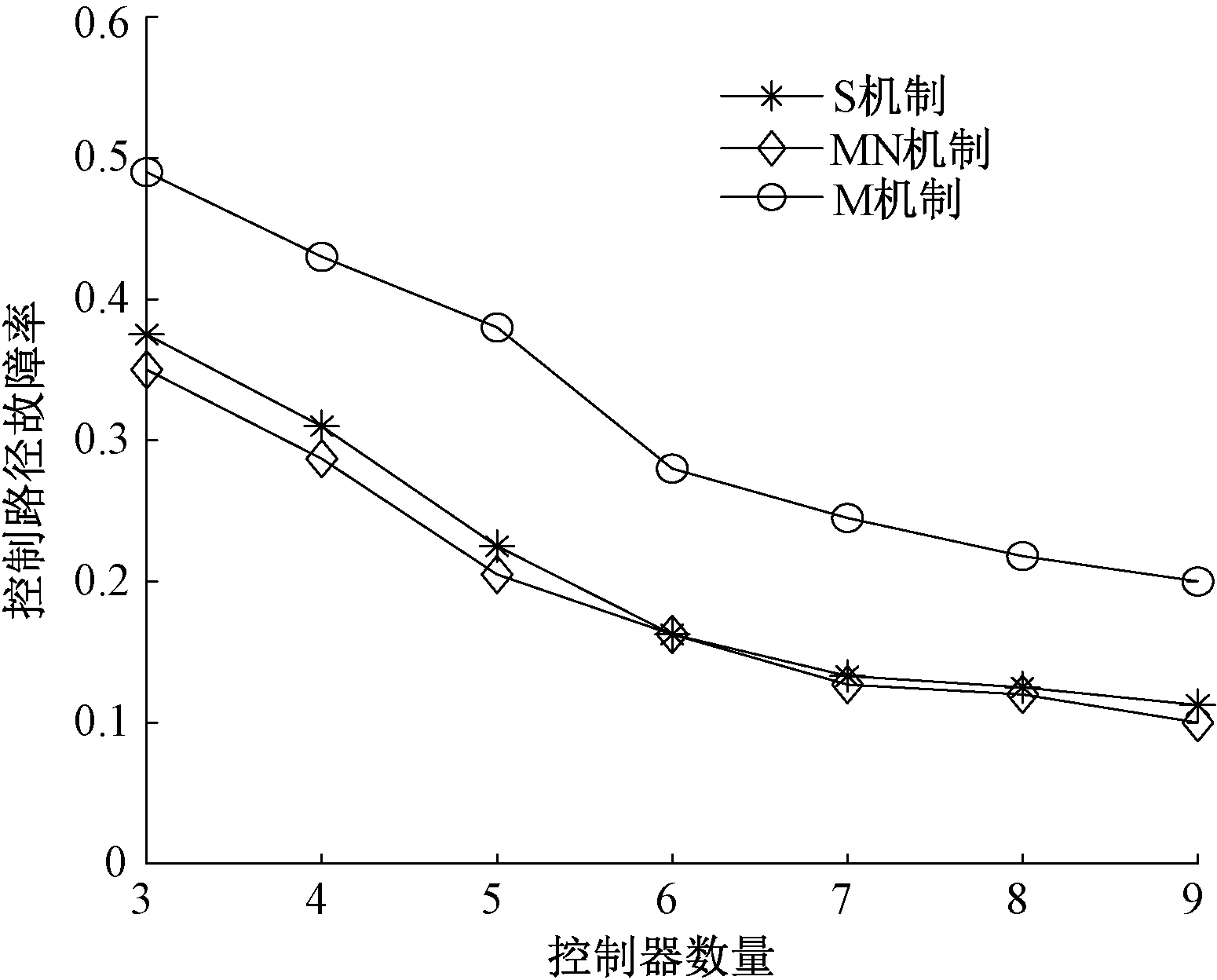
图4 控制路径故障率的变化曲线Fig.4 Variation curve of control path failure ratio

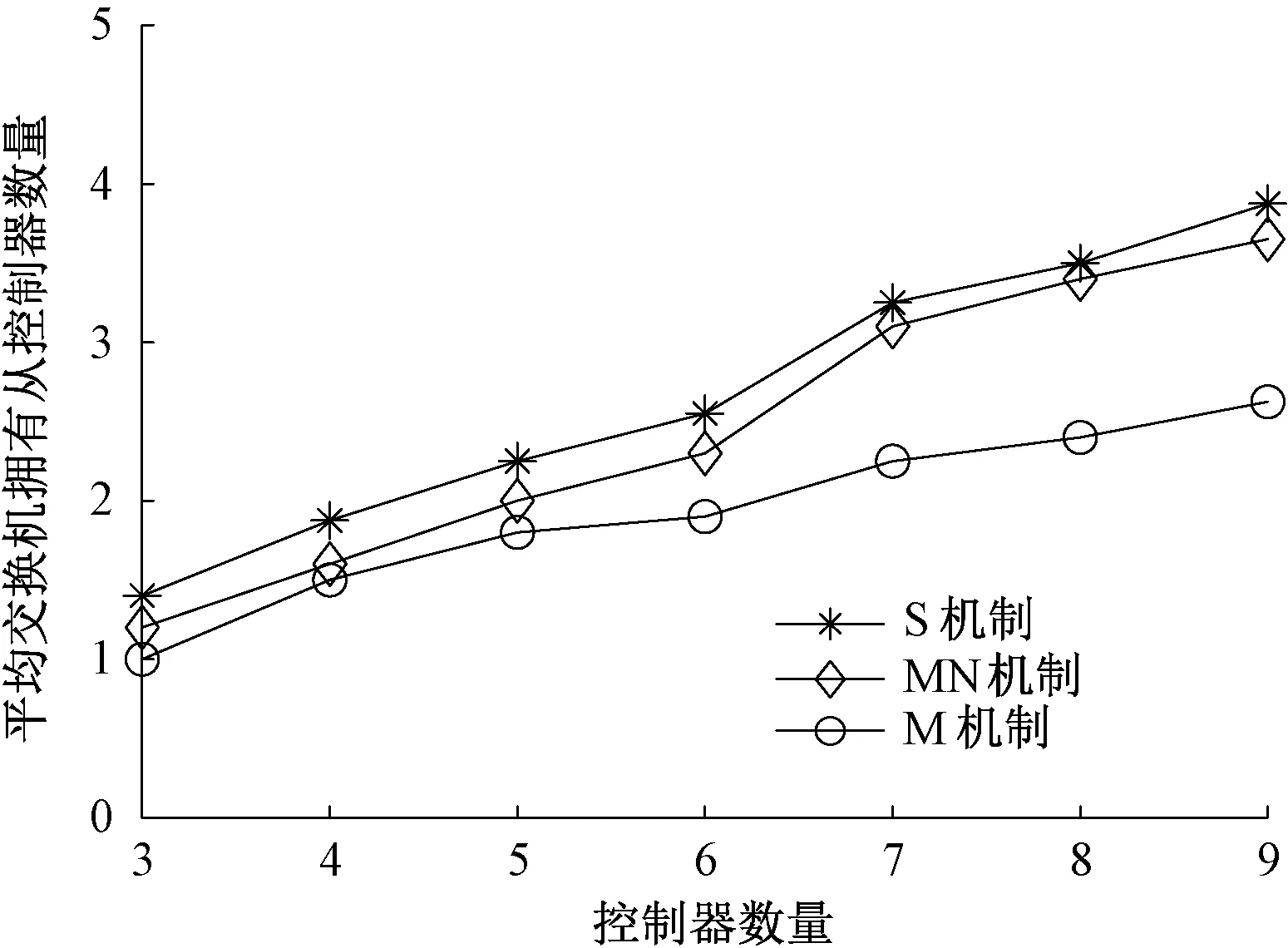
图5 平均交换机拥有从控制器数量的变化曲线Fig.5 Variation curve of average number of slave controllers belonging to switches

与M机制相比，本文提出的S机制的交换机到控制器时延略高，然而在控制器之间时延、控制路径故障率、平均交换机拥有从控制器数量方面优势明显.与MN机制相比，本文提出的S机制的交换机到控制器时延略高，然而其能有效提高平均交换机拥有从控制器数量.

4 小结

本文首先对多控制器部署及其优化问题进行了数学描述，对控制器进行了初步部署.通过分析控制器部署问题建立了包含4个优化目标在内的数学模型，并利用SPEA-Ⅱ算法针对这4个目标函数提出了控制器部署的优化机制.同时，提出了基于熵权多目标决策法的唯一解选择机制.仿真结果表明，本文提出的多控制器优化部署机制可以在一定程度上最小化时延，提高网络的可靠性.本文仅考虑了网络静态的情况，而实际网络中的流量是动态变化的；此外，本文假定每个控制域中仅放置一个控制器，而实际网络中，特别是大规模网络中，一个控制器往往是难以满足网络需求的.因此，今后的工作重点将集中在扩大网络规模和考虑网络流量的动态性.