电子交易中保护消费者隐私相关性分析

陈文倩， 赵 岚,2， 张亦茹

(1. 湖北工业大学 计算机学院 湖北 武汉 430068； 2. 湖北工业大学 工业大数据协同创新中心 湖北 武汉 430068； 3. 广州中学 广东 广州 510000)

0 引言

电子交易被越来越多的消费者接受并广泛使用[1]，文献[2]揭示若消费者数据没有得到妥善处置，攻击者可对消费者状态及行为进行分析、预测，从而造成严重影响[3].如何保护数据隐私和防止敏感信息泄露成为当前面临的重大挑战[4]. 因此交易平台的信息安全管理问题已成为关注热点.西密歇根大学发表的一份报告表明，顾客只会访问有积极印象的网站，因此分析顾客信息来提高服务是很有必要的[5].目前统计相关分析中的相关系数可用于交易中的推荐系统，我们将针对消费者信息的相关性分析进行隐私保护研究.

针对统计分析过程中暴露消费者隐私等安全问题，现有方案主要集中在保护系统免受外部攻击和进行简单数据分析[6].文献[7]用分布式方法计算相关性但效率较低，文献[8]在效率上有所提高，但是不能有效地防止内部攻击.类似还有以公钥为基础的解决方案[9-13]，通常比对称加密的方案效率低，且这类方案中的数据处理只能给出简单统计处理.

针对电子交易数据分析过程中保护消费者隐私问题，本文提出了有效解决方案：对大量消费者数据分块，通过安全信道传输给多服务器储存，只要其中一个服务器没被攻破，则该系统是安全的；采用Paillier同态加密数据并控制访问权限，仅授权分析者能访问数据并实现数据分析；实现密文下的相关性分析处理方法，运用相关性分析实现多属性间相关性分析，并保护消费者个人隐私信息.

1 Paillier 公钥密码算法

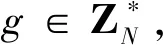
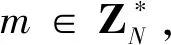
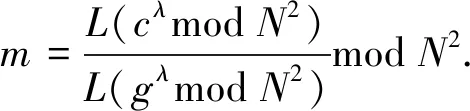
4) 加法同态性质. 给定两个明文m1和m2，则有E(m1+m2)=E(m1)×E(m2).

2 消费者隐私的数据相关性分析方案

2.1 系统角色与模型

图1表示所提出的系统模型的结构，包括3个实体.

消费者C：消费者在购物过程中产生电子交易信息(身份、购买商品、浏览记录等)，这些信息被分离成多块分别发送给对应服务器.

数据服务器S：每个数据服务器对收到的数据加密并存储.接受到分析者的查询请求，服务器间配合完成密文上的安全计算，对于不同合法请求给予不同密文.

分析者V：可能是行为分析者、研究者等需要相关性分析结果的人员.仅完成身份注册的分析者才能在查询时获得符合自己权限的密文，对密文解密和整理，得到最终需要的统计相关分析值.

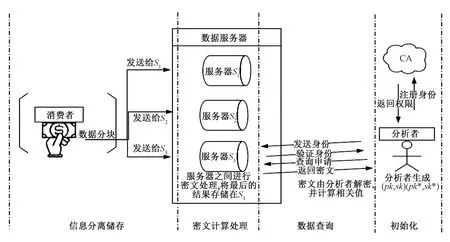
图1 系统模型图Fig.1 System model

本模型考虑两种攻击模式：外部攻击者和内部攻击者.外部攻击指模型之外的攻击者在不知道私钥下，从系统中了解消费者信息.内部攻击是指系统参与者，如服务器或分析者试图从方案中学习并还原敏感信息等恶意行为.假设数据服务器和分析者都是半诚实的，即准确执行协议但会试图挖掘隐私.为便于描述，图1中服务器数量为3，但方案适用于更多情况.模型中涉及3部分的通信：消费者与服务器之间、服务器之间、分析者与服务器之间.

2.2 具体方案

假设系统中存在公共密钥基础设施(public key infrastructure, PKI)，其中存在证书颁发机构(certificate authority,CA).分析者根据Paillier加密算法生成两对公私钥对(pk,sk)和(pk*,sk*).分析者在服务器上完成注册,CA将包含(pk,pk*)的数字证书发送给分析者.出于安全原因，Paillier算法中N应不低于1 024 bt.

2.2.1信息分离储存 若将消费者信息发送给同一个服务器，服务器尝试分析消费者数据则会暴露其隐私，为有效防止内部攻击，我们设立了多数据服务器.运用文献[14]的方法，将单个隐私信息ηi随机分为3个整数(根据数据服务器数量分配)，ηi=λi+μi+νi，i=1,2,…，n，n表示消费者个数.消费者Ui将λi发送给S1，将μi发送给S2，将νi发送给S3.

2.2.2密文计算处理 假设有n个消费者，每个消费者有3个属性X、Y、A，X=(x1,x2,…,xn),Y=(y1,y2,…,yn),A=(a1,a2,…,an)，(xi,yi,ai)为同一消费者Ui的信息.xi=λi+μi+νi，yi=λ′i+μ′i+ν′i，ai=λ″i+μ″i+ν″i，i=1,2,…,n.安全计算需要3个算法：算法1用来在密文域中进行处理，使解密之后得到属性的平均值；算法2解密后可得到同一属性存储在各服务器的分块信息乘方和；算法3解密之后可得到两个属性存储在各服务器的分块信息的乘积和.具体过程如下.

算法1平均分析算法.

输入：X=(x1,x2,…,xn)，xi=λi+μi+νi，i=1,2,…,n；

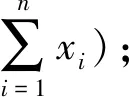
1. 令Cx=1；

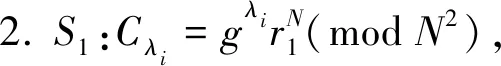
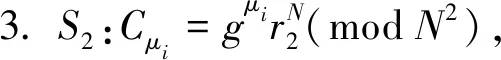
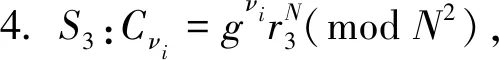
5.i从1～n按上述步骤循环，当i=n时结束；

6.S3存储最后得到的Cx值.

算法2乘方循环算法.

输入：X=(x1,x2,…,xn)，xi=λi+μi+νi，i=1,2,…,n；

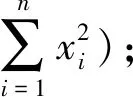
1. 令Cx2=1；

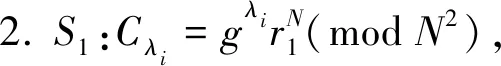
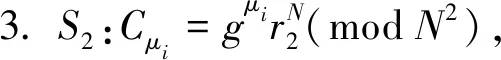
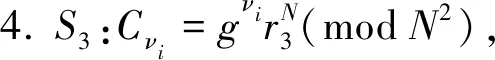
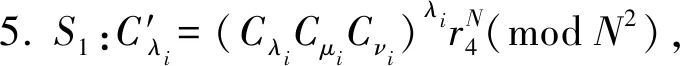
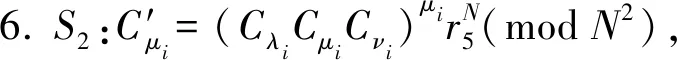
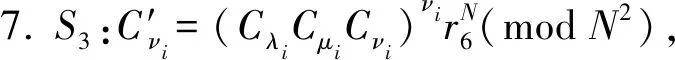
8.i从1到n按上述步骤循环，S3存储Cx2值.

算法3相关循环算法.

输入：X=(x1,x2,…,xn)，Y=(y1,y2,…,yn)，xi=λi+μi+νi，yi=λ′i+μ′i+ν′i，i=1,2,…,n；

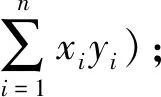
1. 令Cxy=1；

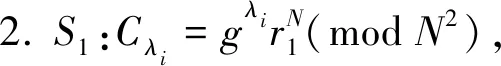
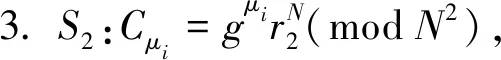
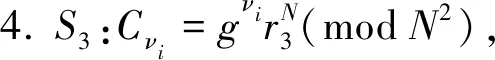
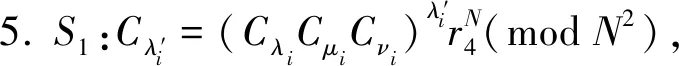
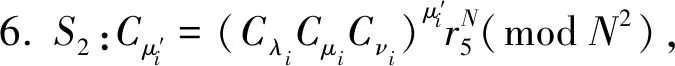
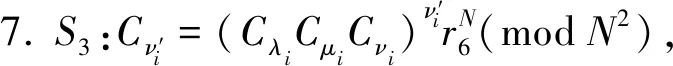
8. 将i从1到n按上述步骤循环，S3存储Cxy值.

2.2.3数据查询 本文设计控制访问权限，分析者查询结果前需发送查询请求，包含查询消息、对查询消息的签名、数字证书、时间戳等.服务器检查时间戳与当前时间吻合，再验证签名，若签名正确，则服务器相信查询请求由授权分析者提供.根据不同请求，服务器返回相关的密文.由分析者解密并整理计算.

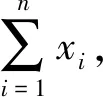
(1)

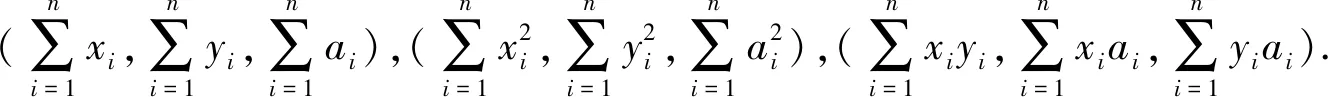
(2)

其中X与Y的相关性为

(3)

同理可得到X与A的相关性rXA，Y与A的相关性rYA，从而计算出半偏相关系数.

3) 若查询的是消费者的属性X与Y都除去属性A的影响后的偏相关系数.分析者得到的密文同上，解密后整理计算偏相关系数为

(4)

4) 若分析者查询属性Y与X、A的复相关系数.分析者得到的密文同上，解密之后整理计算，

(5)

3 正确性与安全性分析

3.1 正确性分析

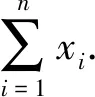
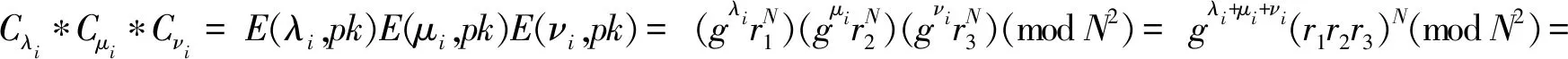
定理5数据查询过程中分析者查询的是相关系数，则得到的密文是Cx,Cy,Ca,Cx2,Cy2,Ca2,Cxy,Cxa,Cya；解密得到

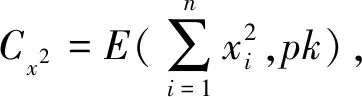
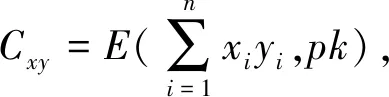
3.2 安全性分析

本方案设计3个安全目标，具体如下.

1) 数据存储安全， 密钥存储安全，信息存储安全，密文存储安全.

证明方案初始阶段，公私钥和签名验证钥通过安全信道来进行传输的.信道的秘钥可通过Diffie-Hellman密钥交换协议[15]或者RSA等公钥密码系统建立.通过安全信道可以实现数据的保密性、真实性和完整性，因此密钥的存储是安全的.在消费者和服务器间的通信中，消费者数据分离基于SHA-3生成，任何外部攻击和内部攻击，即服务器被攻陷或服务器之间勾结，在没有密钥的情况下都不能猜出分块整数，数据分块目的是防止服务器分析数据进行内部攻击,方案假设至少有一个服务器不被攻破，存放在服务器内的数据是安全的.同时使用Paillier加密算法对数据加密，在密文域上完成安全计算且将值存储在服务器S3中.Paillier的困难问题没有解决，则加密过程是安全的，外部攻击者无法得到存储的数据，密文的存储是安全的.因此本文提出的方案达到数据存储安全.

2) 数据分析安全. 即使破解了任一服务器或多服务器合谋也不会泄露消隐私信息.

证明数据分析过程是在3个服务器交互中且在密文域上完成的.加密系统是完善的，分析过程中任何一个交互过程，外部攻击者没有私钥下都无法获取消费者的隐私数据.另外，可在3个数据服务器之间使用公钥系统再建立一个安全信道以增加方案的安全系数.服务器都是半信任模型，且分析过程中没有解密步骤，即使出现内部攻击即多个服务器合谋，甚至拿到了存储在S3的最关键的密文，也无法分析得到完整的原始隐私数据和相关统计分析值.因此本文提出的方案实现了数据分析安全.

3) 数据查询安全. 仅合法命令才能获得计算结果.

证明查询阶段，服务器验证分析者的签名和时效性，仅将符合权限的查询结果以密文的形式返回给授权分析者，因此避免了恶意外部攻击.坏的情况是分析者得到结果前，足够强大的外部攻击者拦截下密文并解密，但这样获得的是还未整理的值，若不知整理计算过程，信息与随机数无法区分，因此保证了数据的隐私性.更坏的情况是授权分析者与服务器勾结能在此过程中获得数据，但由于至少一个服务器不被攻破，攻击者只能得到部分统计数据且不涉及原始隐私信息，甚至S3也参与勾结，在系统的最后也不会提供任何原始个人隐私信息的查询.因此方案实现了数据查询安全.

4 性能分析

本文采用Paillier同态加密算法解决密文下相关性计算问题，基本运算是模指数运算，加密或者解密一次需要进行两次模指数运算.信息分离存储过程中使用文献[14]中基于SHA-3随机数生成方案.方案中3个算法和总相关性分析及与文献[7]和[8]算法复杂性比较如表1所示.

表1 复杂性分析Tab.1 Complexity analysis

5 结论

本文对电子交易中消费者数据的储存和统计计算方面的安全隐私问题进行了探讨，并提出了一种高效的解决方案，设计了安全计算方法，使得各服务器协作在密文上完成统计分析，保证了消费者隐私.通过访问控制确保仅授权分析者能获取相关性分析值.最后进行了正确性、安全性和技术性能分析.