磁声发射励磁器的仿真分析

沈功田1，闻庆松，沈永娜1，李志农

(1.中国特种设备检测研究院，北京 100029；2.南昌航空大学 无损检测技术教育部重点实验室，南昌 330063)

许多学者研究发现，MAE与材料所受到的应力状态和微观组织有着明显的依赖关系，因此可将MAE技术应用于铁磁性金属材料残余应力[2]、塑性变形[3]、热处理状态[4]、疲劳[5]和蠕变[6]的评估中。

对MAE进行检测时，励磁器起着至关重要的作用，其主要由U型磁轭和线圈组成。磁轭本身不产生磁场，只是起着磁力线的传输作用。使用过程中在线圈两端施加交变的电压信号，然后通过线圈将变化的电压信号转化为交变磁场，通过磁轭和被测的铁磁性试件组成磁回路，从而达到磁化材料的目的。图1为进行MAE研究时常采用的检测系统框图。

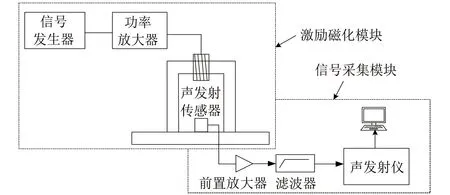
图1 MAE检测系统整体框图

根据MAE的产生机制[7]，在试样被充分磁化至饱和的情况下，其产生的MAE信号效果最好，包含的信息最为丰富。但在采用电压驱动线圈产生交变磁场时，由于功率放大器最大的输出电压有限，且最大的放大倍数为一定值，U型磁轭的励磁能力受到限制，而不同的磁感应强度会影响到MAE信号的产生效果，进而直接影响到检测结果。所以，提高现有MAE检测装置的励磁能力尤为重要。

U型磁轭在与试样接触时，会存在着一定的空气间隙，如图2所示。根据安培环路定理，闭合路径上试样的磁场强度(H3)，线圈的匝数(N)和流入线圈的电流(I)的关系如式(1)所示。

NI=∑(H1l1+H2l2+H3l3)

(1)

式中:H1为磁轭l1段的磁场强度;H2为空气l2段的磁场强度;H3为试样l3段的磁场强度。

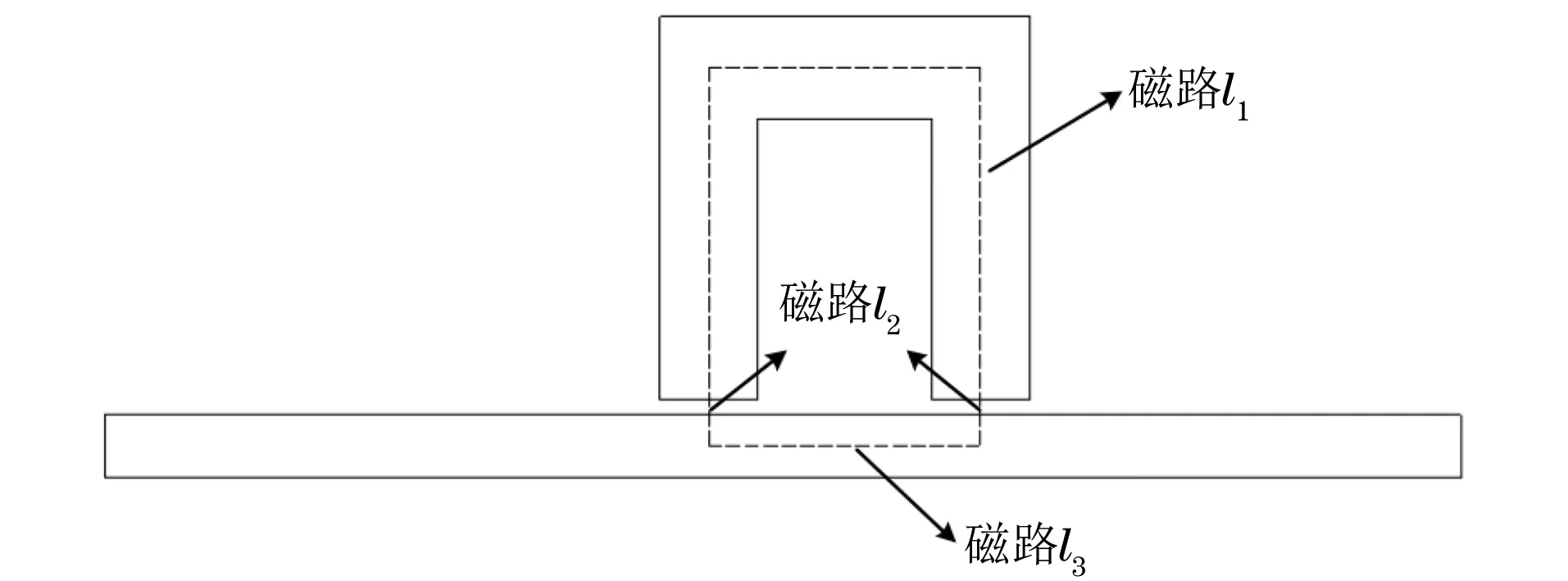
图2 导磁回路的磁路示意

由式(1)可知，试样产生的磁场大小主要取决于整个导磁回路安匝数和磁路长度，但当磁轭的线圈匝数、功率放大器的输出电压和磁路一定时，磁轭两磁极之间的间距、磁极的厚度和线圈的缠绕方式也会对试样的磁化效果产生影响。

假定波浪载荷引起砂质海床孔隙水的渗流满足达西定律，渗透系数为常数，海床为各向同性介质。基于比奥动力固结方程，海床的控制方程为：

因此，利用ANSYS Maxwell电磁场有限元仿真软件对不同尺寸的磁轭和线圈缠绕方式进行仿真，以此来验证上述因素的变化对试样磁化效果的影响，从而找出磁化效果最优的励磁尺寸。

1 有限元仿真模型的建立

磁场有限元模型的建立以Maxwell方程组为出发点，式(2)～(6)是Maxwell方程的数学微分表达式，式(6)为电通密度D与电场强度E的关系。对MAE励磁器进行仿真优化分析时，主要用到式(2)和式(3)。

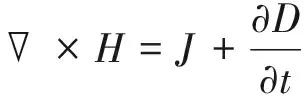
(2)

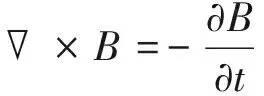
(3)

(4)

(5)

D=εE

(6)

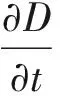
根据MAE检测系统中的励磁装置，建立如图3所示的三维有限元模型，模型主要由U型磁轭、励磁线圈和Q235钢试样组成。为了更接近于真实的检测环境，材料属性的定义要与实际材料的一致或者相近。模型的各部分材料设置如下：U型磁轭采用具有高磁导率、低矫顽力、低损耗的DW310_35型硅钢片；励磁线圈采用的是线径为0.5 mm的铜线，绕制过程中保持绕行方向一致，绕制匝数为864匝，施加的激励电压大小为40×sin(2×π×10×t) V；试样选取尺寸(长×宽×高)为220 mm×40 mm×8 mm 的Q235钢；求解边界为真空。有限元仿真需要设置这4种材料的磁性参数，但这些参数在实际情况下会随励磁频率的不同在一定范围内变化，因此根据仿真条件的实际需求，设定了如表1所示的材料参数。试验过程中，为了避免线圈与磁轭直接接触而造成短路，在磁轭与线圈之间填充了绝缘胶布，因此仿真时在线圈与磁轭之间设置间隙为0.1 mm厚度的空气层。

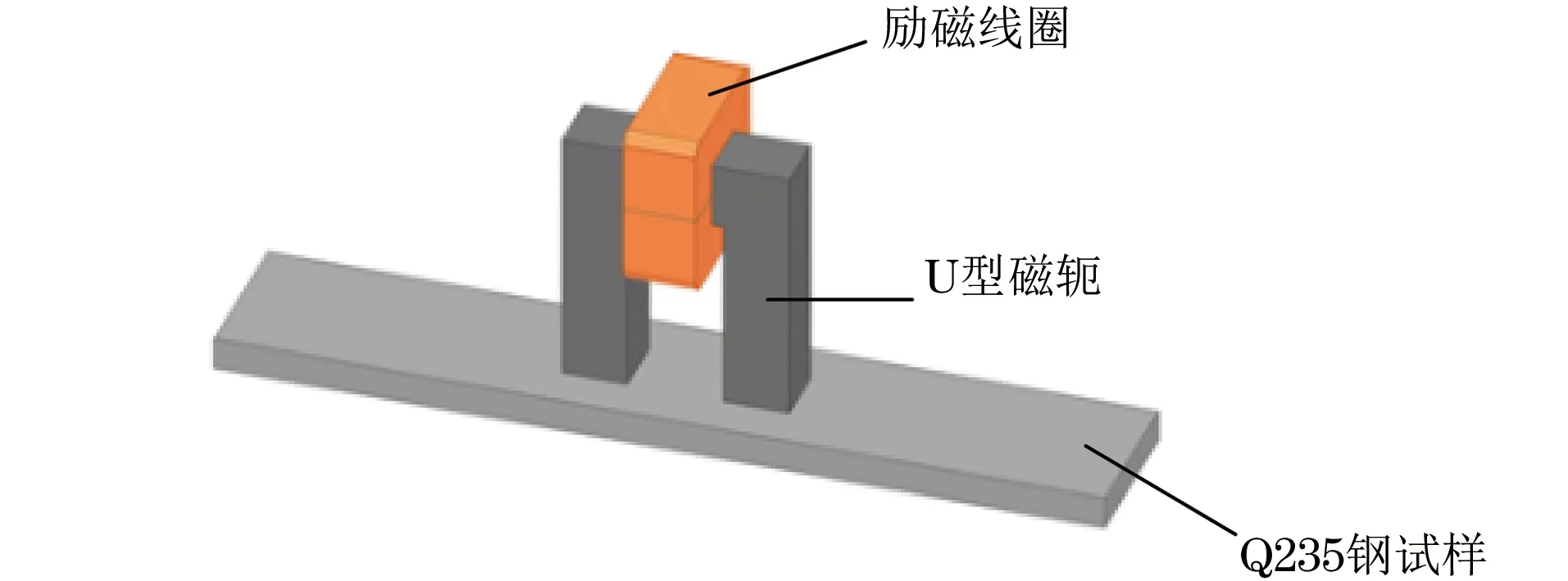
图3 励磁器模型结构示意

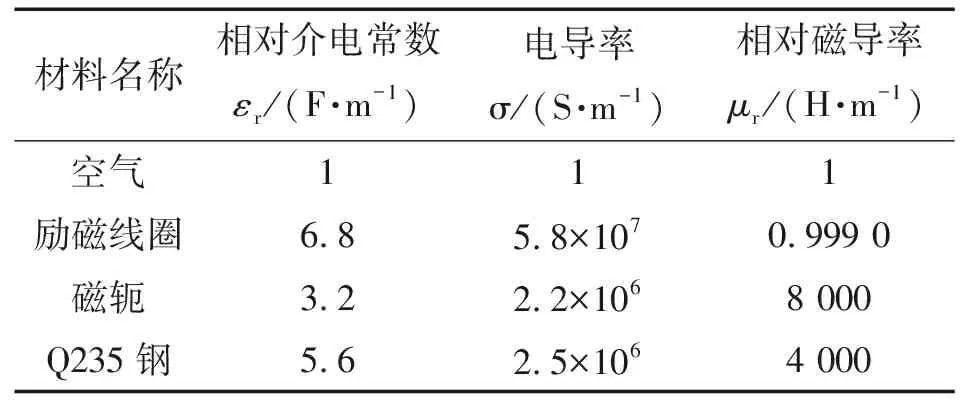
表1 材料参数

2 仿真结果及其分析

2.1 不同磁极间距的仿真结果分析

磁轭磁极间距的不同，会影响整个导磁回路的磁阻抗。为了探究磁极间距的变化对试样磁化效果的影响，根据安培环路定理，在保持总磁路不变的情况下，设计了6组磁极间距不同的磁轭，磁轭尺寸示意如图4所示(图中L为磁极间距，a为磁极宽度,b为磁极厚度，H为磁轭高度)，6组U型磁轭的尺寸参数见表2。6组磁轭的磁路长度均为192 mm。

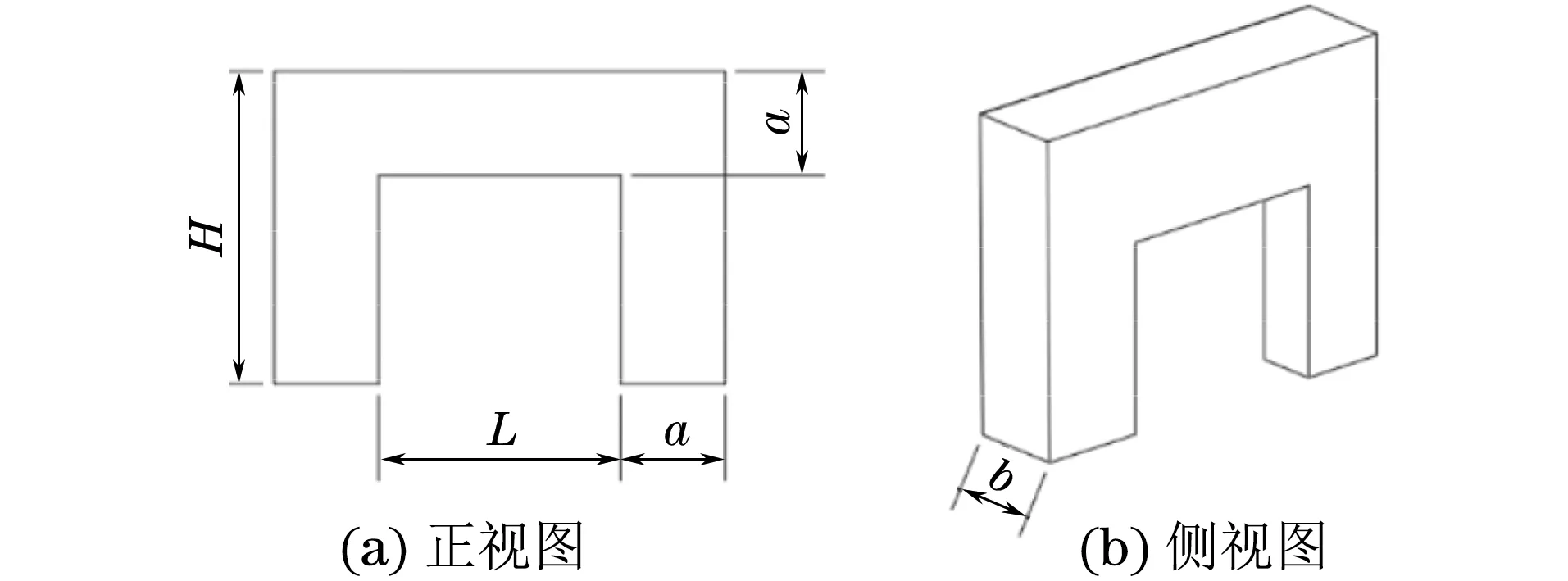
图4 磁轭尺寸示意

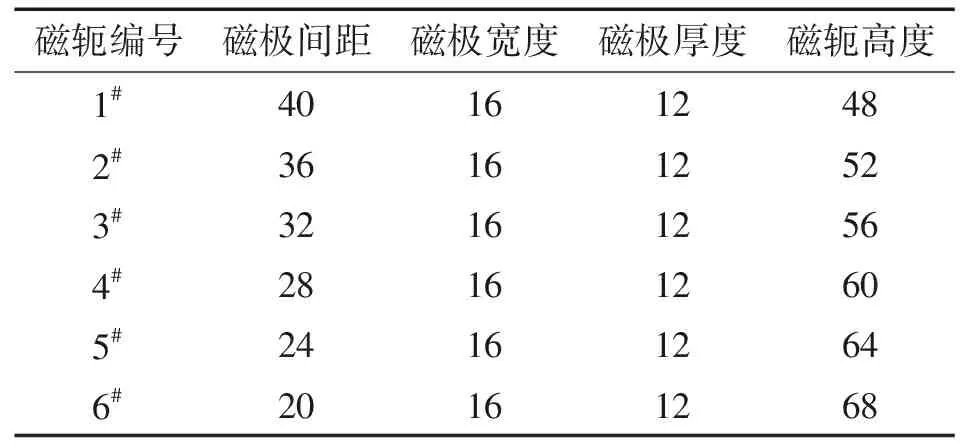
表2 各磁轭的尺寸参数 mm

1#磁轭励磁时线圈的输入电压和电流的大小示意如图5所示。从图5中可以看出，由于线圈通入电流后存在自感电动势，电流明显滞后于电压，而后整个瞬态场在0.2 s之后趋于稳定。

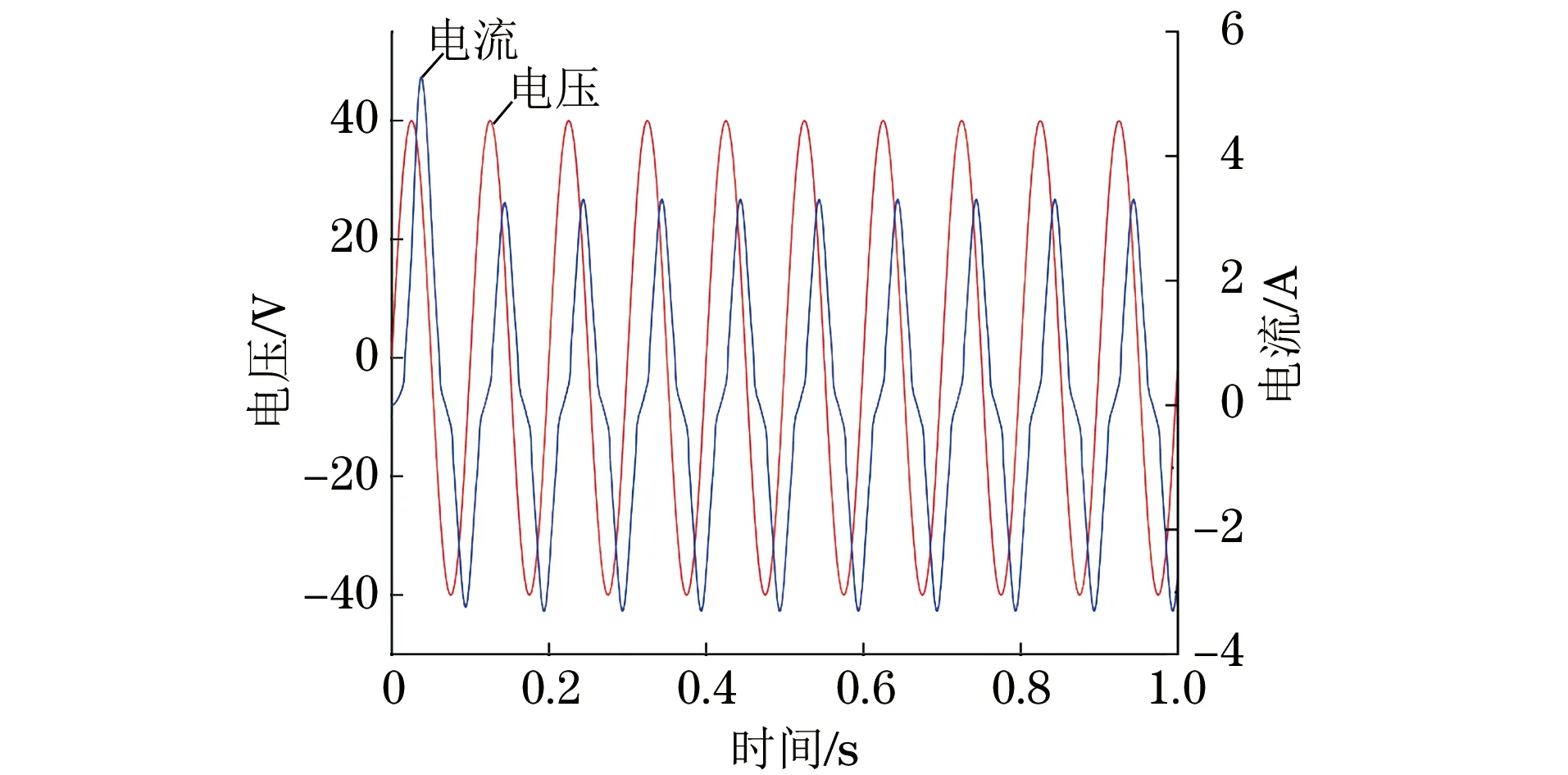
图5 励磁线圈的电压和电流示意

在磁化电流最大值对应的瞬态时刻观察导磁回路的磁感应强度分布，磁化效果如图6所示。可以看出:磁轭与试样材料组成了导磁回路，试样表层部分达到了被磁化的效果。整个磁化区域集中在磁轭两极附近：其中磁轭两极之间的Q235钢表面的磁化效果最好，远离磁轭两极部分的磁化效果较差。

图6 导磁回路的磁感应强度分布云图

为了更加直观形象地观察到Q235钢试样内部的磁场变化情况，选取试样中心位置的3个分析点(分别位于表面0 mm,近表面0.5 mm和中心深度4 mm 处)来观察这3点的磁感应强度变化情况，从而观察Q235钢试样内部的磁化效果。图7为1#磁轭中深度为0.5 mm的分析点在整个瞬态电磁场稳定后，随时间变化的趋势，从图中可以看出，该点的磁感应强度随着电流的改变呈周期性变化，其最大值时刻与线圈励磁电流的最大值和最小值对应的时刻相一致。

图7 1#磁轭的磁感应强度随时间的变化趋势

用同样的方法查看其余5组磁轭磁感应强度的变化情况，然后提取出每组磁轭的最大磁感应强度。不同深度下磁感应强度的变化示意如图8所示。

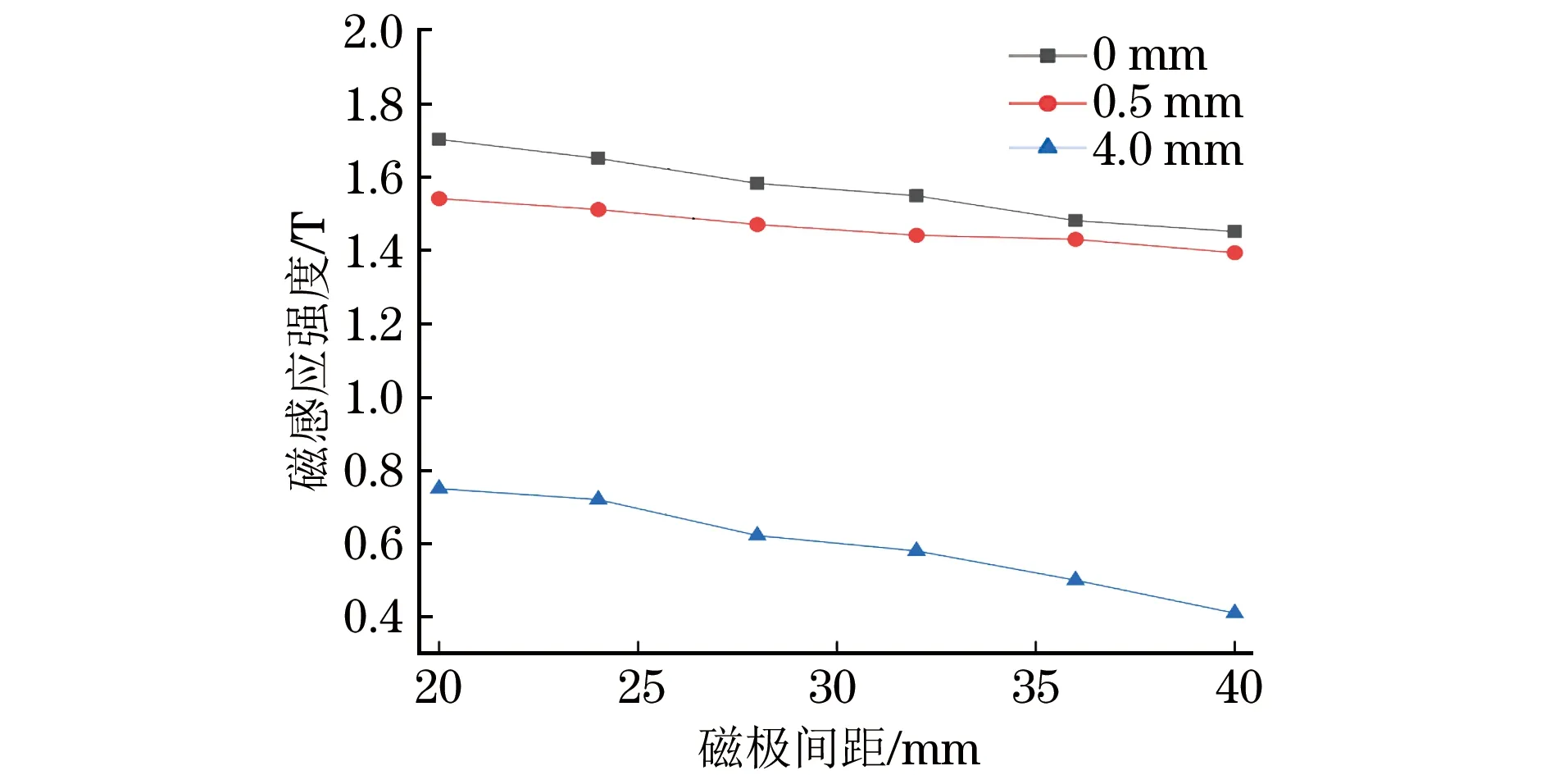
图8 不同分析点的磁感应强度随磁极间距的变化趋势(2#～6#磁轭)

由图8可以看出，在趋肤效应的影响下，随着分析点所处位置深度的增加，Q235钢试样的磁化效果在减弱。但同一深度下，随着磁轭磁极间距的缩短，Q235钢试样分析点处的磁感应强度逐渐增强，试样的磁化效果也就越好。这是因为由硅钢片叠加而成的磁轭的磁导率大于Q235钢试样的磁导率，所以随着磁极间距的缩短，导磁回路中Q235钢的磁路在减小，在总磁路不变的情况下，磁阻在相应减小，所以试样的磁化强度增大。

2.2 不同磁极厚度的仿真结果分析

当磁轭的磁路和磁极间距相同时，磁极的厚度决定了磁轭与试样接触面积的大小，而不同的接触面积也会影响到试样的磁化强度的大小。因此根据上一节的研究结果，选取磁化效果最好，磁极间距为20 mm的6#磁轭作为研究对象，来分析磁极厚度的变化对Q235钢试样磁化强度的影响。不同厚度磁轭的尺寸参数如表3所示。

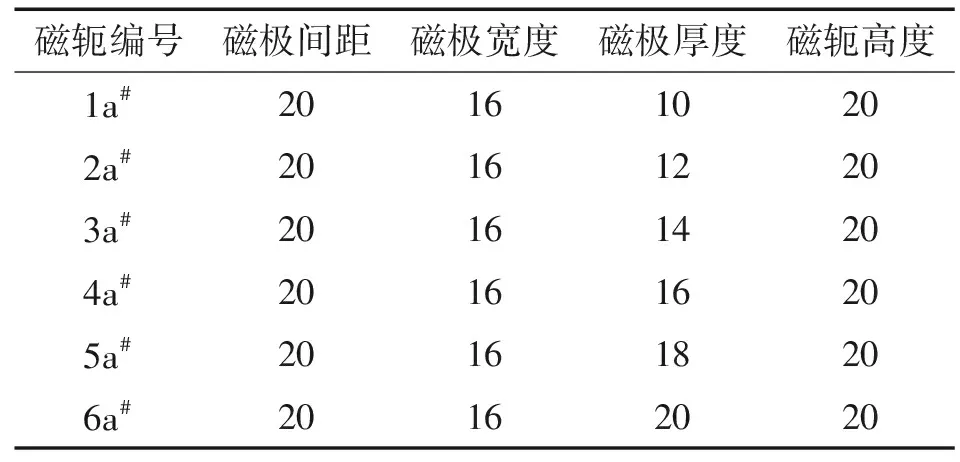
表3 不同厚度磁轭的尺寸参数 mm

用同样的方法在Q235钢试样中心位置(表面0 mm，近表面0.5 mm和中心深度为4 mm处)取3个分析点，然后提取出每组磁轭最大的磁感应强度，做出如图9所示的变化示意图。

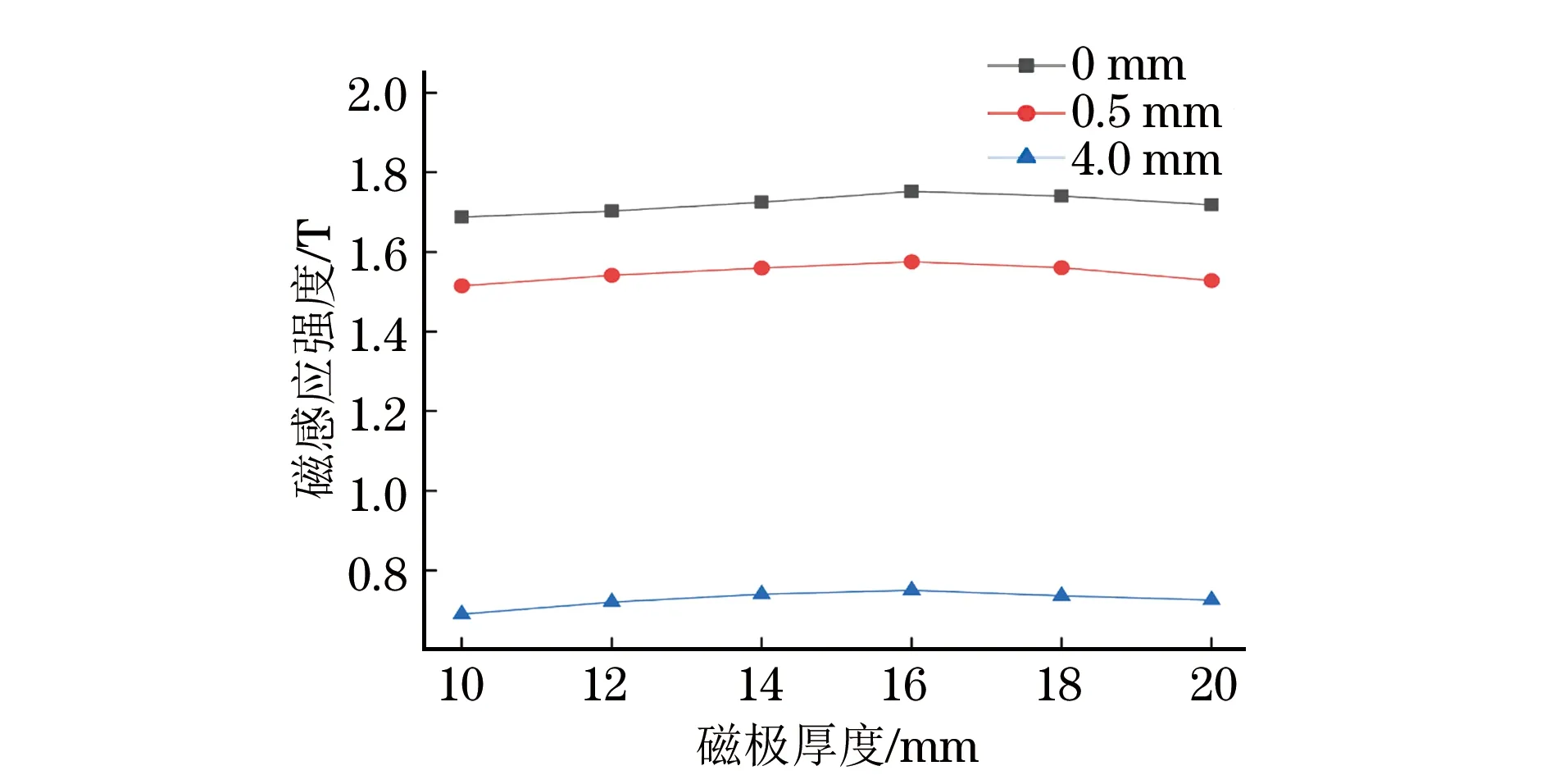
图9 不同分析点的磁感应强度随磁极厚度的变化趋势

从图9中可以观察到，随着分析点深度的增加，Q235钢试样的磁感应强度在减小，磁化效果减弱。同一深度处试样磁感应强度的大小随着磁极厚度的增大呈现出先变大后降低的趋势。通过计算分析点深度为0，0.5,4 mm下的最大和最小磁感应强度的变化率(分别约为3.8%，4.0%，8.7%)，可知磁极厚度的变化对磁轭的磁化效果存在一定的影响，且在磁极厚度为16 mm时达到了最大。

因此磁极间距为20 mm，厚度为16 mm的4a#磁轭励磁时，Q235钢试样的磁感应强度最大，磁化效果也最好。

2.3 不同线圈横截面积的仿真结果分析

为了分析当磁轭两磁极间的间距和厚度确定后，不同线圈的缠绕方式对整个Q235钢试样的励磁强度的影响，选取磁化能力最强的4a#磁轭，线圈的线径保持0.5 mm不变，使线圈尺寸发生变化进行仿真。图10为6组线圈的尺寸示意(图中d为线圈长度，δ为线圈厚度)，表4为线圈尺寸参数。除了第3组的线圈匝数为862匝外，其余5组均为864匝。

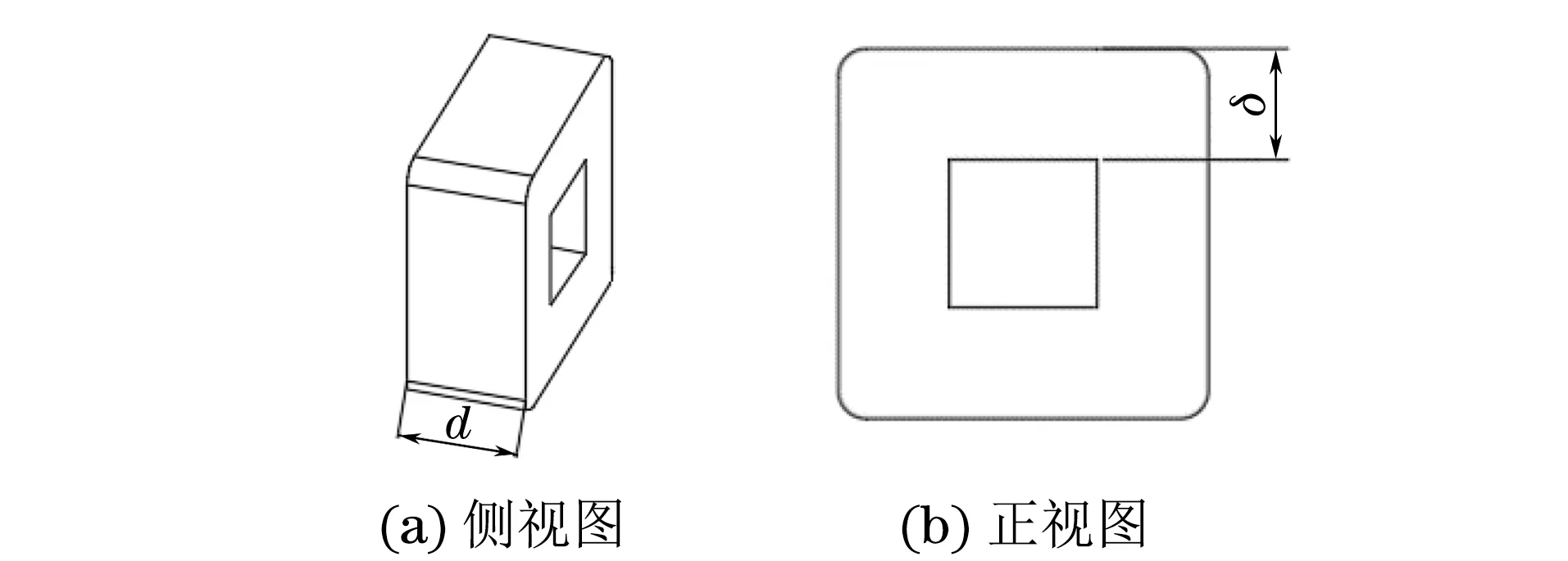
图10 线圈的尺寸示意

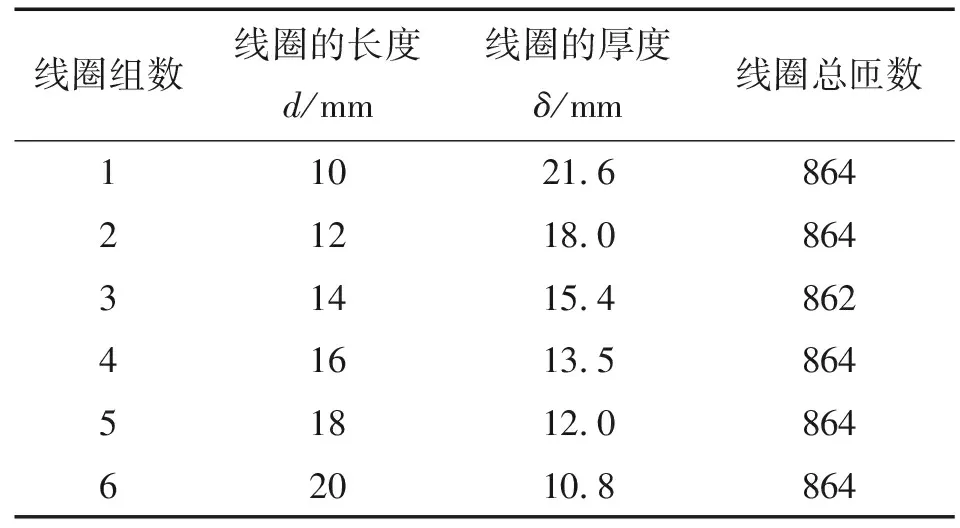
表4 不同线圈的尺寸参数

接着在Q235中心位置(表面0 mm，近表面0.5 mm 和中心深度为4 mm处)取3个分析点，分析瞬态磁场变化时，这3个点处的磁感应强度大小，然后提取出每组磁轭最大的磁感应强度。图11所示为各位置点磁感应强度随线圈尺寸变化示意。

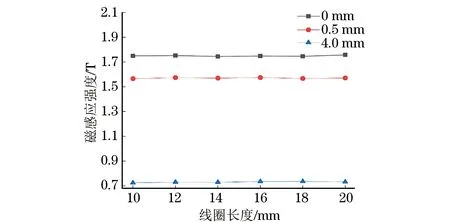
图11 不同分析点的磁感应强度随线圈尺寸的变化趋势

从图11的变化趋势可以看出：同一深度下随着线圈长度的变化，试样的磁感应强度也随之波动，但整体的变化不大。同时计算得到分析点深度分别为0，0.5,4 mm时的最大和最小磁感应强度的变化率约为0.7%，0.5%，0.5%。因此，不同的缠绕方式对整个导磁回路以及Q235钢试样的励磁强度的影响基本不大。试验时为了保证线圈的排列紧密与绕行一致，可以将线圈缠绕在U型磁轭的上端。

综合可知，在上述励磁条件下，磁极间距为20 mm，厚度为16 mm，线圈缠绕在上端时，磁轭的磁化能力最强。

3 结论

利用大型电磁场有限元仿真软件，研究了磁轭磁极间距、厚度以及线圈的缠绕方式对试样磁化效果的影响，找出了磁化效果最好的磁轭尺寸和线圈的缠绕方式，得出以下结论。

(1) 在磁路不变的情况下，同一深度下磁极间距越小，产生的磁场强度越强，Q235钢试样磁化效果越好。

(2) 随着磁极厚度的增大，励磁电流的减小，同一深度分析点处的磁感应强度呈先增大后减小的趋势。

(3) 同样匝数的情况下，线圈的缠绕方式不同，Q235钢试样产生的磁感应强度大小基本保持一致，无明显波动情况。

(4) 选择磁极间距为20 mm，厚度为16 mm，线圈缠绕在上端时，磁轭的磁化能力最强。

以上仿真结果可以为MAE磁化装置的设计提供参考，对提高MAE系统的励磁能力具有明显的意义。