基于STM32的果实收获机械臂运动控制系统研究

刘卓远,李林升

(1.南华大学 机械工程学院，湖南 衡阳 421001；2.上海电机学院 电气学院，上海 201306)

0 引言

在农业现代化的过程中，农业机器人是必不可少的推动者，因此对农业机器人的研究已经成为农业领域的最大研究热点。果实收获机器人作为实现农业自动化的一种设备，实现对其机械臂的精准调控是重点，也是提高生产效率、改善产品品质的一种方式[1]。

针对机械臂的精准调控,人们进行了大量的研究，当下研究较多的有以卡尔曼滤波反馈调节的机械臂模型，以DSP为控制器设计控制系统；其次就是用单片机控制电机和舵机驱动电路,完成机械臂的抓取过程；还有一种基于微机控制的机械臂控制系统。上述方法都能较好地实现对机械臂的运动控制，但是运动精度和响应效率不是那么理想[2]。

针对以上分析,本文选用意法半导体公司的STM32F103作为主控制器，关节姿态信息检测器选用陀螺仪传感器，关节的运动控制采用舵机驱动模块，以上三部分构成了机械臂运动单元的硬件控制系统[3]。机械臂运动单元的软件部分采用KeiluVision4，将陀螺仪采集的关节状态参数作为反馈参数，传递给运动控制模块，进行预估机械臂的运动状态，实现对机械臂运动过程中的偏差调控,这样从硬件和软件两个方面保证了机械臂控制系统的闭环控制。

1机械臂正运动学分析

D-H参数是一个用四个参数表达两对关节连杆之间位置角度关系的机械臂数学模型和坐标系确定系统。它通过限制原点位置和X轴的方向，人为减少了两个自由度，因此它只需要用四个参数即可表达关节之间原本是六自由度的坐标变换[4]。

确定坐标系，对于每个关节都必须指定一个Z轴和X轴。指定Z轴，如果关节是旋转的，则Z轴位于按右手规则旋转的方向。绕Z轴的旋转角是关节的变量；如果关节是滑动关节，则Z轴为沿直线运动的方向。沿Z轴的连杆长度d是关节变量。

指定X轴，当两关节不平行或相交时，Z轴通常是斜线，但总有一条距离最短的公垂线，它正交于任意两条斜线。在公垂线方向上定义本地参考坐标系的轴。如果an表示Zn-1之间的公垂线，则Xn的方向将沿an。

当然也有特殊情况。当两关节的Z轴平行，就会有无数条公垂线。此时可挑选与前一关节的公垂线共线的一条，可简化模型；两关节相交，它们之间没有垂线，这时可将垂直于两条轴线构成的平面的直线定义为X轴，可简化模型。

给每个关节都附上对应坐标系之后，如图1所示。

确定好坐标系后，可以用更简洁的方法来表示D-H四个参数：

Link length(连杆长度)ai-1：沿Xi-1的Zi-1到Zi的距离。

Link twist(连杆扭转)αi-1：Zi相对于Zi-1绕Xi-1旋转的角度。

Link offset(连杆偏移)di：沿Zi的Xi-1到Xi的距离。

Joint angle(关节转角)θi：Xi相对于Xi-1绕Zi旋转的角度。

接下来写出机械臂的D-H参数表，如表1所示。

表1 D-H参数表

根据公式：

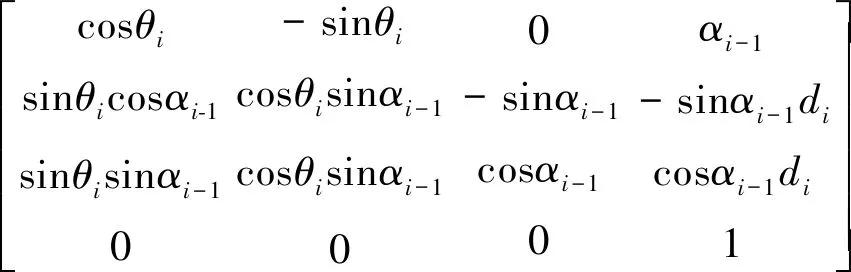
(1)

依次计算每个关节，最后得到机械臂的正运动学公式：

(2)

得到各关节的旋转矩阵后即可根据下面公式得到末端的坐标：

(3)

2 机械臂逆运动学分析

逆运动学是决定要达成所需要的姿势所要设置的关节可活动对象的参数的过程。对于机械臂而言，就是给出夹持器的位置和朝向后求每个关节的旋转角度。为了简化模型，去掉下方云台的旋转关节，这样就可以在二维的平面上进行运动学分析[5]。进行逆运动学分析要进行大量的矩阵运算，先使用几何法对机械臂进行分析，如图2所示。

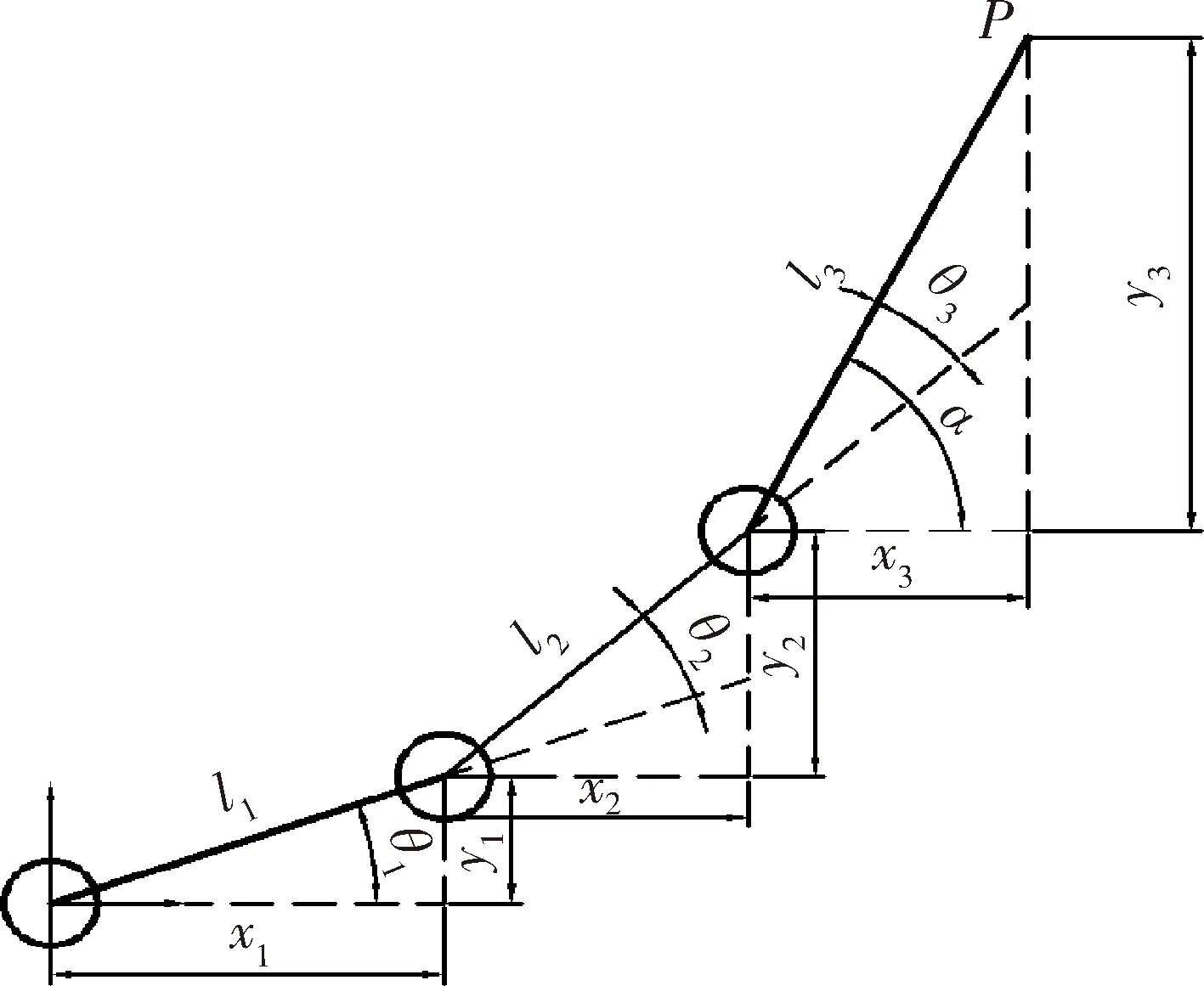
图2 机械臂几何分析示意图

从图2知机械臂的端点P的坐标(x,y),最终由三个部分组成(x1+x2+x3,y1+y2+y3)。其中图中的θ1，θ2，θ3就是要求解的舵机的角度。α是爪子与水平面的夹角。从图上看，显然α=θ1+θ2+θ3。

据此可以列出下式：

(4)

其中x、y为目标物所在坐标，l1、l2、l3为机械臂的机械结构固有属性。

为了方便计算，将已知部分处理一下，作整体考虑：

(5)

将m、n代入已有方程，再化简可得：

l2=(l1cosθ1+m)2+(l0sinθ1+n)2

(6)

通过计算可得：

(7)

上式是一元二次方程的求根公式的形式，其中

(8)

据此求出θ1，同理求出θ2。如此便可求出三个舵机的角度，然后根据角度控制舵机即可实现坐标位置的控制。

输入目标位置的x，y坐标和爪子的俯仰角度，即可计算出目标的舵机角度并转到对应角度上去。

3 机械臂运动控制

为了验证上述分析的正确性，将使用LeArm开源机械手臂进行运动控制实验。先使用基于PC+STM32运动控制模块的方法，需要将两者通过串口联接，这个串口用来与电脑上位机通信。

初始化串口，将串口配置为波特率115 200 b/s、8位数据位、1位停止位、无校验位。另外用两个IO口来控制单线串口的收发状态，发送的指令需要舵机返回数据，在发送了指令之后将单线串口设为接收状态。根据接收到的指令做出对应的操作，如图3所示。

发送使用轮询寄存器方法实现，接收使用接收中断。先让舵机转动，单片机本身具备单线串口通信的功能,STM32上的串口自身可以支持单线通信，底板上设计有两线串口转为单线串口的电路。

使用逻辑电路可以简化程序代码，同时提高代码的通用性。和普通的串口通信一样使用串口，按照通信协议即可控制总线舵机。函数组织好指令之后，调用UART_TX_ENABLE将单线串口设为发送模式，然后调用发送函数将数据发送出去，这样就能实现机械臂的运动控制[6]。机械臂运动控制系统设计的流程如图4所示。

图4 PC+STM32控制模块的实验框图

4 仿真与结论

本文研究LeArm开源机械手臂，整体结构如图5所示。

图5 LeArm开源机械手臂

该机器臂为满足pieper准则的6—DOF机器臂，为了研究其位置控制，实验仿真只针对其关节2与关节3进行研究[7]。该机器人采用改进的D-H参数进行标识，建模之后的结构如图6所示。

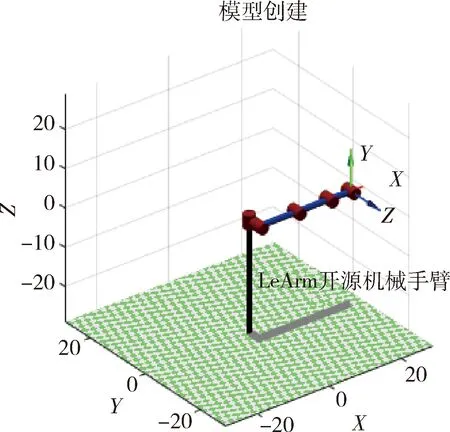
图6 LeArm开源机械手臂模型图

通过实验选择定义机械臂的起始点、中间点、终止点坐标，仿真得出其对应的初始点位姿、中间点位姿与末端点位姿，如表2所示。

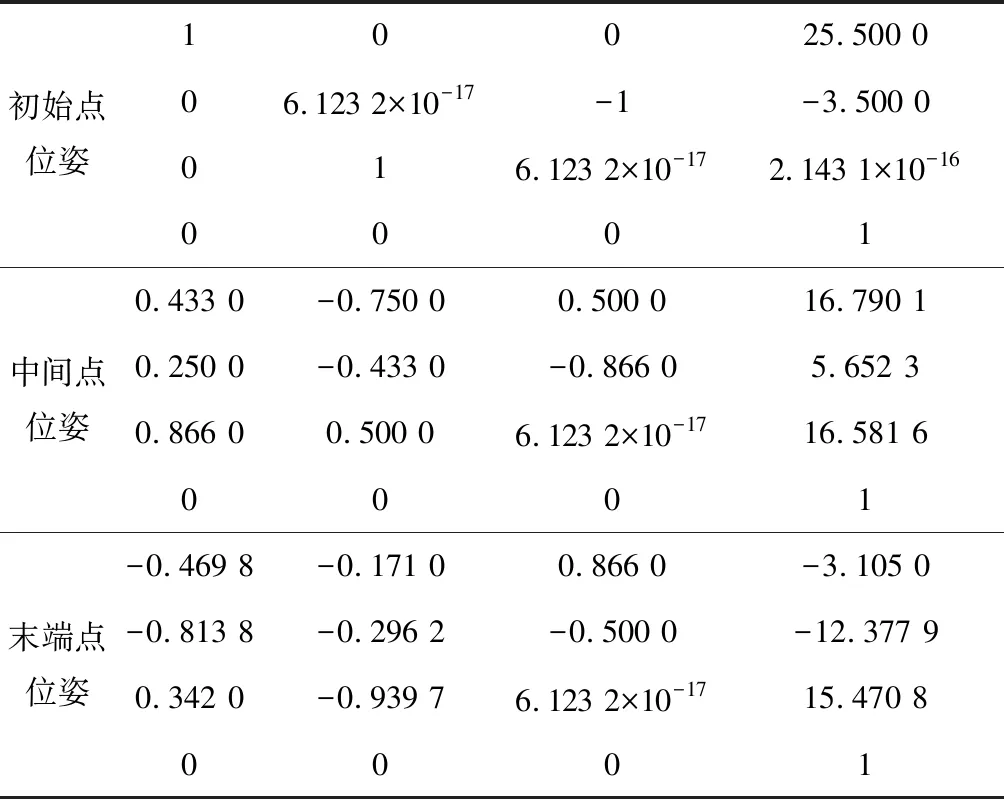
表2 位姿点4×4矩阵表

由于该机器人满足pieper准则，因此其逆解可以采用代数法进行求解，其逆运动学采用代数法对其进行求解[8]。在笛卡尔坐标系下给定机器人的末端位姿的轨迹图，如图7所示。

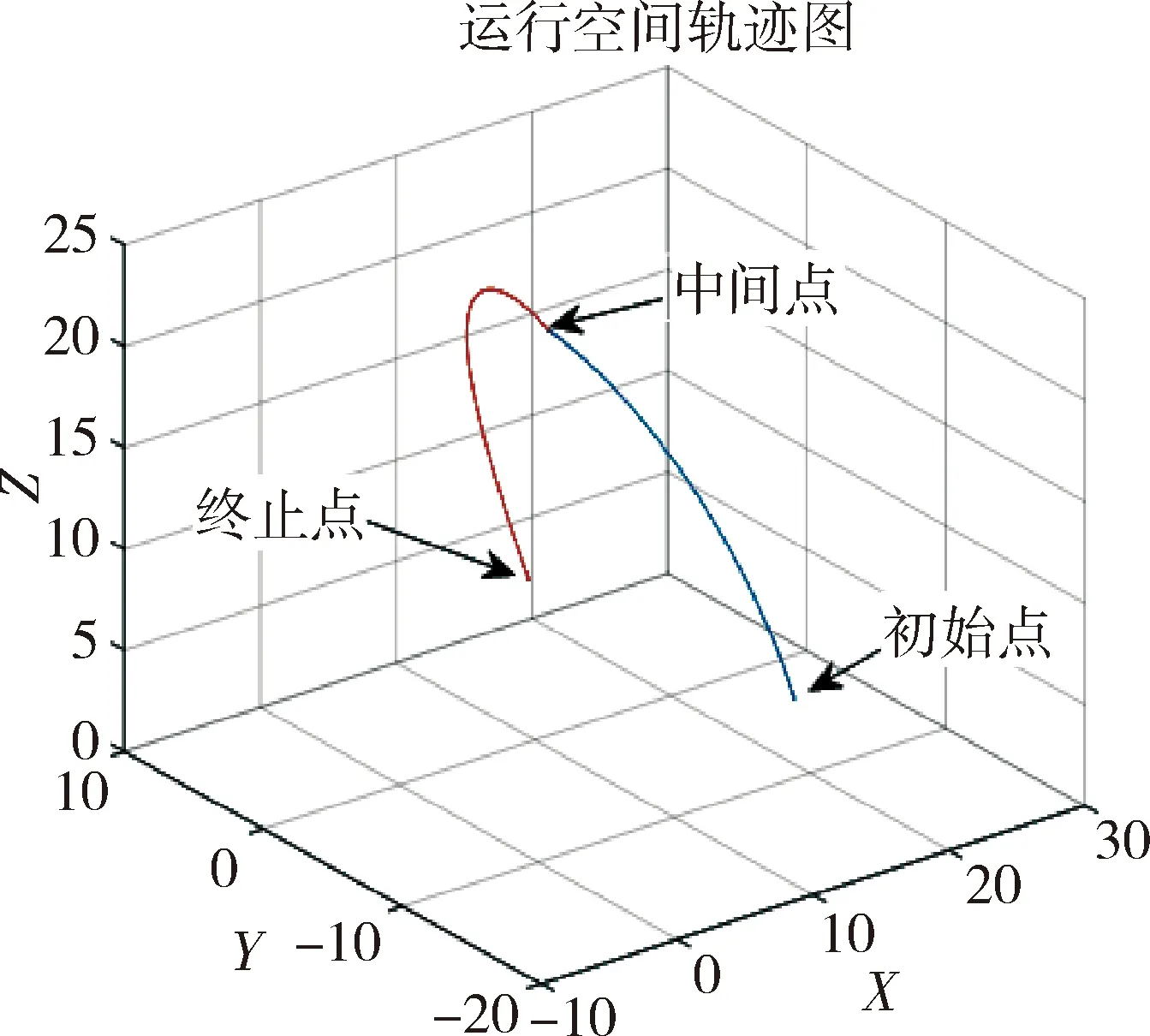
图7 笛卡尔坐标系下给定机器人的位姿的轨迹图

由以上仿真结果分析可得，采用改进后的轨迹规划方法能够缩短整个机械臂的运行时间，并且能够保证规划出来的位移、速度、加速度曲线在整个运动过程中的连续性和平滑性在一个较理想的范围内，从而使得在缩短时间的前提下还能继续保证整个机械臂的稳定运行。