基于灰关联分析法和多元线性回归模型的有轨电车能耗预测
苏兆路,潘春阳
(中交隧道局电气化工程有限公司,北京 100102)
0 引言
随着国民经济的高速发展,城市居民私家车的保有量急剧增长,小汽车给人们带来便捷的同时,也引起了越来越严重的城市问题,比如:交通拥堵、能源紧缺、环境污染、土地资源不足等。而地铁、轻轨、有轨电车等大容量城市轨道交通因为运量大、单位能耗小、环保、占用土地资源少等优势在国内外得到大力发展[1-2]。相对地铁和轻轨,有轨电车兼顾了运量较大、单位能耗较小、绿色环保、建设成本较低和建设周期较短等优势,使其近年来在国内一些大中城市发展迅速[3]。然而,有轨电车作为大容量的城市轨道交通,由于运量大和发车间隔小,使得其总能耗比较大,是城市的用电大户。为了给运营部门在系统节能潜力估计时提供一个较为准确的参考,有轨电车系统能耗预测显得十分重要。
近年来国内外学者对城市轨道交通能耗预测进行了研究,其中文献[4]通过对车辆受力分析建立有轨电车的牵引能耗模型,然后对车辆能耗进行仿真计算;文献[5]通过分析有轨电车车辆充放电特性,建立了有轨电车能量传输模型,实现对有轨电车牵引能耗的估计;文献[6]根据铁路电力机车的运动过程分析车辆能耗影响因素的灵敏度,进而分析各因素对车辆能耗的影响;文献[7]基于实际交通数据开发有轨电车能源消耗模型,模拟车辆能源消耗过程;文献[8]首先确定有轨电车系统能耗影响因素,然后利用多元线性回归模型预测有轨电车系统能耗;文献[9]利用指标法建立能耗评价指标,对城市轨道交通中远期能耗进行预测。综上所述,目前对城市轨道交通能耗预测的研究大致有牵引能耗仿真计算、回归分析法和指标法三类。牵引能耗仿真计算需建立复杂的数学模型,不易实现;指标法需要确定大量参数,且一般适用于中长期能耗预测。灰关联分析法不需要考虑样本量的多少和样本有无典型分布规律,克服了传统多元回归分析的不足,特别是对于一些历史数据记录少,统计数据灰度较大,要挖掘影响系统行为特征的主要因素,该方法行之有效,同时减少了挑选变量分析计算工作的时间。基于灰关联分析的多元线性回归模型,能够把影响系统发展的主要因素结合起来预测系统未来的发展趋势。因此本文提出灰关联和回归模型相结合的有轨电车能耗预测方法。通过灰关联分析对有轨电车系统能耗影响因素的影响程度进行量化,选取其中对系统能耗影响较大的因素作为模型的输入变量,利用多元线性回归模型建立有轨电车能耗模型,然后以2017年广州海珠有轨电车能耗数据为依据,对模型的准确性进行验证。
1 有轨电车能耗影响因素
1.1 有轨电车系统能耗构成
有轨电车系统能耗包括车辆运行能耗和动力照明能耗。其能耗构成如图1所示。
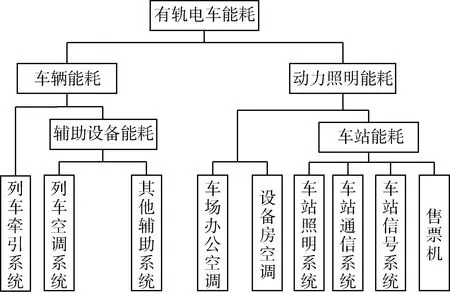
图1 有轨电车系统能耗构成
1.2 有轨电车能耗影响因素分析
有轨电车系统不同于地铁等其他城市轨道交通系统,车站配置简单,系统主要能耗为车辆能耗。因此,本文对有轨电车车辆能耗影响因素进行分析。
1.2.1 牵引能耗影响因素分析
有轨电车在站间运行时,车载超级电容器系统需要提供车辆克服启动阻力、基本运行阻力和附加阻力的能耗,同时超级电容器还需提供车辆动能增加所需的能耗,附加阻力只在特殊运行情况下产生,这里不做考虑。根据车辆的动力学模型[10-12]可得:
(1) 车辆克服启动阻力的能耗:
(1)
其中,f0为车辆启动阻力,m为车辆总重,g为重力加速度,E1为车辆克服启动阻力的能耗,S0为启动过程车辆运行距离。
(2) 车辆克服基本阻力的能耗:
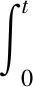
(2)
其中,fj为车辆所受基本阻力,a、b、c为阻力系数,v为车辆运行速度,E2为车辆克服基本阻力的能耗。
(3) 车辆动能增加所需的能耗:
(3)
其中,E3为车辆动能增加所需能耗,m为车辆总重,v为车辆运行速度;
(4) 车辆牵引能耗:
(4)
其中,Eq为车辆牵引能耗,η为有轨电车电机的转换效率。
通过对有轨电车运动过程分析并结合式(1)~(4)可知,有轨电车牵引能耗由车辆总重、车辆运行速度、车辆所受基本阻力、车辆行驶距离和有轨电车电机转换效率等因素决定。车辆总重因载客量的不同而不同,车辆所受基本阻力由线路条件和列车运行速度决定。对于指定的线路和车辆型号,阻力系数、车辆自重和车辆电机转换效率是定值,它们对有轨电车牵引能耗的影响一般是固定的。因此,变化的影响因素为客运量、运营里程和运行速度。此外,由于路口红绿灯情况会影响车辆的启停次数,因此其对有轨电车牵引能耗也有一定影响。路口红绿灯情况对车辆能耗的影响可通过绿灯通过率来表征。综上所述,影响有轨电车牵引能耗的因素中可量化分析且变化的因素有客运量、运营里程、车辆运行速度和绿灯通过率。
1.2.2 辅助设备能耗影响因素分析
有轨电车辅助设备能耗主要为车辆空调系统能耗。通常情况下,车辆空调系统的能耗高低是由车内环境温度决定的[13]。因此,客运量、环境温度是影响车辆辅助设备能耗的因素。另外由于路口红绿灯情况会影响车辆在区间的运行时间,因此其对车辆辅助设备能耗也会有一定影响,绿灯通过率计算公式如下:
(5)
其中,Pg为车辆绿灯通过率,N为车辆通过的路口的总数量,Ng为车辆绿灯通过的路口数量。
2 能耗分析模型
2.1 灰关联分析
灰色系统理论是由邓聚龙教授提出的一种研究少信息问题的新方法,灰色关联分析是其重要分支,其基本思想是根据研究对象曲线之间的相似度来判断不同对象的联系是否紧密[14]。该方法可弥补主成分分析、方差分析要求数据量大、要求样本服从某一典型的概率分布、要求各因素之间彼此无关、计算量较大等不足。灰色关联模型如下:
(1)根据评价体系确定反映系统变化的特征序列,然后统计该特征序列构成:
X0=(x0(1),x0(2),…,x0(n))
(6)
(2)分析影响系统发展的系统灰色关联因素,然后统计这些因素序列构成:
Xi=(xi(1),xi(2),…,xi(n)),i=1,2,…,m
(7)
(3)利用D1对特征序列X0和因素序列X1进行无量纲处理:
XiD1=(xi(1)d1,xi(2)d1,…,xi(n)d1)
(8)
其中,xi(k)d1=xi(k)/xi(1);xi(1)≠0;k=1,2,…,n;D1为初值化算子。
(4)计算X0与Xi的关联系数和关联度;
Δmin=min|x0(k)-xi(k)|
(9)
Δmax=max|x0(k)-xi(k)|
(10)
(11)
(12)
其中,γ(x0(k),xi(k))为k点关联系数,γ(X0,Xi)为X0和Xi的邓式关联度,ρ为分辨系数,通常情况下取0.5[14]。
(5)比较各因素的关联度大小,找出影响系统发展的显著因素。
2.2 多元线性回归模型
2.2.1 回归模型
如果两个或两个以上自变量与因变量之间存在线性关系,对多个自变量与因变量之间进行的回归分析即为多元线性回归[15]。多元线性回归的数学模型如下:
y=a0+a1x1+a2x2+…+anxn+ε
(13)
其中a0,a1,a2,…,an为回归系数,ε为随机误差或其他因素引起的y的线性变化部分。
2.2.2 模型显著性分析
回归模型确定后需要对其显著性进行检验,对于多元线性回归模型通常需要F检验和t检验,其中,F检验确定因变量和自变量之间的线性关系是否总体显著,t检验确定每一个自变量和因变量是否都显著[15]。
(1)F检验
(14)
其中,SSR是回归平方和,SSE为剩余平方和,p和n-p-1分别为SSR和SSE的自由度。
(2)t检验
(15)
其中,Z为SSE的自由度。
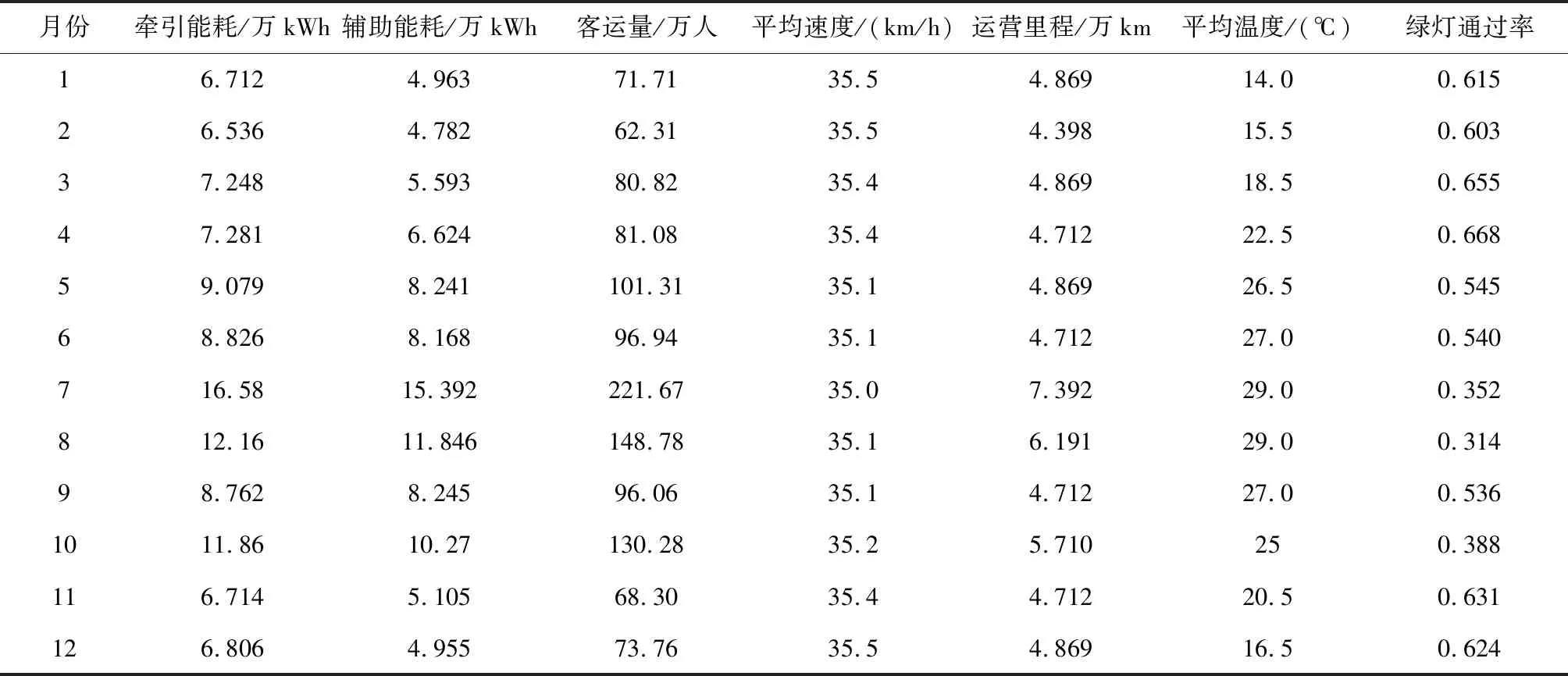
假设H0:a0,a1,a2,…,an=0成立,通过确定显著性水平α的值确定显著性临界值Fα(p,n-p-1)和tα/2(n-p-1),如果F>Fα(p,n-p-1)和t>tα/2(n-p-1)同时成立,则假设H0不成立,表示模型的回归效果比较可靠;如果F 经调研和统计得到广州海珠有轨电车2016年车辆牵引能耗、车辆辅助能耗和其他可获得的数据统计如表1所示。 表1 车辆能耗及其他可获得的数据 通过分析表1中数据可知,2016年7、8月份的牵引能耗和辅助能耗是全年中最大的,其对应的运营里程、客运量和月平均温度均大于其他月份。此外,10月份由于十一假期的缘故导致其客运量比较大,牵引能耗和辅助能耗也较大。总体来看,牵引能耗的变化趋势和运营里程、客运量、绿灯通过率的变化趋势相似,辅助能耗的变化趋势和月均温度、客运量、绿灯通过率的变化趋势相似,车辆平均速度变化趋势与车辆牵引能耗的变化趋势相似度不太明显,这些因素与能耗的关联度大小还需计算。下面通过灰关联模型具体分析这些因素与牵引能耗和辅助能耗的关联度大小: (1) 有轨电车牵引能耗构成行为序列X0,客运量、平均速度、运营里程、绿灯通过率分别构成因素序列X1,X2,X3,X4。 (16) (2) 根据式(8)对X0,X1,X2,X3,X4进行无量纲处理,然后由式(9)~(11)计算X1,X2,X3,X4与X0在每个点的关联系数,最后由式(12)求得客运量、平均速度、运营里程和绿灯通过率对车辆牵引能耗的关联度大小,计算结果如表2所示。同理计算得客运量、平均温度和绿灯通过率对车辆辅助能耗的关联度大小如表3所示。 表2 牵引能耗影响因素关联度 表3 辅助能耗影响因素关联度 根据文献[13]对城市轨道交通能耗影响因素关联度的分析可知,关联度大于0.9的因素为显著影响因素,大于0.7的因素为主要影响因素,大于0.5的因素为一般影响因素,小于0.5的因素为轻微影响因素。结合表2和表3可知对牵引能耗影响较大的因素分别为运营里程、客运量和绿灯通过率,对辅助能耗影响较大的因素分别为平均温度、客运量和绿灯通过率。因此,可选取这些因素作为能耗模型的输入量。 根据文献[8]、[13]对城市轨道交通能耗数据的研究可知,系统能耗与能耗影响因素之间存在显著的线性关系。因此,利用多元线性回归模型对有轨电车系统能耗建模。文献[8]中确定的有轨电车车辆牵引能耗影响因素为运营里程和客运量,车辆辅助能耗影响因素为平均温度和客运量,分别以文献[8]中确定的模型输入量和本文确定的模型输入量建立传统能耗模型和改进能耗模型,根据式(13)建立的模型如下: 传统模型: (17) 改进模型: (18) 根据表1中2016年广州海珠有轨电车车辆牵引能耗和辅助能耗及相关数据运用回归拟合确定有轨电车牵引能耗模型和辅助能耗模型的模型参数。 根据式(14)、(15)对两种模型进行检验,检验结果如表4所示。 表4 模型显著性检验结果 在显著性水平α=0.05时,经查表可知,传统模型和改进模型的Fα(p,n-p-1)值分别为4.26和4.07,tα/2(n-p-1)值分别为2.26和2.31。通过对比表4可知,两中模型下求得的F值和t值均大于临界值,因此,两种模型在显著性水平α=0.05情况下均显著。 经调研和统计得广州海珠有轨电车线路2017年车辆牵引能耗、辅助能耗、客运量、运营里程、平均温度和绿灯通过率数据如表5所示。在2016年能耗数据的基础上,分别根据传统模型和本文新建模型对广州海珠有轨电车2017年有轨电车车辆牵引能耗和车辆辅助能耗进行预测,两种模型的预测结果如表6所示。 表5 车辆能耗及其他可获得的数据 表6 模型预测结果 由表5中能耗实际值和表6中能耗的预测值绘制牵引能耗、辅助能耗和总能耗的误差曲线如图2所示,两种模型的误差统计值如表7所示。 图2 能耗误差曲线 由图2可知,对于车辆牵引能耗、车辆辅助能耗以及车辆总能耗,改进模型的预测误差均小于传统模型。通过表7可知,传统模型的平均误差在4%以上,而改进模型的平均误差大约为2%,因此,改进后的模型可靠性更高。此外,由图2可知改进模型的误差最大值出现在7、8、10三个月,但误差都保持在±5%以内,通过分析可知,7、8两个月由于在暑期,客运量大、平均温度高,10月份由于十一假期的缘故客运量也比较大,因此,由这些因素造成的能耗非线性部分随之增大,从而造成较大的预测误差。总之,改进的模型具有更高的预测精度,能够更好地反映有轨电车车辆能耗与影响因素之间的关系。 本文提出了一种基于灰关联和回归模型相结合的有轨电车能耗预测方法,通过有轨电车的动力学模型分析影响有轨电车能耗的因素,利用灰关联分析法计算这些因素与车辆能耗的关联度,然后选取关联度较大的因素作为回归模型输入量建立有轨电车能耗多元线性回归模型,通过与已有文献中回归模型比较可知,模型中考虑交通灯这一因素后,车辆总能耗的平均预测误差从4.30%降到2.29%,说明新建模型具有更高的准确性。 严格意义上车辆能耗与其影响因素之间是非线性关系,因此,由于非线性部分的影响,本文建立的模型在7、8、10等环境温度高、客运量大的月份预测误差较大,但误差都在5%以内,因此所建立的模型基本能够反映有轨电车的能耗变化的趋势。3 有轨电车能耗建模
3.1 灰关联分析
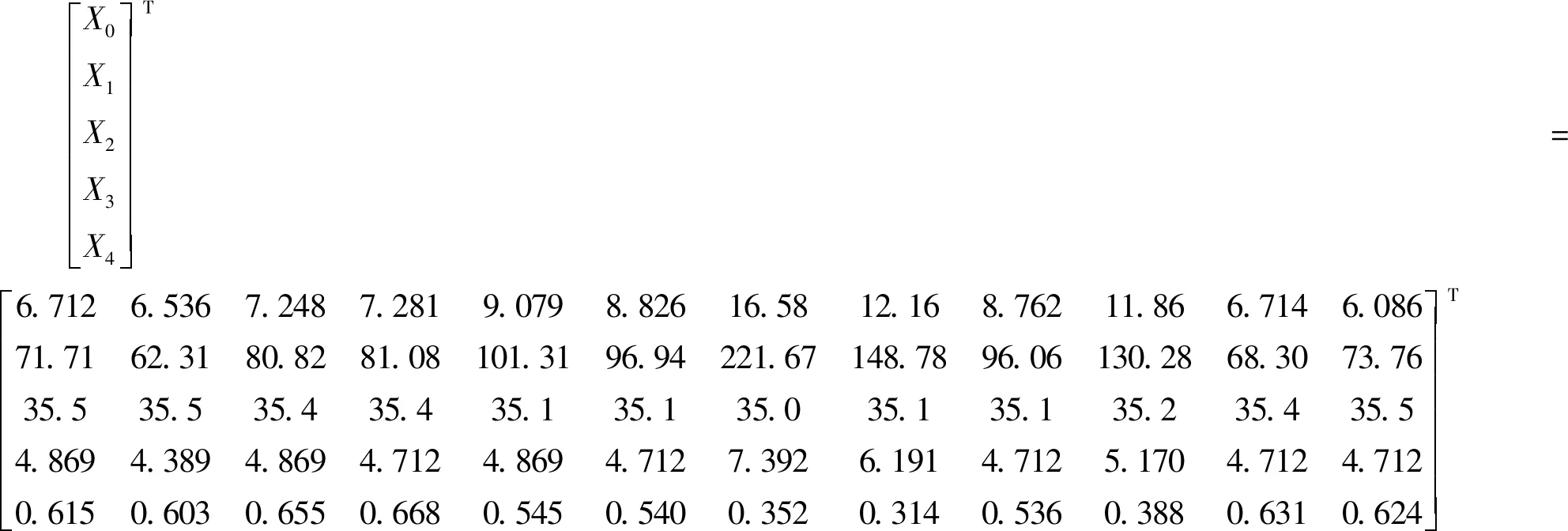


3.2 建立模型
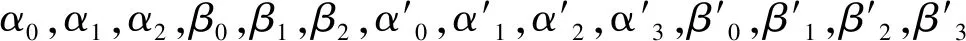
3.3 参数确定和显著性检验
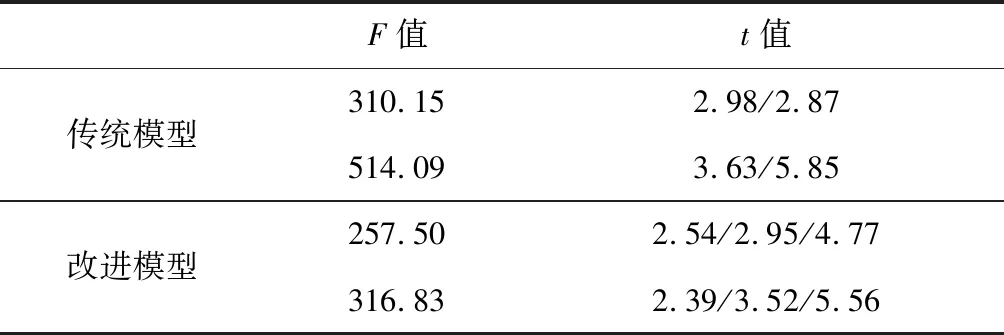
4 实验分析
4.1 能耗预测

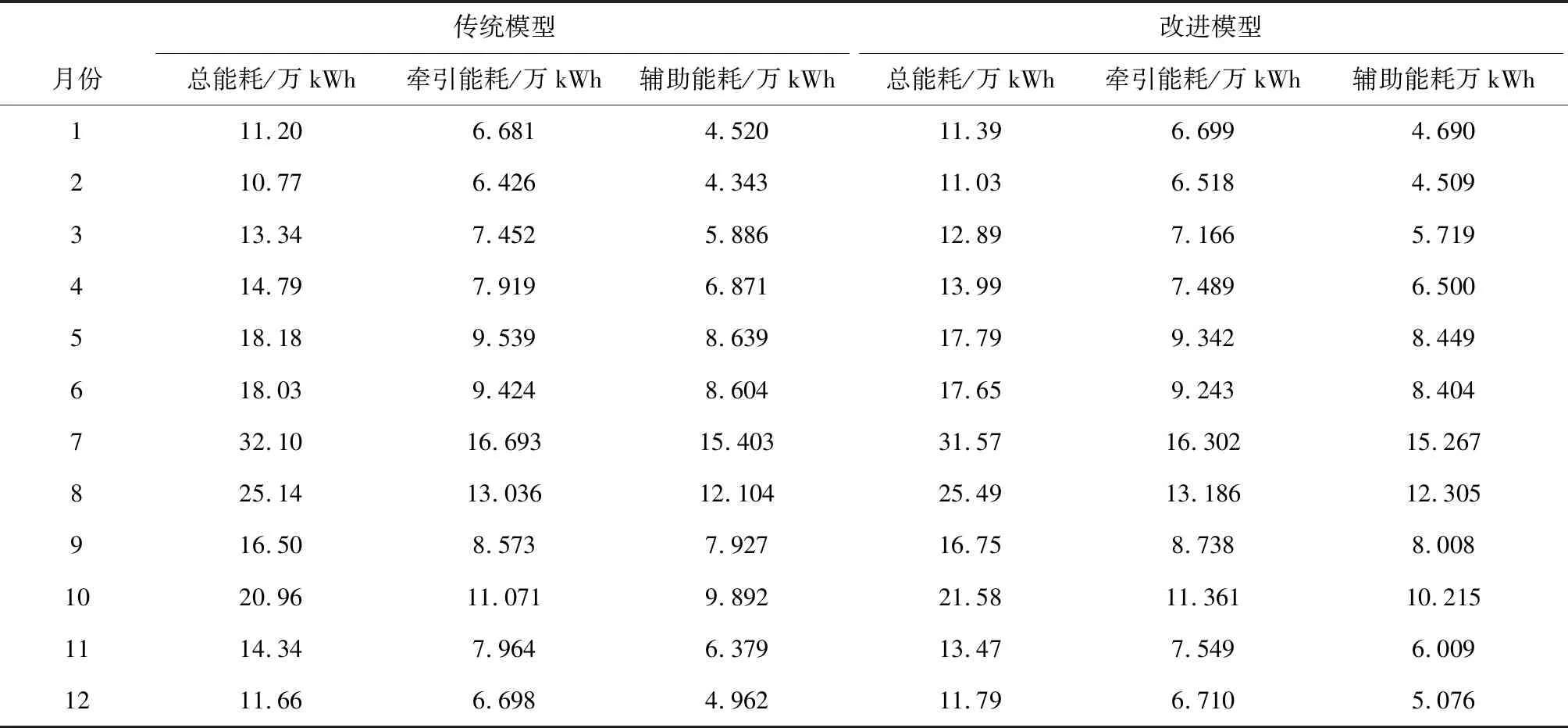
4.2 误差分析
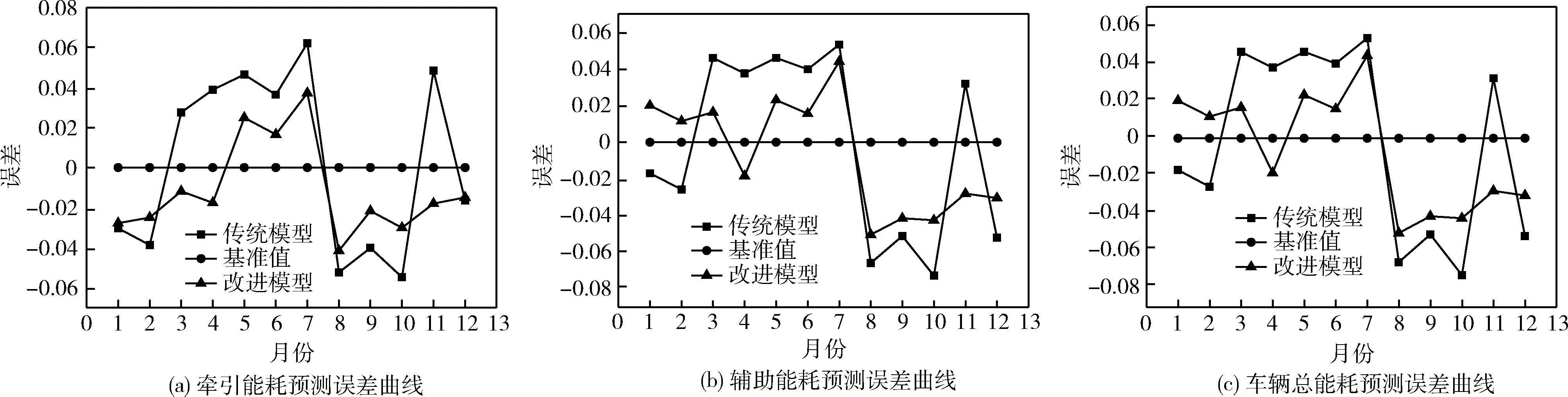
5 结论

