不等厚板低匹配对接接头弯曲承载能力设计

王佳杰 张颖 张敬强 肖雪 孙浩

摘要：为了提高不等厚板低匹配对接接头弯曲承载能力，基于等承载定义、判据和实现条件，通过理论研究结合有限元分析，在弹性极限状态下对不等厚板低匹配对接接头进行了几何形状设计。 理论分析表明，靠近薄板材侧的余高形状可以按照等厚板低匹配对接接头弯曲等承载设计方法进行设计，而靠近厚板材侧的余高形状以圆弧过渡形式进行设计。为了工程上应用的方便，将不等厚板低匹配对接接头设计成新的三圆相切形状。设计的不等厚板低匹配对接接头与相关标准推荐的不等厚板圆弧过渡的等匹配对接接头进行了有限元验证比较。结果表明，按照理论设计的不等厚板低匹配对接接头的弯曲承载能力与不等厚板三圆相切低匹配对接接头相当，均优于不等厚板凹形圆弧过渡等匹配对接接头，但是均略低于不等厚板凸形圆弧过渡等匹配对接接头。不等厚板低匹配对接接头弯曲承载能力设计为完善焊接结构等承载理论与工程应用提供重要的理论支撑。

关键词：不等厚板;低匹配对接接头;弯曲承载能力;几何形状设计;有限元验证

中图分类号：TG 404

Abstract：To improve the bending load-carrying capacity （BLCC） of under-matched butt joints of unequal thickness plates， the geometric shapes is designed through theoretical research with finite element analysis based on the definition， criterion and realization condition of equal load-carrying capacity （ELCC） in elastic stage limit. Theoretical research showed that the reinforcement geometry near the thin sheet side can be designed according to design method of under-matched butt joints of equal thickness plate， nevertheless， the reinforcement geometry near the thick plate side can be designed as the smooth circular arc transition. For the convenience of engineering application， the geometry of under-matched butt joints of unequal thickness plates can be designed as a new three-circle tangential butt joints shape. The under-matched butt joints of unequal thickness plates designed in this paper are verified by finite element method and compared with equal-matched butt joints of unequal thickness plates with circular arc transition recommended by the relevant standards. The results showed that the BLCC of the under-matched butt joints of unequal thickness plates designed according to the theory was equivalent to that of the three-circle tangential butt joints. BLCC of the under-matched butt joints of unequal thickness plates is better than that of the equal-matched butt joints with the concave arc transition， but slightly lower than that of the equal-matched butt joints with the convex arc transition. Design of BLCC for under-matched butt joints of unequal thickness plates can provide important theoretical support for perfecting ELCC theory and engineering application of welded structures.

Key words：unequal thickness plates; under-matched butt joints; BLCC; geometric shapes design; finite element verification

0 前言

隨着工业迅速发展，焊接结构迫切需要向高强度、轻质量、高性能和低成本方向发展，因此通常使用轻质材料、高强钢或者利用结构设计提高结构轻量化。高强度材料应用越来越广泛，但是高强钢焊接冷裂纹、HAZ脆化和软化等问题屡见不鲜[1-5]。采用低强度材料作为熔敷金属可以有效解决高强钢焊接出现的问题[1-3，6]。但是低强匹配的焊接接头承载能力相对较低，为了提高其承载能力，相关研究者从焊接结构设计角度出发，并建立了相应的设计准则和设计方法[7-12]。目前，国内外文献未见关于不等厚板焊接接头弯曲承载能力方面的研究工作，因此文中针对弹性极限状态下不等厚板单面连接低匹配对接接头的弯曲承载能力进行研究，为完善等承载设计理论与工程应用提供技术支撑。

1 标准推荐的不等厚板对接焊

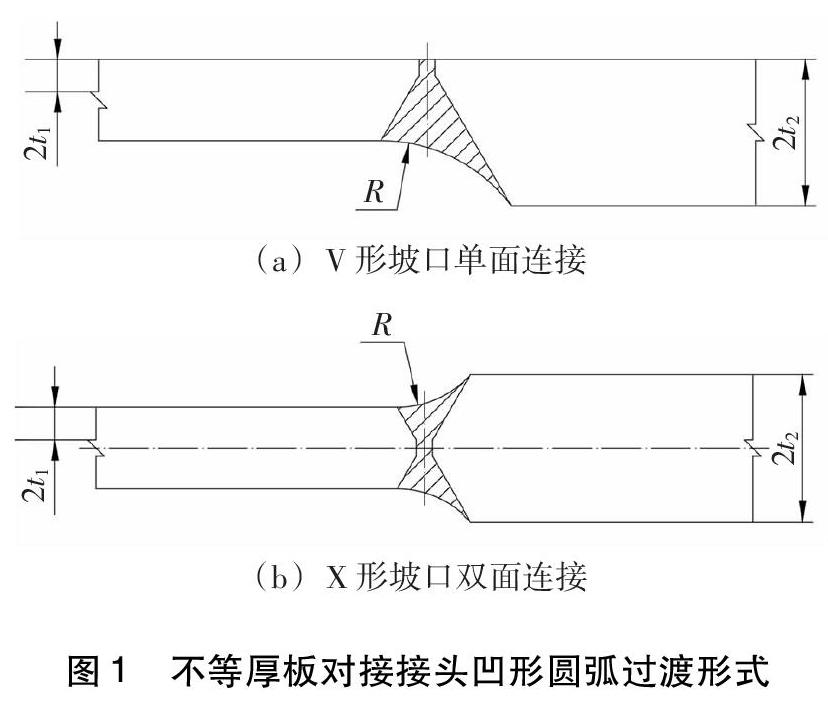
对于不等厚板对接接头，设薄板板厚为2t1，厚板板厚为2t2，厚度差为Δt =2（t2-t1）。按照标准ISO 9692-1-2003《焊接及相关工艺》推荐：对于不等厚板对接焊时，坡口之间可以利用凹形圆弧进行圆滑过渡，如图1所示。如果接头为单面连接，按照图1a方式进行设计与加工;如果接头为双面连接，按照图1b的方式进行设计与加工。

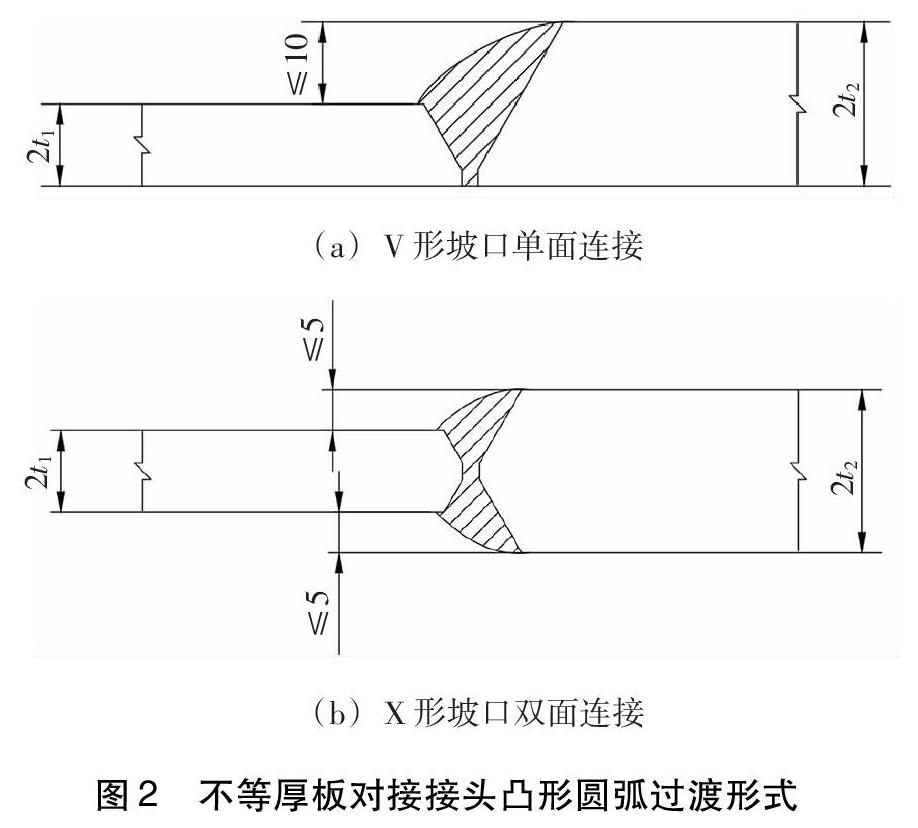
标准DIN 18800-1-2008 《钢结构 第1部分：设计和建造》推荐，对于不等厚板对接接头全熔透焊接，当承受主静载作用时，要求厚度差Δt≤10 mm;当承受动载荷时，要求厚度差Δt≤3 mm。静载条件下不同厚度板对接，如果接头为单面连接，且厚度差Δt≤10 mm，按照图2a方式进行设计与加工;如果接头为双面连接，且单侧厚度差Δt≤ 5 mm，按照图2b方式进行设计与加工。

当两板材厚度差较大时，即Δt≥10 mm时，往往需要将厚板材一侧加工成1∶1或更小过渡斜面。文中针对单面连接的不等厚板低匹配对接接头情况进行研究。

2 不等厚板低匹配接头弯曲等承载设计

以上标准推荐的不等厚板对接接头设计是相对等匹配对接接头而言。毋庸置疑，不等厚板低匹配接头的弯曲承载能力低于母材或等匹配接头。承载能力不仅与构成接头本身的材料性能有关，而且与接头的几何参量有关[2-8]。为了提高不等厚板低匹配接头弯曲等承载能力，可以通过增大不等厚板低匹配接头焊缝每个承载横截面的厚度，并通过接头细节设计降低承载薄弱区的应力集中，从而使不等厚板低匹配接头的弯曲承载能力达到母材或等匹配接头。

根据弯曲等承载设计判据与实现条件，与文献[7，11]给出了等厚板低匹配对接接头满足等承载条件的最低余高设计曲线hmin（x）公式（1）：

式中：以焊缝中心为坐标原点，x为到焊缝中心的距离;l为三点弯曲跨距;μMMR为低匹配接头的屈服强度配比。

当x=0时，为等厚板低匹配对接接头焊缝中心处满足等承载的最低设计余高hmin（0）：

文献[11]给出了等厚板低匹配对接接头满足等承载条件的最小设计熔宽wmin为：

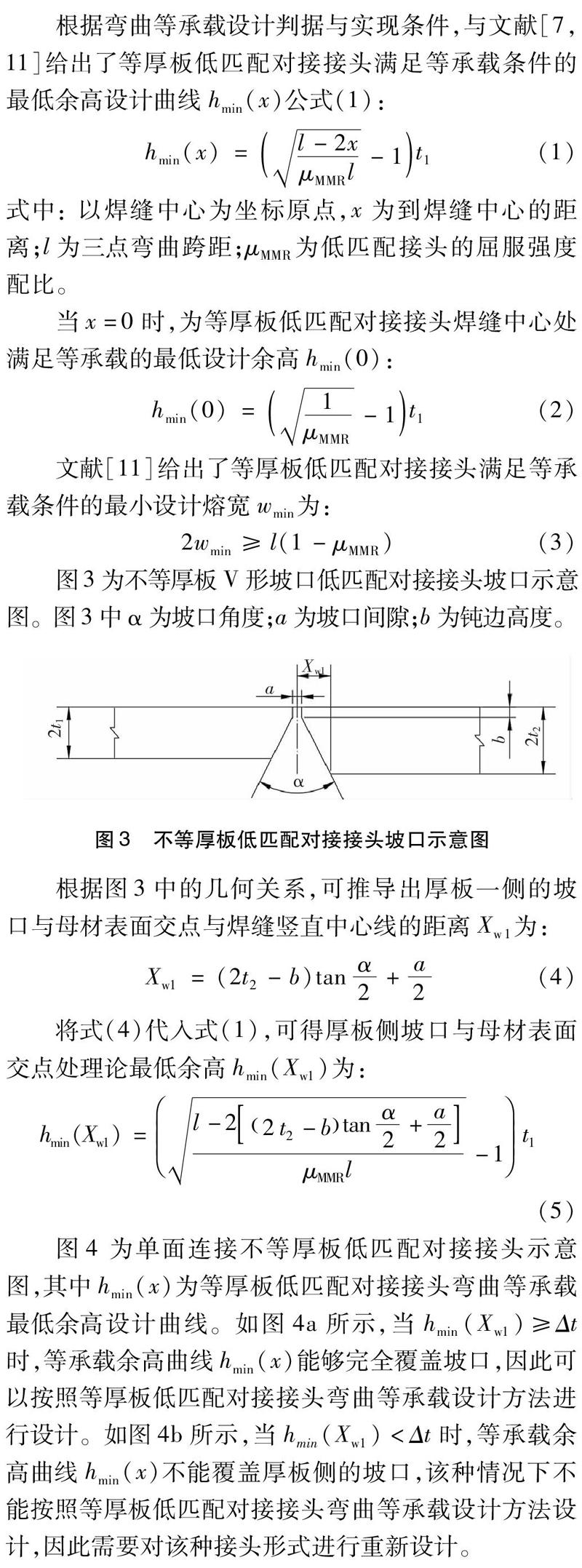
图3为不等厚板V形坡口低匹配对接接头坡口示意图。图3中α为坡口角度;a为坡口间隙;b为钝边高度。

根据图3中的几何关系，可推导出厚板一侧的坡口与母材表面交点与焊缝竖直中心线的距离Xw1为：

将式（4）代入式（1），可得厚板侧坡口与母材表面交点处理论最低余高hmin（Xw1）为：

图4 为单面连接不等厚板低匹配对接接头示意图，其中hmin（x）为等厚板低匹配对接接头弯曲等承载最低余高设计曲线。如图4a所示，当hmin（Xw1）≥Δt时，等承载余高曲线hmin（x）能够完全覆盖坡口，因此可以按照等厚板低匹配对接接头弯曲等承载设计方法进行设计。如图4b所示，当hmin（Xw1）<Δt时，等承载余高曲线hmin（x）不能覆盖厚板侧的坡口，该种情况下不能按照等厚板低匹配对接接头弯曲等承载设计方法设计，因此需要对该种接头形式进行重新设计。

对于焊缝竖直中心线左侧靠近薄板材的余高形状可以完全按照等厚板低匹配对接接头的弯曲等承载设计，即按照临界曲线hmin（x）公式（1）进行设计且焊趾部位圆滑过渡。对于焊缝竖直中心线右侧靠近厚板材的余高形状设计以降低应力集中且圆滑过渡为原则。由于理论最低余高临界曲线hmin（x）与板厚坡口处相交，为了避免相交处的截面突变产生较大应力集中，在焊缝中心最低余高点[0，hmin（0）]与厚板侧的坡口与母材表面交点 [Xw1，hmin（Xw1）]之间进行圆滑过渡，并与左侧理论最低余高临界曲线hmin（x）相切形成圆弧，降低应力集中程度，此圆弧半径为r2。不等厚板对接接头总熔宽也发生了变化，即w+Xw1=wmin+wr+Xw1。图5为不等厚板低匹配对接接头余高形状设计示意图。

为了工程上應用的方便，文献[11]已经给出圆弧可以覆盖并替代抛物线临界曲线，因此靠近薄板材侧的余高临界曲线hmin（x）可以利用圆弧Rmin替代，焊趾处圆弧过渡（半径为r1），靠近厚板材侧的余高形状设计成过渡圆弧（半径为r2），而且圆弧Rmin同时与焊趾处圆弧r1和过渡圆弧r2分别相切，将不等厚板低匹配对接接头设计成新的三圆相切形状，其示意图，如图6所示。

3 不等厚板低匹配接头有限元验证

采用MARC有限元模拟软件对不等厚板低匹配对接接头进行了有限元验证，并与标准推荐的不等厚板凹形与凸形圆弧过渡等匹配对接接头进行了比较。按照国家标准GB/T 2653—2008《焊接接头弯曲试验方法》建立有限元模型，薄板厚度2t1=10 mm，厚板厚度2t2=18 mm，长度为200 mm，宽度20 mm，V形坡口，坡口角度为α=60°，钝边高度为b=2 mm，钝边间隙为a=2 mm。压头半径为5 mm，厚板侧支辊半径为30 mm，薄板侧支辊半径为38 mm，跨距为110 mm。建模时，母材与焊缝金属力学性能见表1。

图7为不等厚板凹形圆弧过渡等匹配对接接头有限元模拟结果。图8为不等厚板凸形圆弧过渡等匹配对接接头有限元模拟结果。 由图7和图8可以看出，在弹性极限状态下，即等匹配接头焊缝金属屈服强度达到本身的屈服强度685 MPa时，不等厚板凸形圆弧过渡等匹配对接接头最大弯曲载荷为5 600 N，不等厚板凹形圆弧过渡等匹配对接接头最大弯曲载荷为3 400 N;凹形圆弧过渡的等匹配对接接头反而先于凸形圆弧过渡的等匹配对接接头达到屈服强度，发生屈服的位置均位于加载的焊缝底部中心。说明等匹配对接接头采用凸形圆弧过渡反而比凹形圆弧过渡承载能力高。

不等厚板低匹配对接接头有限元建模几何参量为：焊缝中心最低余高高度hmin（0）=2.8 mm，薄板侧最小半熔宽wmin=21.3 mm，总熔宽w+Xw1=33.1 mm，焊趾圆弧半径r1=20 mm，厚板侧圆弧过渡半径r2=13 mm。图9为不等厚板低匹配对接接头有限元模拟结果。不等厚板三圆相切低匹配对接接头余高圆弧半径Rmin=84 mm，盖面焊总熔宽w+Xw1=36.2 mm，其它几何参量与不等厚板低匹配对接接头相同。图10为不等厚板三圆相切低匹配对接接头有限元模拟结果。

由圖7和图8可以看出，在弹性极限状态下，即低匹配接头焊缝金属屈服强度达到本身的屈服强度420 MPa时，按照理论设计的不等厚板低匹配对接接头最大弯曲载荷为4 600 N，不等厚板三圆相切低匹配对接接头最大弯曲载荷为4 800 N，发生屈服的位置也均位于加载的焊缝底部中心。说明按照理论设计的不等厚板低匹配对接接头与不等厚板三圆相切低匹配对接接头的弯曲承载能力相当，均优于不等厚板凹形圆弧过渡等匹配对接接头，但是均略低于不等厚板凸形圆弧过渡等匹配对接接头，分别达到了凸形圆弧过渡等匹配对接接头的82.1%与85.7%。

分析其承载能力高低原因：在接头屈服强度匹配比一定情况下，接头弯曲承载能力取决于距离加载中心远近与各个横截面的承载面积，因此在接头宽度和加载距离固定的条件下，接头弯曲承载能力取决于横截面的高度。在该研究中，凸形圆弧过渡等匹配对接接头焊缝中心处的余高高度（5.7 mm）远高于不等厚板低匹配对接接头（2.8 mm）与凹形圆弧过渡等匹配对接接头（0.82 mm），是导致凸形圆弧过渡等匹配对接接头弯曲承载能力高的主要原因。在弯曲载荷作用下，凸形圆弧过渡具有明显的优势。

4 结论

（1）对不等厚板低匹配对接接头按照弯曲等承载能力对余高、熔宽等几何参量进行重新设计，对于靠近薄板材侧的余高形状可以按照等厚板低匹配对接接头弯曲等承载设计方法进行设计，对于靠近厚板材侧的余高形状以圆滑过渡形式进行设计。

（2）为了工程上应用的方便，根据圆弧覆盖并替代抛物线的可行性，靠近厚板材一侧的余高临界曲线利用圆弧替代，圆弧分别与焊趾处圆弧和厚板材侧的过渡圆弧相切，将不等厚板低匹配对接接头设计成新的三圆相切形状。

（3）有限元验证模拟结果表明，按照理论设计的不等厚板低匹配对接接头的弯曲承载能力与不等厚板三圆相切低匹配对接接头相当，均优于不等厚板凹形圆弧过渡等匹配对接接头，但是均略低于不等厚板凸形圆弧过渡等匹配对接接头。

参考文献

[1] 李亚江， 王娟， 刘鹏.低合金钢焊接及其工程应用[M].北京：化学工业出版社， 2003.

[2] Mohtadi-Bonab M A， Szpunar J A， Razavi-Tousi S S. A comparative study of hydrogen induced cracking behavior in API 5L X60 and X70 pipeline steels[J]. Engineering Failure Analysis， 2013，33：163-175.

[3] Hao S， Schwalbe K H， Cornec A. The effect of yield strength mis-match on the fracture analysis of welded joints：slip-line field solutions for pure bending[J]. International Journal of Solids and Structures， 2000， 37（39）：5385-5411.

[4] 陈俐， 胡席远， 胡伦骥. 高强钢的激光焊接性研究[J]. 应用激光， 2003， 22（1）; 19-21.

[5] 郑梗梗， 徐学利， 王洪铎. 高强度管线钢焊接性影响因素分析[J]. 焊管， 2017， 39（1）：36-40.

[6] Wang T， Yang J G， Liu X S， et al. Solution of stress intensity factor for mode I centre crack in undermatched butt joint with certain reinforcement[J]. Science & Technology of Welding & Joining， 2012， 17（3）：191-195.

[7] 王佳杰， 董志波， 刘雪松， 等. 弹性阶段低匹配对接接头三点弯曲余高形状设计[J]. 焊接学报， 2012， 33（8）：37-40.

[8] 赵智力， 方洪渊， 杨建国， 等.一种针对低匹配焊接接头的“等承载”设计方法[J]. 焊接学报， 2011， 32（4）：87-90.

[9] 赵智力， 张远健， 方洪渊， 等.低匹配十字接头的“等承载”设计[J]. 焊接学报， 2015， 36（6）：99-102.

[10] 郭军礼， 董志波， 刘雪松， 等. 基于等承载思想的低匹配T型接头设计[J].机械工程学报， 2019， 55（6）：1-10.

[11] 王佳杰， 方洪渊， 张敬强， 等. 弹性状态低匹配焊接接头弯曲等承载设计准则与设计方法[J]. 焊接学报， 2016， 37（7）：53-56.

[12] 方洪渊. 焊接结构的等承载设计[J]. 黑龙江科学， 2018， 37（7）：27-30.