中考中的概率题

关旸

应用等可能條件下的概率知识解决问题，是各地中考的重点内容之一。考题以选择题、填空题、解答题为主。在各地中考试卷的解答题中，分值在6至10分不等。

下面我们以中考真题的解答题中关于“等可能条件下的概率”内容进行整理和分析，希望对各位同学今后的学习有所启迪。

一、列表型

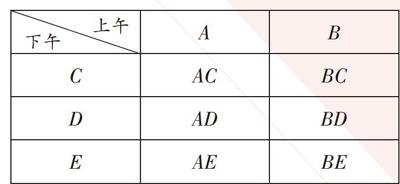
例1 （2018·泰州）泰州具有丰富的旅游资源，小明利用周日来泰州游玩，上午从A、B两个景点中任意选择一个游玩，下午从C、D、E三个景点中任意选择一个游玩。用列表或画树状图的方法列出所有等可能的结果，并求小明恰好选中景点B和C的概率。

【分析】此题主要考查了列表法和画树状图法求概率，列表法可以不重复不遗漏地列出所有可能的结果，适合于两步完成的事件。解题时还要注意是放回试验还是不放回试验。

通过列表展示所有6种等可能的结果数，找出小明恰好选中B和C这两处景点的结果数，然后根据概率公式求解。

解：列表表示结果如下：

[ A B C AC BC D AD BD E AE BE ][上午][下午]

由表可知共有6种等可能的结果数，其中小明恰好选中景点B和C的结果有1种，所以小明恰好选中景点B和C的概率为[16]。

二、写编号型

例2 （2018·徐州）不透明的袋中装有1个红球与2个白球，这些球除颜色外都相同，将其搅匀。

（1）从中摸出1个球，恰为红球的概率等于;

（2）从中同时摸出2个球，摸到红球的概率是多少？（用画树状图或列表的方法写出分析过程）

【分析】本题考查了列表法与画树状图法、概率公式等知识点。解题时还要注意是放回试验还是不放回试验。因为“同时摸出2个球”，因此是一个不放回的试验。

解：（1）将两个白球编号为白1、白2。从红球、白1、白2这三个球中任意摸出1个球，恰为红球的概率等于[13];

（2）画树状图表示结果：

共有6种等可能的结果，其中含红球的有4种结果，所以同时摸出2个球，摸到红球的概率P=[46]=[23]。

答：从中同时摸出2个球，摸到红球的概率是[23]。

三、不放回型

例3 （2018·扬州）4张相同的卡片上分别写有数字-1、-3、4、6，将卡片的背面朝上，并洗匀。

（1）从中任意抽取1张，抽到的数字是奇数的概率是;

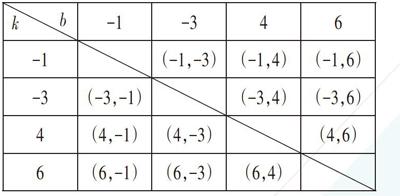
（2）从中任意抽取1张，并将所取卡片上的数字记作一次函数y=kx+b中的k;再从余下的卡片中任意抽取1张，并将所取卡片上的数字记作一次函数y=kx+b中的b。利用画树状图或列表的方法，求这个一次函数的图像经过第一、二、四象限的概率。

【分析】本题考查了列表法与画树状图法：利用列表法或画树状图法展示所有等可能的结果n，再从中选出符合事件的结果数目m，然后利用概率公式计算事件的概率。此外，本题也考查了一次函数的性质。

（1）直接利用概率公式求解;

（2）解题时还要注意是放回试验还是不放回试验;因为从余下的卡片中再抽一张，因此这是一个不放回的试验。

列表法展示所有12种等可能的结果数，利用一次函数的性质，找出k<0，b>0的结果数，然后根据概率公式求解。

解：（1）从中任意抽取1张，牌上写有数字-1、-3、4、6这四种等可能的结果，其中奇数有两种，所以概率是[24]=[12]。

（2）列表表示结果如下：

[k b -1 -3 4 6 -1 （-1，-3） （-1，4） （-1，6） -3 （-3，-1） （-3，4） （-3，6） 4 （4，-1） （4，-3） （4，6） 6 （6，-1） （6，-3） （6，4） ]

根据题意得：一次函数图像过第一、二、四象限，则k<0，b>0。

由表格可知总共有12种等可能的结果，其中经过第一、二、四象限的有4种，

∴图像经过第一、二、四象限的概率是[412]=[13]。

（作者单位：江苏省常州市第四中学）