一个基于无约束优化方法的交通组合模型

胡文君，周溪召

(1.上海中侨职业技术学院 经济与管理学院，上海 201309； 2. 上海理工大学 管理学院，上海 200093)

0 引 言

由交通生成、交通分布、模式划分和交通分配4个阶段构成的“四阶段预测”模型是交通规划和预测中常用的模型方法，但这种方法割裂了各阶段之间的相互联系。为克服这一不足，许多研究人员将4个阶段中的两个或多个阶段结合，建立一个组合模型，如交通生成与分布组合模型[1]、交通分布与交通分配组合模型[2-3]、方式划分与分配组合模型[4]或交通生成、分布、方式划分、分配组合模型[5-6]。

在由两个或更多阶段构成的组合模型中，数学规划法[7-8]、非线性互补[9]、变分不等式[10]、基于出行链的方法[11]及构建超级网络方法[12]是学界中常用的方法，很少有研究者采用无约束优化方法。

无约束优化方法在通讯、计算机、控制、工程和管理等领域有着广泛应用[13-14]，它是非线性规划中的一种，是许多带约束优化问题研究的基础。该方法没有等式或不等式约束，其思想是寻求多元函数y=f(x1,x2,Λ,xn)在整个实n维空间Rn中的局部最小值。在实际应用中，许多情景被抽象为函数形式后均为凸函数。对于凸函数，局部最小值点即为全局最小值点，因此只要能求得这类函数的一个局部最小值点，该点一定为全局最小值点。

采用无约束优化方法，笔者建立了一个组合出行-终点-模式-路径选择模型，提出了组合模型的无约束最小化一般公式，分析了解的性质，推导了该无约束最小化一般模型与组合模型解的等价性，解的存在性和唯一性。将之推广到基于多项式Logit(multinomial logit, MNL)和C-Logit的无约束优化组合模型。最后用一个简单算例证明了模型可行性和有效性。

1 符号和假设

1.1 符号定义

r为一个起点；s为一个终点；j为一种模式；k为一条路径；R为起点集合；S为终点集合；J为模式集合；K为路径集合；Nr为从起点r出发的潜在出行需求量；Tr为起点r用户中选择出行的出行者流量；Trs为从起点r出发选择终点s的出行者流量；Trsj为从起点r出发到终点s，使用模式j的出行者流量；Trsjk为从起点r出发到终点s，使用模式j取道路径k的出行者流量；β为组合模型参数，βr,βs,βj,βk分别是与出行、终点、模式、路径相关的正参数；Pr为给定潜在出行需求条件下，出行者选择出行的概率；Ps∣r为给定起点r条件下，出行者选择终点s的概率；Pj∣rs为在起点r到终点s已经确定条件下，出行者选择模式j的概率；Pk∣rsj为在起点r到终点s模式j已经确定条件下，出行者选择路径k的概率；Wr为出行者在起点r所期望获得效用；Ws∣r为出行者从起点r到终点s所期望获得效用；Wj∣rs为出行者从起点r到终点s使用模式j所期望获得效用；Wk∣rsj为出行者从起点r到终点s使用模式j且取道路径k所期望获得效用；ga(xa)为出行者在路段a上的出行阻抗函数；gr(Tr)为出行者从起点r出发的出行阻抗函数；grs(Trs)为出行者从起点r出发驶向终点s的出行阻抗函数；grsj(Trsj)为出行者从起点r出发驶向终点s采用模式j的出行阻抗函数；grsjk(Trsjk)为出行者从起点r出发驶向终点s采用模式j取道路径k的出行阻抗函数。

1.2 模型假设

假定某个出行者对出行、终点、模式和路径的选择符合一个自上而下的层级结构，在每一层次做出选择取决于上一层次的选择。首先在第1层，一个潜在出行者Nr决定是否出行，形成两种可能：出行和不出行，Tr为出行流，Pr是一个潜在出行者决定出行概率；第2层决定出行终点，若第1层选择出行，那么他/她在第2层选择一个终点s，形成条件概率Ps∣r；第3层决定出行模式，在第2层终点选择下，需要选择一种模式j，形成条件概率Pj∣rs；第4层决定出行路径，需要选择从r到s模式j下的一条路径k，形成条件概率Pk∣rsj。

组合模型中假定层级结构如图1，与文献[15]给出的结构类似。

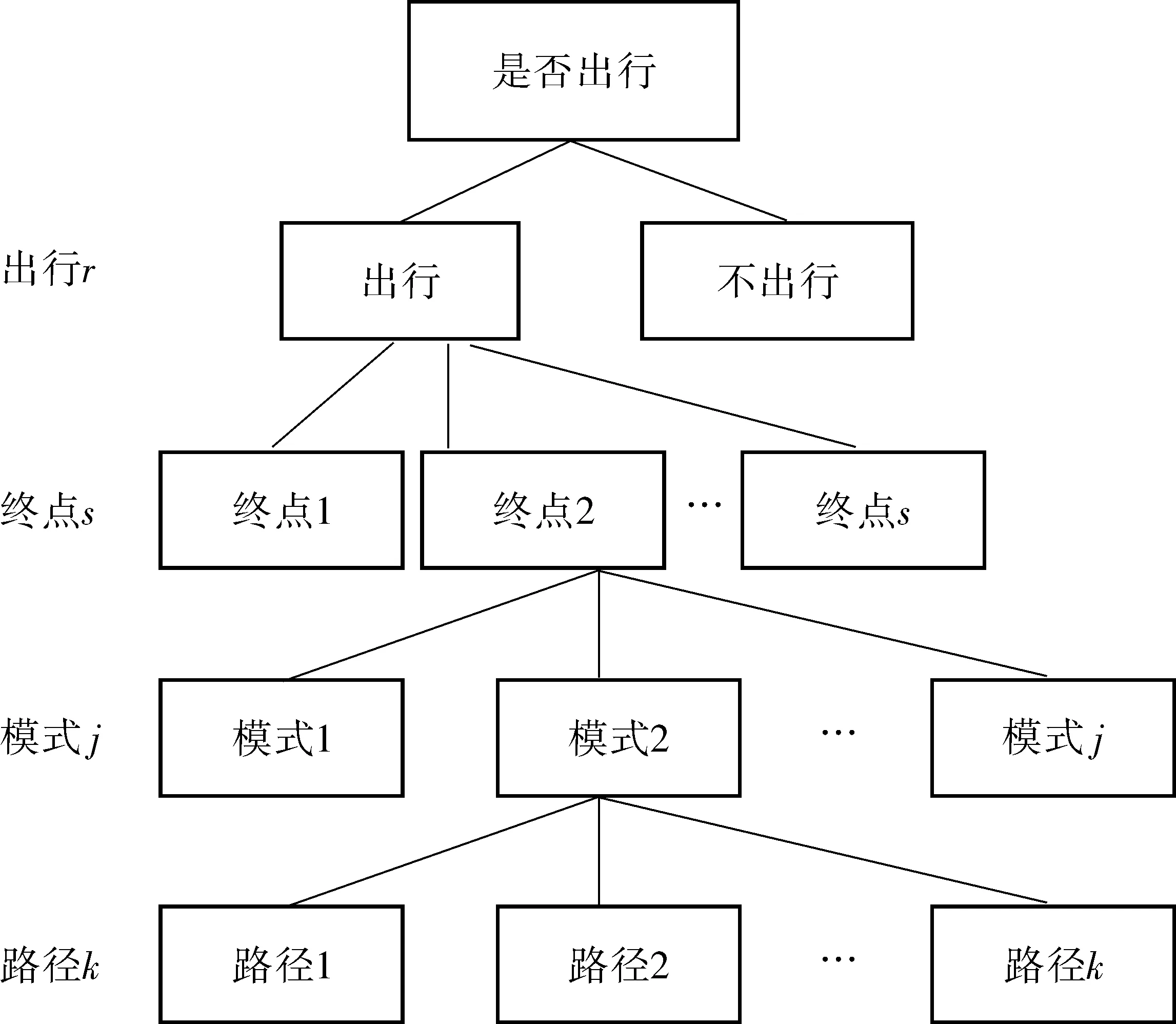
图1 组合出行、终点、模式、路径选择层次结构Fig. 1 Hierarchical structure of combined travel, destination, mode and route choice

假定Nr为起点r的潜在出行需求，Tr为起点r出行者中选择出行的出行者流量，Pr为给定潜在出行需求的条件下，出行者选择出行概率，如式(1)：

Tr=Nr·Pr

(1)

类似地，当从起点r出发，驶往终点s的出行者流量满足式(2)：

Trs=Tr·Ps|r

(2)

同理，从起点r出发到终点s的出行者，选择模式j的流量如式(3)：

Trsj=Trs·Pj|rs

(3)

从起点r出发到终点s的出行者，使用模式j的出行者选择路径k的流量可通过从路径选择阶段到出行选择阶段层次结构中每一阶段条件概率相乘得到，如式(4)：

Trsjk=Trsj·Pk|rsj=Nr·Pr·Ps|r·Pj|rs·Pk|rsj

(4)

根据期望效用理论，选择方案i的效用为：Ui=ui+εi。其中：ui为效用的确定性部分，反映了方案的属性和出行者的特征，εi为随机误差项，反映了效用中的不确定因素。

从起点r到终点s，使用模式j取道路径k的一次出行总效用可假设如式(5)：

Ursjk=ur+urs+ursj+ursjk+εr+εrs+εrsj+εrsjk

(5)

式中：ur,urs,ursj,ursjk分别是与出行、终点、模式和路径选择相关的系统效用；εr,εrs,εrsj,εrsjk分别是与4个阶段选择相关的误差项。

假定有式(6)：

(6)

式中：grs(·)是从起点r到终点s的广义出行阻抗(负效用函数)；gr(·)是出行的负效用函数；grsj(·)是从起点r到终点s使用模式j的负效用函数；grsjk(·)是从起点r到终点s使用模式j取道路径k的负效用函数。

给定已选择的起点r、终点s和模式j，一个出行者在一次出行中选择路径k的条件概率的效用等于：Wk∣rsj=ursjr+εrsjk；给定已选择的起点r和终点s，出行者在一次出行中选择模式j的条件概率效用如式(7)、(8)：

Uj|rs=uj|rs+εrsj=ursj+Wj|rs+εrsj

(7)

Wj|rs=E(maxUk|rsj)

(8)

式中：Wg∣rs表示从起点r到终点s使用模式j的期望获得效用(满意函数)。

从起点r到终点s的期望获得效用和在起点r的期望获得效用分别如式(9)、(10)：

Ws|r=E(maxUj|rs)

(9)

Wr=E(maxUr|s)

(10)

根据满意函数W特征，满意函数对一个方案的系统效用偏导数等于该方案选择概率，即为∂W(U)/∂Ui=Pi(U)，可知出行者在每一层选择路径、模式、终点的概率分别如式(11)～(13)：

(11)

(12)

(13)

2 组合无约束优化模型

2.1 组合无约束优化基本模型

在组合模型中，当用户未能通过单方面改变其出行、终点、模式和路径选择来改善其获得的效用时，可达到模型均衡状态。当达到均衡状态时，存在一个可行流模式T=[Tr,Trs,Trsj,Trsjk]，满足式(1)～(4)。

若路径出行阻抗可加，则可将路段流表示为经过该路段所有路径的路径流之和，如式(14)：

(14)

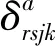
同时，对终点、模式和路径需满足以下网络流守恒约束，如式(15)～(17)：

(15)

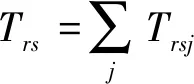
(16)

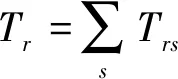
(17)

在一个N为节点集，A为路段集的交通网络G(N,A)中，假如网络中出行者的阻抗函数ga(xa),gr(Tr),grs(Trs),grsj(Trsj),grsjk(Trsjk)是连续、可微、严格增且可分的，只取决于该路段、出行、终点、模式或路径自身的流，且广义阻抗函数grsjk(·)可加，则可将组合模型表现为一个无约束最小化问题Z1，如式(18)：

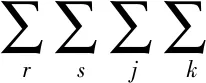
(18)

式中：ga(xa)表示路段a上的广义阻抗函数；gr(Tr),grs(Trs),grsj(Trsj),grsjk(Trsjk)分别表示与出行、终点、模式和路径相关的广义阻抗函数，当gr(Tr),grs(Trs),grsj(Trsj),grsjk(Trsjk)为常数时，相关变量可去除，这表明目标函数不会受这几个参数影响。

2.2 模型解的特征分析

2.2.1 解的等价性

解的等价性是证明无约束优化模型〔式(18)〕恰为组合模型的路段流、出行流、终点流、模式流和路径流解。

首先求解目标函数Z1对路段a上流量xa的偏导数。当路段阻抗函数ga(xa)连续、可微且可分时，路径阻抗函数grsjk可表示为经过该路径所有路段之和的函数相加，如式(19)：

(19)

目标函数中第1项对路段流的偏导数如式(20)：

(20)

目标函数中第2、3项对路段流xa偏导数如式(21)：

(21)

目标函数中第4、 5项和第5、 6项对路段流xa的偏导数如式(22)：

(22)

目标函数中第8、 9项和第10、 11项对路段流xa的偏导数如式(23)：

(23)

综合式(20)～(23)，可得式(24)：

(24)

由于路段阻抗函数严格增，∂ga(xa)/∂xa≠0，则有式(25)：

(25)

式 (25)为式(14)给出的均衡路段流。

目标函数式(18)对出行流Tr求偏导。目标函数式(21)的第1项对Tr偏导如式(26)：

(26)

同理，目标函数的第4、5项对Tr的偏导如式(27)：

(27)

其余几项对Tr的偏导均为0。由于gr(Tr)严格增，即∂gr(Tr)/∂Tr≠0，可式(28)：

Tr=Nr·Pr

(28)

式(28)恰为式(1)给出的均衡出行流。

目标函数式(18)对终点流Trs求偏导，如式(29)：

(29)

由于grs(Trs)严格增，即∂grs(Trs)/∂Trs≠0，得式(30)：

Trs=Tr·Ps|r

(30)

式(30)恰为式(2)给出的均衡终点流。

同理，目标函数式(18)对Trsj和Trsjk的偏导如式(31)、(32)：

Trsj=Tr·Ps|r·Pj|rs=Trs·Pj|rs

(31)

Trsjk=Tr·Ps|r·Pj|rs·Pk|rsj=Trsj·Pk|rsj

(32)

式 (31)恰为式(3)给出的均衡模式流；式(32)恰为式(4)给出的均衡路径流。

综上，无约束最小化问题最优解给出了均衡的出行流、终点流、模式流和路径流。因此，提出无约束最小化模型等价于组合出行-终点-模式-路径选择模型。

2.2.2 解的存在性和唯一性

目标函数式(18)对路径流Trsjk的偏导数如式(33)：

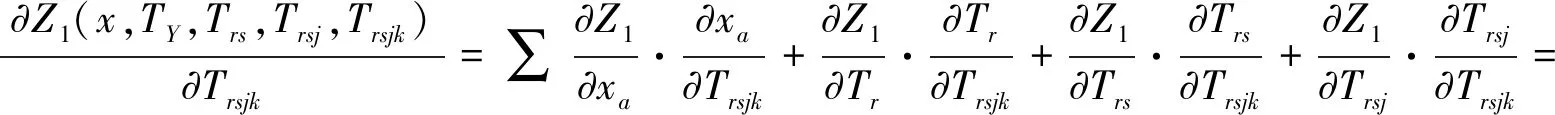
(33)

式(33)中各项均为严格凸函数，则目标`函数Z1为严格凸函数，且当∂Z1/∂Trsjk=0时，得到Trsjk=Tr·Ps∣r·Pj∣rs·Pk∣rsj为模型的解，因此所构造模型有解且有唯一解。

2.3 模型拓展

2.3.1 基于MNL的组合无约束最小化模型

多项式Logit(MNL)结构可视为提出的无约束最小化模型的特例。在MNL中，每阶段出行者的选择概率服从一个层级MNL结构，如式(34)～(37)：

(34)

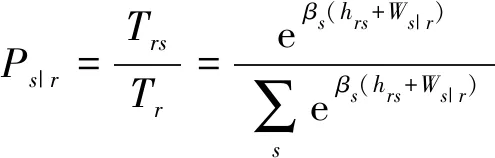
(35)

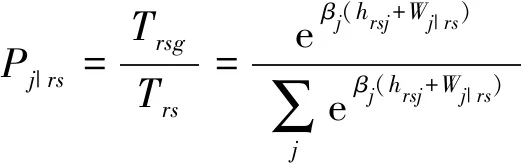
(36)

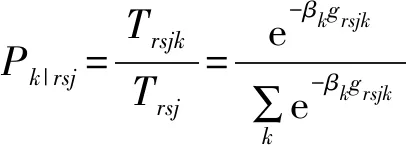
(37)

式中：Wr、Ws∣r、Wms∣r、Wj∣rs、Wk∣rsj分别为出行、终点、模式、路径选择阶段的期望获得效用。

在MNL路径选择下分别如式(38)～(41)：

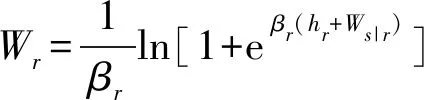
(38)

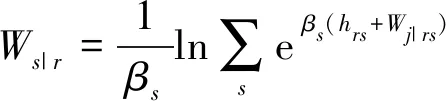
(39)

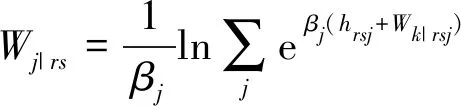
(40)

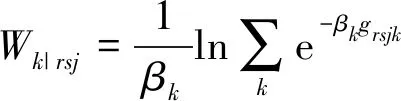
(41)

MNL结构下的组合无约束最小化问题如式(42)：

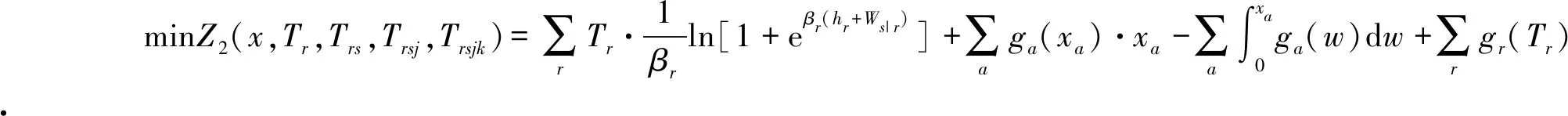
(42)

Ws|r满足式(39)，进而满足式(40)、(41)。式(42)可作为式(18)的一个特例，且与式(18)类似，如式(43)～(46)：

(43)

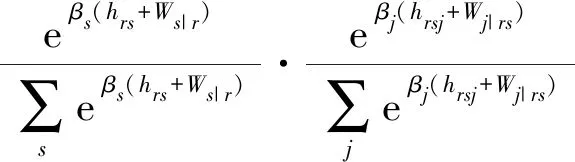
(44)

(45)

(46)

式(42)～(46)给出无约束最小化问题的最优解满足均衡条件且能求解得到MNL下组合模型的唯一均衡出行流、终点流、模式流与路径流解。

2.3.2 基于C-Logit的组合无约束最小化模型

在路径选择行为中，为反映更常见的路径重叠问题，笔者采用C-Logit模型[16]来处理路径重叠问题。C-Logit模型由其解析闭型概率表达式、较少的校正、符合随机效用理论的较理性行为而受到广泛应用。其采用一个系统效用项中的共同因子(CF)来解释重叠路径。

在C-Logit模型中，选择一条路径k的概率如式(47)：

(47)

式中：θ为与路径选择相关的参数；CF为路径重叠参数。

一个典型的CF形式如式(48)：

r∈R,s∈S

(48)

式中：Lkl为路径k和l共同路径的长度；Lk和Ll分别为路径k和l的长度；η1、η2分别为参数，若η1=0，则CF因子为0，C-Logit模型退化为传统的MNL模型。

在组合模型路径选择层，采用C-Logit模型表示，如式(49)：

(49)

其中：CF因子满足式(48)的形式。其他层次选择概率与MNL相同，服从式(34)～(36)。则C-Logit模型下的无约束最小化问题与式(42)的形式相同。其中：Ws∣r满足式(39)，进而满足式(40)、(50)。式(50)表述为：

(50)

与MNL下的无约束优化公式类似，可得式(51)～(54)：

(51)

(52)

(53)

(54)

式(50)～(54)给出无约束最小化问题的最优解满足均衡条件且能求解得到C-Logit下组合模型的唯一均衡出行流、终点流、模式流与路径流解。

3 算法和算例

在求解无约束优化问题时，最速下降法是一常用的求解算法。它选取一个目标函数值下降最快的方法，以利于尽快地达到极小点。这种算法关键是最速下降法的选取，一般取负梯度作为最速下降方向，然后进行一维搜索，当满足精度要求时则停止计算。其一般步骤为：

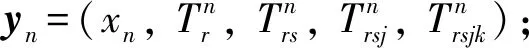
4)步骤四：移动。yn+1=yn-yn·ynZ(yn)；

最速下降法中，最主要的步骤是下降方向确定和线性搜索。条件概率Pr、Ps|r、Pj|rs、Pk|rsj分别由式(34)～(37)(MNL无约束模型中)或式(47)～(49)(C-Logit无约束模型中)给出。

用一个简单算例来研究提出的模型特征。使用一个如图2的网络，包含3个OD对1-3、1-4、1-5，5个节点和8个路段。OD对和路段、路径间的对应关系见表1。

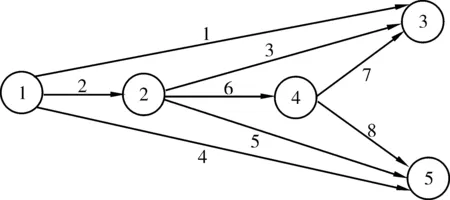
图2 一个简单网络Fig. 2 A simple network

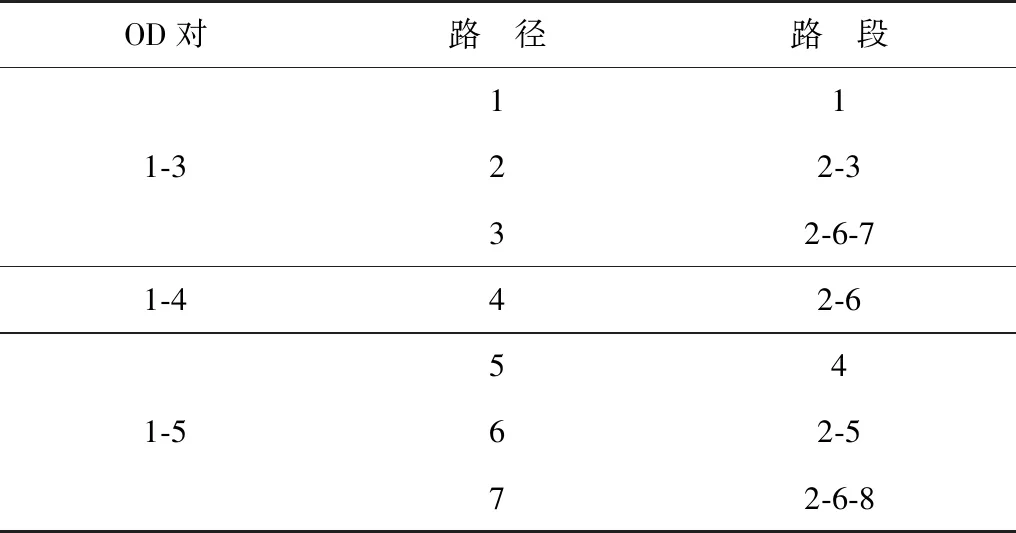
表1 OD对和路段、路径间的对应关系Table 1 Correspondence among OD pair, road section and paths

假定网络中仅有两种模式：汽车和公交，为方便分析用1和2表示，即j=1表示汽车，j=2表示公交。两种模式网络有相同的拓扑结构且相互独立。

假设汽车网络的路段、终点、OD对和路径的负效用函数分别用式(55)表示：

(55)

则汽车网络的路段、终点、OD对和路径负效用函数分别如式(56)：

(56)

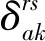
设与出行选择、终点、模式相关参数βr,βs,βj=1，与路径选择相关的参数βk=0.5。从起点1出发的潜在出行者数N1=1 000，吸引力h1=5。OD对1-4和1-5吸引力分别为h14=3.5，h15=3.8；OD对1-4间汽车和公交两种模式吸引力分别为h141=3.5，h142=3.6；OD对1-5间汽车和公交两种模式的吸引力为h151=3.8，h152=3.4。OD对间每一路段自由流出行时间均为500，如表2。

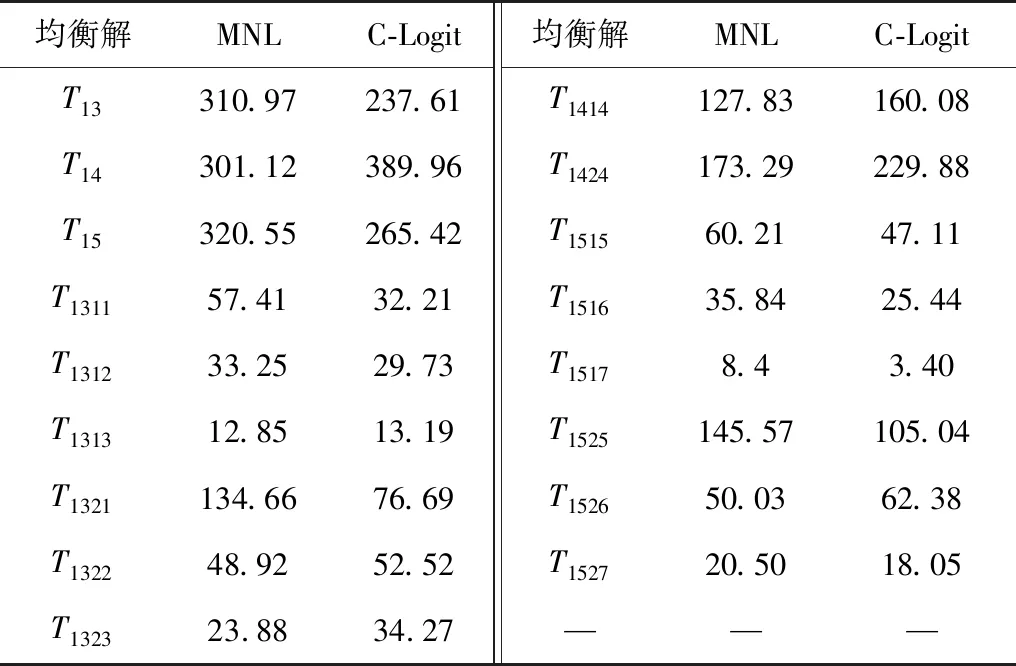
表2 终点和路径选择阶段均衡流量结果Table 2 Equilibrium flow results in terminal and route selection stages

为反映路径重叠效应对均衡解的影响，采用基于C-Logit的无约束优化模型进行再求解。仍采用上述参数和负效用函数形式。另外，令式(48)中CF参数η1=0.9，η2=0.8。各路段长度为：路段2、6、7、8长度为5；路段1、4长度为12；路段3、5长度为8。可知路径2、3重叠部分，以及路径6、7的重叠部分即为路段2的长度。计算得到终点选择阶段和路径选择阶段均衡解如表2第3列。

由表2知在C-Logit组合模型中，路段流会随路径重叠而变化，其对路径流量进行分配时，相对MNL下的组合模型，重叠路径上被分配到的流量会减少，而非重叠路径上被分配到的流量会相应增加，以保持流量守恒，这说明传统MNL会高估重叠路径流，而低估非重叠路径流。同理，OD流也会随路径重叠而变化，通过改变每一OD对的吸引力来改变OD流变化，有重叠路径OD对会使自身吸引力下降，因而使OD需求减少，反之没有重叠路径的OD对会使自身吸引力上升，OD需求增加。即OD对(1, 3)和(1, 5)间需求减少，OD对(1, 4)间需求增加，这说明MNL会高估重叠路径OD需求水平，而低估非重叠路径OD需求水平。

4 结 论

为克服传统的4步骤序列模型不同阶段中行为不一致问题，笔者采用了一个组合出行-终点-模式-路径选择模型，将出行与否的选择、出行终点选择、模式选择和交通分配纳入一个统一的框架进行分析；分析了组合模型在期望效用理论下的出行阻抗、用户分别选择出行、终点、模式和路径的概率或条件概率，及满意函数和特征；建立了组合模型的一般无约束优化公式；分析了解的性质，证明了一般无约束优化公式与带约束组合模型解的等价性、存在性和唯一性；并将模型推广到服从多项式Logit和C-Logit组合模型无约束优化公式；用算法和算例证明了模型的可行性和有效性。

结果表明：无约束优化公式与带约束的组合模型公式在求解均衡解方面是等价的。且路径重叠效应会对均衡路径流分配产生影响，同时通过影响OD对的吸引力来对有重叠路径的OD对的需求水平产生影响。