表格图像转换成Word表格的研究

姚鹏威，杨 炯，张爱梅，黄 晓

(郑州大学 机械工程学院， 河南 郑州 450001)

随着计算机技术的高速发展，人类社会各方面信息的更新与传递也更加快捷和便利。然而，传统纸质表格存储的信息不易管理与交换，已经无法满足人们的需求。市场上的识别软件以识别纯文字的居多，这些产品能完成简单表格图像的转换，但无法很好地完成简历类、采购单类和信息采集类表格的转换。有些产品需要自己的模板库，对于复杂多变的简历类表格有时无法完成匹配，也就无法完成表格图像中表格的提取。还有一些产品对图像的要求较高，如图像大小、位深度和分辨率。基于以上情况，本文将纸质表格扫描成图像并保存为图片，利用图像处理技术在Word中绘制可编辑的电子表格，从而大大提高信息录入的效率，有利于实现从纸质表格到电子表格的转换。

1 提取图像横线和竖线的端点坐标

本文采用BRISK方法实现表格图像中特征点的检测和描述，通过筛选提取表格的4个角点和图像的4个角点，然后以图像的4个角点为模板利用透视变换完成表格图像的倾斜校正。接着对其进行图像预处理，提取表格图像的横线和竖线并对其进行修复和细化。本文采用投影法完成表格横线和竖线的细化，利用Shi-Tomasi角点检测完成表格图像中横线和竖线端点坐标的提取。算法流程如图1所示。

图1 横线和竖线端点提取算法流程

1.1 表格图像倾斜校正

首先，进行光照均衡化预处理，目的是消除光照变化的影响，增强对比度，这样有利于特征点的检测。利用BRISK方法完成特征点的检测，然后对特征点进行两次筛选以去除干扰点。第1次筛选时，文字上的特征点数量多且密集，因此可以采用密度聚类的思想去除文字上的特征点，方法是以每一个特征点为圆心、给定距离为半径建立累加器，当累加器的数量大于一定数量时，判断为杂点，然后将其去除。第2次筛选时，首先判断特征点是否存在重叠，若存在则对重叠的特征点进行特征响应值的判断，保留特征响应值较强的特征点，删除响应值小的特征点，从而达到去除杂点的目的。通过对倾斜表格分析可知：表格边框4个角点的坐标x和y值要么最大要么最小，根据这一特征得到表格边框的4个角点坐标，然后用表格边框的4个角点坐标与表格图像的4个角点坐标进行距离比较，从而完成表格边框4个角点和图像4个角点的一一对应。接下来利用透视变换实现表格图像的倾斜校正。

1.1.1利用BRISK方法检测特征点

BRISK方法[1]是BRIEF算法的改进，也是一种基于二进制编码的特征描述子，对噪声有很好的鲁棒性，并且具有尺度不变性和旋转不变性。它采用FAST算法进行特征点检测，为了满足尺度不变性，通过构造图像金字塔在多尺度空间内进行特征点检测。

在BRISK框架下，其尺度空间金字塔由n个组层(用ci表示)和n个组间层(用di表示)组成，其中i={0，1，2，…，n-1},组间层di在组层ci和ci+1之间，一般情况下n=4。c0层是原图像，c1层是c0的2倍下采样得到，c2层是在c1层的2倍下采样得到，ci层是在ci-1层的2倍下采样得到。组间层d0是由原始图像c0层的1.5倍下采样得到。d1层是d0的2倍下采样得到，d2层是在d1层的2倍下采样得到，di层是在di-1层的2倍下采样得到。图像尺度用t表示，则每个组层的尺度为[2-3]

t(ci)=2i

(1)

每个组间层的尺度为

t(di)=1.5×2i

(2)

尺度空间金字塔建立后，对每个组层和组间层采用FAST角点检测算法检测特征点。对检测到的特征点进行非极大值抑制,去掉鲁棒性差的特征点。比较它们的角点响应值即得分值，非特征点得分值为0。利用最小二乘法提取特征点的位置信息。本文以特征点检测常用的两种方法BRISK方法和SIFT方法[4]进行对比。由表1数据分析可知：BRISK方法检测的特征点多，速度快，从角度偏差看SIFT检测的特征点更准确，但是BRISK方法检测的特征点并不影响表格横线和竖线的提取，综合考虑采取BRISK方法完成特征点的检测。2种方法的对比分析见表1。

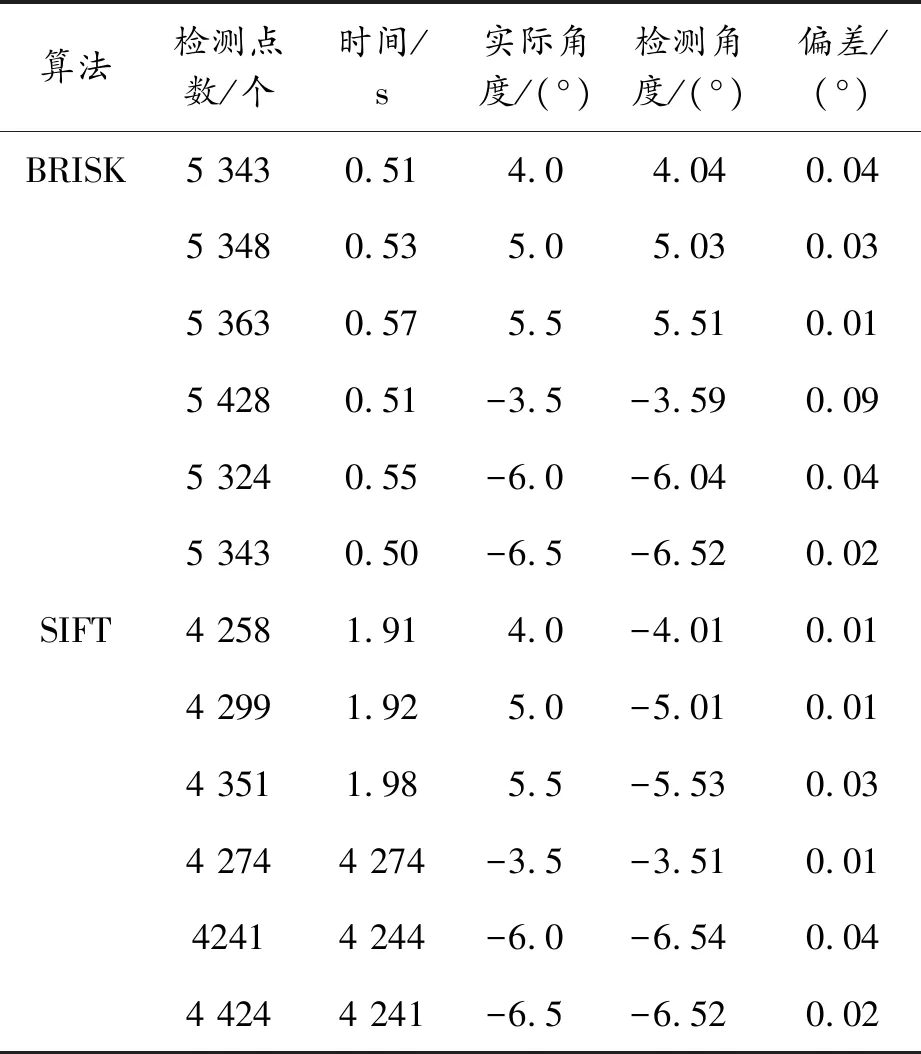
表1 BRISK方法和SIFT方法对比分析

1.1.2透视变换实现表格图像校正

确定了表格边框的4个角点和图像边框的4个角点后，以表格的4个角点为目标、图像的4个角点为模板获取变换矩阵，采用透视变换[5]达到校正表格图像的目的。

分别以表格的4个角点为原点计算每个角点到图像4个角点的距离，筛选出每组计算结果的最短距离，以此来确定表格4个角点的排列顺序。这时表格的4个角点和图像的4个角点就形成了一一对应的关系。

使用estimateAffine 2D方法生成变换矩为

(3)

特征矩阵R写成数学表达式为

R=T·s+b

(4)

其中：T旋转矩阵；s为缩放因子；b为平移矩阵。

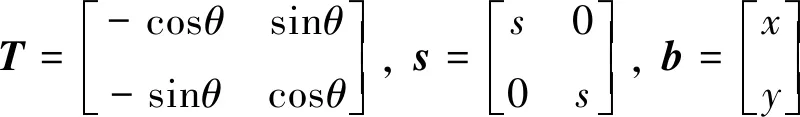
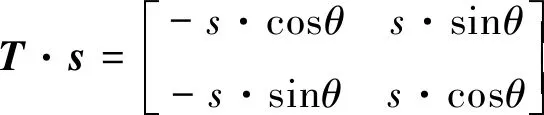
(5)

a2+b2=s2(cosθ2+sinθ2)=s2

(6)

因为透视变换使用的变换矩阵为3×3矩阵，因此需要对R矩阵进行补齐。补齐后的R矩阵为：

(7)

为了便于提取表格图像中表格横线和竖线端点坐标，保证表格图像矫正后大小保持不变。需要去除变换矩阵的缩放因子s，变换后的H矩阵为：

(8)

修改后的变换矩阵H使表格图像居中，使用矩阵H对表格的4个角点进行变换，变换后4个角点统一到图像的4个角点坐标所在的位置，使用逆变换求得移动变换矩阵H1。移动4个角点位置使表格图像居中,完成表格图像的倾斜校正。逆变换矩阵H1为：

(9)

表格图像倾斜校正前后如图2所示。

图2 校正前后的表格图像

1.2 表格图像预处理

图像预处理的目的是消除图像中冗杂的信息，增强有关信息的可检测性和最大限度地简化数据处理，从而有利于特征提取、图像分割和识别。

首先，对表格图像进行灰度化处理[6]。本文采用加权平均法对表格图像进行灰度化处理，其计算公式为[7]：

f(i,j)=0.11R(i,j)+0.59G(i,j)+

0.3B(i,j)

(10)

式中：R、G、B分别表示彩色图像中第i行第j列像素的红绿蓝3种颜色的亮度值；f(i,j)则是经转换得到的灰度图像中第i行第j列像素的灰度值。

然后，进行二值化处理[8]。二值化处理的阈值采用最大类间方差法计算，它可以自适应地进行阈值选择，即算法在实现过程中，让阈值遍历所有灰度级并计算其对应的类间方差。取使类间方差最大的灰度级作为二值化的阈值。

如果灰度阈值取值为T，则图像像素按灰度级被分为2类：前景C0和背景C1。则最佳阈值的求值公式为：

(11)

式中：μ为图像总平均灰度级；ω(T)表示C0类灰度级出现的概率；μ(T)表示C0类的平均灰度级。当方差σ2(T)最大时，前景和背景差异最大，灰度T为最佳阈值。

1.3 形态学处理方法提取表格横线和竖线

利用形态学处理方法[9]提取预处理后的表格图像的横线和竖线，通过采用最基本的两个形态学操作膨胀和腐蚀，用不同的结构元素实现对输入图像的处理以得到目标图像。

检测表格横线结构元素的Size宽度必须大于文字横线的最大宽度，目的是去除文字和竖线保留横线；检测表格竖线结构元素的Size高度必须大于文字竖线的最大高度，目的是去除文字和横线保留竖线。然后，用以上两种结构元素分别对图像的水平方向以及竖直方向做闭运算操作，以去除横线或竖线以外的细节干扰，得到表格横线和竖线并完成下一步表格横线和竖线的修复和细化。

1.3.1修复表格横线和竖线

图3所示为4种表格竖线的缺损情况，黑色部分为值是0的像素点，其他部分是像素值为255的待填充像素点，以剖面线部分为例进行填充。

如图3中(a)和(b)所示，遍历方式为从左向右，从上向下。图(a)待填充部分坐标为(i,j)，(i-1,j)像素值为0，在i行向后搜索像素值不为255的点，若有，则待填充部分为0，即填充为黑色像素点，其他缺失的像素点按照相同的方式进行填充。图(b)待填充坐标为(i,j)，(i,j-1)和(i-1,j)像素值为0，则待填充部分像素值应为0，即待填充部分为黑色像素，其他缺失的像素点按照相同的方式进行填充。

对于图3中(c)和(d)所示的情况，遍历方式为从右向左，从下向上。图(c)待填充部分坐标为(i,j)，(i-1,j)像素值为0，沿i行向前搜索像素值不为255的点，若有，则待填充部分为0，即填充为黑色像素点，其他缺失的像素点按照相同的方式进行填充。图(d)待填充坐标为(i,j)、(i,j-1)和(i-1,j)像素值为0，则待填充部分像素值应为0，即填充部分为黑色像素，其他缺失的像素点按照相同的方式进行填充。

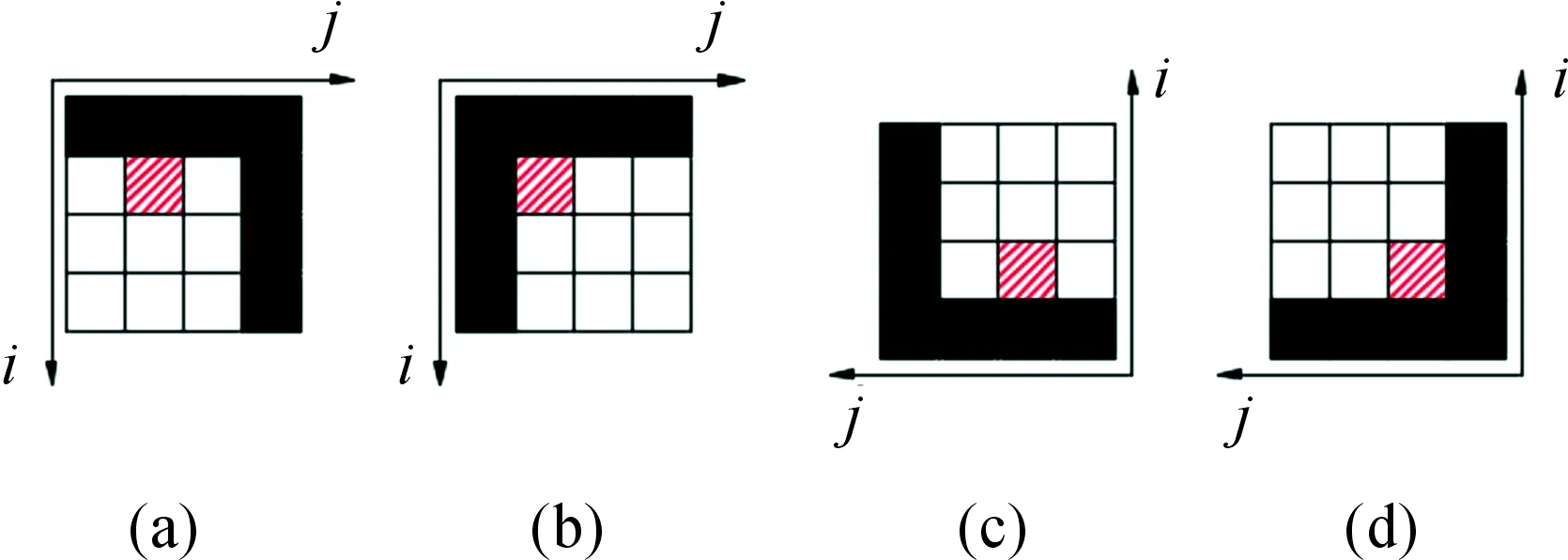
图3 直线修复示意图

同理，完成表格横线的4种缺损情况的修复。表格横线和竖线的修复前后对比如图4所示。

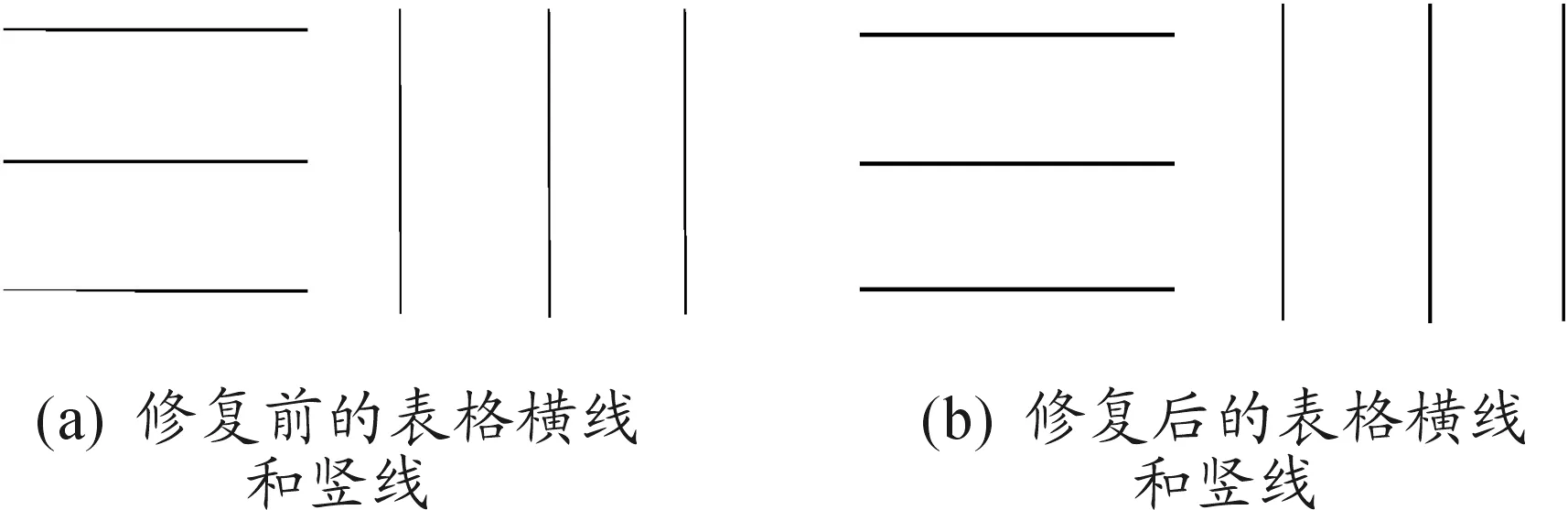
图4 表格横线和竖线修复前后对比

1.3.2利用投影法细化表格横线和竖线

在进行表格横线和竖线图像处理时，需要对图像进行细化，提取出图像的骨架信息，即原图像的中心线，有利于获取更加有效的端点坐标。利用投影法细化表格横线和竖线的算法流程如下：

步骤1对水平线进行从左向右投影。

步骤2从上向下遍历投影图最右端，获取每条水平线竖直方向的起点的和终点，也就是水平线的线宽。遍历图像，当像素值不为0时，记录该点位置为i，设定阈值k<15，建立累加器m。判定i+k行像素值是否为0。若不为0，累加器m+1，继续循环；若i+k点像素值为0时，结束循环，输出i和m，此时m为线宽。

步骤3若m为偶数，记录i+m/2行，此时i+m/2行为单像素行；若m为奇数，记录i+(m+1)/2行，此时i+(m+1)/2行为单像素行。

步骤4将所有单像素行从原图中提取出来并在所建与原图一样大小的空白图中保存,完成水平线细化。

竖直线细化同理，竖直线从下向上投影，遍历图像从左向右。

1.4 Shi-Tomas算法获取横线和竖线端点坐标

在本文1.3节表格横线和竖线提取中得到横线和竖线的灰度图后，分别对横线和竖线进行相应的形态学处理，寻找到相应的矩形轮廓，用每个相同位置的矩形轮廓框选细化后的表格横线和竖线，每次框选1条，并将其放到新建的大小相同的空白图像上。使用Shi-Tomasi角点检测方法[10]分别对新的图像进行角点检测并记录每条横线和竖线的端点坐标。

端点坐标的取值。由于倾斜校正和检测误差等因素会导致同一坐标的坐标值有偏差，不利于后面的表格绘制。因此，有必要对获得的端点坐标进行取值处理。行的形式为[xs,ys,xe,ye],先计算数据行与行之间x值坐标差值，如果差值小于3说明x值应相等，同取首个x值。然后比较行内部数据，如果|xs-xe|<3，说明xs=xe，同取首个x值。y的取值同理。

2 Word表格绘制

Word绘制表格的流程如下：

步骤1根据横线和竖线端点坐标统计得到m条横线和n条竖线。

步骤2Word生成(m-1)行和(n-1)列的表格。

步骤3合并单元格。

根据同一条横线端点坐标y值相同，即有m条横线，同一竖线端点坐标x值相同，有n条竖线，完成表格横线和竖线的统计。进而在Word中生成(m-1)行和(n-1)列的表格。

表格单元格的合并策略：对于横线，按照y值从小到大进行排序。对于竖线，则是x值从小到大进行排序。竖格合并，每个单元格标记为(i,j)(其中i=1,2,3…,j=1,2,3…)，单元格不进行合并的条件是ys=ye=y且xs≤x

图5 单元格合并类型

横格合并时，每个单元格标记为(i,j)，(其中i=1,2,3…,j=1,2,3…)，单元格不进行合并的条件是xs=xe=x且ys≤y

Word中自动生成的表格效果如图6。

图6 自动生成的表格效果

3 结束语

本文主要研究简历类、采购单类和信息采集类表格的扫描图像。通过对纸质表格的扫描图像进行倾斜校正，然后对表格图像预处理，实现了表格横线和竖线的提取、修复和细化，进而完成横线和竖线端点坐标的提取、数据处理和数据存储。利用提取的端点坐标在Word中完成表格的自动绘制，为表格图像内文字识别后填充到Word表格中准备条件，进而完成表格图像到可编辑电子表格的自动化转换。表格纸质化到电子化的转变为信息的存储和交换提供了极大的便利，具有广阔的应用前景。不足之处是识别表格种类较少和缺少文字填充，且图像获取方式存在局限性。下一步的研究重点是文字识别后的填充和票据类、快递单等复杂图像的识别以及数据的提取，还包括扩大图像的获取方式。