中性大气流动的CFD缩尺模拟方法

江升富，汪 新，赵冰春

（广东工业大学 土木与交通工程学院，广东 广州 510006）

在城市微气候研究领域，物理模型实验一般采用缩尺模型在风洞中进行，模型实验要求与原型之间满足一系列相似要求，但由于受限于风洞尺寸[1]以及采用的是真实介质，严格的相似要求难以满足[2].相对而言，CFD数值模拟技术由于具有较高的时空分辨率、成本低、效率高，以及可选择不同流动参数等特点[3]，被认为是最适合城市微气候研究的方法之一.

通常CFD数值模拟是采用足尺模型去分析实际的微气候问题[4-6]. 足尺模型由于尺度较大，计算网格数量会达到千万级别，计算开销大且效率不高. 对此，提高数值模拟计算效率的方式，一方面是对算法进行优化，另一方面就是对模型进行简化. 例如，根据相似理论建立缩尺模型进行计算[7-11]，可以保持现象的整体相似及整体信息，同时因为模型尺度的缩小使得计算网格可以合理减少，从而提高了计算效率. 缩尺模拟在计算流体力学领域也有所发展[12-18]，研究者多根据实际流动的特点分析出主要的相似准则以指导相似模拟，模拟结果可以与原型维持良好的相似性. 例如，文献[12]通过控制阿基米德数相等的原则对室内热环境问题进行了模型实验，结果表明模型的模拟结果能够较好地还原到原型中. 文献[13]在研究隧道通风问题时通过控制弗劳德数Fr相等的原则保证了缩尺模型与原型受浮力驱动的湍流的相似性，结果也验证了缩尺模拟方法的可行性. 在建筑风环境方面，有学者针对尺度较大的建筑物建立缩尺模型去验证缩尺模拟的可行性. 文献[16]对CAARC(Commonwealth Advisory Aeronautical Research Council)标准模型进行了缩尺模拟，但其模型的建立方法仅是对涉及到尺度的物理量按照一定的缩尺比缩放，流动介质仍采用真实介质，这样实验结果势必与实际相去甚远.

本文利用相似理论推导了中性大气流动的相似流动要求以及对应的边界条件，通过严格控制缩尺模型和足尺模型相似准则一致性的原则，构筑了以虚拟流动介质为基础的CFD缩尺方法，以住宅小区为原型，建立了足尺模型与缩尺模型进行数值模拟并对两者的流动形态以及具体位置的变量做了对比分析，以判别CFD缩尺模拟方法的可行性及准确性.

1 CFD缩尺模拟方法

1.1 相似要求

中性大气流动可由以下雷诺平均控制方程组描述. 连续方程为

动量方程(Navier-Stokes方程)为

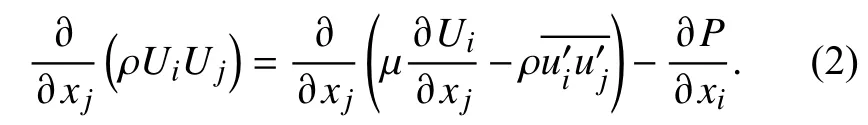
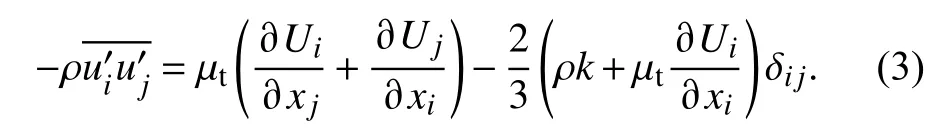
式中， µt是湍动黏度，µt∝ρul，即湍动黏度与湍流运动特征速度u和特征长度l成正比；k是湍流动能；δij是克罗内克函数(Kronecker delta).

将模型(Q′) 与原型(Q)的各物理量的相似比记为CQ， 则有：

式(4)中L表示建筑物尺度. 将式(4)代入方程(1)和(2)，则有

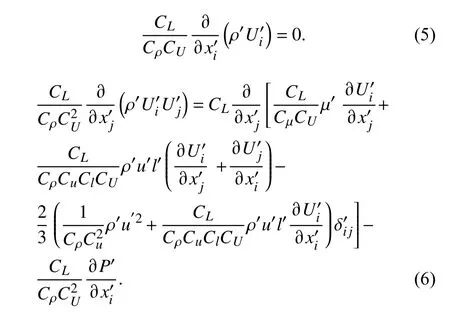
简化上式得：

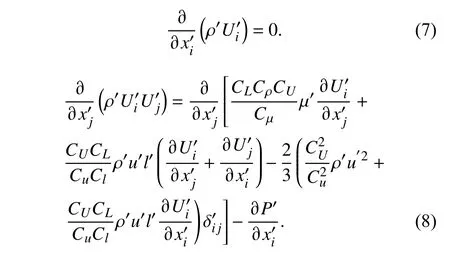
对于相似流动，以上各相似常数组合量均应等于1，即

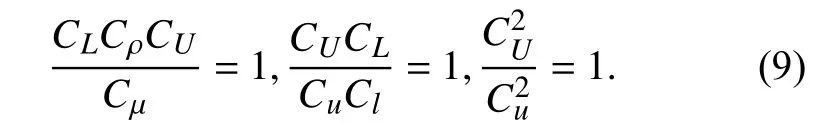
将相似变换式(4)代入式(9)，可得3个相似准则：

式(9)～(10)给出了中性大气条件下原型流动与模型流动之间的3个相似要求：(1) 平均运动的惯性力与黏性力之比保持不变；(2) 平均运动的惯性力与涡黏力之比保持不变；(3) 单位质量的平均运动动能与湍动能之比保持不变.

1.2 虚拟流动介质构筑方法

从式(4)和式(9)可以看出：相似流动由CL、CU、Cρ、Cµ、Cu以及Cl等6个相似常数决定，且各相似常数之间需满足式(9)所给出的相似关系. 因此，在缩尺模拟中可以预先给定CL、CU以及Cρ(或Cu)等3个相似比，其余相似比由式(9)确定. 例如，在本文的缩尺模拟中，取CL=1/4、CU=1和Cµ=1，根据式(9)可以确定：Cu=CU=1、Cl=CL=1/4，Cρ=Cµ/(CLCU)=4.

值得注意的是由以上方法所赋予的模型流动介质的物性(流体密度ρ 和动力黏度µ)可能与真实流动介质不相匹配，故称为“虚拟流动介质”. 将虚拟流动介质用于缩尺模拟的意义在于可以严格满足相似要求，虚拟介质本身在模拟过程中只是起到桥梁作用，足尺现象则由相似变化关系直接从缩尺模拟结果中获得.

1.3 相似流动边界条件

根据相似理论，缩尺模型和足尺模型满足相似性需要保证边界条件相似. 对于中性大气流动，其流动相似边界条件同样需要满足式(9)给出的相似要求. 这意味着对于入流边界，在足尺模型和缩尺模型之间应维持对应位置上平均风速等于给定的速度比CU、湍流强度相等以及湍流积分尺度等于给定缩尺比CL.

2 算例及分析

为了验证缩尺模拟的可行性，通过对比中性条件下建筑群周围大气流动的足尺模拟与缩尺模拟结果，从模拟的真实性、精确性和有效性等方面进行了研究分析.

2.1 计算模型及模拟过程

足尺模型中建筑物群为2×2阵列分布，各建筑物尺寸均为L×B×H=20 m×20 m×40 m(L为长度，B为宽度，H为高度)，建筑物间距为W=20 m；为了比较需要，在建筑群流动区域布置了14个采样点，计算模型及采样点如图1所示. 图2为计算域示意图，入流边界设置在建筑群迎风面前5H处，出流边界设置在背风面后20H处，测流边界设置在距离建筑最近墙面3H处，计算域顶部边界离地5H.

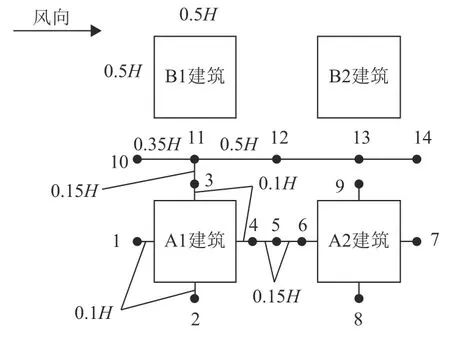
图 1 计算模型及取样点平面位置Fig.1 Computational model and sampling points

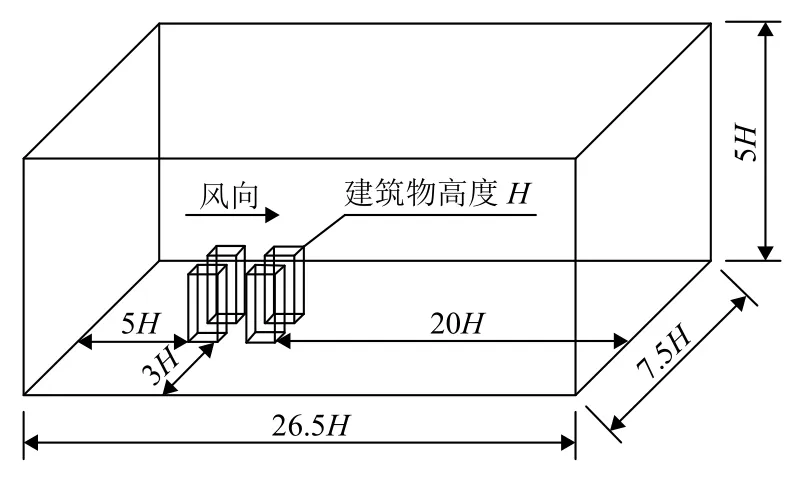
图 2 计算域示意图Fig.2 Computational domain

缩尺模型的尺寸则根据足尺模型以缩尺比CL=1/4缩小.

计算域采用的是以四面体为主的非结构化网格划分方式，足尺模型与缩尺模型网格划分对比如表1所示，网格数之比约为1:0.49.

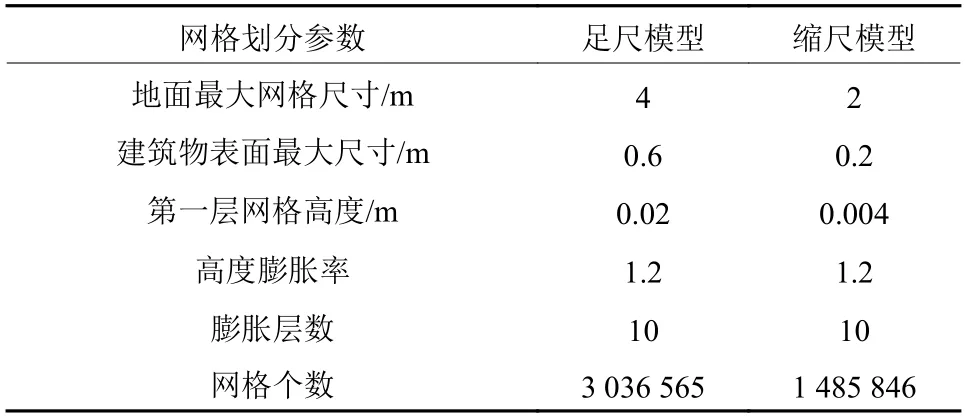
表 1 足尺模型与缩尺模型网格划分对比Table 1 Parameters of discretization

缩尺模拟流动介质的物理性能参数由1.2节给出的虚拟流动介质构筑方法确定，其与足尺模型物性参数对比如表2所示.

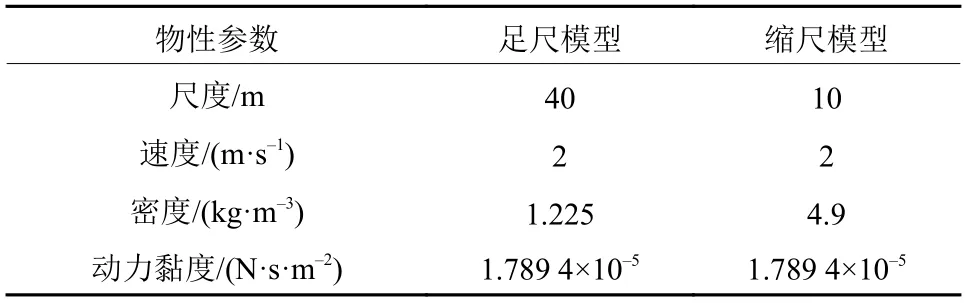
表 2 足尺模型和缩尺模型物性参数对比Table 2 Parameters of physical property

湍流模拟采用为SSTk-ω模型，边界条件设置如表3. 其中足尺模型的入流边界条件为Dirichlet边界条件，包含了平均风速剖面和湍流剖面.

平均风速剖面为

式(11)中，UH表示建筑高度来流风速，取2 m/s；α 为粗糙度系数，对于地面粗糙度类别为D类取0.22，x、y、z表示空间坐标方向.

湍流剖面为

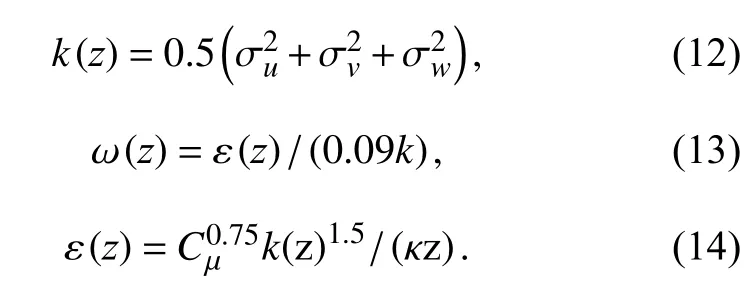
式(12)～(14)中，k是湍流动能，ω是湍流频率，ε是湍流动能耗散率；速度分量=I2(z)U2(z)；σv=0.86σu，σw=0.45σu；当z＜5 m 时，湍流强度I(z)=0.31；当z≥5 m时，湍流强度I(z)=；zg为梯度风高度，取450 m；Cµ取值0.09；κ 为开曼常数，取0.4；u、v、w表示矢量3个方向.

足尺模型与缩尺模型之间入流边界条件需要满足相似边界条件，则缩尺模型的入流边界条件如下.

平均风速剖面为

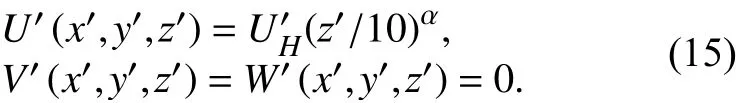
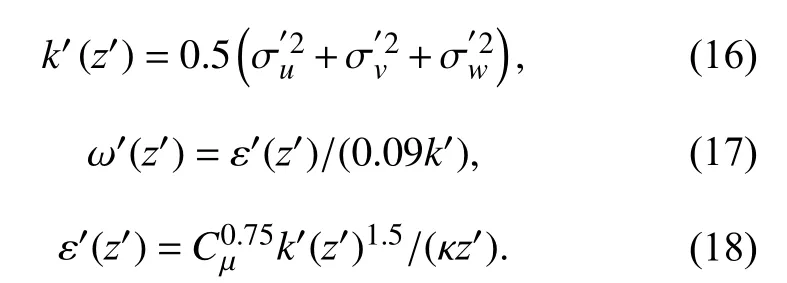
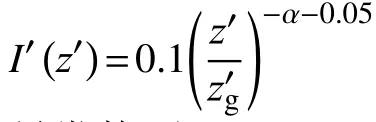
解的收敛控制设置：各求解变量的残差小于10-4，在求解域内整体不平衡小于5%.

表 3 足尺模型和缩尺模型的边界条件和模拟参数设置Table 3 Boundary conditions and simulation parameters

2.2 模拟结果与分析

2.2.1 流动形态分析

足尺模拟和缩尺模拟的竖向流动特征分别如图3(a)和图3(b)所示. 对比发现足尺流动与缩尺流动之间在气流的分离、再附特征以及特征涡旋形态特征等均一一对应. 特别是建筑物之间的2个反向旋转的漩涡结构以及后排建筑物背风面的回流腔区在大小和形态上几乎完全相似.

足尺流动和缩尺流动的平面流动特征分别如图3(c)和图3(d)所示. 对比发现缩尺模拟很好地再现了足尺流动的巷道效应、绕流特征和回流腔区等流动形态，风速场的分布特征也与足尺流动非常相似.2.2.2 模拟精度分析

图4比较了缩尺模型与足尺模型之间在采样点CρCρ=2P/ρ的模拟结果，因为这2个采样点分6和采样点11在不同高度处的平均风速和风压系数别位于低风速和高风速区，最有代表性.

图 3 足尺模型缩尺模型的流动形态特征比较Fig.3 Comparison of the flow patterns

从图4(a)和图4(b)中可看出：缩尺模拟的平均风速竖向剖面与足尺模拟结果基本吻合，较大的误差出现低风速的采样点6，其相对误差约为20%；而在高风速区采样点11误差则非常小. 比较图4(c)和图4(d)中可看出在低风速区风压系数的相对误差也较大，约为20%；同样在高风速区精度则很好. 产生以上误差的原因可能是所采用的SST湍流模型是高雷诺数模型在低风速区表现相对较差所造成的. 这意味着较高的雷诺数可以提高相似模拟的精度.

2.2.3 计算效率分析

图 4 足尺模拟与缩尺模拟精度比较Fig.4 Comparison of the accuracy

由表1可知，缩尺模型的计算网格数量约为足尺模型的50%，可以有效地减少对计算机内存的占用.在相同配置计算机平台和Fluent 15.0软件条件下，2个模型都计算800步，足尺模型的计算时长约为150 min，而缩尺模型的计算时长约为60 min，计算时间是足尺模型的40%. 结果表明缩尺模型与足尺模型相比，能够有效地提升计算效率，减少计算开销.

3 结论

本文从中性大气流动的雷诺平均控制方程组出发，用方程推导法得到了相似流动需满足的相似准则，通过保证同名相似准则一致性的原则推导出缩尺模型相似流动的边界条件和虚拟流动介质的物质参数进行数值模拟，并对足尺模型和缩尺模型的流动形态以及具体位置的变量做了对比分析. 结果表明CFD缩尺模拟方法所建立的缩尺模型能够完整地再现足尺模型的流动形态，同时保证了良好的模拟精度，从而验证了CFD缩尺模拟方法的可行性，并达到了减少计算网格数量，有效地减少计算开销的目的.