基于局部粒子群算法的家庭用电负荷优化控制策略
吴丹琦,赖俊升,2,杨俊华,李学聪,赖来利,熊锋俊
(1. 广东工业大学 自动化学院, 广东 广州 510006;2. 英国利兹大学 工程学院, 西约克郡 利兹 LS2 9JT)
智能电网在用户侧延伸的家庭能源管理逐渐成为学术界的热点. 家庭能源管理系统(Home Energy Management System, HEMS)[1-2]可实现以用户自行合理规划的智慧用电方式取代传统用电方式的目的.管理好家庭能源的重要作用是根据价格信号控制家庭用电负荷, 同时解决用电高峰时期电力供应压力大而用电低谷时期能源利用效率较低的问题.
在家庭智能用电领域的研究, 目前国外学者大多将实现用电成本最低作为调度目标, 激励用户主动改变用电习惯. 文献[3]提出购电开支最低模型, 通过确定负荷的实际工作开始时间以最大程度在低电价时段多完成用电任务. 文献[4-5]研究了动态电价机制下实现空调系统的用电费用最小化策略. 文献[6]提出在分时电价的不同时段, 监测家庭负荷的用电量以激励用户改变高耗能的用电行为. 文献[7]将一天划分为24个时间段并对各类家用负荷进行分类, 以减少购电开支.
我国于2009年首次提出“坚强智能电网发展纲要”[8], 居民智能用电是建设重点, 各项研究中优化调度算法是HEMS的核心. 文献[9]提出的家庭能源调度策略是利用二进制粒子群算法对分布式发电模块、家电优化调度模块和储能模块所组成的3种智能模块进行优化调度. 文献[10-12]分别采用非线性最小二乘法算法、动态规划算法和禁忌搜索算法对HEMS进行优化, 达到最大化用户舒适度和最小化购电成本的目的, 但这些算法对既有离散值又有连续值的混合目标优化效果不佳. 文献[13]提出的家庭用电负荷调度算法忽略了引入分布式新能源发电.文献[14]采用的是分支界定调度算法在HEMS中收敛速度快, 但存在早熟收敛且难以跳出局部最优的缺陷. 同样地在HEMS中应用广泛的粒子群算法, 往往也存在早熟收敛问题, 若某粒子发现一个当前最优位置且为局部最优解, 其他粒子将向其靠拢并难以重新进行搜索.
为避免传统粒子群算法易使家庭电能总花费陷入局部最优的缺点, 本文使用了改进后的粒子群算法——局部粒子群算法,在Python平台上进行编程和模拟仿真, 制定出家庭用户在分时电价政策下采取可控制用电负荷的智能用电策略, 实现减少电费的目的. 同时评估所用算法在优化控制策略中的效果及仿真实验中的性能, 分析验证了局部粒子群算法的有效性及实用性.
1 家庭用电负荷分析
本文根据家庭用电负荷的工作模式和储能方式等特点分为4类, 建立负荷模型.
1.1 无储能不可控负荷
无储能不可控负荷(Uncontrollable Load without Storage, 简称ULWS): 不可储存能量且工作时间不可转移, 即用户有需求必须工作. 常见的有照明类、娱乐类、烹饪类等设备.
1.2 无储能可控负荷
无储能可控负荷(Controllable Load without Storage, 简称CLWS): 不具备储存能量的能力, 工作时间可进行转移, 但一旦开始工作就不可中断. 常见的有洗衣机等清洗类设备.
本文的研究对象是拥有多种家用负荷的单个家庭, 设每个负荷设为a, 把不可中断负荷的集合记作Auni, 可中断负荷的集合记作Aint. 引入辅助变量ua(t)呈现其运行状态, 当该值为0时表示关闭, 而为1时则表示开启. 设Ea(t)为该类负荷a在t时段消耗的电能,PaN为其额定功率. 则在时间间隔Δt内有
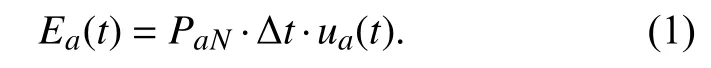
无储能可控负荷ACLWS在t时段的总能耗ECLWS(t)等于该类负荷a在t时段的电能的总和:
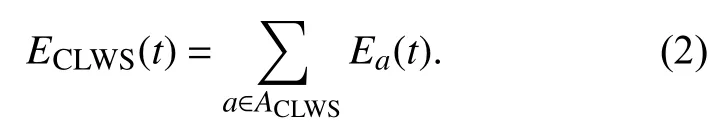
用 αa和 βa分别表示负荷a允许工作范围的开始时段和结束时段, φa为负荷a的最大延迟时段数, 若不可中断负荷在 τ+1时段开始工作, 至少需要连续工作µa个时段才能结束. 则有
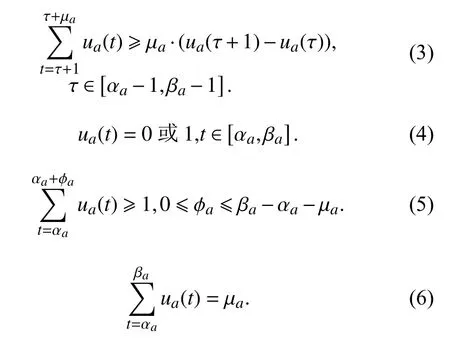
1.3 直接储能负荷
直接储能负荷(Controllable Load with Direct Storage, 简称CLDS): 在一定的时间尺度内可灵活调节电能的吸收或消耗. 目前家用分布式能源主要包括风力发电和光伏发电, 在实际应用时需要储能设备如蓄电池. 本文以带有蓄电池的家庭风力发电系统展开研究, 设PB为蓄电池的充放电功率.
1.4 间接储能负荷
间接储能负荷(Controllable Load with Indirect Storage, 简称CLIS): 可将电能转换为所需要的能量形式. 设其运行功率最大值, 则运行功率Pa需满足

本文中主要指家庭供暖、通风和空调系统(HVAC)[15]将电能转化为室内空气的冷热量,建立控制家庭室温电能消耗的动态模型[16]:
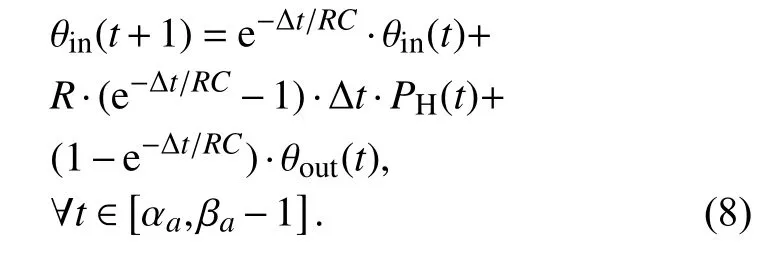
式(8)中,C为房间的热容量,R为房间的热阻,θin为室内温度,、分别为室内允许的最高、最低温度值,θout为室外温度,PH(t)为加热室内温度的功率,为室内调节功率的上限值.
在时间间隔Δt内, 当室外温度为θout(t)时, 室内温度从θin(t)变到θin(t+1), 需要的平均功率为PH(t), 则室温调节功率约束与室内温度要求分别为

2 优化控制策略模型
2.1 模型搭建
家庭能源管理系统由大电网、风力发电系统、蓄电池、家庭用电负荷构成, 由能量守恒定律可得,t时段家庭与电网的交互电能+风力发电系统的输出功=无储能不可控负荷+无储能可控负荷+直接储能负荷+间接储能负荷, 则数学表达式为
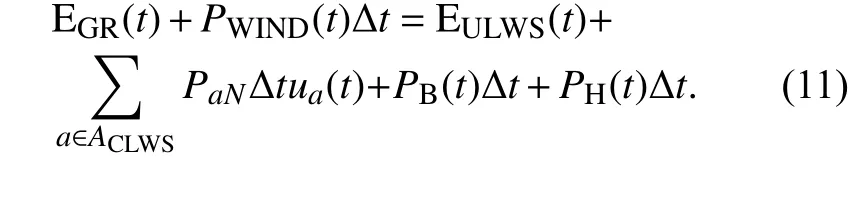
2.2 目标函数

其中,F为家庭电能总花费, φ1和 φ2分别表示fb和fc在F中的权重因子.fb为购买电能开支, prc表示分时电价,EGR(t)代表与电网的交互电能.fc(t)为舒适度成本,(t) 指用户对室温的需求设定值, Δ θ=-.
2.3 约束条件
约束条件为
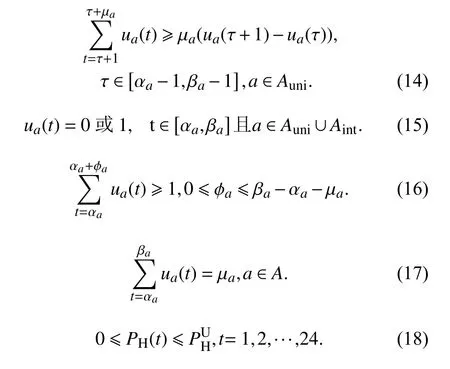
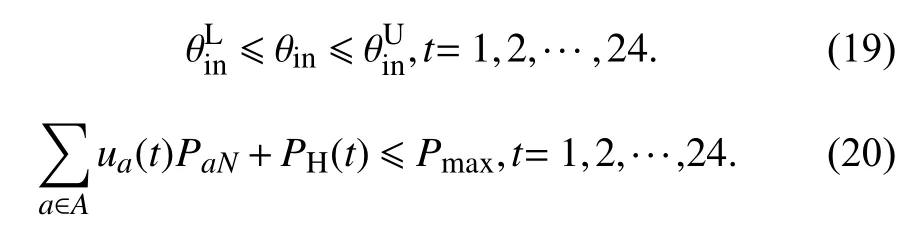
其中式(20)的Pmax代表每个家庭用电总功率的上限.
2.4 参数设置
设将一天24 h作为一个完整周期, 调度总时段为24, 则从凌晨0:00至当天晚上23:00, 对应时段依次为第1 ,2,3,···,24时段.
1) 无储能不可控负荷.
无储能不可控负荷作为固定负荷纳入用电需求, 不参与优化, 在t时段消耗的总电量为一常数, 记为EULWS(t), 其参数设置如表1所示.

表 1 无储能不可控负荷的参数设置Table 1 Parameter setting of ULWS
2) 无储能可控负荷.
无储能可控负荷的参数设置如表2所示.
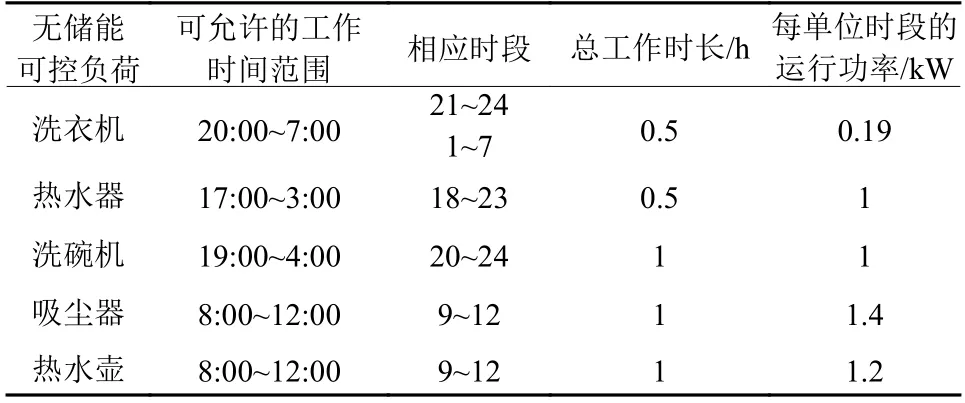
表 2 无储能可控负荷相关参数Table 2 Parameter setting of CLWS
3) 直接储能负荷.
本文研究的家庭风力发电系统, 1天内的出力情况如图1所示.
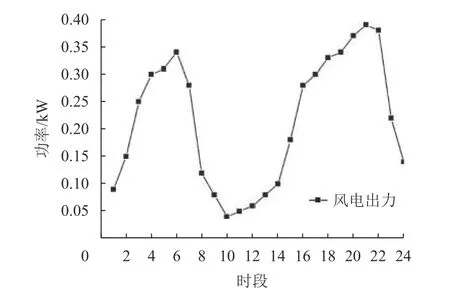
图 1 家庭风力发电系统的出力情况Fig.1 Output of home photovoltaic power generation system
4) 间接储能负荷.
间接储能负荷的参数设置为:C=0.525 kWh/℃,R=16 ℃/kWh,θinU=28 ℃,θinL=23 ℃,PHU=2 kW; 需要工作时间为18:00~8:00, 12:00~14:00, 对应时段19~24,1~8, 13~14, 时段数为16.
室外温度及室内温度需求如图2所示.
5) 分时电价.
实施分时电价可引导改善用户的不合理用电行为, 有效反映电力生产成本和供应成本. 本文以广东省广州市的居民用户峰谷平分时电价为例, 数据如表3所示.
3 优化控制策略的算法设计
3.1 算法设计的框架
图3为家庭用电负荷优化控制策略的仿真分析框架图. 图4和图5分别为无优化处理时与传统粒子群算法进行优化时的实现流程图. 传统粒子群算法(Particle Swarm Optimization, 简称PSO)[17-18]是一种随机并行的搜索算法, 模仿自然界的生物觅食过程.
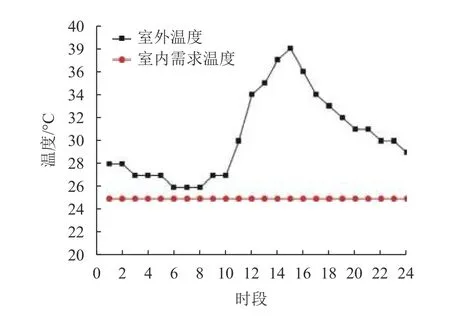
图 2 室外温度及室内温度需求曲线Fig.2 Curve of outdoor temperature and indoor temperature demand
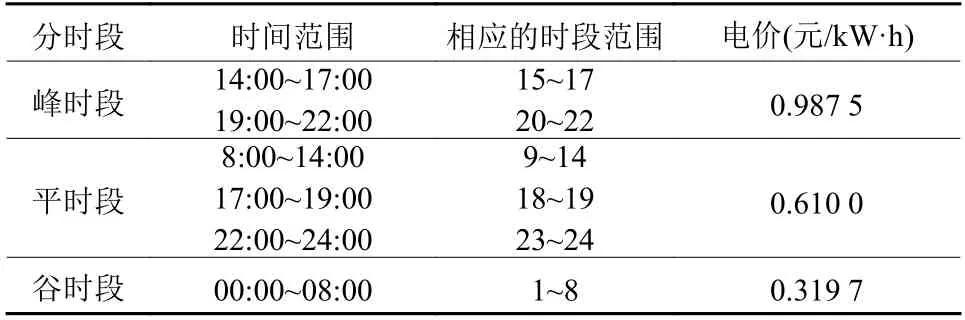
表 3 广州的分时电价数据Table 3 Time-of-use pricing data in Guangzhou
3.2 局部粒子群算法(LPSO)
为避免传统粒子群算法难以搜索到全局最优解的缺点, 在PSO的基础上, 改变粒子速度和位置的更新公式, 即将PSO的全局最优位置gbest, 变换为局部粒子群算法(Local Particle Swarm Optimization, 简称LPSO)的邻域内最优位置lbest. LPSO的优化流程图如图6所示, 实现的具体过程如下:
1) 粒子编码.
2) 初始化粒子群.
本文在21维解空间中随机产生250个粒子, 并初始化其速度和位置.
3) 评价种群: 计算每个粒子的目标函数值F(xi(t)).
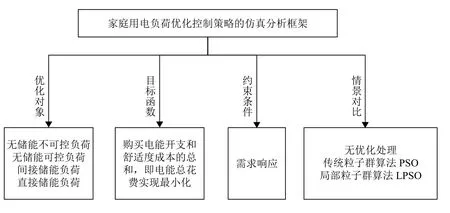
图 3 家庭用电负荷优化控制策略框架图Fig.3 Framework diagram for optimal control strategy of household electricity load

图 4 无优化处理的实现流程图Fig.4 Flowchart of no-optimization treatment
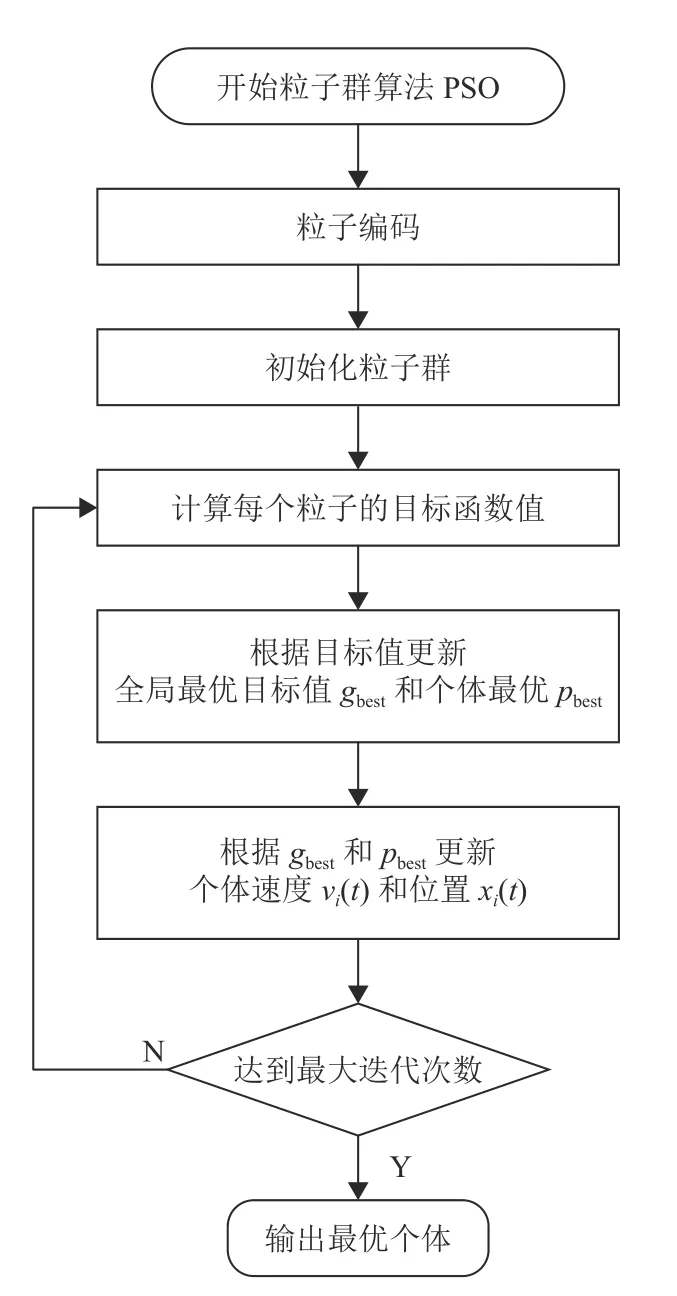
图 5 传统粒子群算法的实现流程图Fig.5 Flowchart of conventional particle swarm optimization
4) 通过闵可夫斯基距离, 定义邻域.
通过闵可夫斯基距离(Minkowski distance)来定义邻域. 设21维解空间内, 粒子i的位置为
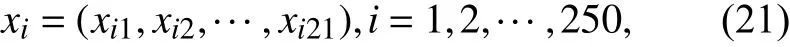
则其邻域中某粒子j的位置为
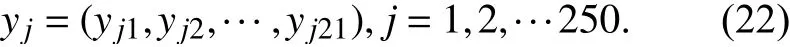
可推导得出两点之间的闵可夫斯基距离计算公式为
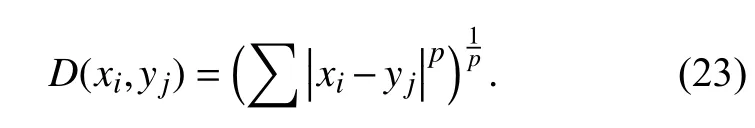
5) 通过K近邻查询法检索k个最近邻点, 得到k个lbest.
K-D树(k-dimensional tree)是一种在k维空间中划分数据点的结构, 本文所采用的K近邻查询法可检索在K-D树中与待查询点距离最近的k个数据点, 即为最近邻点. 执行步骤如下.
(1) 构建一棵K-D树.
首先统计所有待查询点在每个维上的方差并选出最大值, 对应的维就是split域的值. 然后待查询点按其第split维的值排序, 在位于正中间的点nodedata处垂直于轴的超平面将空间分割为两个子空间若空间中某个待查询点的第split维数据大于nodedata, 则属于该节点的右子空间, 若小于则属于左子空间. 最后进行递归操作直到每个子空间都不能再划分为止.
(2) 利用K-D树进行K近邻查询.
首先从父节点开始一路向下访问, 直至达到最末结点时, 计算待查询点与最末结点上保存的数据之间的距离, 记录下最小距离及其对应的数据点, 记为当前最近邻点. 然后回溯搜索路径, 判断该查询点与未被访问过的子空间之间是否存在距离小于历史记录的最小距离, 若找到更近的数据点, 则更新为当前的最近邻点及其最小距离.
6) 更新学习样本.
最近邻点的目标值即为邻域最优位置lbest.
首先比较每个粒子i的当前目标值与pbest对应的目标值, 如果F(xi(t))>F(pbest), 则pbest=xi(t); 再对比pbest的目标值与邻域内历史最优lbest的目标值, 同理,如果F(pbest)>F(lbest), 则lbest=pbest.
7) 更新粒子的速度和位置.
粒子更新速度和位置的公式中, PSO的gbest改为LPSO的lbest, 因此速度更新和位置更新的公式分别为
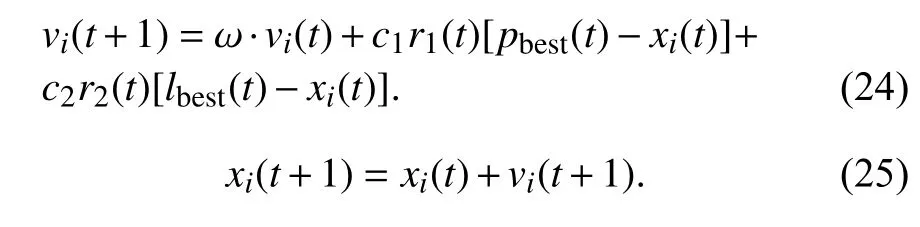
式中,vi(t+1)和xi(t+1)分别为粒子第t次迭代更新后的速度和位置,pbest(t)为粒子i第t次迭代时的个体历史最佳位置,lbest(t)为第t次迭代时的邻域最佳位置.r1(t)和r2(t)是在区间[0 1]的两个随机数. ω为惯性权重, 表示前一次的速度对当前速度的影响.c1和c2分别为个体认知因子、社会认知因子, 分别表示每个粒子向pbest和lbest运动的权重, 注意在LPSO中, 需加强社会认知经验在粒子运动中所起的作用, 即通过调大c2来加快找到邻域最优解.
8) 迭代终止判断.
当迭代次数达到预设最大值时, 输出结束时邻域最优个体的位置, 否则返回步骤(3).
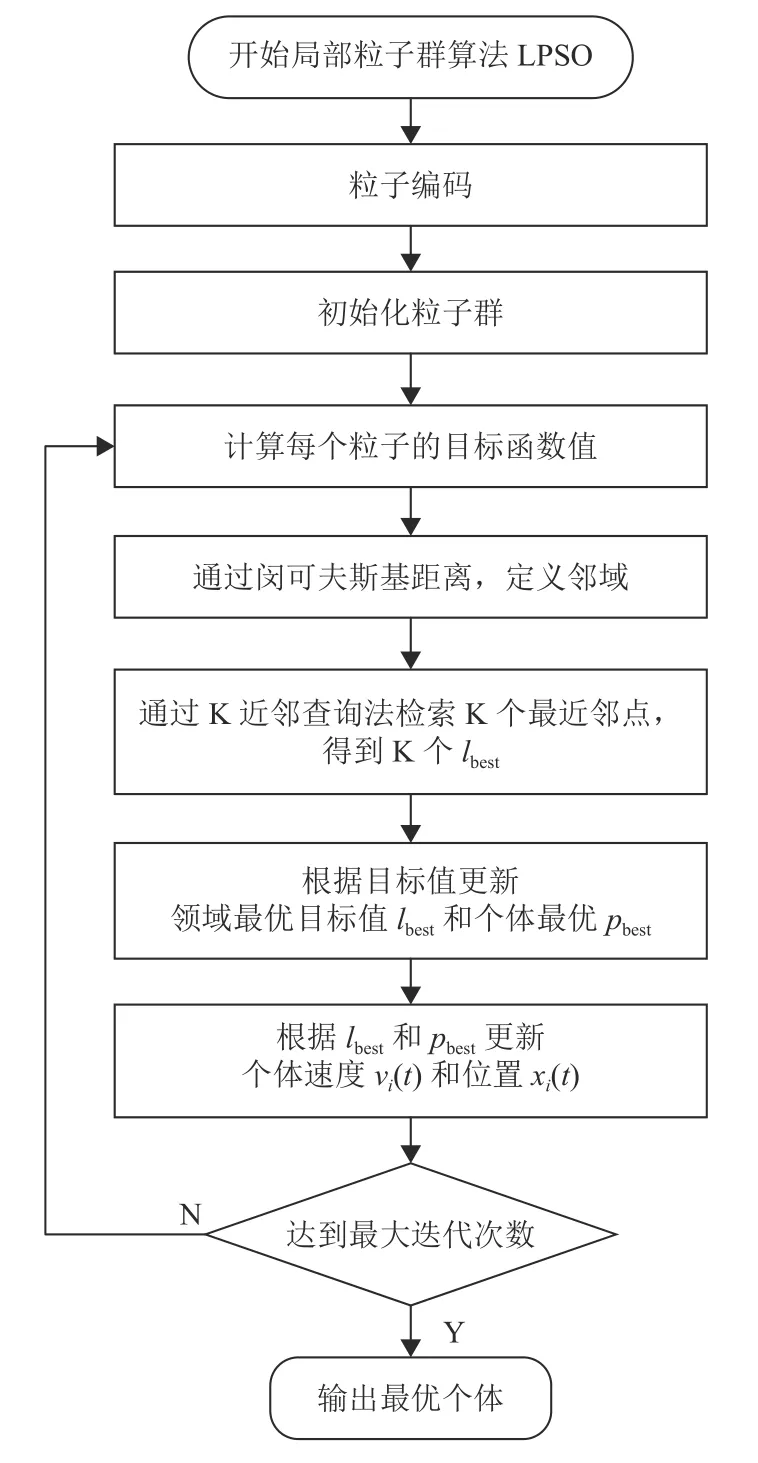
图 6 局部版本粒子群算法的优化流程图Fig.6 Flowchart of Local Particle Swarm Optimization
4 仿真结果及分析
4.1 电费最低策略的仿真结果
不同算法优化下4类负荷总电费的仿真结果如表4所示. 目标函数为家庭电能花费最少. 无优化处理、PSO和LPSO优化的总电费分别为10.81、10.28和10.05元. 因此在PSO的基础上, 结合本文的数学模型对PSO改进后得到LPSO, 增强了全局搜索能力.LPSO优化下总电费相较于无优化处理时减少约7.00%, 有效降低了电费, 且优于传统PSO算法. 对于无储能可控负荷, 相较于无优化处理时, 使用算法后电费有所减少, 说明在原始用电布局上, 家庭用电负荷进行了转移. 对于直接储能负荷, 电费以负数呈现,说明该类负荷可以产生电能满足自身所需, 减少电能总花费, 且缓解可再生能源的消纳问题. 对于间接储能负荷, 无优化时电费为5.74元, PSO优化后为5.34元, 而LPSO优化后为5.11元, 说明LPSO的优化效果良好.
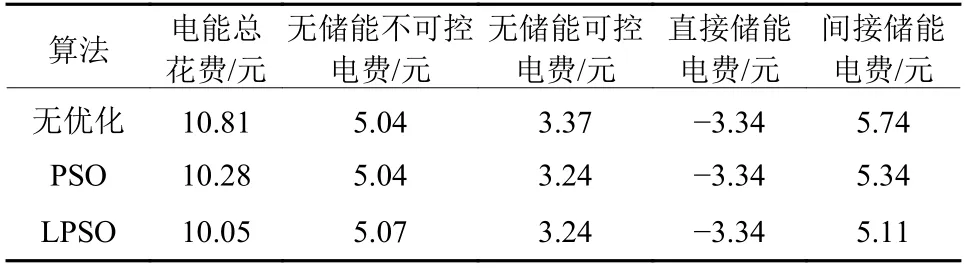
表 4 4类负荷的总电费对比Table 4 Comparison of total electricity charges using different algorithms
4.2 优化算法性能分析
不同优化算法的迭代曲线如图7所示. 对比分析, 可得:
(1) 传统PSO在达到收敛点之后与无优化处理时的目标函数值相同, 说明陷入了局部最优, 未能搜索到全局最优解, 而LPSO尽管在迭代次数60代左右时出现局部最优解, 但在130代左右目标值再次急速下降并达到稳定, 证明也找到了邻域最优解(实质也是全局最优).
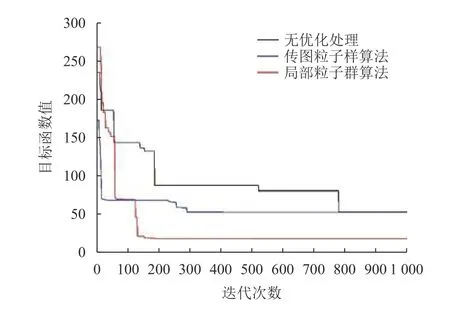
图 7 不同优化算法的迭代曲线Fig.7 Iterative curve of different optimization algorithms
(2) 设置动态惯性权重或者动态认知因子, 结果都是收敛速度很快, 但容易陷入早熟收敛, 且后续无法跳出局部最优, 故效果均不理想. 而将全局最优位置改为邻域内最优位置的LPSO最终搜索到全局最优解, 证明了改变拓扑结构的局部算法适合本文优化目标.
(3) 目标值随着迭代次数的增加而逐渐降低, 由迭代曲线图可得在迭代次数达300次之前, PSO和LPSO都已搜索到最优解, 且目标值不再变化, 因此在实际应用中, 如果计算资源过少或调度时间较短,可以适当减少最大迭代次数.
4.3 家庭智能用电方案
在减少电费和收敛到全局最优解这两方面,LPSO都拥有比传统PSO更优越的性能, 因此可选择LPSO优化下的家庭智能用电方案.
无储能可控负荷的控制方案如表5所示, 家庭用户可据此提前设定洗衣机、热水器、洗碗机、吸尘器、热水壶这五种负荷的启动工作时间. 表6给出了使用LPSO进行优化时, 整个控制周期内间接储能负荷的用电控制方案, 即各个时段HVAC所需的功率.
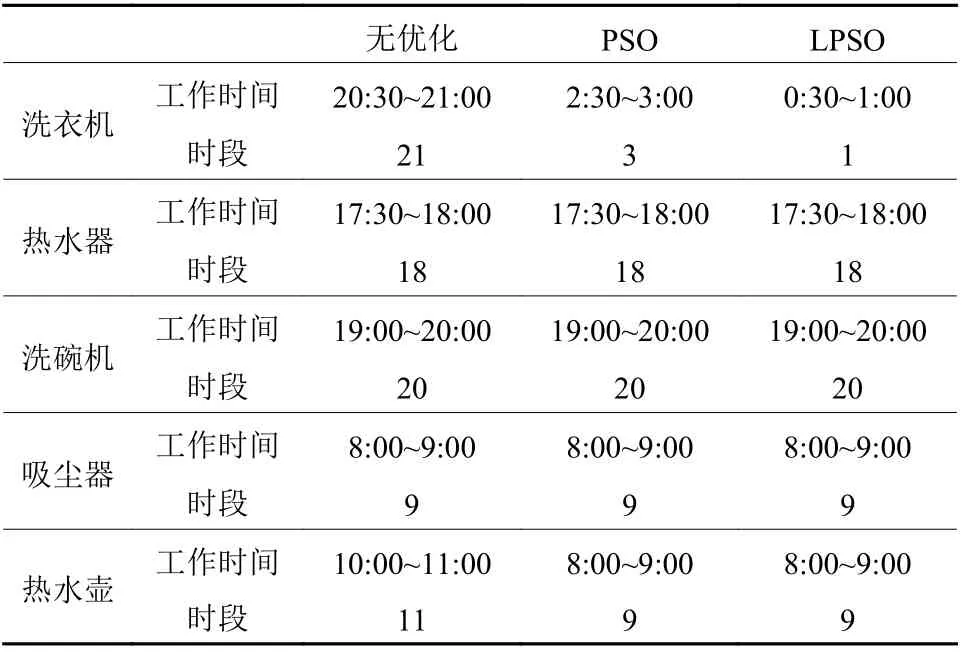
表 5 无储能可控负荷的控制方案Table 5 Control scheme of CLWS

表 6 LPSO优化时HVAC的控制策略Table 6 Control scheme of HVAC using LPSO
5 结论
综合评估在制定家庭用电负荷优化控制策略中减少电费的效果, 以及在迭代曲线上呈现的是否能收敛到全局/邻域最优解, 可得出结论: 局部版本粒子群算法拥有比传统粒子群算法更好的性能, 可推广应用到家庭能源管理领域的相关研究, 其优势在于LPSO在家庭用电负荷优化控制中降低家庭电能总费用的效果显著, 且可有效解决传统PSO全局最优搜索能力不强的问题.

