基于瞬时频率的FSK信号解调研究
王雪丽
摘 要:比较常用的FSK信号解调方法有频率推算、相位推算,可以解调出信号的两个频率,用FFT和ZFFT检测信号的调制频率,此方案的缺点是只有在信噪比较高时才能达到精度要求。文章研究了一种新的解调方案,把希尔伯特-黄变换算法引入到FSK信号的解调之中。通过改进算法,只需用IMF1(第一个本征模态函数)的瞬时频率即可检测出FSK信号的载频和调制频率。仿真结果显示,即使在信噪比为1∶3甚至更低的情况下,希尔伯特-黄变换算法的解调精度仍然高于以往的算法。
关键词:频移键控;希尔伯特-黄变换;瞬时频率
1 频移键控调制定方法产生背景
随着无线通信技术的不断发展,人类对通信的要求越来越高,但是有限的带宽却成为人类目前无法克服的现实障碍。经研究发现,增大信号的调制阶数可以提高带宽的利用率,在有限带宽内传输更多的信息,但这样做的后果是解调的误码率显著提高。所以,在增大调制阶数的同时控制解调误码率,研究新的解调方法势在必行。目前常用的通信调制方法有频移键控(Frequency Shift Keying,FSK)、相移键控(Phase-Shift Keying,PSK)、正交振幅调制(Quadrature Amplitude Modulation,QAM)等,不同的调制方法适用于不同的通信场合。FSK调制是信息传输中使用较早的一种调制方式,优点是容易实现,具有较好的抗噪声和抗衰减性能。通常情况下,它的载波是正弦波的形式,调制波是阶梯信号的形式,比如2FSK信号调制波是方波。我国最常见的FSK信号是轨道信号[1],无论是国产轨道信号,还是从国外引进的ZW2000信号都属于FSK信号[2]。基于FSK信号使用广泛性及解调的重要性,本文将详细讨论基于瞬时频率的FSK信号的解调算法,为FSK信号的解调提供可行性方案。
2 2FSK信号产生原理
想对FSK信号解调,就必须了解FSK信号的调制原理。以2FSK信号为例,它的调制信号是一个占空比为50%的方波信号,处于方波高电平处的信号为载波1,处于方波低电平处的信号为载波2,载波1与载波2的频率不同。所以,最终形成的2FSK信号波呈现的是,两个不同频率的正弦载波随着方波高低电平的交替而交替显现,且相邻两个载波在相位上是连续的。因此,对2FSK信号解调需要正确解调出低频调制信号和载波信号。轨道FSK信号属于2FSK信号,为了保证火车安全运行,必须正确解调出其上、下边频和携带火车速度信息的低频调制信号。
5 瞬时频率解调FSK信号的算法实现
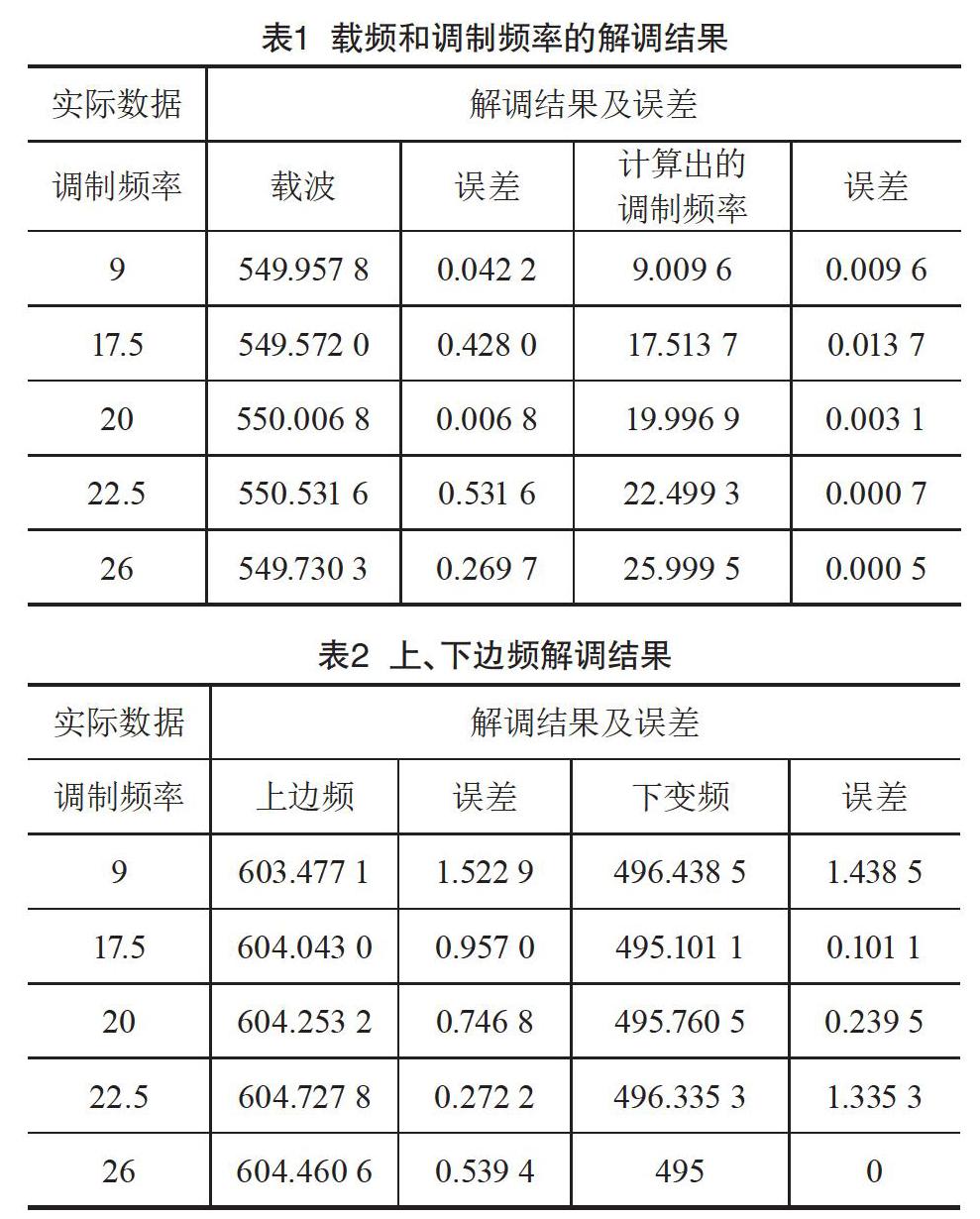
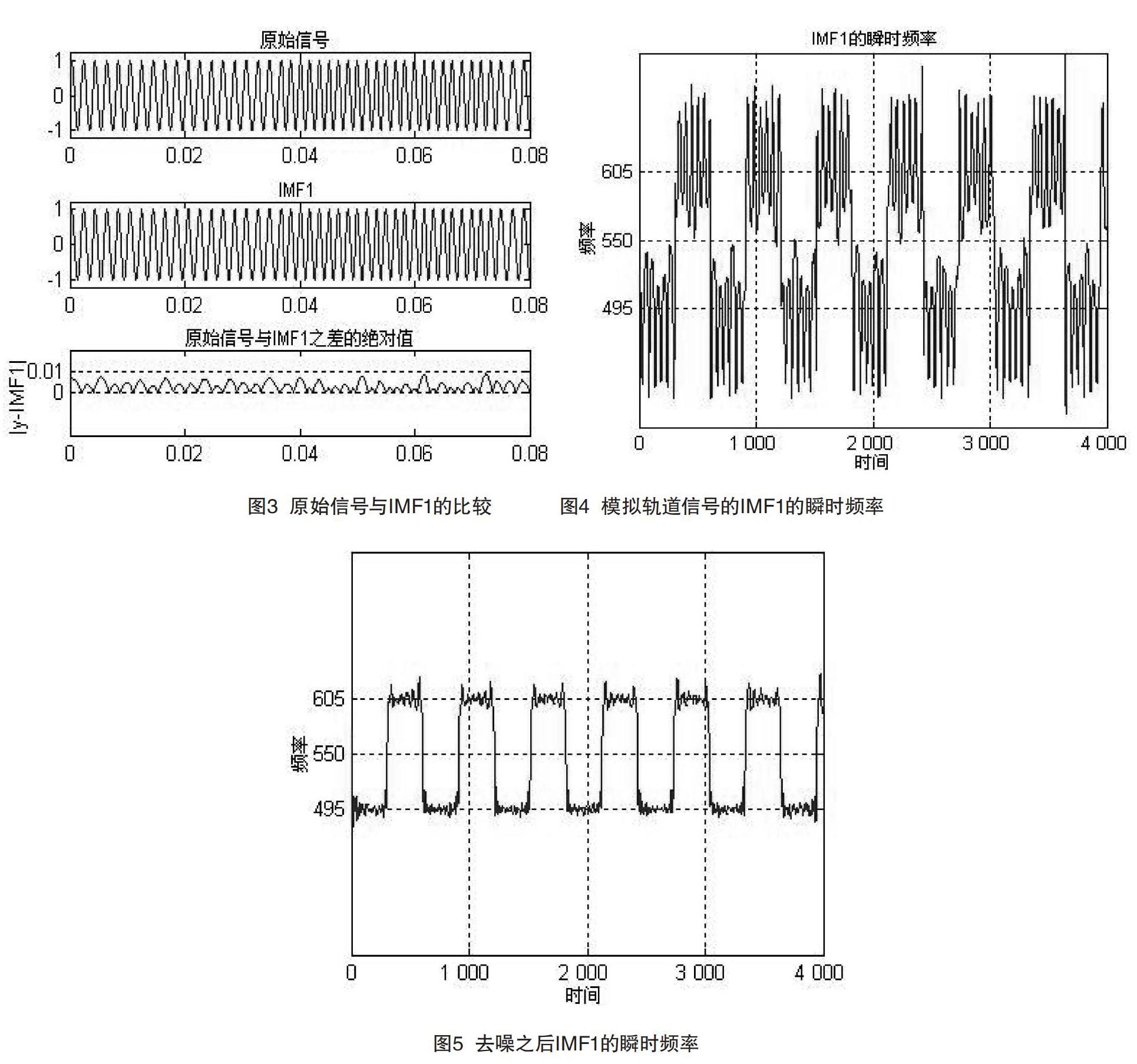
本文用Matlab仿真此算法。首先,用EMD法对FSK信号进行分解,将得到若干个IMF分量,由HHT的概念可知,第一个IMF分量(记为IMF1)的频率最高。其次,经过Matlab分析计算FSK信号与各IMF分量的绝对误差发现,IMF1分量与FSK信号的误差最小,不到0.01,原始信号加入噪声后进行EMD分解所得到的IMF1的瞬时频率。如图3所示。由此可以推测,对于不含噪声的信号而言,IMF1分量几乎包含了原始FSK信号的所有特征。实际应用中的FSK信号是含有噪声的,为了证明HHT具有解调实际FSK信号的可行性,本文以轨道信号为例,用Matlab模拟实际轨道FSK信号,并对此信号进行了EMD分解,进而得到IMF1。如图4所示,可以观察到它仍然能够体现出FSK信号的特征。如果在EMD之前对含噪信号进行去噪处理,效果会更佳,如图5所示。
经过大量的算法分析,最终总结出了用瞬时频率解调2FSK信号的算法,如下所述。
5.1 求解2FSK信号的两个载波的频率的算法
用HHT算法分解2FSK信号得到IMF1分量,求此分量的瞬时频率的平均值。
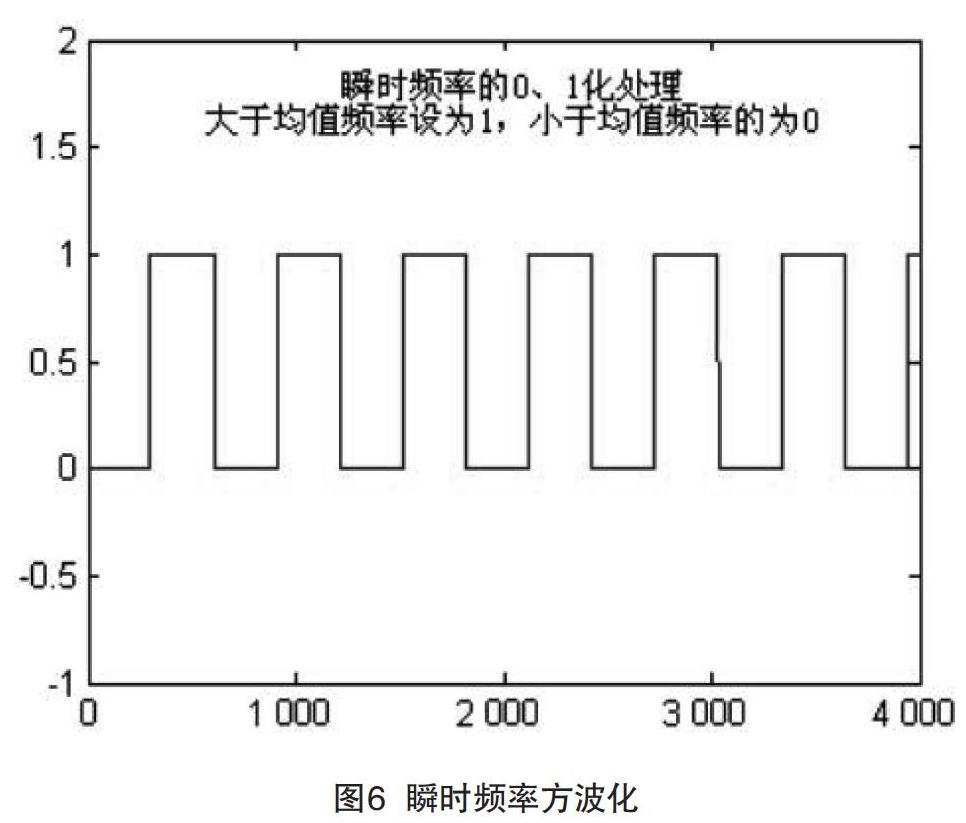
将IMF1的瞬時频率与做比较,大于的所有频率分为一组,并求其平均值F1,小于的所有频率分为一组,并求其平均值F2。F1,F2即为2FSK信号的两个载波的频率值。
5.2 求调制频率的算法
加入正弦噪声,噪声频率为450 Hz、550 Hz和650 Hz。解调结果如表1—2所示,在不去噪的情况下,信噪比为1∶3甚至更低时,直接进行解调的结果仍然非常乐观。其中上,下边频和载频的解调误差在2 Hz以内,调制频率的解调误差在0.01 Hz以内。无论是哪个误差都在误差允许的范围内,可见,瞬时频率法解调FSK信号具有很大的实用价值。
6 结语
与傅里叶变换的频域分析方法不同,HHT是一种时频分析法,它将时间和频率结合,其筛选出来的IMF分量的瞬时频率可以非常直观地显示出信号频率随时间的变化规律。经分析发现,只需用IMF1分量的瞬时频率便可解调出FSK信号的两个载频和调制频率。仿真结果表明,基于瞬时频率的FSK信号的解调精度比频域分析法几乎高出两个数量级。因此,瞬时频率解调法是一种理论上可行的解调方案,同样适用于MFSK信号的解调。
[参考文献]
[1]费锡康.无绝缘轨道电路原理及分析[M].北京:中国铁道出版,1993.
[2]冯胜,黄明.ZPW-2000轨道电路移频信号调制解调优化方法的研究[J].徐州工程学院学报(自然科学版),2018(2):72-77.
[3]NORDEN E,ZHAOHUA H,STEVEN R L.Study on instantaneous frequency[J].March,2006(49):10-13.
[4]MANDEL L.Interpretation of instantaneous frequencies[J].American Journal of Physics,1974(10):840.
[5]HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings Mathematical Physical & Engineering Sciences,1998(1971):903-995.
[6]王雪麗.基于TMS320C6720的轨道信号解调方案研究[D].北京:北京交通大学,2009.
[7]林雪玲.基于HHT改进算法的轨道信号解调设计[J].自动化与仪器仪表,2017(6):124-126.
Abstract:For FSK signal, the common demodulation method is using IFM by frequency deduction and IFM by phase deduction to acquire the frequencies, and using FFT and ZFFT to detect modulation frequency, the shortcoming of this method is it doesnt meet the need of precision until signal-to-noise is very high. This paper studies a new demodulation method. It is that apply the Hilbert-Huang Transform to demodulate the FSK signals. By improving the algorithm can detect the carrier frequency and modulation frequency of FSK signals only using the instantaneous frequency of the first IMF (intrinsic mode functions). Using this method, although signal-to-noise is the ratio of one to three or even more less, the precision is still higher than the other methods.
Key words:frequency shift keying; Hilbert-Huang transform; instantaneous frequency

