页岩气压裂弯管中液固两相流冲蚀磨损的数值模拟*
成 芳,易先中,彭 灼,周元华,宋顺平,盛治新,殷光品
(1.长江大学 机械工程学院,湖北 荆州 434000;2.中国石油集团川庆钻探工程有限公司长庆钻井总公司,陕西 西安 710021;3.青岛金江源工业装备有限公司,山东 青岛 266111;4.湖北佳业石油机械股份有限公司,湖北 荆州434000)
0 引言
管道在城市给排水、储运工程、化学工程及石油工业等各方面都发挥着重要的纽带作用。页岩气在储层上具有储层致密、渗透率低等特征,此类特征会造成页岩气开发困难,水力压裂技术是目前页岩气开发依靠的主要储层改造手段[1-2]。高压压裂液和压力管线是压裂过程工艺中的重要组成部分,压裂液中携有的支撑剂固体颗粒会随着高压高速流体流动对管线造成不同程度的冲蚀磨损,一般认为,冲蚀是流体介质携带固体颗粒并以一定的速度或角度冲击材料壁面所造成的磨损现象[3-5]。值得注意的是,冲蚀作为工业生产过程中引起材料磨损与设备失效的重要失效行为,具有突发性和危险性,磨损机理复杂,是一种极难预防的破坏形式[6]。有大量研究表明,弯管段的冲蚀磨损比直管段大约严重50倍[7]。同时,冲蚀会改变材料的性能,使得设备的剩余强度发生变化[8-9],严重时将导致管汇的刺穿、破裂等重要经济损失和设备故障[10]。
由于计算流体动力学理论、CFD技术和实验技术手段的不断更新与发展,国内外均对此有了大量的研究并取得了相应成果。易先中等[5]对同一影响因素取平均值并比较其冲蚀速率的增长倍数,认为流速是影响冲蚀磨损的主要因素;杨向前等[11]通过冲蚀磨损试验机分析得到了不同直径固体颗粒对35CrMo钢冲蚀的影响,探讨了在一定范围内的冲蚀角度与冲蚀速度时冲蚀的影响;孟杏等[12]对试样进行了冲击磨损试验,分析了冲击角度、冲蚀介质和冲击时间对冲蚀磨损量的影响;Lopez等[13]研究了颗粒速度和平均冲击角对溶解的AISI 304和淬火回火AISI 420不锈钢冲蚀的影响;Sugiyama等[14]对不同材料在钻井液90°冲击角下冲蚀后的表面轮廓进行了数值分析。总之,目前在水力压裂对弯管的冲蚀研究方面,主要集中在流体的特性参数对管壁及不同材料的冲蚀影响分析,但在现场不可避免使用不同管径的弯管,压裂液的流速也会依据工程需要进行改变。而对于不同流速与不同管径耦合时,冲蚀位置的变化及冲蚀规律尚不够清楚,因此本文将对弯管进行数值模拟分析,探讨冲蚀位置随流速与管径变化时的变化规律。
1 模型建立
1.1 几何建模及参数
本文的研究对象为JY型弯管,其基本结构尺寸是内径为D,曲率半径为A=2D的弯曲度90°圆形弯管,材质为PCrNi3Mo,建立模型进行冲蚀磨损分析。由于入口端面效应的影响,为了确保流体在管道内充分流动和流场稳定,在弯管入口段和出口段延长距离为L=5D的直管段,如图1所示为计算对象。网格采用六面体结构性网格划分方式,在弯管段进行网格加密处理,为保证更为真实准确的流体流动状态,需在管壁处设置合理的边界层。压裂液物理性能的基本参数如表1所示。
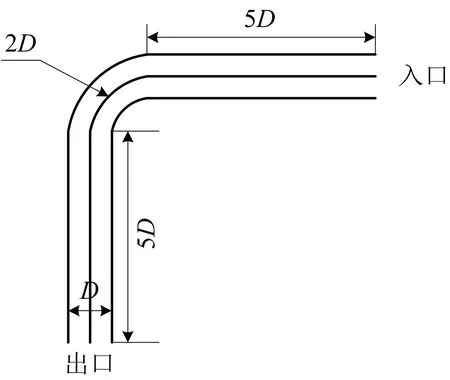
图1 弯管几何模型Fig.1 Geometric model of bend pipe

表1 压裂液物理性能基本参数Table 1 Basic parameters for physical properties of fracturing fluid
1.2 计算模型的建立
水力压裂过程中,压裂液在快速流经弯管时,管道内部流体为复杂的液-固两相三维紊流流场。因所计算的压裂液支撑剂固体颗粒体积分数小于10%,故对弯管的冲蚀数值模拟选用DPM模型。其中,连续相为压裂液流体,离散相为压裂液支撑剂颗粒,由于颗粒体积分数小,可忽略颗粒间的相互作用,从而满足颗粒负载流动模式。并在Eulerian坐标系下求解连续相流体的流场,在Lagrangian坐标系下计算离散相固体颗粒的运动轨迹方程。管内部三维紊流流场的数值模拟采用标准k-ε方程模型。为了进行弯管冲蚀特性的研究,本文对分析做出如下假设:1)认为管内壁完整,不存在缺陷与凹坑;2)忽略温度变化对流体黏度的影响,不考虑重力因素对流体流速的影响;3)流体不可压缩并具有连续性,为稳定定常流动,不存在气泡,流体充满管道内部。
压裂弯管内壁面的冲蚀速率的大小与颗粒质量流量、颗粒冲击速度、颗粒粒径大小、颗粒特性等因素有关,根据文献定义[15],即:
(1)
f(θ)=2.69θ+1.61θ2-8.84θ3+7.33θ4-1.85θ5
(2)
式中:Rerosion为冲蚀速率,kg·m-2·s-1;N为颗粒碰撞数目,无因次;mp为颗粒平均质量流量,kg·s-1;C(dp)为颗粒粒径的函数,一般情况下,C(dp)=1.8×10-9;θ为颗粒对管道壁面的冲击角(入射角),(°);f(θ)为冲击角(入射角)θ的函数;v为颗粒冲击速度,m·s-1;b(v)为颗粒相对于速度v的函数,决定冲蚀快慢的重要参数,默认为2.6;Af为冲蚀壁面计算单元的面积,m2。
在运用Fluent计算过程中,进口边界条件定义为速度入口(velocity inlet),出口边界定义为自由流出(outflow),设置入口处压裂液流体与支撑剂固体颗粒的速度大小相等、方向相同,DPM模型中入口与出口均采用逃逸(Escape)类型,壁面条件为Wall壁面,在DPM模型中采用反弹(reflect)类型,反弹系数依据A.Forder和KR.Ahlert等[16-17]的研究成果取值,动能、能量、湍流耗散率的离散均选用二阶迎风格式。
2 计算结果分析
网格作为有限元计算的重要前提,网格数量的变化会导致计算结果的差异化。对所计算对象的网格进行无关性验证,文献[18]指出国际学术界认为网格变化导致计算数据变化小于2%为可取值,因此本文以弯管的最大冲蚀率的变化为界定标准,当弯管整体计算模型网格数量达到101 190时,最大冲蚀率数值变化已小于2%,计算结果满足网格无关性的基本要求。且网格平均质量高于0.8,等角斜率小于0.76,网格质量较好。
2.1 弯管的流场分析
为了分析流体携带固体颗粒在流经弯管时,管内复杂的流场变化情况。依据已确定的初始数据、边界条件及计算方法,本文选取压裂液流速为5~25 m/s,管径为50.8~152.4 mm的弯管设置合理梯度进行数值模拟分析,得到其压力场分布与最大冲蚀速率。下面将选取在入口速度在5~25 m/s,管径为127 mm的弯管进行分析说明。
从图2可以得知,在管径一定时,不论流速如何变化,在弯管段存在较为明显的压力梯度,具体分布为从弯管段的外侧区域至内侧区域,压力数值呈现逐渐减小的趋势。同时,流体流经弯管时的最大压力均分布在弯管段内壁面外侧区域,最小压力分布在弯管段内壁面内侧区域。

图2 弯管压力云图Fig.2 Nephogram of bend pipe pressure
为进一步阐述高压压裂液在流经管道时的流场特性变化情况,将从2条流动路线进行考虑分析。压裂液从“入口直管段→弯管段外侧区域→出口直管段”流动时,压力数值具体变化为“压力减小→变大→减小”;压裂液从“入口直管段→弯管段内侧区域→出口直管段”流动时,压力数值具体变化为“压力减小→减小→变大”。可以认为,流体流经弯管段时,由于离心力的作用,使得弯管段的流体由内侧区域朝着外侧区域运动,导致产生弯管段外侧压力大,内侧压力小的现象。即弯管段压力小的区域流体速度大,反之,压力大的区域流体速度小。流体进入入口直管段至弯管段处压力逐渐减小的原因为,在沿着流体流动方向有较大的沿程阻力,且在弯管段流体内侧区域向外侧运动时产生了涡流。在弯管出口至出口直管处,且由于在弯管段涡流的产生和作用,使得有局部的压力损失,即出口直管段的压力变小。
2.2 弯管的冲蚀磨损分析
数值计算结果表明,弯管中冲蚀磨损发生区域有5处,分别为弯管的入口直管段、弯管段内壁面外侧(液体进入弯管后的正对区域)、弯管段靠近出口内壁面的外侧区域、直管段靠近弯管段的侧方区域以及出口直管段。但是,在弯管的入口直管段仅有着零星状的冲蚀磨损现象发生,在出口直管段也存在着一定程度的均匀点状冲蚀磨损情况,入口直管段与出口直管段的冲蚀磨损>情况均不严重且不会随着流速等特征参数变化而产生明显的磨损程度加深和区域变大。
总体分析认为,压裂液固体颗粒对弯管的易冲蚀区域且冲蚀严重区域主要有3处,如图3所示为弯管段靠近出口内壁面的外侧区域(A区域)、弯管段内壁面外侧(液体进入弯管后的正对区域)(B区域)以及直管段靠近弯管段的侧方区域(C区域)。如图4所示是管径为127 mm的弯管在入口速度为5,15,25 m/s时的冲蚀云图。
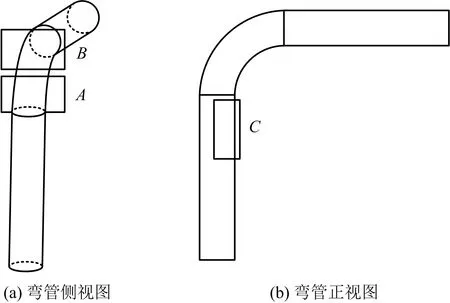
图3 弯管易冲蚀区域示意Fig.3 Schematic diagram of erosion prone area in bend pipe
值得注意的是,无论入口速度如何变化,弯管段靠近出口内壁面的外侧区域(A区域)冲蚀磨损始终较为严重,而弯管段内壁面外侧(液体进入弯管后的正对区域)(B区域)和直管段靠近弯管段的侧方区域(C区域)的冲蚀磨损情况随着入口速度变化而改变。可以这样认为,以上3处存在较大冲蚀磨损的原因在于,高压压裂液自直管段进入到弯管段后,由于弯管段存在压力梯度、离心力等作用形式,使得压裂液及大量的压裂液固体颗粒均被甩向曲率半径较大的外壁面,即颗粒由内侧朝着外侧运动,且冲击速度明显变大,造成颗粒冲击个数、壁面冲击次数明显变多,即弯管段外壁面(A区域)的冲蚀磨损较为严重。且随着流速的变大,固体颗粒撞击到壁面的速度也相应变大,即使得颗粒的动能变大,在单位时间内撞击到壁面的颗粒个数与冲击动能也有了较大的提升,使得弯管段内壁面外侧(液体进入弯管后的正对区域)(B区域)的冲蚀磨损程度加大。而在直管段靠近弯管段的侧方区域(C区域)出现冲蚀磨损的原因在于二次流的影响使得颗粒冲击到管壁侧壁的速度变大,且压裂液固体颗粒在冲击到外侧区域的壁面后,颗粒由于反弹效应撞击至弯管的侧方,使得在侧方也出现了一定的冲蚀磨损现象。
特别的,如图4所示压裂液流速从5 m/s至25 m/s时,经分析得压裂液流速的增大会导致直管段靠近弯管段侧方区域冲蚀磨损情况减弱,而与直管段正对方向的弯管段区域的冲蚀磨损范围不断变大,即并非所有弯管段的侧方区域(C区域)和直管段正对方向的弯管段区域(B区域)都会有较为严重的冲蚀磨损情况。为分析这一现象,本文将引入斯托克斯数(St)进行分析,斯托克斯数(St)是能用于度量颗粒的动量非平衡程度的无量纲量,其定义颗粒响应时间与系统响应时间之比为:

图4 弯管冲蚀云图Fig.4 Nephogram of bend pipe erosion
(3)
式中:ρd为颗粒密度,kg·m-3;dp为颗粒粒径,mm;v为流速,m·s-1;μ为流体黏度,Pa·s;D为管径,mm。
总体而言,流体携带固体颗粒从直管进入弯管区域后,固体颗粒会受到惯性力、曳力、二次流等作用力的共同作用,使得流体及固体颗粒的受力形式和运动轨迹更为复杂。所谓惯性力,是指在弯管中保持固体颗粒沿切向运动的作用力,即惯性力的作用会使得弯管在液固两相流的冲蚀磨损发生在弯管内壁面的外侧区域,且为液体进入弯管后的正对区域;而曳力是指使得颗粒沿着流体流线运动的作用力,曳力的作用下将使得固体颗粒沿着液体流线流出弯管段;二次流是指流体或颗粒偏离主流运动方向上的平均流动现象,二次流的出现更增加了弯管中流体流动和冲蚀磨损的复杂性,在该作用力下颗粒将朝着弯管内壁面的侧方区域运动,使得在该处出现冲蚀磨损现象。
由式(3)斯托克斯数(St)的定义,斯托克斯数(St)也表征着颗粒的惯性力与曳力之比,分析将综合考虑2种作用力的比值,当St<1时,即惯性力的数值小于曳力时,颗粒响应时间较短,颗粒的运动将紧跟连续相,颗粒的跟随性较好。同样的,当颗粒在弯管段中惯性力的数值小于曳力时,此时的曳力将起主导作用,使得惯性力与曳力的方向发生偏移,合力方向指向弯管段靠近出口直管段内壁面的外侧区域(A区域),大量固体颗粒向着该合力方向所指处冲击,即冲蚀磨损区域主要发生在弯管段靠近出口内壁面的外侧区域;当St>1时,即惯性力的数值大于曳力时,表示颗粒无足够响应时间来响应流速的变化,颗粒的运动将独立于连续相,即颗粒的运动受流体影响小,此时颗粒在弯管段中惯性力的数值大于曳力时,此时的惯性力将起主要作用,在惯性力与曳力的共同作用下,弯管段内壁面外侧(液体进入弯管后的正对区域)冲蚀磨损区域(B区域)的范围将变大,即在该区域会有连续均匀的片状冲蚀磨损。
而对于二次流对弯管侧方区域的冲蚀影响,本文认为应以St的具体数值进行评价,在图4中,管径为127 mm的弯管在入口速度为5,10,15,20,25 m/s时,经计算其St分别为0.334,0.688 9,1.032,1.376,1.72。可以认为,当St不断增长时,弯管侧方区域的最大冲蚀速率也不断下降,故认为,由于St的增长,流体携带固体支撑剂颗粒的能力得到遏制,无法携带大量的固体支撑剂颗粒向着弯管内侧壁面运动,即冲击弯管侧方区域壁面的固体颗粒数量有限,冲蚀磨损程度也呈现下降趋势。
同时,当St=1左右时,侧方区域的冲蚀磨损下降至几乎与出口直管段的冲蚀磨损程度相近,但无论St数值怎么上升,依据图4的弯管冲蚀云图显示,侧方区域的冲蚀磨损情况已趋于稳定。
值得注意的是,弯管段内壁面外侧(液体进入弯管后的正对区域)(B区域)与直管段靠近弯管段的侧方区域(C区域)的最大冲蚀速率及磨损区域会随着流动参数及管径等结构参数的变化而产生明显的规律性差异,2处的冲蚀磨损情况呈现“此消彼长”的情况。
2.3 管径与流速耦合冲蚀分析
由于在不同管径与不同流速等特征参数下,与之对应的最大冲蚀速率不断变化,为综合考虑管径、流速与最大冲蚀速率的变化,得到如图5所示的三维曲面关系示意图。

图5 不同管径与不同流速下的弯管最大冲蚀速率关系Fig.5 Relationship between maximum erosion rate of bend pipe and different pipe diameters and flow velocities
由图5可知,在任意管径下,压裂液流速的增长必然使得弯管的最大冲蚀速率呈指数关系增长。随着流速的增长,依据式(3)斯托克斯数(St)将不断变大,颗粒对弯管的最大冲蚀磨损区域将由C区域向着A区域变化。
为比较分析不同管径的弯管在不同压裂液流速下最大冲蚀速率,当管径从50.8 mm至152.4 mm变化时,经软件Origin进行公式拟合得其指数函数关系分别为:
(4)
(5)
(6)
(7)
(8)
式中:y表示最大冲蚀速率,kg·m-2·s-1;x表示压裂液流速,m/s;y1~y5分别是管径为50.8,76.2,101.6,127,152.4 mm时与不同流速的函数关系,其拟合相关系数分别为R2=0.976 12,0.996 33,0.997 09,0.997 24,0.999 1,系数均接近于1,表明拟合关系较为合理,效果较好。

而随着管径从50.8 mm至152.4 mm变化时,在同一流速下,其斯托克斯数(St)也将不断的减小,使得颗粒对弯管的最大冲蚀磨损区域发生在C区域与A区域。对于任一压裂液流速,随着管径的增大,其最大冲蚀速率均呈现减小的趋势。在管径从50.8 mm至152.4 mm变化时,计算得知压裂液流速为5,10,15,20,25 m/s下的弯管最大冲蚀速率分别减小了85.78%,87.53%,89.78%,91.53%,94.01%。在管径为50.8 mm,压裂液流速为25 m/s时,最大冲蚀速率达到了最大值,为0.001 35 kg·m-2·s-1。可以认为随着弯管管径的不断变大,管径的内表面积变大,同等流速的压裂液中固体支撑剂颗粒与管壁发生冲击、碰撞的面积变大,则在单位面积上发生颗粒冲击的次数减少,使得冲蚀磨损速率减小。即得知增大管径,是减小冲蚀磨损的有效途径。
3 结论
1)弯管的冲蚀磨损发生区域共有5处,易冲蚀且严重区域主要有3处,为弯管段靠近出口内壁面的外侧区域(A区域)、弯管段内壁面外侧(液体进入弯管后的正对区域)(B区域)以及直管段靠近弯管段的侧方区域(C区域)。弯管中流场的作用,使得弯管段的流体携带固体颗粒由内侧区域朝着外侧区域运动,而涡流的作用使得部分固体颗粒朝着弯管侧方运动。
2)St<1时,冲蚀磨损主要发生在弯管段靠近出口内壁面的外侧区域(A区域);St>1时,弯管段内壁面外侧(液体进入弯管后的正对区域)(B区域)的冲蚀磨损范围将变大。St增大使得弯管段侧方区域(C区域)的冲蚀磨损程度呈现下降趋势,St=1左右时,侧方区域的冲蚀磨损下降至几乎与出口直管段的冲蚀磨损程度相近,St继续上升,侧方区域的冲蚀磨损情况已趋于稳定。随着St在0~1至St>1变化时,B区域与C区域的冲蚀磨损情况呈现出“此消彼长”的情况。
3)管径越小,其最大冲蚀速率的增长幅度越明显,管径增大,最大冲蚀速率呈减小的趋势,即增大管径是减小冲蚀磨损的有效途径之一。

