以形助数发展学生数学思维力

章佩芳

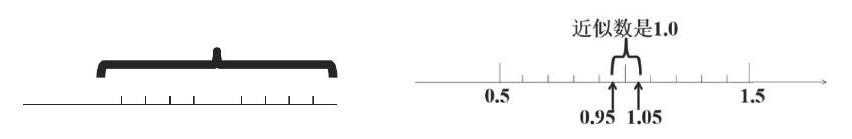
摘 要：《数学课程标准（2011年版）》中的“数形结合”思想，将抽象数学与直观图形有机结合发展学生思维。在抽象数学中发挥直观图形作用，以形助数，能促进学生深入理解知识，形成活动经验，提升抽象思维力。

关键词：以形助数 形象素材

著名数学家华罗庚说过：“数缺形时少直观，形少数时难入微”。意指课标中的“数形结合”。要以形助数，可以借助直观图形化抽象为直观，使抽象的数学知识形象化、复杂的数学问题简明化。

一、以形助数，构建知识模型

学生对数学运算定律的抽象是建立在充分感知基础上的，如在教材资源基础上增加些形象素材，不仅能丰富学生感性认识，还能让学生深刻理解知识，顺利构建模型。^[1]教《乘法分配率》，我创设植树情境让学生解决问题中初步感知乘法分配率，自主举例中验证乘法分配率后通过两个活动促进学生深入理解乘法分配率并抽象其意义：

1.引导学生用不同方法计算长方形的面积并说出这样算的道理。我借助课件出示两个长分别为64、42cm，宽36cm的长方形，然后拼合成一个大长方形，再引导学生用自己的方法计算拼合图形面积，最后动态演示（64+42）×36表示拼合长方形的面积，64×36+42×36分别表示两个原长方形的面积和（拼合长方形的面积）。这样从具体的形出发抽象出数的运算，又回到形解释运算的含义.学生通过对乘法分配律几何意义的理解，也相机促进了对运算算理的理解广度、深度。

2.结合每行5朵红花、3朵蓝花，共4行的花朵图使学生发现了所有例子都能在此图形中找到对应模型，从而促使学生真正理解了乘法分配律，顺利突破了难点，构建起乘法分配律模型。

二、以形助数，探寻知识本源。

“数”的教学中渗透“形”。以形助数，能化现象为本质，帮助学生直观理解数的含义，使隐性道理变得可见易懂，做到既知其然，更知其所以然。如教学《小数的近似数》时，为了让学生理解“为什么保留两位小数要看千分位上数”“为什么要四舍五入”，我结合数轴让学生探究0.984和0.988分别最接近哪一个两位小数，并引导学生说出0.984约等于0.98、0.988约等于0.99的原因，这样从知识本源出发使学生较好理解了“四舍五入”的道理。

然后，我再借助数轴直观演示让学生发现：只要千分位上是4，不管万分位是几，这个数的位置都靠近0.98，故保留两位小数只看千分位上的数。这样触类旁通，使学生深深领悟了保留到哪一位要看下一位数的道理。

近似数1.0和1，哪个更精确呢？这背后的道理也是学生理解的难点。我第三次结合数轴让学生讨论辨析出近似数为1的数在0.5～1.5之间（不包括1.5），近似数为1.0的数在0.95～1.05之间（不包括1.05）。

这样，学生在经历思考讨论与动手操作中理解了两个数虽然相等，但精确度不同，1.0更精确，并提升了问题解决的经验。

三、以形助数，明晰计算算理

我们进行计算教学时，往往关注算法探究，不重视引导学生理解算理，故很多学生只会机械计算。这时，教师以形助数，能让学生直观中理解算理和抽象的算法，并体验直观到抽象的过渡和演变过程，从而达到深入理解算理、切实掌握算法的双向学习目标。^[2]如教《除数是整十数的笔算除法》时，学生独立探究出了92÷30的不同算法，有的把商3写在了个位，有的写在了十位，有的商为30。“3到底应写在什么位置上呢？”这既是学生易错点更是学习的重难点，我让学生根据分小棒过程说竖式中算法。

这样，学生明白了把92根小棒每30根为一份，这样分出了3个30根，也就是90根，还剩2根，所以商3余2，故商应写在个位。此时，以形助数突破了学生的学习难点。紧接着178÷30，我又出示格子图让学生分一分、画一画，启迪学生思维，帮助学生建立起了图形与除法竖式之间的联系，变复杂为简单，使学生掌握算法的同时深悟了算理，计算与思维同步提升。

四、以形助数，把握知识内涵

德国哲学家康德认为：“缺乏概念的直观是空虚的，缺乏直观的概念是盲目的。”由于小学生主形象思维，处于向抽象逻辑思维为主要形式的过渡阶段，以形助数把教材中静止的、难理解的概念以生动形象的直观表象呈现出来，使抽象概念形象化，学生易于理解，也能真正把握概念的实质与内涵。^[3]如教学《速度、时间和路程》，速度概念的理解是教学重点，也是解决相关问题的基础。学生第一次接触速度单位这个复合单位，理解起来有难度。我便创设“学校和图书室相隔400米，小明要走5分钟，小红要走8分钟，谁走得快些？”的情境，学生通过计算发现小明每分钟走80米，比小红每分钟走50米快些。此时，学生对“速度”的理解还停留在较抽象层面上，我便引导学生分别画线段图，把速度概念变成了看得见的数学知识，学生自然形象深刻地理解了。

在小学数学教学中，以形助数是一种降低数学难度的、简便的、高效的教学手段。我们教师要善于利用并挖掘教材资源，结合直观图形进行数学知识的表达，发展学生形象思维的基础上培养抽象思维能力，从而促进学生思维力的飞跃。

參考文献

[1]刘敏.随心潜入“桥”建构细无声——以《乘法分配率》教学为例[J].湖北教育，2016.

[2]罗鸣亮.直面障碍让教学有理有据——《除数是一位数的笔算除法》教学思考[J].小学教学设计（数学），2016.

[3]李冬芳.直观中积累经验无形中涵养素养——例谈借助“几何直观”落实核心素养的培养[J].小学教学研究，2018.