利用整体积分法求解LTI连续时间系统的响应*
陈绍荣,陈柏良,何 健,薛在阳
(1.陆军工程大学通信士官学校,重庆 400035;2.深圳市惟新科技股份有限公司,广州 深圳 518000;3.军委装备发展部军事代表局驻成都地区军事代表室,四川 成都 610041;4.奥特斯科技(重庆)有限公司,重庆 401133)
0 引 言
在时域上求解高阶LTI连续时间因果系统的单位冲激响应h(t)及零状态响应yf(t)时,涉及到处理单位冲激信号δ(t),使得描述高阶LTI连续时间因果系统的微分方程的解模式与高等数学中介绍的解模式有相似之处,但又有明显区别。由于国内外《信号与系统》著作[1-2]借助物理概念,给出了高阶LTI连续时间因果系统单位冲激响应δ(t)及零状态响应yf(t)的解模式,因此,缺乏严谨的推导过程。针对连续时间反因果信号和连续时间因果信号的积分运算问题,基于著作[3]的分段积分法和分部积分法,本文提出了整体积分法。基于整体积分法,提出了高阶LTI连续时间因果系统时域分析的不定积分降阶法和上限积分降阶法,分析结果表明,LTI连续时间因果系统的单位冲激响应为因果信号,在因果信号作用下其零状态响应为因果信号。圆满地解决了高阶LTI连续时间因果系统零输入响应、零状态响应及全响应的时域求解问题。
1 截断信号的积分
若连续时间信号x(t)定义在整个时间区间,则称x(t)为无时限连续时间信号。一个无时限连续时间信号x(t)可以分解成连续时间反因果信号与连续时间因果信号之和,即:
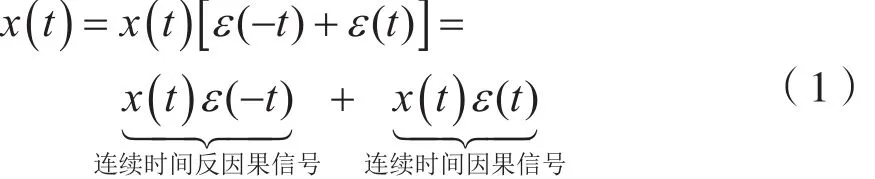
式中,ε(t)为单位阶跃函数。
实际工作中,信号发生器的输出是连续时间因果信号。因此,在LTI连续时间因果系统的时域分析中,经常涉及连续时间因果信号的积分问题,即截断信号的积分问题。
例 1:已知连续时间因果指数信号 f(t)=eλtε(t),其中,λ为常数,ε(t)为单位阶跃函数,试求积分运
解:方法1:采用分段积分法。
(1)当t<0时,考虑到f(t)=eλtε(t),若 -∞≤τ≤t<0,则有 ε(t)=0,于是:
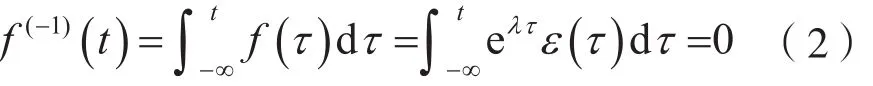
(2)当 t>0 时,考虑到 f(t)=eλtε(t),则有:
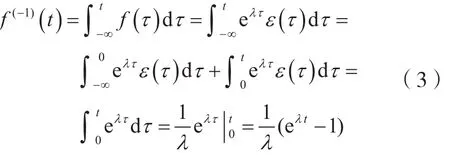
综合式(2)及式(3),可得:
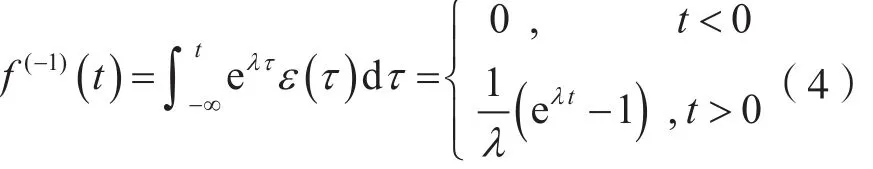
式(4)表明,利用分段积分法,对连续时间因果指数信号做积分运算,其结果是一个分段函数。
方法2:采用分部积分法。
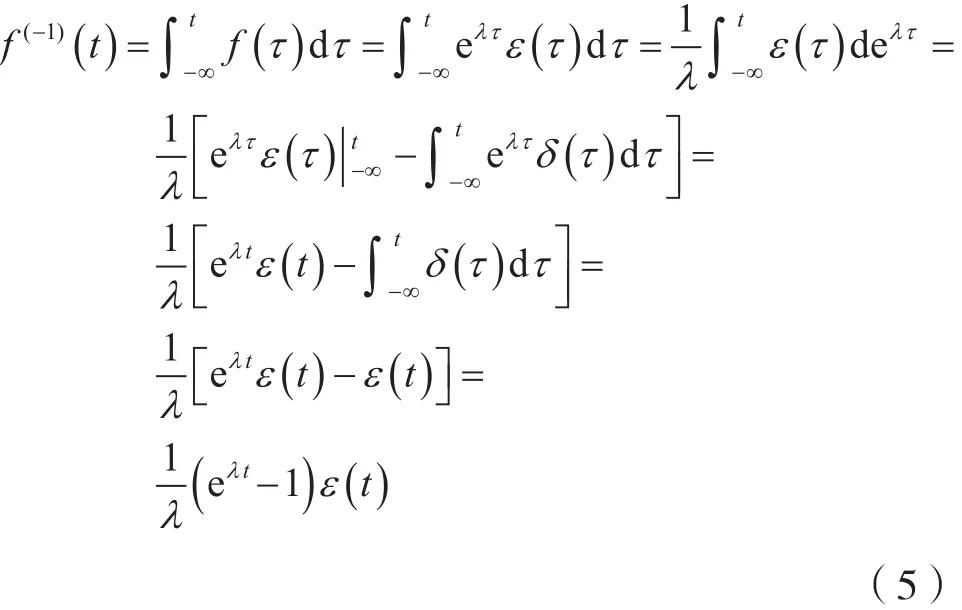
式(5)表明,利用分部积分法,对连续时间因果指数信号做积分运算,其结果虽然表示成了一个连续时间因果信号,但是积分运算的过程十分冗长。
方法3:采用整体积分法。
若将连续时间反因果信号或连续时间因果信号的表达式视为一个整体,找出其原函数,则可直接利用牛顿—莱布尼茨公式解决问题。这种求解连续时间反因果信号或连续时间因果积分运算的方法,称为整体积分法。
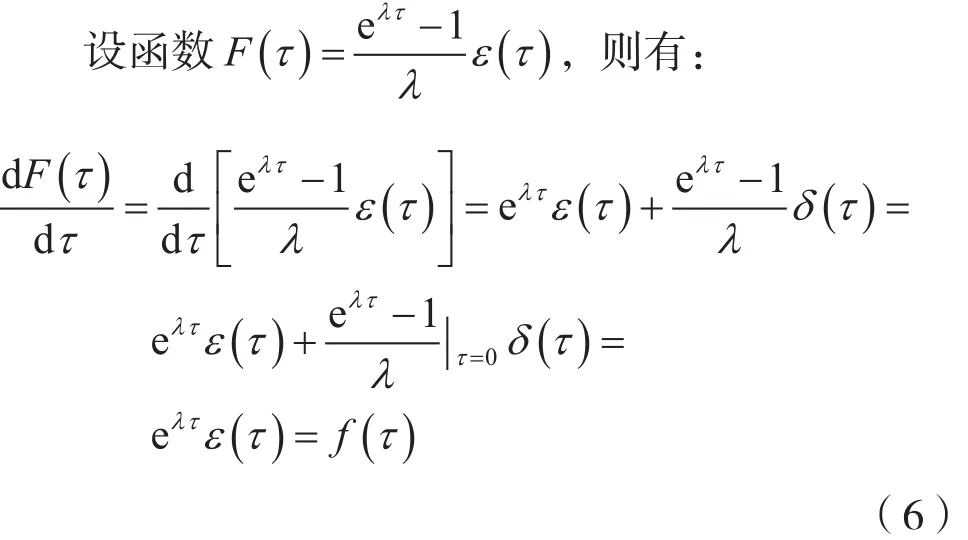
式(6)表明,所设函数F(τ)是所给因果指数函数f(τ)的一个原函数。
于是,由牛顿—莱布尼茨公式可得:
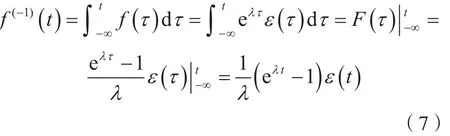
结论1:
对连续时间因果信号做积分运算,采用整体积分法不仅是一种最简便的方法,而且其结果自动表示为因果信号。
2 构建基于整体积分法的连续时间反因果信号和因果信号的不定积分公式
考虑到 ε´(t)=δ(t),则有:

对式(6)两边做不定积分,可得:
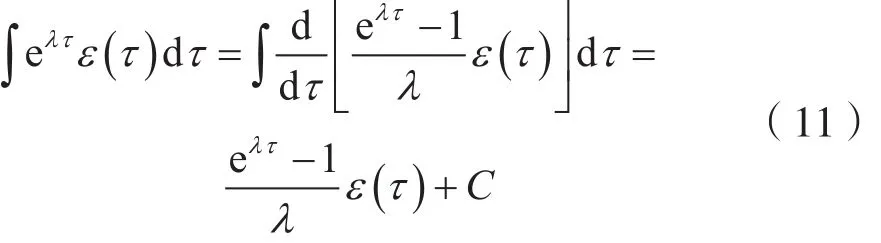
式中,C为任意常数。
由式(11)可得:
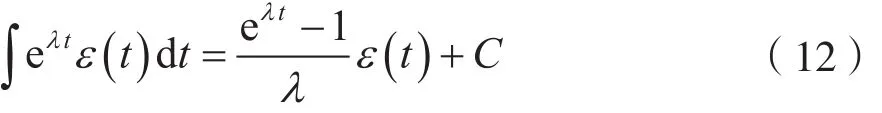
式中,C为任意常数。
在式(12)中,令 λ=a+jω0,C=C1+jC2,则有:
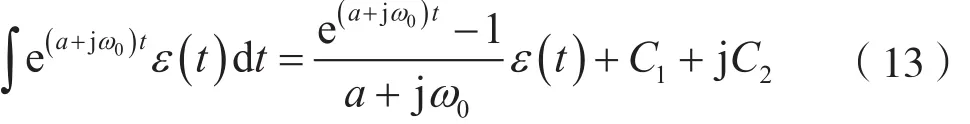
考虑到欧拉公式,由式(13)可得:

考虑到式(14)中的实部和虚部分别相等,则有:
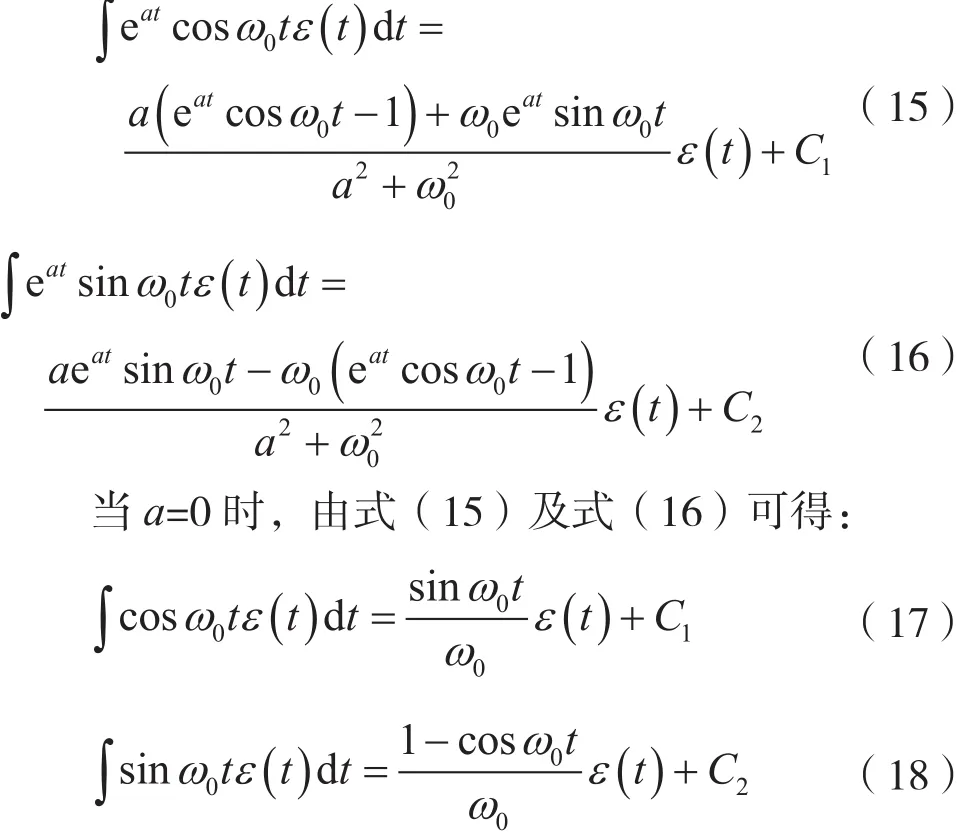
考虑到式(12),则有:
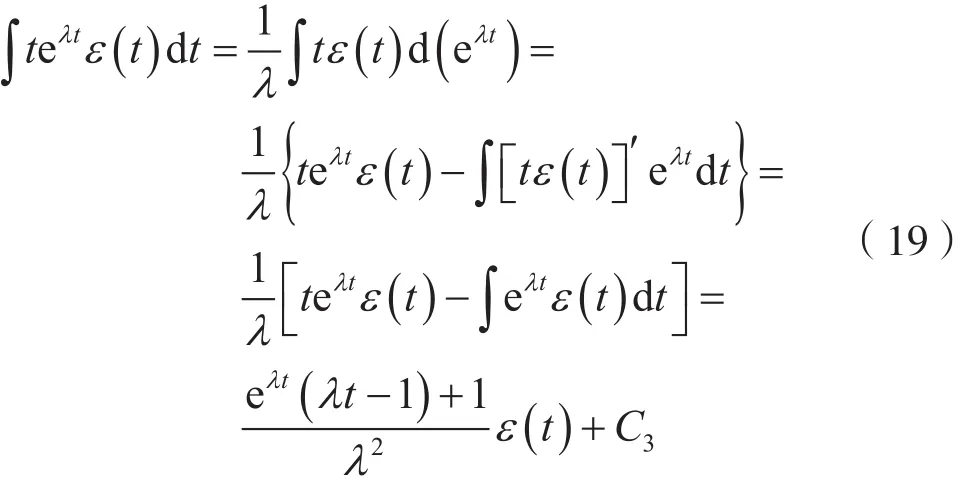
为了便于运算,表1列出了常用的连续时间因果信号和反因果信号的不定积分公式,其中,C为常数,λ是λ≠0的实数或复数。
3 LTI连续时间因果系统输出与输入的时域关系
设描述二阶LTI连续时间系统响应y(t)与激励f(t)关系的微分方程为:
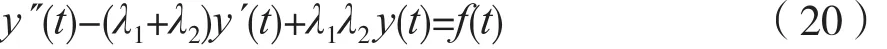
式中,λi<0(i=1,2)。假设系统的起始状态 y´(-∞)=y(-∞)=0。
显然,微分方程式(20)可写成:
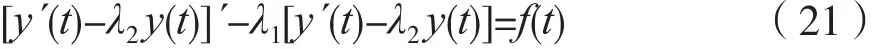
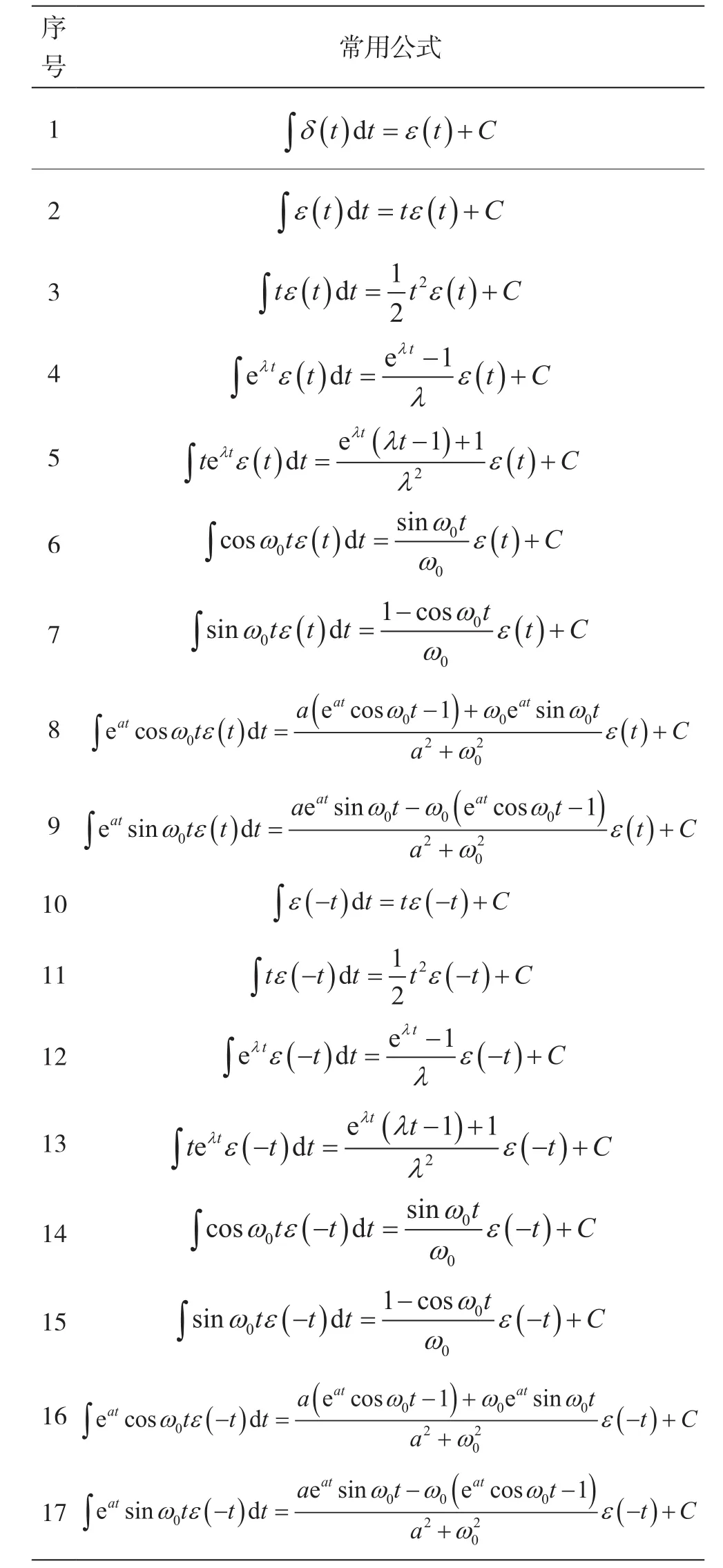
表1 常用连续时间因果信号和反因果信号的不定积分公式
设:

则有:
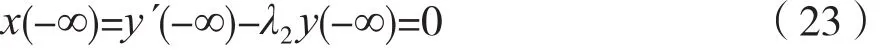
并且,微分方程式(21)可写成一阶微分方程,即:
将一阶微分方程式(24)两边乘以e-λ1t,可得:
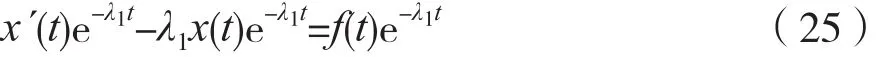
利用乘积求导法则,对式(25)的左边做逆向改写,可得:

由式(26)可得:
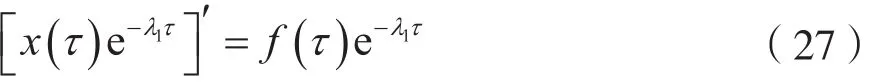
在τ∈(-∞,t]上,对式(27)两边做上限积分运算(累加),可得:

考虑到式(23),由式(28)可得:
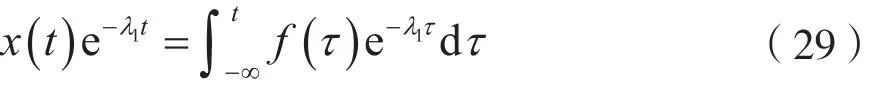
由式(29)可得:
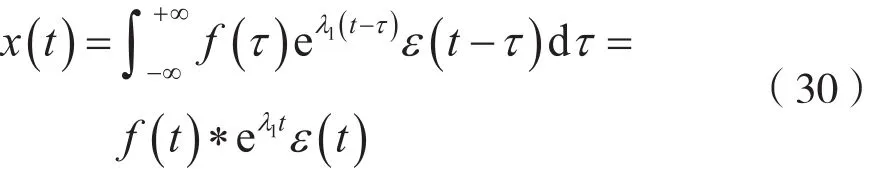
对比微分方程式(22)及微分方程式(24),并注意到式(30),则微分方程式(22)的解y(t),即二阶LTI连续时间系统的零状态响应yf(t)可以表示为:
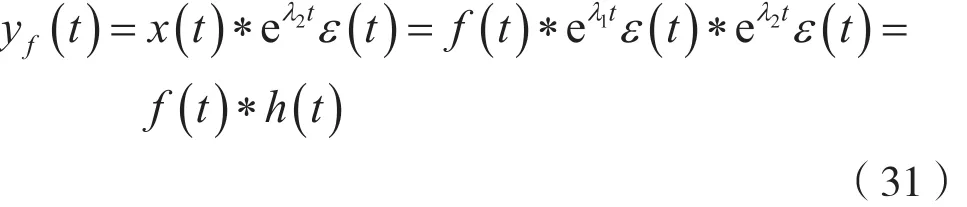
式中,h(t)为二阶LTI连续时间因果系统的单位冲激响应,并且 h(t)=eλ1tε(t)*eλ2tε(t)。
上述这种导出二阶LTI连续时间因果系统输出与输入关系的方法,称为上限积分降阶法。
式(31)揭示了LTI连续时间因果系统的零状态响应可以用激励和系统单位冲激响应的线性卷积进行计算。
4 LTI连续时间因果系统的时域分析
下面以举例的方式,介绍利用整体积分法来求解高阶LTI连续时间因果系统的响应。
例2:设描述二阶LTI连续时间因果系统响应y(t)与激励f(t)关系的微分方程为:

若系统的激励为f(t)=15e-2|t|,系统的起始状态y´(-∞)=y(-∞)=0。
(1)试求系统的单位冲激响应h(t)。
(2)试求t≥-∞时系统的零状态响应yf(t)。
(3)若t<0时的激励用于给系统建立初始状态,试求t≥时系统的零输入响应yx(t)、零状态响应yf(t)及全响应y(t)。
解:(1)考虑到微分方程式(32),则有:
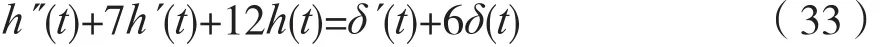
对微分方程式(33)的左边改写,可得:

将式(34)两边乘以e3t,可得:
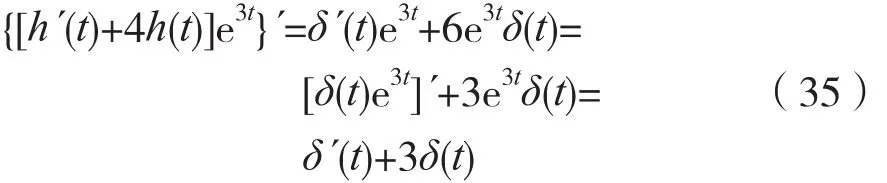
对式(35)两边做不定积分运算,并注意到表1中序号为1的不定积分公式,可得:
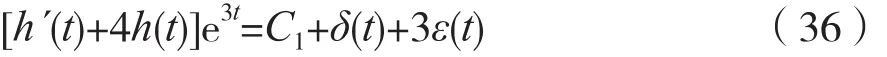
由式(36)可得:
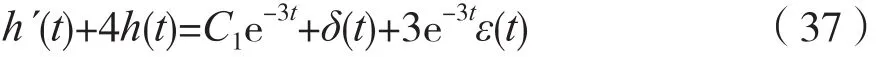
同理,将微分方程式(37)两边乘以e4t,可得:
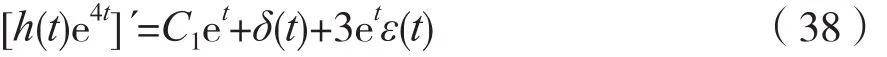
对式(38)两边做不定积分运算,并注意到表1中序号为1和4的不定积分公式,可得:

由式(39)可得:
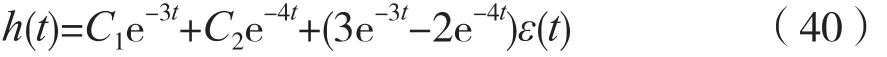
考虑到系统的初始状态h´(0_)=h(0_)=0,由式(40)可知,C1=C2=0,于是所求二阶LTI连续时间因果系统的单位冲激响应为:

上述这种求解LTI连续时间因果系统的单位冲激响应的方法,称为不定积分降阶法。
结论2:
式(41)揭示了LTI连续时间因果系统的单位冲激响应h(t)是一个连续时间因果信号。
(2)考虑到:
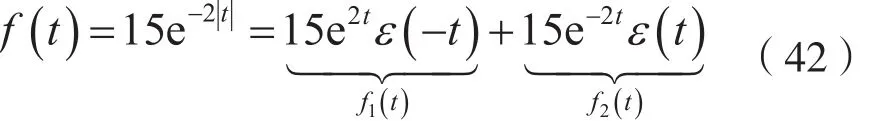
由式(31),并注意到式(42)及表1中序号为4和12的不定积分公式,可得:

(3)由式(43)可知,当t≥0时,系统的零输入响应为:
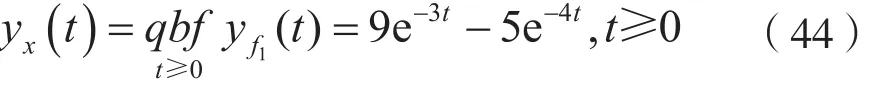
系统的零状态响应yf(t)为:

系统的全响应y(t)为:
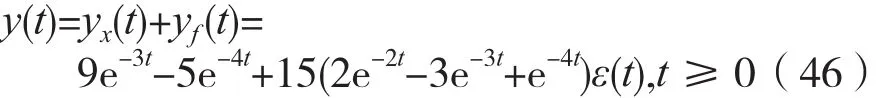
5 结 语
本文提出了整体积分法,解决了连续时间反因果信号和连续时间因果信号积分过程冗长的问题。基于整体积分法,提出了高阶LTI连续时间因果系统时域分析的不定积分降阶法、上限积分降阶法。揭示了LTI连续时间因果系统的单位冲激响应为因果信号,在因果信号作用下其零状态响应为因果信号。圆满地解决了高阶LTI连续时间因果系统零输入响应、零状态响应及全响应的时域求解问题。

