基于层次分析法构建工程制图基础教学目标指标体系与权重计算

邹腾安 邓静子 张湘 徐海军 常雨康

摘要：工程制图基础是国防科技大学历史悠久、覆盖面广、影响力大、建设水平高的公共基础课。文章首先分析了该课程的课程定位，进而介绍了层次分析法，然后基于层次分析法构建了该课程培养目标的指标体系，并且计算了各级指标的相对权重和综合权重，最后对方案层各指标的综合权重进行了归纳分析，通过层次分析法计算得到的方案层各指标的综合权重分布墓本符合该课程的教学目标的基本设定，研究结果可以用于指导该课程教学内容与考核体系的具体设置。

关键词：教学目标;层次分析法;指标体系;相对权重;综合权重

中图分类号：G642 文献标识码：A 收稿日期：2019-07-23 文章编号：1674-120X（2019）29-0123-02

一、课程定位分析

要想得到一件机械产品，设计者首先要有产品的设计和构思，然后绘制工程图样，交给工人师傅进行零件的加工和装配，最后得到这件产品。整个研发与设计流程并没有结束，设计者还要根据工程图样里面的尺寸、公差等技术信息，对产品进行检验，校核产品是否符合其设计要求。可以看出，工程图样在整个产品研制过程中起到核心的作用。工程图样是表达产品信息最好的方式，被誉为工程界的技术语言，是技术部门重要的技术文件。工程制图就是研究绘制和阅读工程图样原理和方法的学科Q

工程制图基础课程不仅培养空间想象和形象思维能力，还培养仪器绘图、徒手绘图、计算机绘图技能，使学员能够阅读和绘制一定复杂程度的工程图样，了解相关国家标准，养成认真负责的工作态度和严谨细致的工作作风。

二、层次分析法介绍

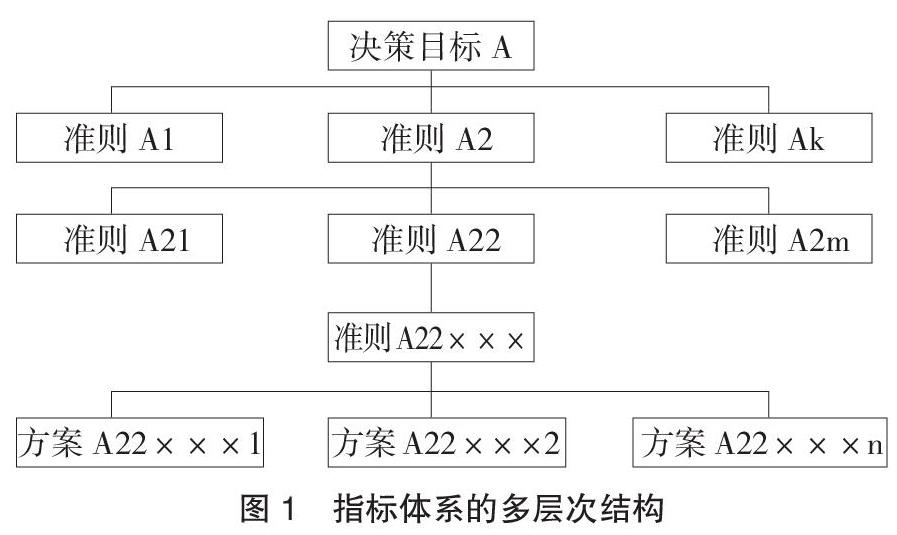
层次分析法（AHP）是美国匹兹堡大学T.L.Saaty教授在20世纪70年代中期提出的一种多目标、多准则的复杂大系统分析方法。这个方法一般应用于建立多层级的指标体系，并且需要确定指标体系中各指标（准则）相对于其上一层指标和总指标的相对重要性（或称为权重）。AHP法的系统分析，是把指标体系所包含的要素分成了不同的层级，按照最高层（目标层）、若干有关的中间层（准则层）和最末层（方案层）的形式排列，形成了指标体系的多层次结构，如图1所示。

三、教学目标的指标体系

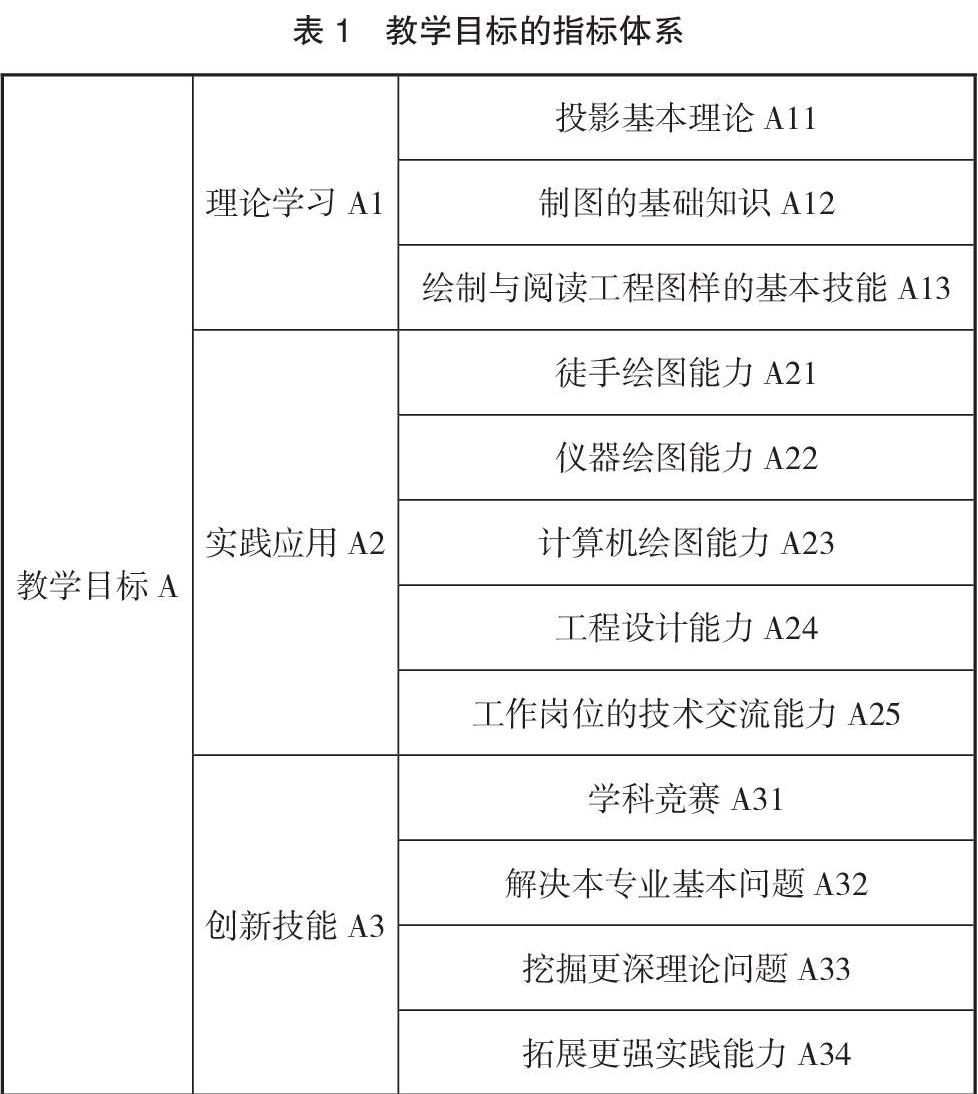
基于上文的分析，综合专家意见，基于层次分析法建立教学目标的指标体系。工程制图基础课程的教学目标A，属于目标层指标;教学目标A向下一层级进行分解，可以分解为理论学习A1、实践应用A2和创新技能A3等3个准则层的指标;理论学习A1再向下一层级进行分解，可以分解为投影基本理论A11、制图的基础知识A12、绘制与阅读工程图样的基本技能A13共3个方案层的指标;实践应用A2再向下一层级进行分解，可以分解为徒手绘图能力A21，仪器绘图能力A22、计算机绘图能力A23、工程设计能力A24、工作岗位的技术交流能力A25共5个方案层的指标;创新技能A3再向下一层级进行分解，可以分解为学科竞赛A31、解决本专业基本问题A32、挖掘更深理论问题A33、拓展更强实践能力A34共4个方案层的指标。整理教学目标A的指标体系，可以建立工程制图基础课程教学目标的指标体系，如表1所示。

四、基于层次分析法确定指标权，

在一般情况下，指标权重是凭个人经验给出，但是凭经验给出的权重带有较大的主观性，有时不能客观地反映实际情况，评价结果可能“失真”。为了获得较为客观并且合理的权重，本文将采用层次分析法对相关评价指标权重进行基本界定。

运用层次分析法确定指标权重值，大体需要经过以下三个步骤：

步骤I，组织专家完成基于层次分析法设计的关于指标权重确定的相关问卷，通过对同一层次中各指标的重要性进行“两两比较”，在确定该组指标相对重要性的基础上，构造出权重判断矩阵，

步骤2，根据判断矩阵计算出来本层次各指标的相对权重，并且检验判断矩阵的一致性，从而进行层次内的指标排序。

步驟3，计算出单个指标在整个指标体系中的综合权重数值（绝对权重），从而进行指标体系的总排序。

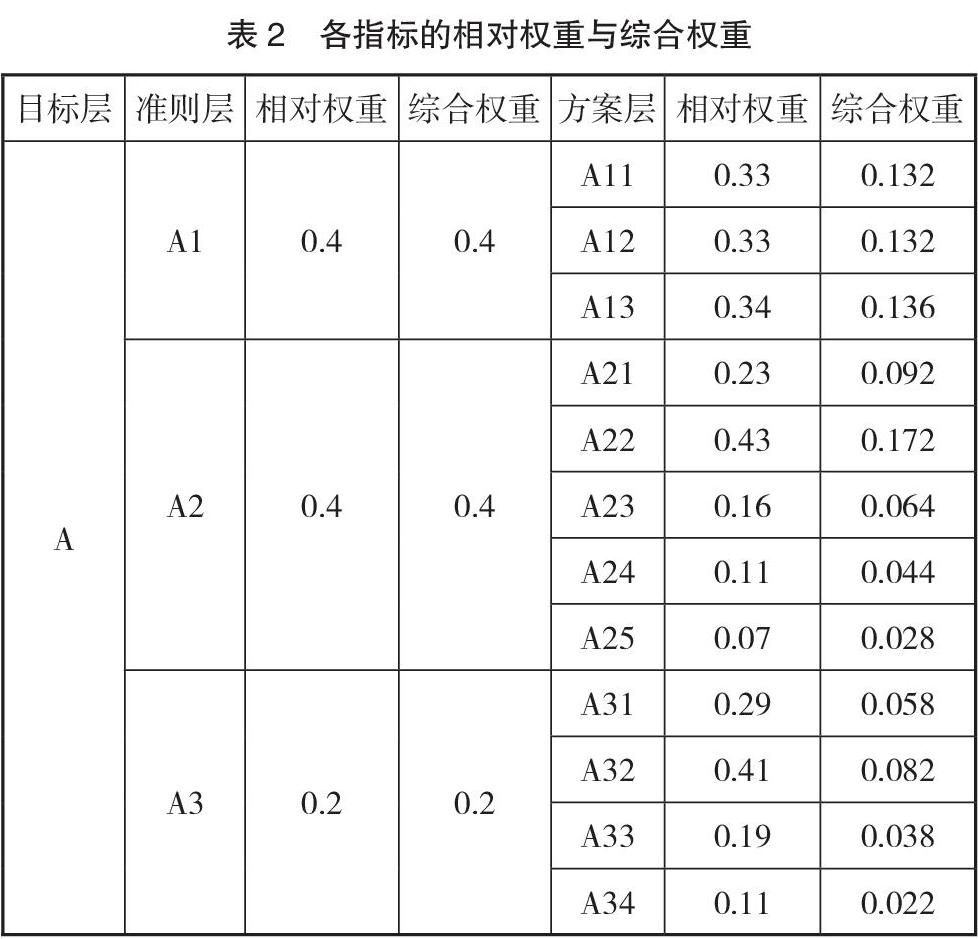
基于上述方法与计算步骤，本文基于层次分析法计算了教学目标指标体系中各层级指标的相对权重与综合权重，计算结果如表2所示。

基于表2中的计算数值，将方案层中的A11、A12、A13、A21、A22、A23、A24， A2s、A31、A32、A33、A34等指标的综合权重进行统日分析，生成方案层各指标综合权重数值的分布，如图2所示。

从图2可以看出，仪器绘图能力A22的综合权重数值最高，绘制与阅读工程图样的基本技能A13次之，其他指标的权重更次。此计算结果基本钧二合本课程的教学目标定位，即通过本课程学习，首要的是锻炼学员的仪器绘图能力，次要的是使学员掌握绘制与阅读工程图样的基本技能，同时兼顾投影基本理论与制图的基础知识的学习，进而掌握徒手绘图能力、解决本专业基本问题等其他学习目标。

五、结语

本文分析了工程制图基础的课程定位，介绍了层次分析法ARP，并且基于AHP法构建了教学目标的指标体系，介绍了基于ARP法确定各层级指标权重数值的具体步骤，进而确定了教学目标指标体系中各层级指标的相对权重与综合权重数值，最后对指标体系方案层中各指标的综合权重进行了归纳整理与分析。可以看出，仪器绘图能力的综合权重数值最高，绘制与阅读工程图样的基本技能次之，其他指标的权重更次。此计算结果基本符合本课程的教学目标设定，本文的研究结果可以用于指导本课程教学内容与考核体系等的具体设置。

参考文献：

[1]L.A.Zadeh.Fuzzy sets[J].Information and Control，1965（8）：338-353.

[2]R Lowen.Mathematics and fuzziness，Part I[J].FuzzySets and Systems，1988， 27（1）：1-3.

[3]R Lowen.Mathematics and fuzziness，Part 11 [J].FuzzySets and Systems，1989，30（1）：1-3.

[4]梁保松，曹殿立.模糊数学及其应用[M].北京：科学出版社，2007.

[5]谢季坚，刘承平.模糊数学方法及其应用（第四版）[M].武汉：华中科技大学出版社，2017.

[6]赵黎明，史慧.高校人才培养模式的实证研究[J].天津大学学报（社会科学版），2015，17（3）：204-209.

[7]王涛.模糊综合评判在高校排课系统评价中的应用[J].大学数学，2006，22（2）：5-10.

基金项目：湖南省哲学社会科学基金项目（16YB0008）;湖南省普通高等学校教学改革研究项目（湘教通[2016]400号-序号19号）。

作者简介：邹腾安（1984-），男，山东泰安人，讲师，博士研究生，研究方向：机械设计与理论、新概念发动机、智能无人系统、高等教育。