例谈初中数学试题的变式改编与创新

林文展

【摘要】近年来，伴随新课改渐渐深入，各地中考数学科目试卷出现了很多带有时代气息、推陈出新并且有着锐意进取的好试题。同时这些试题设计巧妙、构思精细、构造新颖，着实令人佩服。实际上，这些新颖试题并非命题人凭空想出来的，而是命题人在经典例题以及练习题基础之上进行变式改编以及创新得到的。所以，主要对初中阶段数学试题的创新以及变式改编进行探究，以期给实际教学提供相应帮助。

【关键词】初中数学 数学试题 变式改编 创新

纵观最近几年各地的中考数学科学试题，其注重对考生实践能力以及创新思维的综合考查，而且试题多以探究形式提供相应的阅读资料，以此来让考生借助所学知识进行解题，并且引导学生进行相应的思考。这些试题非常新颖，重视引发学生进行深层思考。假设数学教师试着将此类问题的延伸引入到平时教学中，让初中生亲身经历思考以及收获的过程，这样可以有效提高教学效果。

例如，如图1所示，在直角三角形中，AC=BC，∠ACB是直角，且点P是AB中点。（1）请分别写出P点到△ABC三个顶点的距离关系，同时说明理由。（2）如果M点和N点分别是AC以及BC边上的动点，而且在运动期间始终保持BN=CM，请对△PMN形状进行判断，同时对结论进行证明。

变式一：把原命题当中问题（2）变成：如果M点和N点分别是AC以及BC边上的动点，同时在运动期间∠MPN始终为直角，试猜想PN和PM、BN和CM间的关系，同时对结论加以证明。

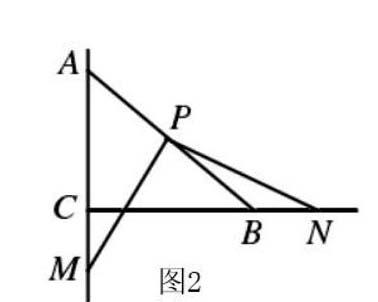
变式二：把原命题当中问题（2）变成：如图2所示，如果M点和N点分别在AC以及BC边的延长线上进行运动，同时在运动期间∠MPN始终为直角，试猜想PN和PM、BN和CM间的关系，同时对结论加以证明。

变式三：把原命题可以变成相应的操作题，具体如图3所示，在△ABC当中包含一个45°的三角板，而△PDE当中含有30°的三角板，同时P点为AB边中点，现将△PDE围绕P点进行旋转角θ，其中0<θ<45°，同时PD和AC相交于点M，BC与PE相交于点N，试猜想PN和PM、BN和CM间的关系，同时对结论加以证明。

变式四：如果把变式三当中的“P点为AB边中点”改变成“BP∶AP=3∶1”，其他条件不变，试猜想PN和PM、BN和CM间的关系，同时对结论加以证明。

实际上，不少中考题的类型与上述变式习题的类型十分相似。

如图4所示，在等腰直角三角尺FEG的直角边和正方形ABCD当中两条边重合，如果正方形ABCD一直保持不动，把三角尺FEG围绕着斜边EF中点O按着顺时针的方向进行旋转，会得到以下图形。

如图5所示，当AB和EF相交于M点，BD和FG相交于N点之时，经过对FN和BM长度进行观察以及测量，试猜想FN和BM间的关系，同时对结论加以证明。

从以上变式问题当中能够看出，数学教师可以教材例题以及练習题为基础进行变式习题的设计，同时以此来引导学生思维进行纵深发展，激发学生求知欲望，并且对其想象、观察以及转化能力加以培养。所以，在日常教学期间，数学教师应当加强对基础问题的变式改编以及创新。

综上可知，最近几年的中考数学当中出现很多创新类的试题，其并非无源之水。究其根源，这些试题都是在教材例题以及练习题的基础上通过不同变式得到的。所以教学期间，教师应当引导学生对习题变式间具有的内在联系进行深入了解，并且对中考真题、练习题以及例题对应的变式方法加以掌握，同时通过对变式规律加以探究，进行改造、整合、变式以及创新训练，这样可以跳出题海，实现触类旁通，举一反三，进而达到事半功倍的效果。

参考文献：

[1]徐枫.浅谈数学变式教学在初中数学教学中的应用[J].名师在线，2018，（29）：60.

[2]白雪峰.提炼基本活动经验 感悟数学理性之美——以一道初中数学竞赛试题的多种解答与变式拓展为例[J].数学通报，2018，（02）：28.

[3]张宁.一道初中数学竞赛试题的多种解法[J].数理化学习，2017，（05）：38.