变截面杆交界面处应力均匀性问题计算机仿真

齐敏菊，高光发

(1. 淮南师范学院计算机学院，安徽 淮南 232001；2. 南京理工大学机械工程学院，江苏 南京 210094)

为了利用一维弹性波理论分析变截面杆中应力波在交界面上的透反射现象，假设两杆虽然截面积不相等，但皆两杆的界面远小于其长度，因而可以不考虑变截面处附近相对较长一段区域内分应力状态[1-2]。然而，在实际应用中，这一条件不一定完全得到满足，如在分离式Hopkinson压杆试验过程中，试件的长度一般皆小于其直径，此时分析交界面两端区域的应力场分布不均匀性就不得不考虑了。对于截面突变对应力波传播的研究由于应力波理论的非线性，利用理论给出准确的三维解析解较难，大多为定性的结论。同时利用广义波阻抗理论所给出的结果在一定程度上能够满足当前应用需求，然而，随着科研的深入，对科研定量结果的精度要求日益变高，不少学者利用数值仿真方法对变截面杆中应力波弥散问题开展研究[3-8]，由于当时数值仿真手段和计算机硬件的限制，这些研究大多侧重于二维仿真研究，但也给出了相对准确科学的结论。本文在此前提下，利用ABAQUS非线性动力学软件，在量纲分析的基础上，研究影响变截面杆两侧应变场分布的因素及其影响规律，对分析应力波在变截面杆中的传播演化机制和精细化分离式Hopkinson压杆试验的设计与数据处理有着一定的定量参考价值。

1 仿真模型与量纲分析

如图1所示，假设杆长度无限，细长杆截面积分别为A1和A2，两杆材料相同，其密度和声速分别为ρ和C，设杆材料为弹性材料，不考虑其屈服强度；入射波为单脉冲压缩加载波，其强度为P。

图1 变截面杆简化模型

由此可以知道交界面两侧紊乱区长度(自交界面起计算)虽不一定相等，但理论上皆可以写为

L=f(ρ，C，P，A1，A2)

(1)

利用量纲分析理论即可得到

(2)

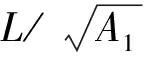
此问题为典型的轴对称问题(见图1)，利用ABAQUS软件建立此仿真模型，其中大杆长度为500mm，截面直径为10mm，小杆长度为250mm，其截面直径分别为9mm、8mm、7mm、6mm、5mm、4mm、3mm、2mm和1mm，即面积匹配系数分别为0.81、0.64、0.49、0.36、0.25、0.16、0.09、0.04和0.01；杆材料密度为7.8mg/mm3，杨氏模量为210GPa，可以计算出杆材料声速为5 189mm/ms。仿真模型为二维轴对称模型，取二分之一模型为研究对象，网格尺寸为0.1mm×0.1mm。矩形脉冲波峰值应力分别为100MPa、200MPa、300MPa、400MPa和500MPa。

根据波动理论，容易计算出不同面积匹配系数时的无量纲反射波和透射波强度

(3)

取杆中远离变截面区域的两个截面，可以得到杆中准一维波稳定传播阶段的反射波和透射波强度，数值仿真结果与理论结果对比如图1所示。

图2 不同截面积匹配系数下数值仿真与理论结果对比

从图2可以看出，数值仿真结果与理论结构基本一致，说明了该数值仿真模型的科学与准确性。

2 应力紊乱区的特征分析

以面积匹配系数为D=0.01为例，从仿真结果可以看出，如图2所示，应力波到达变截面处发射和透射波在附近区域呈现紊乱状态，而且由于两杆的直径不同，其紊乱区间的长度不同，容易看出，小直径部分紊乱区间较小，而大直径部分紊乱区间较大。呈现此现象主要原因是因为原本入射大直径杆中应力是均匀的且剪应力存在，当应力到达交界处时，由于中间区域与小直径杆直接接触，而外部区域交界面则为自由面，其应力波反射应变场的不均匀导致其应力场的紊乱，沿着径向方向存在剪应力，如图3所示，图3中取面积匹配系数为0.25时交界面处大直径杆一侧单元上的剪切应力参数，为对比不同入射强度时该界面上的剪切应力，定义纵坐标为无量纲剪切应力

(4)

式中：σ12表示单元上的剪切强度。

图2 应力波到达“交界面”处透反射波的紊乱现象

图3 不同入射强度剪切应力沿径向方向上的分布

从图3中可以看出，不同入射强度时交界面处大口径杆上的剪切应力沿径向坐标的变化而变化的趋势和无量纲数值基本相同；当径向坐标为0时，即中心点上单元所受剪切应力接近于0，随着径向坐标逐渐增大，即逐渐从对称轴中心线向外时，单元上的剪切应力逐渐增大，直到到达小杆最外侧对应的大杆接触点处达到最大，此时剪切应力均达到接近入射压缩强度值；坐标继续增大式，此时单元即为大杆自由端面上的单元，其剪切应力急剧减小至0。

对于不同面积匹配系数而言，当入射强度相同时，其剪切应力的径向分布特征类似，如定义两杆交界面上大杆侧单元的径向坐标与小杆半径之比为无量纲径向坐标，可以得到图4。从图中可以看出随着面积不匹配系数的增大，即截面积逐渐接近，杆中心周围的剪应力越小，其意味着压应力越均匀。同样，也可以得到从交界面起沿着两杆中心轴线方向上其正应力的分布图，如图5～图6所示。

图4 不同面积匹配系数剪切应力沿径向方向上的分布

图5 小杆中正应力沿轴线方向上的不均匀分布

从图5和图6中可以看出：在小杆中，从两杆交界面向小杆方向沿轴线坐标增大时，其轴向正应力逐渐增大，直到应力达到均匀区；在大杆中，从两杆交界面向大杆方向验证轴线坐标增大时，其轴向正应力逐渐减小，直到达到均匀区。

3 应力紊乱区的长度及其影响因素

从图5和图6也可以看出，当面积匹配系数小时沿着两杆中心轴线方向上的应力梯度大，而随着面积匹配系数的增大，其应力梯度逐渐减小，其意味着随着面积匹配系数增大，应力均匀性越好。如果我们定义一个应力不均匀度

(5)

式中：σ22表示杆中心轴向正应力，σuni表示均匀区杆中心轴向正应力；从定义可以看出，应力不均匀度越低杆中应力越均匀，等于零时完全均匀。我们可以计算出不同面积匹配系数时小杆中的最大应力不均匀度，如图7所示。从图7中可以看出，随着面积匹配系数的增大，小杆中最大应力不均匀度逐渐呈二次函数从26.2%减小到8.2%；对于大杆而言，最大应力不均匀度从694.1%降低到112.2%。

图6 大杆中正应力沿轴线方向上的不均匀分布

图7 杆中不均匀度与面积匹配系数之间的关系

假设当|(σ22-σuni)/P|×100%<1%时认为杆中应力达到均匀，否则就处于应力紊乱区，并定义一个无量纲应力紊乱区长度为

(6)

可以从仿真结果中得到当入射强度为100MPa时，在不同面积匹配系数条件下两杆中的应力紊乱区长度，如图8所示。从图中可以看出，随着面积匹配系数的提高，两杆中的应力紊乱区无量纲长度均有下降的趋势，而且大杆中更为明显：小杆中当面积匹配系数为0.09时，其最大应力紊乱区无量纲长度为0.60，面积匹配系数达到0.81时，其最大应力紊乱区无量纲长度降为0.51，降幅达到15%；而大杆中面积匹配系数为0.09时，其最大应力紊乱区无量纲长度为1.00，面积匹配系数达到0.81时，其最大应力紊乱区无量纲长度降为0.7，降幅为30%。

图8 杆中应力紊乱区无量纲长度

图9 入射强度对杆中中心轴向上应力分布的影响

当入射强度从100MPa上升到200MPa、300MPa和400MPa时，计算结果显示以上规律基本一致，而且在杆中心轴线上，其无量纲正应力(正应力与入射强度之比)与入射强度为100MPa时基本一致，因此，可以认为在弹性阶段，对于同一种杆材料而言，入射波强度对于杆中紊乱区长度影响可以不予考虑，影响两杆中应力紊乱区应力分布和应力紊乱区无量纲长度的只有面积匹配系数。

4 结论

在材料的分离式Hopkinson杆动态力学性能试验过程中，两个基本假设之一即是认为应力波在杆和试件中均匀的以平面波的形式传播，然而，在实际过程中，由于试件和杆截面的不匹配会导致在两杆与试件的接触面附近产生应力紊乱，了解并定量确定紊乱区的应力不均匀程度和长度对于确定试件的径向与轴线尺寸以及提高试验的准确性具有重要的指导意义。以此为背景，开展系列仿真研究，并得到了以下主要结论。

首先，分析表明，影响应力紊乱区应力分布情况和长度最重要的两个因素即为无量纲入射波强度和面积匹配系数，而数值仿真显示，无量纲入射波强度对于应力紊乱并没有明显的影响；因此，影响应力紊乱区应力不均匀度和长度的主要是面积匹配系数。

其次，产生应力紊乱区的主要原因是由于界面两端由于面积不匹配导致在大杆侧单元产生存在应力梯度的剪切应力；随着面积匹配系数的增加，两杆中应力不均匀度皆逐渐降低；同时，两杆中紊乱区无量纲长度也随之逐渐降低，但在绝对尺寸上，当大杆直径不变时，随着小杆直径的减小，小杆中应力紊乱长度却也随之减小。

第三，当面积匹配系数为0.09～0.81区间内的值时，应力紊乱区长度在大杆和小杆中的相对尺寸基本分别在0.70～1.00和0.51～0.60之间，因此，考虑到大杆的尺寸与应力波测量方式，对于大杆中应力波测量并没有影响，而试件一般长径比皆约为0.5作用，因此面积匹配系数对试件中的应力不均匀分布有着明显的影响。