Dynamic Response of Shipbuilding Sandwich Plate System Subjected to Impulsive Loading
ZHAO N , YE Ren-chun, TIAN A-li , CUI Jie , REN Peng, WANG Ge
(a. School of Science; b. School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China)
Abstract: Sandwich plates with flexible core are generally designed to bear dynamic or impact loads due to their good shock resistance among many other advantages. This paper presents a new higherorder theoretical model for describing the dynamic response of sandwich plates with a flexible core.The governing equation is first established from the equilibrium differential equations of the structure that is simply supported along all its boundaries. The pulse load is simplified as a sinusoidal function. Once the governing equation is solved, it is applied to some example sandwich structures.In addition, a series of parametric studies are carried out to investigate the influences of some key design parameters, including skins/core thickness ratio, skins/core Young’s modulus ratio of sandwich plate, etc. Expectedly, the newly developed theoretical solutions and parametric studies provide some insights into the dynamics responses, which may be helpful for the sandwich structures to be used in the shipbuilding industry.
Key words: sandwich plate; flexible core; higher-order theory; impulse load;dynamic response
0 Introduction
During the recent past decades, lightweight sandwich plates, which are generally composed of two stiff face sheets and a flexible core, emerged as important structural/functional elements in technological fields such as naval, automotive, and mechanical and civil engineering[1]. The mechanical properties of composite structures should be investigated carefully for the spread and application of composite structures in long-span lightweight structures[2-3]. Sandwich plate with flexible core is generally designed to bear dynamic loads and impact loads in naval architecture and ocean engineering due to the flexible core of sandwich plate with good shock resistance. General impact loads include sudden applied load, sinusoidal pulse load, rectangular pulse load, triangular pulse load, periodic wave loads and so on. When steel/polyurethane sandwich plates are used in naval architecture and ocean engineering, they are often subjected to dynamic impact loads due to the complexity of the environment, and the probability of high-strength impact loads such as high-speed collision and explosion during service is higher.
The skins of sandwich plates are typically thin and bear longitudinal and bending loads.As the core is comparatively thick and is generally composed of a relatively soft material, the deformation behaviour of the sandwich is different from the corresponding behaviour of laminated plates and monolayer plates[4]. To account for the specific deformation behaviour, a large number of specific plate and shell models for sandwich/laminate plates have been developed.Sandwich plates with flexible cores are characterized by high bending stiffness, low weight,anti-penetration and fire resistance. In addition, they can exhibit many favourable characteristics, such as high specific modulus, high specific strength and low density. Therefore, the sandwich plates with flexible cores have received increasing interests. Many researchers have investigated the response of sandwich plates with flexible cores in different loads and boundary conditions. Free vibration and buckling of laminated sandwich plates having a soft core are studied by using an efficient C0continuous finite element (FE) model based on Higher-Order Zigzag Theory (HOZT)[5]. Yang and Qiao[6]proposed a higher-order impact model for a softcore sandwich beam under impact by a foreign object and demonstrated that the core height has an important influence on the impact process of a simply supported system. Fard et al[7]developed the first-order and the higher-order impact theory to analyse the influence of multiple small impact masses on sandwich panels with transversely flexible cores and discussed the fully dynamic effects of the core layer and the face sheets. Kheirikhah et al[8]derived the equations of motion and the boundary conditions of sandwich plates with flexible cores through the minimum potential energy principle and presented an analytical solution for simply supported sandwich plates under biaxial compressive loads using Navier’s scheme. Cui and Ye et al[9]assessed the plastic deformation and energy absorption capability of sandwich plates. Shariyat et al[10]presented a quadratic finite element global-local sandwich plate with elasticity correction and demonstrated that the proposed method achieves higher accuracy than that of High-Order Zigzag Theories. In addition, the prediction of the stress at the interfaces can be complex due to the discontinuity of the mechanical properties between skins and cores.
To the best of the author’s knowledge, no accuracy evaluation of sandwich plates with flexible cores has been conducted. To address this lack of research, the present work develops a simple analytical analysis model for sandwich plate with flexible cores. The accuracy of present analysis model is very high, especially skins/core modulus ratio in 103to 105[4]. The dynamic response and resonance phenomenon of sandwich plates with a flexible core subjected to sinusoidal pulsive loading are studied. The influences of soft cores, such as skins/core thickness ratio and skins/core modulus ratio of sandwich plate, on the dynamic responses were discussed in detail. The authors of this paper look forward to providing guidance for the new type of shipbuilding sandwich structure design and application.
1 Theoretical formulation
In many sandwich plate systems, the core is designed to be light and soft relative to the skins. On the basis of the equilibrium conditions given in Eq.(1), the in-plane stress of the core is assumed to be small (in this study, assumed to be zero) and the shear stress is taken as constant over the thickness of the core[6]. The partial differential equations describing the equilibrium of the skin plies and core are as follows:

where the superscripts/subscripts c, k=t and b refer to quantities affiliated with the core, top and bottom, respectively. (u, v, w) are unknown displacement components along the (x, y, z)coordinate directions of the top, core and bottom skin plies, respectively. σxx, σyyand σzzare the components of the normal stress, and σxy, σxzand σyzare shear stresses.
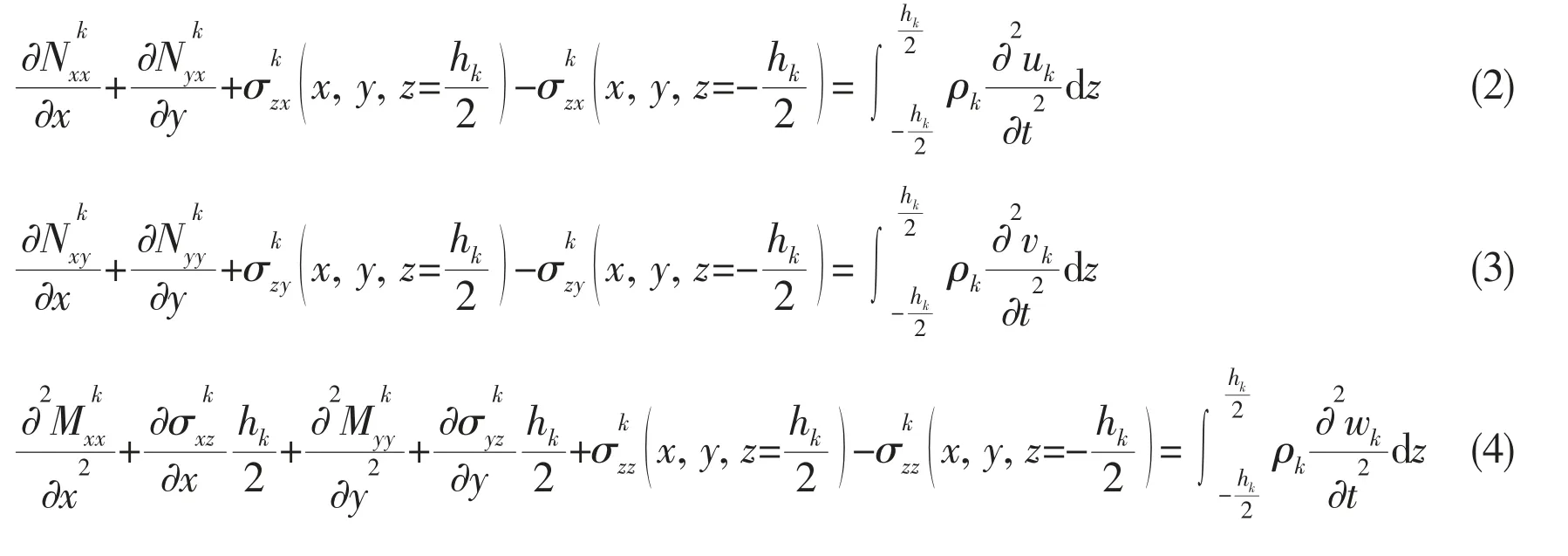
The partial differential equations describing the equilibrium of the skin plies in Eq.(1a)can be integrated as where Nxx, Nyy, Mxxand Myyare the in-plane force resultants and moment resultants, and hkis the thickness of the skin plies.
The transversely flexible core is treated as a three-dimensional elastic medium with small deformations, where the core height may change under loading, and the core cross-section does not remain planar (nonlinear displacement field in the core). By using the equilibrium condition given in Eq.(1b) and assuming that the in-plane stresses of the core are relatively small(in this study, assumed to be zero)[6]and that the shear stress is constant over the thickness of the core, the horizontal and vertical accelerations of the core can be approximated by linear interpolation[11]as

By integrating the equation of Eq.(1b) and considering that in-plane stresses do not exist in the core and the shear stresses σxzand σyzdo not change over the height, it can be obtained:


Integration of the third equation in Eq.(1b) yields

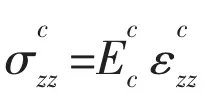

Based on the shear compatibility equation,

Integration of Eq.(12), then simplifying to get
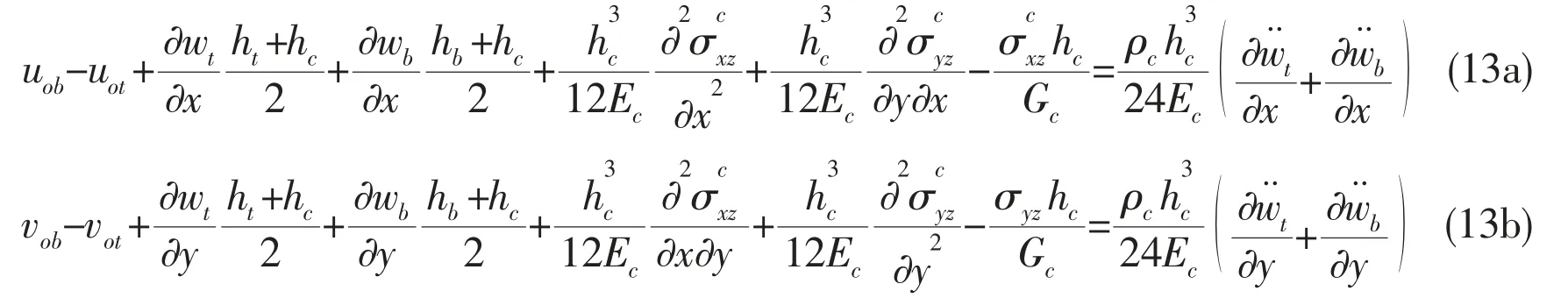
The stress resultants of the skins (including the bending-stretching coupling effects) in terms of displacement (u, v, w) as:
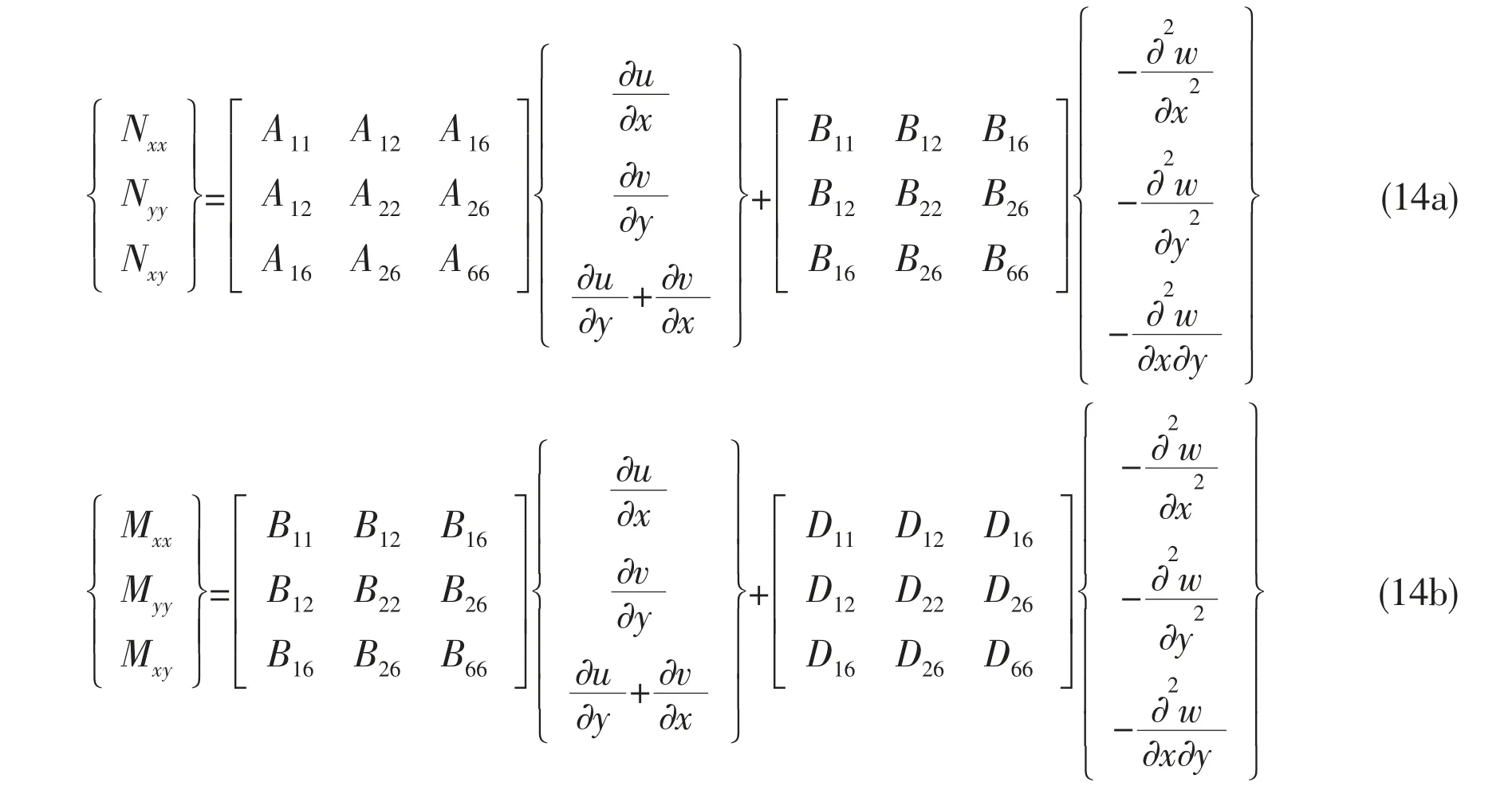
where A, B and D are the extensional, extensional-bending coupling and bending stiffness of the skin laminate, respectively.
Further, consider the stress boundary and continuity conditions of top and bottom skins as follows:
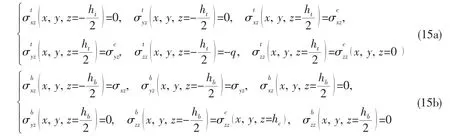
Since the top and bottom skins are composed of isotropic materials, Bij=0 (i, j=1, 2, 6),A16=A26=0 and D16=D26=0, and according to the stress resultants from Eq.(14) and the boundary conditions from Eq.(15), the governing equations Eqs.(2)-(4) and (13) can be expressed in terms of displacements and shear stresses (uot, uob, vot, vob, wt, wb, σxz, σyz) as follows:

2 Boundary conditions and analytical solutions
Consider a simply supported rectangular plate with length a and width b under transverse load q. Based on Navier approach, the following expansions of displacements and shear stress (uot, uob, vot, vob, wt, wb, σxz, σyz) are assumed as:

The transverse load q is also expanded in the double-Fourier sine series as follows:

The coefficients Qmnare given below for some typical loads:
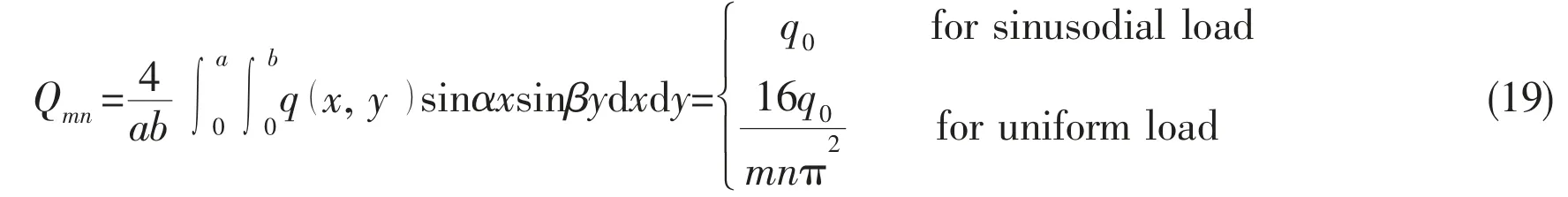
In this study, the Newmark method is used to solve dynamics equations.
3 Numerical results and discussions
3.1 Dynamic responses in different pulse loading
In this section, a sandwich plate with an isotropic flexible core is analyzed, the following material properties are considered[12]:
Et=Eb=20 GPa; Gc=40 MPa; μt= μb= μc=0.3; ρt= ρb=1 400 kg/m3; ρc=100 kg/m3; h=ht+hc+hb; hf=ht=hb; Ef=Et=Eb; a=b=2 m; ht=hb=2 mm; hc=50 mm.
The sandwich plate subjected to sinusoidal pulse load whose function as follows:

where amplitudes Q0of sinusoidal pulse are taken 10 kN, 20 kN and 30 kN, respectively, the period ω= 50π, the time t0=0.02s. The load applied to central point of simply supported rectangular sandwich plate, the load history curve are shown in Fig.1.
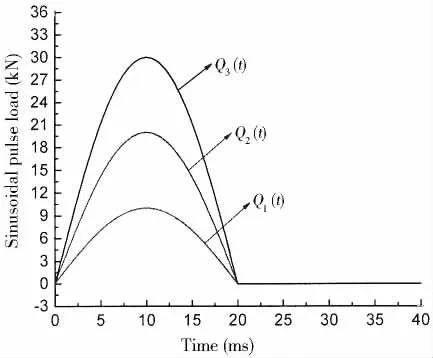
Fig.1 Assumed sinusoidal pulse loads
The displacement and velocity history curve of the sandwich plate with a flexible core in different sinusoidal pulse loads are shown in Fig.2. It can be concluded that the maximum displacements of the three different sinusoidal pulse loads are 12.58 mm, 25.17 mm and 37.71 mm, respectively, which all appear nearby 0.01 s. Due to the damping effect of the sandwich plate is not considered, so the structure will make upand-down moves in the equilibrium point when the external load is removed, the displacement amplitudes of three different loads are 5.79 mm, 14.26 mm and 22.75 mm, respectively. Compared with Fig.2a and Fig.2b, it can be found that the displacement is maximum in the loading moment, but the velocity is not, that is because the frequency of sinusoidal load is about half of the natural frequency of sandwich plate, the velocity lasts longer in +z direction than that when the frequency of sinusoidal load is close to natural frequency.
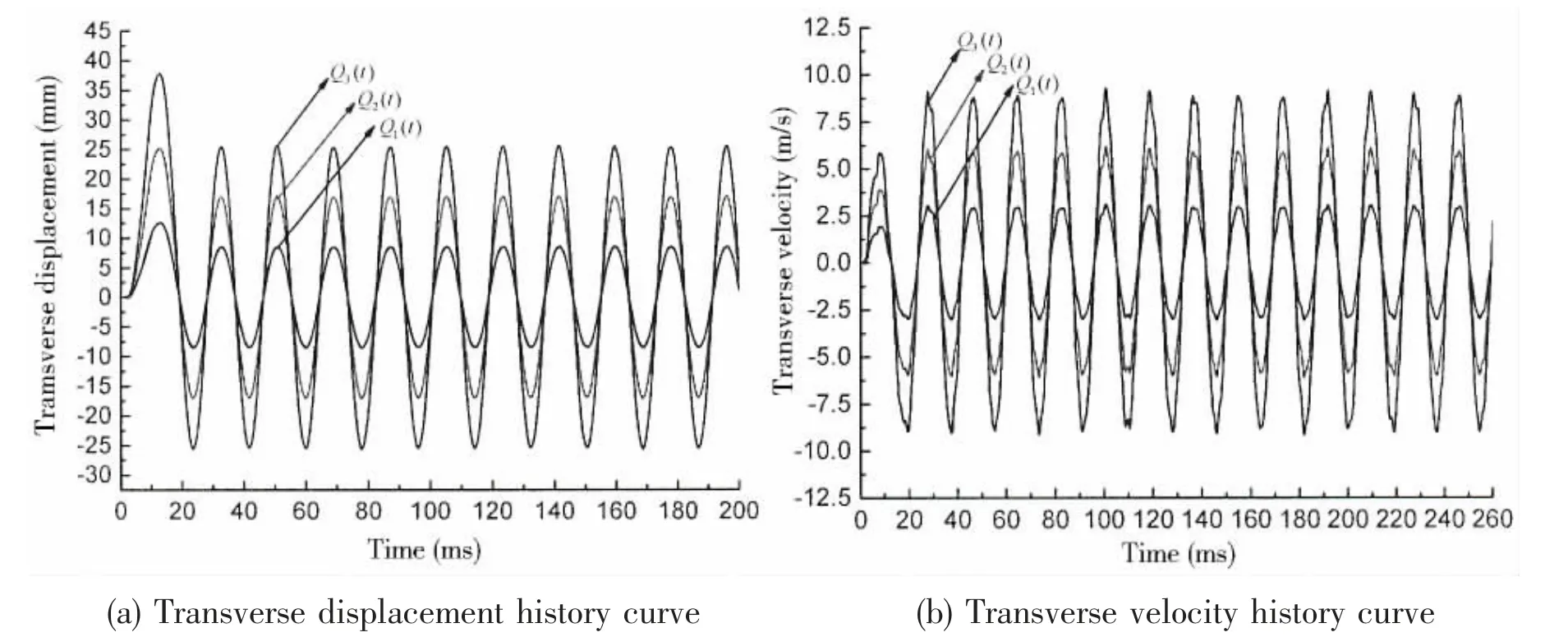
Fig.2 Comparisons of transverse displacement and velocity history curve under different sine pulse loads
The resonance will occur when the frequency of sinusoidal pulse load equals to the natural frequency of the sandwich plate, namely ω=100π, it is very dangerous if the resonance occurs. Comparisons of displacement history curve of resonance and non-resonance are shown in Fig.3, it can be concluded that the initial maximum displacement is basically the same when the sinusoidal load amplitudes are the same in resonance and non-resonance conditions, but the displacement sharply increases after the first half period under resonance. Three maximum resonance displacements are 25.76 mm, 51.44 mm and 70.28 mm which are 105.44%,104.37% and 86.37% larger than those under non-resonance conditions. The instant displacement is very large, the resonance displacement is also very large, it is extremely dangerous if the superposition of the instant and resonance displacement occurs, so the resonance must be avoided in any work condition.
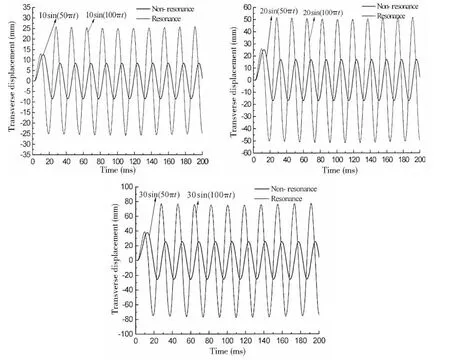
Fig.3 Resonance effect to transverse displacement of sandwich plate
As mentioned above is the dynamic response analysis for a specific sandwich plate with flexible core, the parameter study must be investigated if we want to design high specific stiffness, strength and economic sandwich plate. In the next section, the dynamic mechanics response effect of skin/core thickness ratio hc/hf(hcis core thickness, hfis skin thickness) skin/core modulus ratio Ef/Ec(Efis skin Young’s modulus, Ecis core Young’s modulus) of sandwich plates are studied.
3.2 Effect of skin/core thickness ratio
A comparative study is performed for a sandwich plate with different skin/core thickness ratios. Four different core/skin thickness ratio sandwich plates hc/hf= 1, 3, 5 and 10 (core thickness hc=0.05 m is unchanged, skin thickness is changed) are considered. The sinusoidal pulse load Q3(t )is applied in this study and the material properties are listed in above.
The displacement history curve in central point of the sandwich plate with different thickness ratios are shown in Fig.4. It can be observed that the maximum displacement of sandwich plates increases with the increase of thickness ratio, that is because the thickness ratio increases, the total thickness of sandwich plate decreases, so the stiffness of sandwich plate decreases. Synthesizes the above analysis, it can conclude that the increase proportion of displacement are proportional to the increase of thickness ratio.Compared with time interval of wave peaks,it can be found that the greater the thickness ratio of sandwich plate is, the smaller the natural frequency of sandwich plate is.
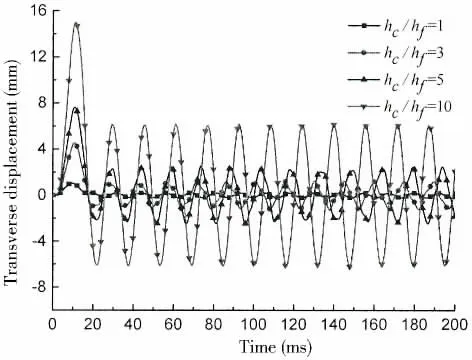
Fig.4 Time histories of displacement for varying skin thickness ratios
The transverse displacement versus the transverse velocity curves are shown in Fig.5, the value of transverse displacement and velocity value can be attained, on the basis of analyzing this curve, it is found that the transverse displacement versus the transverse velocity curves are close to elliptical shape. The major axis of sandwich plate with hc/hf=1, 3, 5 and 10 are 0.106 0 m/s, 0.488 8 m/s, 1.033 6 m/s and 2.586 9 m/s, respectively, the minor axis are 0.202 0 mm, 1.039 1 mm, 2.286 0 mm and 6.105 8 mm. There is one bulge line in every quasielliptic curve which is caused by sinusoidal pulse load, the quasi-elliptic curve is caused by free vibration of sandwich. In other words, the bulge represents load, the quasi-elliptic curve represents free vibration.
The transverse displacement difference history curve between the top and bottom skin in different thickness ratios are shown in Fig.6. It can be observed in Fig.4 and Fig.6 that the compression deformation are 3.136 4 μm, 6.466 3 μm, 7.035 5 μm and 7.215 4 μm, respectively, and the overall displacement are 1.071 9 mm, 4.526 4 mm, 7.615 7 mm and 14.889 9 mm, respectively, in hc/hf=1, 3, 5 and 10. Synthesizing the above data, it is found that the overall displacement is much bigger than the core compression deformation, the compression deformation and the overall displacement increase with the increase of thickness ratio. The core compression deformation is significant during the loading period. The elastic core compression deformation can be neglected when the applied load is removed.

Fig.5 Displacement versus velocity curves for different skin thickness ratios
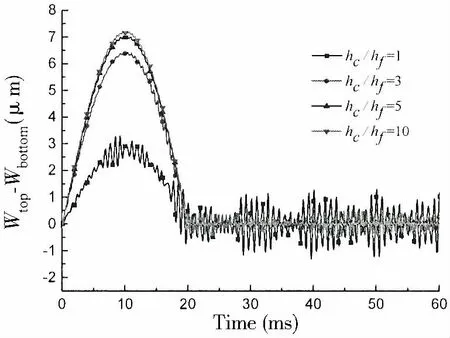
Fig.6 Time history of transverse displacements of the top and bottom skins
3.3 Effect of skin/core Young’s modulus ratio
The influence on dynamic response of core is related not only with skin/core thickness ratio, plate aspect ratio and other geometry parameters, but also with material properties. In this section, the influence on dynamic response of skin/core Young’s modulus ratio Ef/Ecis discussed. The skin/core Young’s modulus ratio Ef/Ec=103, 104, 105and 106(Ef=20 GPa and the core Young’s modulus are changed), on the other hand, the skin thickness hc=2 mm is too thin, the skin is easy to damage if the core Young’s modulus is too small, so the skin thickness hc=10 mm is chosen and the other parameters are the same with those in Section 3.1.
The central displacement history curves in different skin/core Young’s modulus ratio are shown in Fig.7. It is clearly seen that the maximum transverse displacement increases with the increase of skin/core Young’s modulus ratio. It can be deduced that the natural frequency of skin thickness hc=10 mm is smaller than skin thickness hc=2 mm and the natural vibration period increases with the increase of skin/core Young’s modulus ratio.

Fig.7 Time history of the transverse displacement for varying skin/core Young’s modulus ratio
4 Conclusions
This paper presents a new theoretical model for predicting the dynamic responses of a sandwich structure with a flexible core subjected to impact loads.In addition, a series of parametric studies were conducted with the aim to investigate the influences of some key design parameters. The following conclusions might be drawn:
(1) The new higher-order analytical model provides a more precise prediction of displacement and compression deformations of the flexible core.
(2) Under the action of an impulse load, a sandwich plate reaches its maximum displacement in a short period of time. When the pulse load is sinusoidal, the resonance will take place when the frequency of sinusoidal pulse load equals to the natural frequency of sandwich plate and the resonance is very dangerous.
(3) The increase in the displacement is proportional to the increase in the skin/core thickness ratio.
(4) The maximum transverse displacement increases with the increase in the skin/core Young’s modulus ratio.
(5) The natural vibration period increases with the increase in the skin/core Young’s modulus ratio.
- 船舶力学的其它文章
- Numerical Simulation of Flow-induced Noise of Two Circular Cylinders in Tandem and Side-by-side Arrangements Using a Viscous/ Acoustic Splitting Method
- Motions of the Floating VAWT Considering the Viscous Damping of the Spar Type Floating Foundation
- Transient Pipe Tension Influence on Dynamic Positioning Control During S-Lay Installation
- A Phase Modification Methodology in Modelling Deterministic Freak Wave Train
- Improved Moving Particle Semi-implicit Method with Large Eddy Simulation for Determining Water-entry Impact and Damage to Flat-bottomed Structures
- Numerical Simulation of Cavity and Hydrodynamic Force of the Sphere Water Entry in Consideration of Surface Wettability

